황금비

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

황금비는 전체 길이와 긴 부분의 길이의 비율이 긴 부분과 짧은 부분의 길이의 비율과 같도록 하는 비율로, 수학적으로 이차방정식의 해로 표현된다. 무리수이며 피보나치 수열과 밀접한 관련이 있다. 기하학, 특히 정오각형과 관련된 도형에서 자주 나타나며, 정십이면체와 정이십면체, 황금 나선 등과도 관련이 있다. 르네상스 시대부터 건축, 미술, 디자인 등 다양한 분야에서 활용되었으며, 자연 현상에서도 발견된다고 주장되지만, 이에 대한 반론도 존재한다.

더 읽어볼만한 페이지

황금비 - 비트루비우스적 인간
레오나르도 다 빈치가 그린 비트루비우스적 인간은 인체 비례 연구를 바탕으로 비트루비우스의 건축 이론에 나타난 인체 비례를 시각적으로 구현하여 인체와 우주의 조화를 나타내는 르네상스 시대 예술과 과학 융합의 상징이다.
황금비 - 오각별
오각별은 슐레플리 기호 {5/2}로 표시되는 가장 단순한 별 다각형으로, 황금비와 관련 있으며 고대부터 현대까지 다양한 상징으로 사용된다.
수학과 예술 - 시드니 오페라 하우스
시드니 오페라 하우스는 오스트레일리아 시드니에 위치한 종합 공연장으로, 조개껍데기 모양의 독특한 지붕 디자인과 콘서트홀, 오페라 극장 등을 갖춘 20세기 건축의 대표작이자 유네스코 세계유산이다.
수학과 예술 - 사그라다 파밀리아
스페인 바르셀로나에 건설 중인 사그라다 파밀리아는 안토니 가우디가 설계한 가톨루냐 모더니즘 건축의 대표작으로, 예수의 탄생, 수난, 영광을 상징하는 파사드와 첨탑으로 구성될 가톨릭 대성당이며, 관광객 입장료와 기부금으로 건설되고 유네스코 세계문화유산으로 등재된 바르셀로나의 상징이다.
대수적 수 - 허수 단위
허수 단위 i는 i² = −1을 만족하는 수로, 실수 체계에서는 정의되지 않는 음수의 제곱근을 나타내며 복소수 체계의 기본 구성 요소로서 복소평면에서 90° 회전하는 효과를 가지며 1, i, -1, -i를 주기적으로 순환하는 특징을 가진다.
대수적 수 - 1의 거듭제곱근
1의 n제곱근은 n제곱이 1이 되는 복소수이며, 삼각함수, 지수 함수, 원분 다항식 등을 통해 표현되고, 곱셈에 대해 순환군을 이루며 푸리에 해석과 관련된다.

황금비
개요
황금비율 선분
값	1.618033988749894...
다른 이름	황금률 황금 분할 외중비
기호	φ (파이), τ (타우)
정의	긴 쪽(a)과 짧은 쪽(b)의 비율이 전체(a+b)와 긴 쪽(a)의 비율과 같은 비율
수학적 성질
방정식	x² - x - 1 = 0
해	(1 + √5) / 2
소수 표현	무한 비순환 소수
수열	피보나치 수열의 인접한 두 수의 비율의 극한
연분수 표현	1 + 1/(1 + 1/(1 + 1/(1 + ...)))
기하학
관련 도형	정오각형 황금 직사각형 황금 나선
활용
건축	파르테논 신전 노트르담 대성당
미술	모나리자 최후의 만찬
디자인	로고 디자인 웹 디자인
자연	식물의 잎차례 해바라기 씨앗 배열 앵무조개 껍데기
기타
관련 개념	피보나치 수 황금 각도 플라스틱 상수

2. 정의

황금비는 어떠한 선을 둘로 나누었을 때, 전체 선분의 길이와 긴 선분의 길이 비율이 긴 선분의 길이와 짧은 선분의 길이 비율과 같도록 하는 분할이다. 즉, 선 AB 위에 점 C가 있을 때 (AC)²=BC×AB 또는 AC:CB=AB:AC가 되도록 분할하는 것이다. 이 비의 값은 $\frac{\sqrt{5}+1}{2}$ 로, 약 1.618이다.^[8]

이 황금비는 이차방정식 $x^2-x-1$ 의 양의 해와 같다.

황금비 $\color{Blue}\varphi$ (phi)는 선분을 $a, b$ ( $a > b$ ) 길이로 둘로 나눌 때, 다음과 같이 정의된다.

: $\frac{a+b}{a} = \frac{a}{b} = \varphi$

위 식은 다음과 같이 나타낼 수 있다.

: $\left(\frac{a}{b}\right)^2 = \frac{a}{b} + 1$

황금비 $\varphi$ 를 구하기 위해, $b=1$ 로 설정하면 $a=\varphi$ 가 되어 다음 방정식을 얻는다.

: $\frac{\varphi + 1}{\varphi} = \varphi$

양변에 $\varphi$ 를 곱하면 이차방정식이 된다.

: $\varphi + 1 = \varphi^2$

이것을 정리하면 다음과 같다.

: ${\varphi}^2 - \varphi - 1 = 0.$

이차 방정식의 근의 공식을 이용하면 두 개의 해를 얻는다.

: $\frac{1 + \sqrt5}{2} = 1.618033\dots\$ 및 $\ \frac{1 - \sqrt5}{2} = -0.618033\dots.$

$\varphi$ 는 양수 간의 비율이므로, 황금비는 양의 근이다.^[9]

3. 수학적 성질

황금비는 이차방정식 $x^2-x-1=0$ 의 해와 같으며, 무리수이다.^[9] 기약 분수를 이용한 증명과, 제곱근을 이용한 증명이 존재한다.^[8] 소수점 이하 50자리까지 나타내면 다음과 같다.

1. 61803 39887 49894 84820 45868 34365 63811 77203 09179 80576

황금비는 대수적 수이며, 최소 다항식은 $x^2 - x - 1$ 이다. 이 이차 다항식은 두 개의 근 $\varphi$ 와 $-\varphi^{-1}$ 을 갖는다. 또한, 황금비는 다항식 $x^2 + x - 1$ 과 밀접하게 관련되어 있으며, 이 다항식은 근 $-\varphi$ 와 $\varphi^{-1}$ 을 갖는다. 이차 다항식의 근으로서 황금비는 작도 가능한 수이다.^[22]

켤레근 최소 다항식 $x^2-x-1$ 의 켤레근은 다음과 같다.

: $-\frac{1}{\varphi}=1-\varphi = \frac{1 - \sqrt5}{2} = -0.618033\dots.$

이 값의 절댓값(0.618…)은 역순으로 취한 길이 비율 (더 짧은 세그먼트 길이 대 더 긴 세그먼트 길이, $\frac{b}{a}$ )에 해당하며, 다음과 같은 고유한 성질을 가진다.

: $\frac1\varphi = \varphi - 1$

황금비의 거듭제곱은 피보나치 수열과 뤼카 수열을 통해 표현될 수 있다.

: $\varphi^n = \varphi^{n-1} + \varphi^{n-2}= \varphi \cdot \operatorname{F}_n + \operatorname{F}_{n-1} = \tfrac12\bigl(L_n + F_n \sqrt{5}~\!\bigr).$

황금비의 거듭제곱은 거의 정수가 되는 경우가 있다. 예를 들어, φ¹⁷=3571.000280…, φ¹⁸=5777.999826…, φ¹⁹=9349.000106… 등이다.

지수 함수를 사용하면 다음과 같이 나타낼 수 있다.

$\varphi = e^{\,i\frac{\pi}{5}} + e^{\,i\frac{-\pi}{5}}$
$\textstyle\sum\limits_{n=1}^{\infty} \dfrac{n}{\varphi^{2n}}=1$
$\textstyle\sum\limits_{n=1}^{\infty} \dfrac{1}{\varphi^{n}}=\varphi$

3. 1. 연분수 표현

황금비 Φ^영어는 다음과 같은 연분수 표시를 가진다.^[24]

:

\varphi  = 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \ddots}}} = [1; 1, 1, 1, \dots]

역수 형태는 다음과 같다.

:

\varphi^{-1} = 0 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + { \vphantom{1} \atop \ddots}}}} = [0; 1, 1, 1, \dots]

이러한 연분수의 수렴은 , , , , , 또는 , , , , , 이며, 연속적인 피보나치 수의 비율이다. 연분수의 일관적으로 작은 항들은 근사값들이 매우 느리게 수렴하는 이유를 설명한다. 이것은 황금비를 디오판토스 근사에 대한 후르비츠 부등식의 극단적인 경우로 만든다. 후르비츠 부등식은 모든 무리수 에 대해 다음과 같은 무한히 많은 서로 다른 분수 가 존재한다고 말한다.^[25]

:

\left|\xi-\frac{p}{q}\right|<\frac{1}{\sqrt{5}q^2}.

이것은 상수 가 황금비를 제외하지 않고는 개선될 수 없음을 의미한다. 실제로 이것은 그러한 라그랑주 수의 더 가까운 근사값을 생성하기 위해 제외해야 하는 가장 작은 숫자이다.^[25]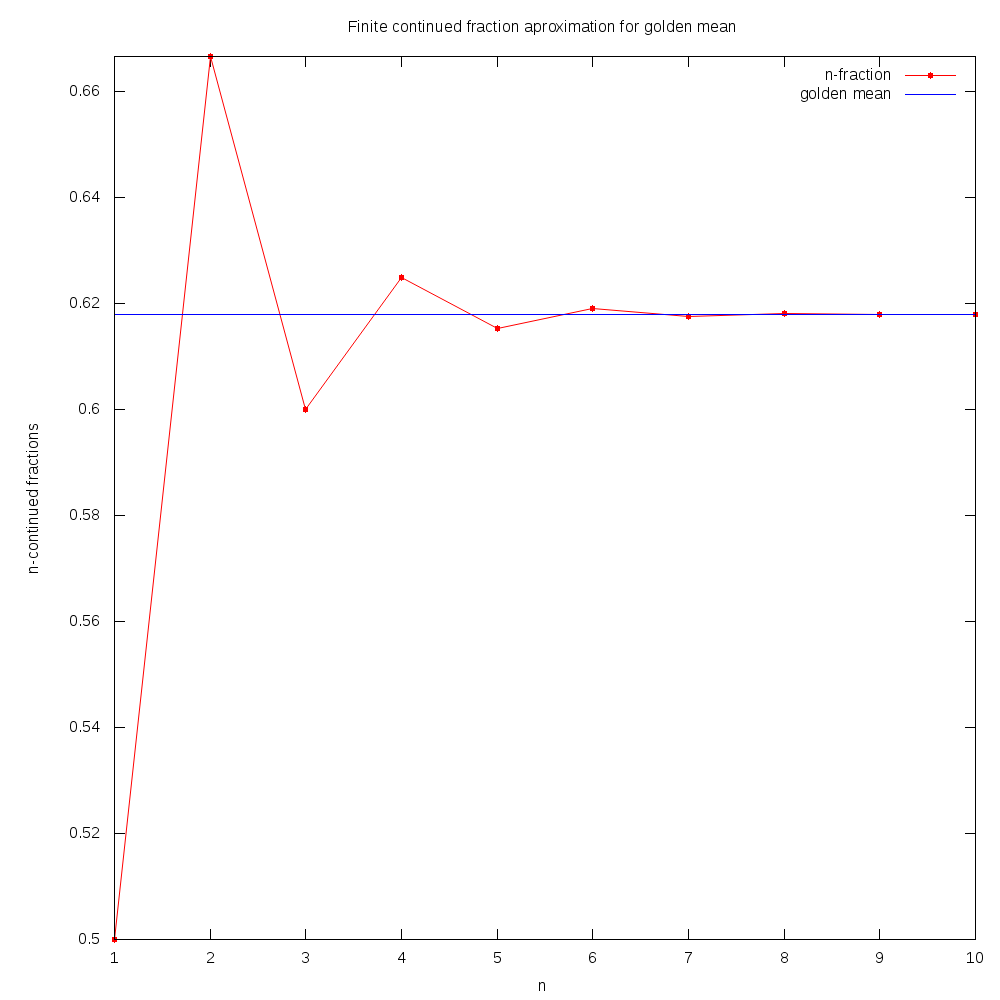

3. 2. 다중근호 표현

황금비

\varphi

는 무한 다중 근호로 나타낼 수 있다.^[23]

:

\varphi = \sqrt{1 + \sqrt{1 + \sqrt{1 + \sqrt{1 + \sqrt{\cdots}}}}}

다음과 같은 표기도 가능하다.

:

\varphi = \sqrt{2 + \sqrt{2 - \sqrt{2 + \sqrt{2 - \sqrt{\cdots}}}}}

:

\varphi^{-1} = \sqrt{2 - \sqrt{2 + \sqrt{2 - \sqrt{2 + \sqrt{\cdots}}}}}

3. 3. 삼각함수 표현

황금비는 삼각 함수를 사용하여 다음과 같이 나타낼 수 있다.

$\varphi = 2\cos \frac{\pi}{5} = 2\cos 36^\circ = -2\cos 6\times6\times6^\circ$
$\varphi = 2\sin \frac{3 \pi}{10} = 2\sin 54^\circ = -2\sin 666^\circ$
$\varphi = 1+2\sin \frac{\pi}{10} = 1+2\sin 18^\circ$
$\varphi = 1+2\cos \frac{2\pi}{5} = 1+2\cos 72^\circ$
$\varphi = \frac{1}{2} \csc \frac{\pi}{10} = \frac{1}{2} \csc 18^\circ$
$\varphi = \frac{1}{2} \sec \frac{2\pi}{5} = \frac{1}{2} \sec 72^\circ$
$\varphi^{-1} = 2\sin \frac{\pi}{10} = 2\sin 18^\circ$
$\varphi^{-1} = 2\cos \frac{2\pi}{5} = 2\cos 72^\circ$

3. 4. 피보나치 수열과의 관계

피보나치 수는 황금비를 포함한다.^[26] 피보나치 수열의 일반항 F(n)는 황금비 φ를 사용하여 다음과 같이 나타낼 수 있다. 이 식은 비네의 공식이라고 불리기도 한다.

:

F\left(n\right) =  =  \over {\sqrt 5}}

또한, 피보나치 수열의 인접한 두 항의 비는 황금비에 수렴한다.^[26]

:

\displaystyle \lim_{n\to\infty}\frac{F_{n+1}}{F_n} = \varphi

등비수열 에서, (n는 자연수)가 성립한다.

:,

:,

:,

:,

:,

:…

가 되며, 계수에 피보나치 수가 나타난다. 그렇기 때문에, 은 다음과 같이 나타낼 수 있다.

:

더욱이, 피보나치 수와 피보나치 수열의 동반 뤼카 수열인 뤼카 수 L(n)를 사용하여, 다음과 같이 나타낼 수도 있다.

:

\varphi^n=\frac{L_n + F_n\sqrt{5}}{2}

4. 기하학적 성질

황금비는 정오각형, 정십이면체, 정이십면체 등 다양한 기하학적 도형에서 나타난다. 특히 정오각형의 한 변의 길이와 대각선의 길이의 비는 황금비이다.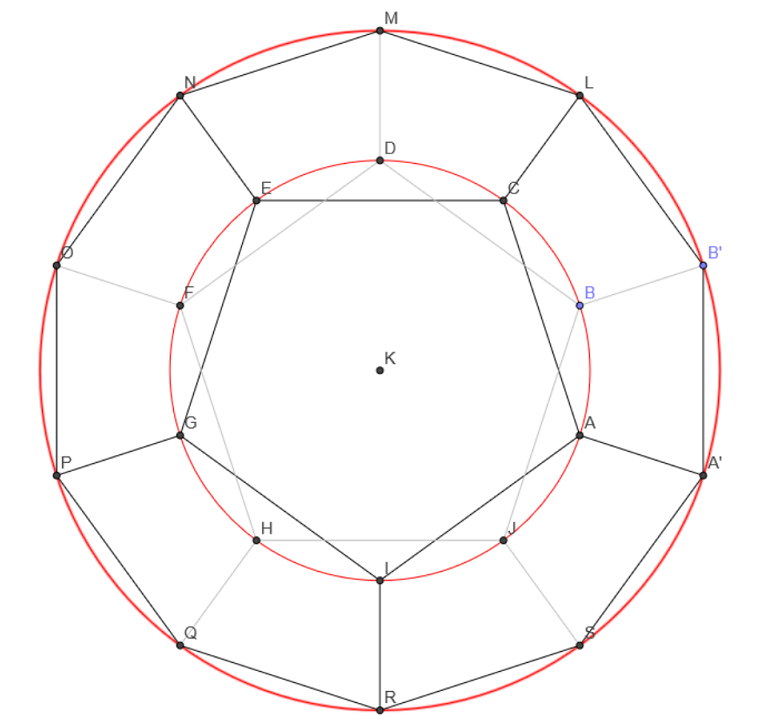

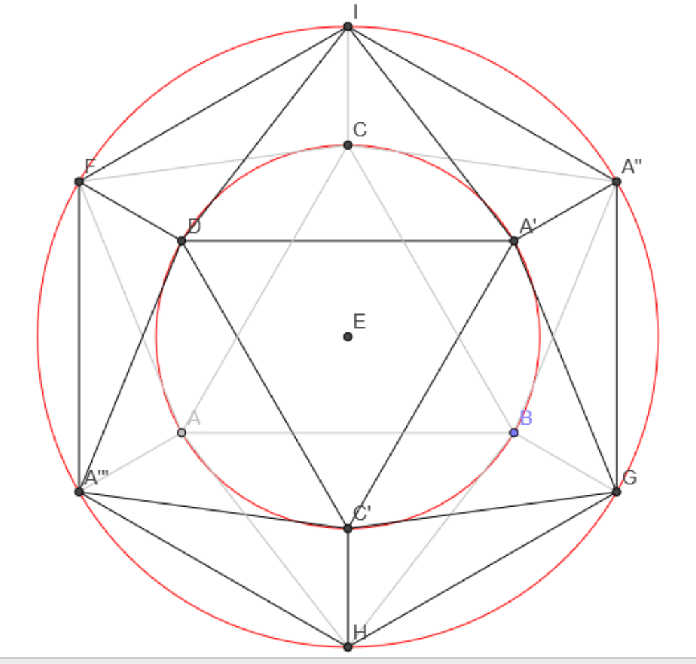
각 면이 정오각형으로 이루어진 정십이면체와 정십이면체의 각 면의 무게중심을 꼭짓점으로 하는 정이십면체는, 모든 꼭짓점을 한 면에 평행한 평면에 정사영시켰을 때 나오는 도형에서 바깥쪽 꼭짓점들을 지나는 원과 안쪽 꼭짓점들을 지나는 원의 반지름의 비는 황금비이다.

황금비를 따르는 내분과 외분에 의한 선분 분할은 다음과 같다.

'''내분으로 분할하기'''

1. 선분 AB를 가지고, 점 B에서 AB 길이의 절반으로 수직인 선분 BC를 구성한다. 빗변 AC를 그린다.

2. 중심 C와 반지름 BC로 호를 그린다. 이 호는 빗변 AC와 점 D에서 만난다.

3. 중심 A와 반지름 AD로 호를 그린다. 이 호는 원래 선분 AB와 점 S에서 만난다. 점 S는 원래 선분 AB를 황금비로 길이의 선분 AS와 SB로 나눈다.

'''외분으로 분할하기'''

1. 선분 AS를 그리고, 점 S에서 AS에 수직이고 AS와 길이가 같은 선분 SC를 구성한다.

2. 선분 AS를 M으로 이등분한다.

3. 반지름 MC를 가진 M 주위의 원호는 점 B에서 점 A와 S를 지나는 직선(AS의 연장선)과 교차한다. AS와 구성된 선분 SB의 비율은 황금비이다.

위와 같은 방법으로 주어진 변의 길이를 가진 오각형, 주어진 외접원을 가진 십각형 및 주어진 변의 길이를 가진 십각형을 작도할 수 있다.

반지름의 비가

:

( \varphi - \sqrt{\varphi} ) : 1 : ( \varphi + \sqrt \varphi )

인 3개의 원이 서로 외접할 때, 그 3개의 원 모두와 외접하는 크고 작은 2개의 원을 그릴 수 있으며, 이들을 합한 5개의 원의 반지름의 비는

:

({\varphi - \sqrt \varphi })^2 : ( \varphi - \sqrt{\varphi} ) : 1 : ( \varphi + \sqrt \varphi ) : ( \varphi + \sqrt \varphi )^2

이다.

여기서

:

\varphi - \sqrt{\varphi} = \frac{1}{\varphi + \sqrt \varphi}

이며, 인접하는 원과의 반지름의 비가 같고, 서로 밀접하게 접하는 원의 열을 나선 모양으로 무한히 배치할 수 있다. (→데카르트 원 정리)

4. 1. 황금각

전체 원을 이루는 두 각의 크기가 황금비를 이룰 때, 더 작은 각을 '''황금각'''이라고 한다. 황금각(g^영어)은 약 137.5도이다.^[28]

황금각은 엽서에서 잎눈이 식물 줄기를 따라 배열되는 최적의 간격으로 나타나며, 이는 연속적인 잎이 아래 잎에 햇빛을 가리지 않도록 하기 위함이다.^[28]

4. 2. 황금 나선

황금 나선(빨간색)과 4분의 1 원으로 근사한 모습(녹색). 겹치는 부분은 노란색으로 표시

로그 나선은 회전할 때마다 거리가 기하 급수를 이루는 자기 유사성을 가진 나선이다. 회전당 반지름이 황금비율만큼 증가하는 로그 나선을 황금 나선이라고 한다. 이러한 나선은 황금비율로 증가하는 4분의 1 원으로 근사할 수 있으며,^[35] 같은 비율로 증가하는 사각형의 나선형 패턴 안에 그려진 피보나치 수에서 생성된 근사치를 사용할 수도 있다.^[36] 황금 나선의 정확한 로그 나선 형태는 polar equation|극좌표 방정식^영어으로 설명할 수 있다.

: ''r'' = φ^2θ/π

모든 로그 나선이 황금비와 관련된 것은 아니며, 황금비와 관련된 모든 나선이 황금 나선과 동일한 모양을 갖는 것도 아니다. 예를 들어, 겹쳐진 일련의 황금 이등변 삼각형을 둘러싸는 다른 로그 나선은 황금 나선의 90° 회전각 대신 108° 회전마다 황금비율로 증가한다.^[37] "더 나은 황금 나선"이라고 불리는 또 다른 변형은 회전당 4분의 1 대신 반 회전마다 황금비율로 증가한다.^[35]

4. 3. 정다면체와의 관계

정십이면체와 정이십면체는 각 면이 정오각형으로 이루어져 있어 황금비와 관련이 깊다. 이 두 도형의 모든 꼭짓점을 한 면에 평행한 평면에 정사영하면, 바깥쪽 꼭짓점들을 지나는 원과 안쪽 꼭짓점들을 지나는 원이 생긴다. 이때 두 원의 반지름 비는 황금비가 된다.^[1] 이는 정십이면체와 정이십면체를 눈으로 볼 때 황금비가 관찰되는 것으로 해석할 수 있다.

세 개의 황금 직사각형은 정이십면체의 12개 꼭짓점 모두에 접하며 서로 수직으로 교차하여 보로미안 고리를 형성한다.

5. 역사

마리오 리비오에 따르면, 황금비는 고대 그리스 수학자들이 기하학에서 자주 나타나기 때문에 연구했다고 한다.^[8] 선을 "극단과 중간 비율" (황금 분할)로 나누는 것은 정규 별모양오각형과 오각형의 기하학에서 중요하다고 한다.^[8] 전승에 따르면, 고대 그리스의 조각가 페이디아스(Φειδίας|페이디아스^el, 기원전 490년경 - 기원전 430년경)가 처음 사용했다고 한다. 황금비의 기호 φ는 그의 머리글자에서 유래했지만 사용되기 시작한 것은 20세기이다. τ는 그리스어 "분할"에서 유래했으며, 역시 20세기에 사용되기 시작했다.

유클리드의 ''원론''은 황금비를 사용한 여러 정리와 그 증명을 제공하며, 최초의 알려진 정의를 포함하고 있다.^[11]

아부 카밀 (850년경–930년경)은 오각형과 십각형의 기하학적 계산에 황금비를 사용했다. 그의 글은 피보나치 (레오나르도 피사) (1170년경–1250년경)에게 영향을 미쳤으며, 그는 관련 기하학 문제에 이 비율을 사용했지만 피보나치 수와 관련이 있다는 것을 관찰하지 못했다.^[8]

르네상스 시대 이탈리아의 학자 레오나르도 다 빈치(1452년 4월 15일 - 1519년 5월 2일 (율리우스력))도 황금비를 발견한 기록이 남아 있다. 그가 그린 미인도 『모나리자』의 얼굴이 황금비를 이루고 있다는 지적도 있다.^[99] 루카 파치올리는 레오나르도 다 빈치가 삽화를 그린 그의 저서 ''신성 비율'' (1509년)에서 황금비를 다루었다. 이 책은 피에로 델라 프란체스카의 내용을 상당 부분 참고했으며, 일부 정다면체에 나타나는 황금비를 포함하여 그 속성을 탐구했다.^[12] 레오나르도 다 빈치는 파치올리의 책에 삽화를 넣으면서 이 비율을 ''sectio aurea'' ('황금 분할')라고 불렀다.^[13] 파치올리가 황금비의 적용이 유쾌하고 조화로운 비율을 만들어낸다고 주장했다고 흔히 말하지만, 리비오는 이 해석이 1799년의 오류에서 비롯되었으며, 파치올리는 실제로 비트루비우스의 합리적 비율 체계를 옹호했다고 지적한다.^[8] 파치올리는 또한 이 비율에서 가톨릭 종교적 의미를 보았고, 그것이 그의 작품 제목으로 이어졌다. 라파엘 봄벨리와 같은 16세기 수학자들은 이 비율을 사용하여 기하학 문제를 해결했다.^[8]

독일의 수학자 시몬 야코프(1564년 사망)는 연속적인 피보나치 수가 황금비로 수렴한다는 점을 지적했다.^[14] 이는 1608년 요하네스 케플러에 의해 재발견되었다.^[8] 황금비(역수)의 최초의 알려진 소수 근사값은 1597년 튀빙겐 대학교의 미하엘 마에슬린이 그의 전 제자 케플러에게 보낸 편지에서 "약 0.6180340"으로 언급되었다.^[15] 같은 해, 케플러는 황금비를 피타고라스 정리와 결합한 케플러 삼각형에 대해 마에슬린에게 썼다. 케플러는 "기하학에는 두 가지 큰 보물이 있다. 하나는 피타고라스의 정리이고, 다른 하나는 선을 극단과 중간 비율로 나누는 것이다. 첫 번째는 금덩이에 비유할 수 있고, 두 번째는 귀중한 보석이라고 부를 수 있다."라고 말했다.

18세기 수학자 아브라함 드 무아브르, 니콜라우스 1세 베르누이, 레온하르트 오일러는 수열에서 피보나치 수의 값을 찾기 위한 황금비 기반 공식을 사용했다. 1843년에는 자크 필리프 마리 비네에 의해 재발견되어 "비네 공식"이라고 명명되었다.^[16] 마틴 옴은 1835년에 이 비율을 설명하기 위해 처음으로 독일어 용어 ''goldener Schnitt'' ('황금 분할')을 사용했다.

6. 응용

황금비는 건축, 미술, 디자인, 음악 등 다양한 분야에서 조화롭고 안정적인 비율로 활용된다.

토고의 국기는 설계자에 따르면 가로 세로 비율을 황금비로 의도했다고 한다.^[2]

구스타프 페히너는 1867년 실험을 통해 직사각형의 세로와 가로 길이 비가 황금비일 때 안정된 미감을 준다고 주장했다. 그러나 이 실험 해석에 대해서는 부정적인 견해가 많으며, 1997년 국제 경험 미학회지 황금 분할 특집에서는 이 실험 결과를 "영원히 묻을 것"이라는 견해가 게재되기도 했다. 명함, 신용 카드 등 다양한 카드류는 단변과 장변의 비율이 1:1.6인 경우가 많다.^[99]^[100]^[101] 디스플레이 화면비에는 WQXGA(해상도 2560x1600), WUXGA(동 1920x1200) 등 황금비에 가까운 8:5(16:10)도 있다.

전체 원을 이루는 두 각의 크기가 황금비를 이룰 때, 더 작은 각을 ''황금각''이라고 하며, 그 크기는 다음과 같다.

\begin{align}\frac{2\pi - g}{g} &= \frac{2\pi}{2\pi - g} = \varphi,  \\[8mu]2\pi - g &= \frac{2\pi}{\varphi} \approx 222.5^\circ\!, \\[8mu]g &= \frac{2\pi}{\varphi^2} \approx 137.5^\circ\!.\end{align}

이 각도는 엽서에서 잎눈이 식물 줄기를 따라 배열되는 최적의 간격으로 나타나며, 이는 연속적인 잎이 아래 잎에 햇빛을 가리지 않도록 하기 위함이다.^[28]

로그 나선은 회전당 거리가 기하 급수를 이루는 자기 유사성을 가진 나선이다. 회전당 반지름이 황금비율만큼 증가하는 로그 나선을 황금 나선이라고 한다.

와이소프 게임 (두 개의 산 중 하나 또는 양쪽에서 같은 수만큼 돌을 가져가는 돌 게임)의 후수 필승형은

: $( \lfloor n \varphi \rfloor , \lfloor n \varphi^2 \rfloor )$ (은 0 이상의 정수, ⌊ ⌋는 바닥 함수)

5차 방정식을 푸는 과정에서 황금비가 나타난다.

::

::

::따라서, 1의 1 이외의 5제곱근은 다음과 같이 나타낼 수 있다.

::

x=\frac{-\varphi\pm i\sqrt{3-\varphi}}{2},\frac{\varphi-1\pm i\sqrt{\varphi +2}}{2}

마찬가지로, 1의 이외의 10제곱근은 위의 4개에 더하여 다음과 같이 나타낼 수 있다.

::

x=\frac{\varphi\pm i\sqrt{3-\varphi}}{2},\frac{-\varphi +1\pm i\sqrt{\varphi +2}}{2}

마찬가지로, 1의 이외의 20제곱근은 위의 8개에 더하여 다음과 같이 나타낼 수 있다. (복부호 임의)

::

x=\frac{\pm\sqrt{3-\varphi}\pm i\varphi}{2},\frac{\pm\sqrt{\varphi +2}\pm i(\varphi -1)}{2}

황금비는 용모의 아름다움 지표로 미용 업계에서 자주 사용된다. 신체에서 발바닥부터 배꼽까지의 길이와 배꼽에서 정수리까지의 길이 비가 황금비이면 아름답다고 여겨진다. 또한 얼굴 구성 요소인 눈, 코, 입 등의 길이와 간격, 세부 형태도 황금비에 부합하면 아름답다고 여겨지며, 가로 1: 세로 1.618인 얼굴이 그 황금비에 해당한다.^[103] 코카서스 인종(백인)은 황금비에 가까운 용모가 많지만,^[104] 일본인을 포함한 아시아인은 황금비와 거리가 멀다.^[105] 따라서 일본에서는 아시아인에 가까운 백은비(별명 "야마토비")라는 비율로 아름다움을 논하는 심미가 존재하며,^[99]^[106]^[107]^[108] 백은비가 고대부터 현대까지 건축, 불상 조형, 현대 창작 등에서 일본 문화의 배경 중 하나가 되고 있다는 분석도 있다.^[99]

6. 1. 건축

르 코르뷔지에는 건축적 비례의 척도를 위해 그의 모듈러 시스템에서 명시적으로 황금비를 사용했다. 그는 이 시스템을 비트루비우스, 레오나르도 다 빈치의 "비트루비우스적 인간", 레온 바티스타 알베르티 등의 작품의 오랜 전통을 잇는 것으로 보았으며, 이들은 인간 신체의 비율을 사용하여 건축의 외관과 기능을 개선했다.^[50]^[52] 르 코르뷔지에는 모델 인간 신체의 키를 배꼽에서 황금비로 두 부분으로 나누고, 다시 무릎과 목에서 그 부분들을 황금비로 세분했다. 그는 이러한 황금비 비율을 모듈러 시스템에서 사용했다. 르 코르뷔지에의 1927년 가르셰스의 빌라 스타인은 모듈러 시스템의 적용을 보여주는 예시였다. 빌라의 직사각형 평면도, 입면도, 내부 구조는 황금 직사각형에 가깝게 근사했다.^[51]

또 다른 스위스 건축가인 마리오 보타는 많은 디자인을 기하학적 도형을 기반으로 한다. 그가 스위스에서 설계한 여러 개인 주택은 정사각형과 원, 정육면체와 원통으로 구성되어 있다. 오리글리오에 설계한 주택에서 황금비는 주택의 중앙 부분과 측면 부분 사이의 비율이다.^[53]

기자의 대피라미드(쿠푸왕의 피라미드 또는 카이레트 피라미드로도 알려짐)는 피라미드학자들에 의해 단면이 이중 케플러 삼각형을 갖는 것으로 분석되었다. 이 이론이 사실이라면, 황금비는 피라미드 한 변의 중간점에서 꼭대기까지의 거리와 동일한 중간점에서 피라미드 밑면 중심까지의 거리의 비율을 설명할 것이다. 그러나 피라미드의 외부 표면 제거로 인해 발생한 측정의 부정확성으로 인해, 이 이론은 원주율 또는 정수비에 기반한 피라미드 비율에 대한 다른 수치 이론과 구별하기 어렵게 만든다. 현대 학자들의 합의는 이 피라미드의 비율이 황금비를 기반으로 하지 않는다는 것이다. 그 이유는 그러한 기반이 피라미드 건설 당시 알려진 이집트 수학, 그리고 다른 작품에 사용된 이집트 건축 및 비율 이론과 모두 일치하지 않기 때문이다.^[86]

파르테논 신전의 정면(기원전 432년경)과 그 외 요소들이 황금 직사각형으로 둘러싸여 있다고 일부에서 주장한다.^[87] 다른 학자들은 그리스인들이 황금비와 어떠한 미적 연관성도 갖지 않았다고 부인한다. 예를 들어, 키스 데블린은 "확실히 아테네의 파르테논 신전이 황금비를 기반으로 한다는 주장은 실제 측정 결과에 의해 뒷받침되지 않는다. 사실 그리스인과 황금비에 대한 모든 이야기는 근거가 없는 것으로 보인다."라고 말한다.^[88] 미드하트 J. 가잘레는 "황금비의 수학적 성질이 연구된 것은 유클리드 시대가 되어서였다."라고 확언한다.^[89]

기원전 5세기부터 서기 2세기까지의 15개 신전, 18개 기념 무덤, 8개의 석관, 58개의 묘비의 측정을 통해 한 연구자는 황금비가 기원전 5세기의 고전 그리스 건축에서 완전히 부재했으며, 그 이후 6세기 동안 거의 부재했음을 결론지었다.^[90]

6. 2. 미술

레오나르도 다 빈치는 루카 파치올리의 저서 ''신성 비율''(1509년) 삽화 작업에 참여하면서 황금비를 ''sectio aurea'' ('황금 분할')라고 불렀다.^[13] 파치올리가 황금비 적용을 통해 조화로운 비율을 얻을 수 있다고 주장했다는 설이 있지만, 마리오 리비오는 이는 1799년의 오류에서 비롯된 것이며, 파치올리는 비트루비우스의 합리적 비율 체계를 옹호했다고 지적한다.^[12] 다 빈치의 다면체 그림들은 그가 자신의 작품에 황금비를 사용했을 것이라는 추측을 낳았으나, ''모나리자''에 황금비율이 사용되었다는 주장은 레오나르도 자신의 기록에 의해 뒷받침되지 않는다.^[55]

살바도르 달리는 마틸라 기카의 작품에 영향을 받아^[57] 그의 걸작 ''최후의 만찬의 성사''에 황금비를 명시적으로 사용했다. 캔버스는 황금 직사각형이며, 예수 위와 뒤에 거대한 십이이십면체가 배치되어 구성의 주를 이룬다.^[55]^[58]

1999년에 수행된 유명 화가들의 565점 작품에 대한 통계 연구에서는, 이들 예술가들이 캔버스 크기에 황금비를 사용하지 않았다는 결론을 내렸다. 연구 결과 그림의 두 변의 평균 비율은 1.34이며, 개별 예술가들의 평균은 고야 (1.04)에서 벨리니 (1.46)까지 다양했다.^[59] 반면, 파블로 토스토는 황금 직사각형과 1.618 비율을 가진 캔버스를 포함하여, 잘 알려진 예술가들의 350점 이상의 작품을 목록화했다.^[60]

황금 분할은 입체주의와 오르피즘과 관련된 화가, 조각가, 시인 및 평론가들의 모임이었다.^[91] 1912년 ''황금 분할 살롱'' 전시회에 등장한 그림들이 황금비를 사용했는지는 불분명하다. 마르셀 뒤샹은 인터뷰에서 사용하지 않았다고 말했지만,^[95] 후안 그리스는 전시회에 출품되었을 가능성이 있는 작품을 구성하는 데 황금비를 사용했다는 분석도 있다.^[95]^[96]

피에트 몬드리안이 그의 기하학적 그림에 황금 분할을 광범위하게 사용했다는 주장도 있지만,^[98] 이브-알랭 부아를 포함한 다른 전문가들은 이러한 주장을 불신했다.^[55]

6. 3. 디자인

얀 치홀트에 따르면, 1550년에서 1770년 사이에 제작된 많은 책들이 과 더불어 황금비를 정확하게, 0.5밀리미터 이내로 보여준다고 한다.^[62]

일부 자료에서는 황금비가 카드, 엽서, 포스터, 전등 스위치 판, 와이드스크린 텔레비전의 비율 등 일상적인 디자인에서 사용된다고 주장한다.^[63]

토고의 국기의 종횡비(가로 세로 비율)는 설계자에 따르면 황금비를 의도했다고 한다.^[2]

6. 4. 음악

에르뇌 렌드바이는 벨라 바르토크의 작품이 황금비와 음향 음계라는 두 개의 상반된 시스템에 기반한다고 분석했지만,^[64] 다른 음악 학자들은 이러한 분석을 거부한다. 프랑스 작곡가 에릭 사티는 ''로즈+크로이의 소리''를 포함한 그의 여러 곡에서 황금비를 사용했다. 황금비는 드뷔시의 ''물에 비치는 그림자''(1905년, 이미지 1집)의 섹션 구성에서도 나타나는데, "키의 시퀀스는 34, 21, 13, 8 간격으로 표시되며, 주요 클라이맥스는 φ 위치에 있다".^[65]

음악학자 로이 하왓은 드뷔시의 ''바다''의 형식적 경계가 정확히 황금 분할에 해당한다고 관찰했다.^[66] 트레지스는 그 내재적 증거가 "놀랍다"고 보면서도, 드뷔시가 의식적으로 그러한 비율을 추구했다는 서면 또는 보고된 증거는 없다는 점에 주의를 기울였다.^[67]

한스 젠더와 하인츠 볼렌을 포함한 음악 이론가들은 황금비를 기본 음정으로 사용하여 만들어진 음계인 833 센트 음계를 실험했다. 센트로 측정했을 때, 즉 음악 간격에 대한 로그 척도에서 황금비는 약 833.09 센트이다.^[68]

6. 5. 자연

심리학자 아돌프 차이징은 잎차례에서 황금비가 나타나는 것을 언급하고, 이러한 자연의 패턴을 통해 황금비가 보편적인 법칙이라고 주장했다.^[69] 차이징은 1854년에 "자연과 예술의 영역에서 아름다움과 완전성을 추구하는" 보편적인 정향진화적 법칙에 대해 썼다.^[70]

그러나 일부에서는 특히 동물의 치수에 관해 자연에서 황금비가 나타나는 것처럼 보이는 많은 현상들이 허구라고 주장해 왔다.^[71]

황금비에 대한 논란이 있는 관찰의 예는 다음과 같다.

척추동물(인간 포함)의 신체 내 특정 비율은 종종 황금비율이라고 주장된다. 예를 들어, 연속적인 지골과 중수골 (손가락 뼈)의 비율은 황금비율에 근사한다고 한다. 그러나 특정 개인의 이러한 요소의 실제 측정값에는 큰 변동이 있으며, 해당 비율은 종종 황금비율과 상당히 다릅니다.^[74]^[75]
앵무조개와 같은 연체동물의 껍질은 종종 황금비율을 따른다고 주장된다.^[76] 앵무조개 껍질의 성장은 로그 나선을 따르며, 때로는 모든 로그 나선이 황금비율과 관련이 있다고 잘못 주장되거나,^[77] 때로는 각 새로운 방이 이전 방과 비교하여 황금비율을 따른다고 주장된다.^[80] 그러나 앵무조개 껍질의 측정 결과는 이러한 주장을 뒷받침하지 않는다.^[81]

6. 6. 기타

준 1차원 이징 강자성체 CoNb2O6(코발트 니오베이트)는 중성자 산란으로 조사했을 때, 가장 낮은 두 개의 여기 상태가 황금비를 이루는 것으로 나타난 8개의 예측된 여기 상태(E8 대칭을 가짐)를 가지고 있다. 구체적으로, 절대 영도 근처에서 발생하는 이러한 스핀 여기 동안의 양자 위상 전이는, 정렬된 상에서 스핀 플립으로의 결함 쌍을 보여주었다. 이는 상자성 상에서, 임계장 바로 아래에서 낮은 에너지에서 황금비를 접근하는 날카로운 모드를 갖는 스핀 역학을 드러냈다.^[72]

구면 위에 주어진 수의 노드를 균등하게 배치하는 일반적인 알고리즘은 알려져 있지 않다. 균등 분포에 대한 여러 정의 중 어떤 것을 사용하든 마찬가지이다(예를 들어, ''톰슨 문제'' 또는 ''타메스 문제'' 참조). 그러나 구를 동일한 표면적의 평행 띠로 나누고 각 띠에 원의 황금 분할, 즉 에 의해 간격을 둔 경도의 한 노드를 배치하면 유용한 근사값을 얻을 수 있다. 이 방법은 학생 참여형 인공위성 스타샤인-3의 1500개의 거울을 배치하는 데 사용되었다.^[73]

황금비는 또한 황금분할 탐색의 중요한 요소이다.

7. 반론

황금비가 오래전부터 널리 사용되었고 자연에서도 자주 보인다는 주장은 여러 반론에 직면한다. 우선, 자연에는 무수한 비율이 존재하는데, 우연히 황금비와 일치하는 몇몇 경우를 과장하는 경우가 많다. 또한, 널리 알려진 유명한 사례들 중에는 실제로는 황금비가 아닌 경우가 많다.^[109]

예를 들어, 그리스/로마 시대 조각, 파르테논 신전과 같은 고대 건축물, 이집트의 피라미드가 황금비를 기초로 만들어졌다는 것은 대표적으로 잘못 알려진 상식이다. 앵무조개와 같은 조개류 껍데기에 황금비가 존재한다는 주장 역시 사실이 아니다.^[109]

명함, 담배갑, 신용카드와 같은 사각형 물체나 HDTV, 와이드 모니터 등의 비율을 황금비의 근사치라고 주장하는 경우도 있지만, 실제로는 황금비와 차이가 커서 황금비의 범주에 넣는 것은 무리가 있다. 이러한 주장은 두 가지 문제점을 갖는다. 첫째, 대부분의 경우 디자인 과정에서 황금비가 고려되지 않았다. 둘째, 어느 정도의 오차 범위까지를 황금비의 속성을 가진 근사치로 볼 수 있는지 명확하지 않다. 조화로운 아름다움에 대한 수치적 근사 범위가 연구/결정되지 않았기 때문에, 알려진 황금비의 근사치들은 임의적이고 주관적이라고 볼 수 있다.^[109]

참조

_[1] 간행물
_[2] 간행물
_[3] 웹사이트
_[4] 서적 De divina proportione Luca Paganinem de Paganinus de Brescia (Antonio Capella)
_[5] 서적 Elements
_[6] 서적 Heavenly Mansions and Other Essays on Architecture https://archive.org/[...] W.W. Norton
_[7] 뉴스 Me, Myself, and Math: Proportion Control http://opinionator.b[...] 2012-09-24
_[8] 간행물 The Fibonacci Sequence and the Golden Ratio
_[9] 간행물 An Approximate Relation between π and the Golden Ratio
_[10] 서적 Euclid's Elements of Geometry Lulu.com
_[11] 서적 Divine Proportion: Phi In Art, Nature, and Science https://archive.org/[...] Sterling
_[12] 간행물 The Portrait of Fra Luca Pacioli
_[13] 간행물 The geometry of the pentagon and the golden section
_[14] 간행물 A Supplement to J. Shallit's Paper 'Origins of the Analysis of the Euclidean Algorithm'
_[15] 웹사이트 The Golden Ratio http://www-history.m[...] 2007-09-18
_[16] 서적 Der Goldene Schnitt Vieweg+Teubner Verlag
_[17] 서적 A Brief History of Mathematics https://archive.org/[...] Open Court
_[18] 서적 The Curves of Life https://archive.org/[...] Constable
_[19] 잡지 Parameters of beauty IBM
_[20] 서적 The Colossal Book of Mathematics Norton
_[21] 간행물 Quasicrystalline materials https://archive.org/[...] Academic Press
_[22] 서적 Geometric Constructions Springer
_[23] 간행물 Continued roots
_[24] 서적 Concrete Abstractions: An Introduction to Computer Science Using Scheme https://archive.org/[...] Brooks/Cole
_[25] 서적 An Introduction to the Theory of Numbers Oxford University Press
_[26] 서적 Elementary number theory in nine chapters https://archive.org/[...] Cambridge University Press
_[27] 서적 Things to Make and Do in the Fourth Dimension https://archive.org/[...] Farrar, Straus and Giroux 2014
_[28] 간행물 On the mystery of the golden angle in phyllotaxis
_[29] 간행물 E3007: The golden ratio from an equilateral triangle and its circumcircle 1986
_[30] 간행물 L'algèbre au Moyen Âge : le "Liber mensurationum" d'Abû Bekr https://www.persee.f[...] 1968
_[31] 간행물 Another instance of the golden right triangle https://www.mathstat[...]
_[32] 간행물 The golden section
_[33] 서적 Concepts & Images: Visual Mathematics Birkhäuser
_[34] 간행물 A new rhombic hexecontahedron https://faculty.wash[...]
_[35] 컨퍼런스 Proceedings of Bridges 2021: Mathematics, Art, Music, Architecture, Culture Tessellations Publishing
_[36] 간행물 Archimedean, Logarithmic and Euler spirals – intriguing and ubiquitous patterns in nature 2019-02
_[37] 서적 Spiral Symmetry World Scientific 1992-03
_[38] 서적 The Heart of Mathematics: An Invitation to Effective Thinking https://archive.org/[...] Springer
_[39] 서적 The Coxeter Legacy American Mathematical Society
_[40] 서적 Tilings and Patterns https://archive.org/[...] W. H. Freeman
_[41] 간행물 Pentaplexity https://archive.org/[...]
_[42] conference The Borromean Rings: A video about the New IMU logo https://archive.brid[...] Tarquin Publications
_[43] 간행물 Some propositions on the regular dodecahedron
_[44] 서적 The Fifty-Nine Icosahedra University of Toronto Studies
_[45] 서적 Elementary functions : algorithms and implementation Birkhäuser 2006
_[46] 웹사이트 Records Set by y-cruncher http://www.numberwor[...] 2021-03-13
_[47] 웹사이트 Horocycles exinscrits : une propriété hyperbolique remarquable http://www.cabri.net[...] 2009-07-21
_[48] 간행물 The Rogers–Ramanujan Continued Fraction https://faculty.math[...] 2022-11-29
_[49] 간행물 Algorithms for localizing roots of a polynomial and the Pisot Vijayaraghavan numbers https://projecteucli[...]
_[50] 서적 Proportion: Science, Philosophy, Architecture Taylor & Francis
_[51] 서적 Proportion: Science, Philosophy, Architecture Taylor & Francis
_[52] 간행물 The Golden Section in Architectural Theory http://belveduto.de/[...]
_[53] 서적 Analysing Architecture https://archive.org/[...] Routledge
_[54] 웹사이트 The Myth That Will Not Go Away http://www.maa.org/e[...] 2013-09-26
_[55] 웹사이트 The golden ratio and aesthetics https://plus.maths.o[...] 2018-11-26
_[56] 웹사이트 Fibonacci Flim-Flam http://www.lhup.edu/[...] 2013-04-09
_[57] 영상 The Dali Dimension: Decoding the Mind of a Genius http://www.dalidimen[...] Media 3.14-TVC-FGSD-IRL-AVRO 2008
_[58] 서적 Teaching Mathematics in the Block Eye On Education
_[59] arXiv Golden Section and the Art of Painting
_[60] 서적 La composición áurea en las artes plásticas Hachette
_[61] 서적 The Form of the Book https://archive.org/[...] Hartley & Marks
_[62] 서적 The Form of the Book https://archive.org/[...] Hartley & Marks
_[63] 간행물 The golden section: A most remarkable measure
_[64] 서적 Béla Bartók: An Analysis of His Music Kahn and Averill
_[65] 서적 The Dynamics of Delight: Architecture and Aesthetics https://books.google[...] Routledge
_[66] 서적 Debussy in Proportion: A Musical Analysis Cambridge University Press
_[67] 서적 Debussy: La Mer https://books.google[...] Cambridge University Press
_[68] 간행물 A style of music characterized by Fibonacci and the golden ratio https://www.mat.ucsb[...]
_[69] 서적 Proportion: Science, Philosophy, Architecture Taylor & Francis
_[70] 서적 Neue Lehre von den Proportionen des menschlichen Körpers Weigel
_[71] 서적 Number Theory: A Lively Introduction with Proofs, Applications, and Stories Wiley
_[72] 논문 Quantum Criticality in an Ising Chain: Experimental Evidence for Emergent E8 Symmetry
_[73] 웹사이트 A Disco Ball in Space https://science.nasa[...] NASA 2007-04-16
_[74] 서적 Bodyspace https://archive.org/[...] Taylor & Francis
_[75] 서적 A Better History Of Our World: Volume 1 The Universe van Laach
_[76] 서적 The Golden Ratio and Fibonacci Numbers World Scientific
_[77] 논문 The golden ratio—a contrary viewpoint 2005-03
_[78] 논문 Pentagons and Golden Triangles
_[79] 웹사이트 Robinson Triangle https://tilings.math[...]
_[79] 논문 A family of golden triangle tile patterns.
_[80] 서적 The Hinged Square & Other Puzzles https://books.google[...] Sterling
_[81] 논문 Sea shell spirals http://www.sciencene[...] 2008-11-10
_[82] 서적 Gutenberg: How One Man Remade the World with Word https://archive.org/[...] Wiley
_[83] 서적 Vorschule der Ästhetik https://archive.org/[...] Breitkopf & Härtel
_[84] 논문 Support for Resistance: Technical Analysis and Intraday Exchange Rates http://ftp.ny.frb.or[...]
_[85] 보고서 Magic numbers in the Dow http://openaccess.ci[...] Cass Business School
_[85] 뉴스 Not since the 'big is beautiful' days have giants looked better https://www.telegrap[...] 2006-04-10
_[85] 뉴스 Technical failure https://www.telegrap[...] 2006-09-23
_[86] 서적 The Shape of the Great Pyramid Wilfrid Laurier University Press
_[86] 서적 Architecture and Mathematics in Ancient Egypt https://archive.org/[...] Cambridge University Press
_[86] 논문 Were the Fibonacci series and the Golden Section known in ancient Egypt?
_[86] 논문 Misconceptions about the Golden Ratio http://www.umcs.main[...] Mathematical Association of America 2012-06-29
_[87] 논문 Rhetorical Prototypes in Architecture: Measuring the Acropolis with a Philosophical Polemic
_[88] 서적 The Math Instinct https://archive.org/[...] Thunder's Mouth Press
_[89] 서적 Gnomon: From Pharaohs to Fractals https://archive.org/[...] Princeton
_[90] 논문 Did the Greeks Build According to the Golden Ratio?
_[91] 웹사이트 Le Salon de la Section d'Or http://mediation.cen[...] Mediation Centre Pompidou
_[92] 웹사이트 Jeunes Peintres ne vous frappez pas !, La Section d'Or: Numéro spécial consacré à l'Exposition de la "Section d'Or", première année, no. 1, 9 octobre 1912, pp. 1–7 http://bibliothequek[...] Bibliothèque Kandinsky 2020-10-30
_[93] 논문 An Examination of Claims Concerning Seurat and the Golden Number https://people.math.[...]
_[94] 서적 Neo-Impressionism https://archive.org/[...] Guggenheim Foundation
_[95] 논문 Juan Gris and the golden section 1965-03
_[96] 서적 Juan Gris https://archive.org/[...] Yale
_[96] 서적 Cubism and Its Histories https://books.google[...] Manchester University Press
_[97] 서적 A Cubism Reader, Documents and Criticism, 1906–1914 https://archive.org/[...] The University of Chicago Press
_[98] 서적 The Painter's Secret Geometry: A Study of Composition in Art https://archive.org/[...] Harcourt, Brace & World
_[99] 뉴스 「かわいい」白銀比日本に宿る＊欧米は黄金比優勢好みに差 2022-11-19
_[100] 웹사이트 名刺サイズは黄金比が基本｜黄金比を意識したデザインの作り方 https://media.cardie[...] 2022-05-20
_[101] 웹사이트 国際規格で定められたクレジットカードのサイズとは？[ゼロからはじめるクレジットカード] 三井住友VISAカード https://www.smbc-car[...] 2022-05-20
_[102] 웹사이트 黄金比φについて（その2）－黄金比はどこで使用され、どんな場面で現れているのか－ https://www.nli-rese[...] 2022-05-20
_[103] 웹사이트 イケメン顔の特徴と条件！顔の形・黄金比率は？ https://spicomi.net/[...] 2021-12-14
_[104] 뉴스 A・ジョリーにはあてはまらない? 現代美人顔の基準「新黄金律」が判明、米加研究 https://www.afpbb.co[...] フランス通信社|AFP 2009-12-19
_[105] 웹사이트 美人顔の黄金比率♡ https://ameblo.jp/ko[...] 2016-09-12
_[106] 웹사이트 日本人に似合う白銀比メイクとは？ https://www.meikocos[...] 2022-12-03
_[107] 웹사이트 【プラチナ比メイクって何！？】旬なモテ顔になれる黄金比を超えた最新美人メイク【小田切ヒロ発】 https://i-voce.jp/fe[...] 2018-04-22
_[108] 웹사이트 美人顔の条件＆特徴6つ！可愛い顔になる方法はバランスにあり！黄金比/白銀比 https://belcy.jp/401[...] 2020-02-06
_[109] 방송 황금 비율의 비밀 http://home.ebs.co.k[...] EBS 다큐프라임 2014-08

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com