맨위로가기

다수결 함수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

다수결 함수는 입력의 50% 이상이 참일 때 참을 반환하는 논리 게이트이다. 부울 회로 및 회로 복잡도 분야에서 사용되며, 전가산기, 3중 모듈 중복성 시스템의 오류 수정 등에 활용된다. 회로 복잡도 이론에 따르면 AC0 회로에서 서브 지수 크기로 계산할 수 없으며, 3진 다수결 함수는 특정 성질을 만족한다. 다수결 함수는 일반화될 수 있으며, 동률 발생 시 0으로 편향되거나 무작위로 해소될 수 있다.

2. 부울 회로

다수결 게이트는 부울 회로에서 입력의 과반수가 참일 때 참을 출력하는 논리 게이트이다. 전가산기에서 자리올림수(캐리) 출력은 세 개의 입력에 다수결 함수를 적용하여 구할 수 있지만, 종종 가산기의 이 부분은 여러 개의 더 간단한 논리 게이트로 분해된다.

2. 1. 회로 복잡도

회로 복잡도 이론에서 다수결 함수는 AC0 회로에서 2^{o(n)}으로 계산할 수 없다는 것이 증명되었다.[1] 이는 다수결 함수가 특정 복잡도 클래스에 속하지 않음을 의미한다.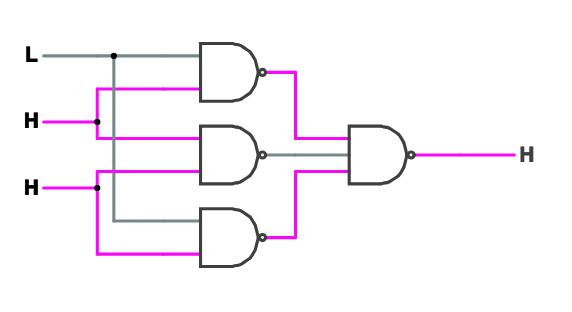

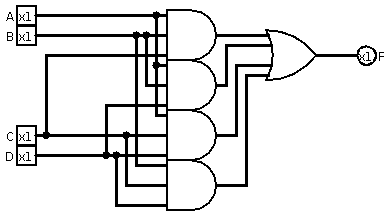
3비트 다수결 회로


4비트 다수결 회로

2. 2. 응용

다수결 게이트는 전가산기에서 자리올림수 출력을 계산하거나, 오류 정정을 위한 다수결 논리 디코딩에 사용된다. 많은 시스템에서 3중 모듈 중복성을 사용하며, 오류 수정을 위해 다수결 함수를 활용한다. 예를 들어, 전가산기에서 자리올림수 출력은 3개의 입력에 다수결 함수를 적용하여 구할 수 있다.

3. 성질

3진 다수결 함수 <x, y, z>는 다음 성질을 만족한다.[1]


  • <x, y, y> = y
  • <x, y, z> = <z, x, y>
  • <x, y, z> = <x, z, y>
  • <<x, w, y>, w, z> = <x, w, <y, w, z>>


이러한 대수 구조를 중앙값 대수라 한다. 임의의 ''x'', ''y'', ''z''에 대해 삼항 중앙값 연산자 ⟨''x'', ''y'', ''z''⟩는 다음 방정식을 만족한다.[1]

  • ⟨''x'', ''y'', ''y''⟩ = ''y''
  • ⟨''x'', ''y'', ''z''⟩ = ⟨''z'', ''x'', ''y''⟩
  • ⟨''x'', ''y'', ''z''⟩ = ⟨''x'', ''z'', ''y''⟩
  • ⟨⟨''x'', ''w'', ''y''⟩, ''w'', ''z''⟩ = ⟨''x'', ''w'', ⟨''y'', ''w'', ''z''⟩⟩


이러한 공리를 만족하는 추상적인 시스템은 중앙값 대수이다.[1]

4. 다수결 함수의 일반화

''n'' = 1일 때에는 항등 함수 ''x''가 되고, ''n'' = 3일 때에는 ''xy'' + ''yz'' + ''zx''가 된다. 이때 +는 논리합이나 배타적 논리합이나 같은 결과를 도출한다. 임의의 ''n''에 대해 크기가 O(''n''5.3)인 다수결 함수에 대한 단조 공식이 존재하지만 이는 확률적 방법에 의한 비구성적 증명이다.[3]

다항식 크기의 명시적 다수결 공식을 위한 접근 방식은 다음과 같다.


  • 각 비교-교환 "와이어"가 단순히 OR 게이트와 AND 게이트인 정렬 네트워크에서 중앙값을 취한다. 아지-콤로스-세메레디 (AKS) 구조가 그 예이다.
  • 더 작은 다수결 회로의 출력을 결합한다.[4]

5. 동률 (Ties)

대부분의 응용 프로그램은 입력값의 절반이 0이고 절반이 1인 경우(동률)를 방지하기 위해 의도적으로 홀수 개의 입력을 사용한다. 짝수 입력을 받는 시스템의 경우, 일부는 0으로 편향된 결과를 출력한다. 예를 들어, 4입력 다수결 게이트는 입력 중 2개 이상이 0일 때 0을 출력한다.[1] 일부 시스템에서는 무작위로 동률을 해소한다.[2]

참조

[1] 서적 Error-correcting Codes https://archive.org/[...] MIT Press
[2] 간행물 Majority Rules with Random Tie-Breaking in Boolean Gene Regulatory Networks Public Library of Science 2013-07
[3] 간행물 Short monotone formulae for the majority function
[4] 간행물 Depth Two Majority Circuits for Majority and List Expanders Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik 2018
[5] 서적 Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques Springer 2006


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com