받아올림
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
받아올림은 덧셈에서 각 자릿수의 합이 10을 넘어갈 때 윗자리로 1을 올리는 것이며, 뺄셈에서는 윗자리에서 10을 빌려오는 빌림이 발생한다. 이러한 개념은 수동 연산, 수학교육, 고등 수학, 기계식 계산기, 컴퓨터 연산 등 다양한 분야에서 나타난다. 특히 기계식 계산기에서는 받아올림 구현이 중요한 과제였으며, 컴퓨터에서는 캐리 비트를 통해 연산을 처리한다.
더 읽어볼만한 페이지
- 수학 교육 - 구구단
구구단은 곱셈을 간편하게 계산하도록 곱셈 결과를 표로 정리한 것이며, 1단부터 9단까지 외우는 곱셈 구구가 일반적이고, 덧셈, 뺄셈, 나눗셈 구구 등 다양한 형태가 존재하며, 수학적 개념 이해의 기초가 되고 실생활에도 응용된다. - 수학 교육 - 산술
산술은 수의 계산을 다루는 수학 분야로, 사칙연산을 기본으로 하여 수론, 유리수 산술, 실수 산술 등 다양한 분야를 포함하며 여러 학문 분야에 응용된다. - 산수 - 계산
계산은 수나 식을 이용해 연산을 하거나 주어진 정보로 결과를 내는 행위로, 어원은 각각 석회에서 유래한 'calculation'과 '함께 계산하다'라는 뜻의 'computation'이며, 계산기나 컴퓨터 등의 도구를 통해 수행된다. - 산수 - 최소공배수
최소공배수는 둘 이상의 정수들의 공배수 중 가장 작은 양의 정수로서, 소인수분해나 최대공약수와의 관계를 이용하여 구할 수 있으며, 분수 통분이나 기어 회전 수 계산 등 여러 분야에 응용된다. - 컴퓨터 산술 - IEEE 754
IEEE 754는 부동소수점 숫자를 표현하고 처리하기 위한 국제 표준으로, 다양한 형식과 연산, 반올림 규칙, 예외 처리 등을 정의한다. - 컴퓨터 산술 - 1의 보수
1의 보수는 이진수에서 양수는 일반적인 이진수로, 음수는 양수의 각 비트를 반전시켜 표현하며, 덧셈 시 자리올림수가 발생하면 결과값에 더해야 하고, 0을 중복 표현하는 단점으로 현대에는 2의 보수가 주로 사용된다.
| 받아올림 |
|---|
2. 수동 연산
수동 연산은 펜과 종이를 이용하여 계산하는 방법을 말한다. 덧셈에서는 받아올림이, 뺄셈에서는 빌림이 사용된다.[1]
2. 1. 덧셈에서의 받아올림
전형적인 받아올림의 예는 펜과 종이를 이용한 덧셈에서 볼 수 있다.[1]:27
:+59
:----
:86
7 + 9 = 16이고, 숫자 1이 받아올림이다.
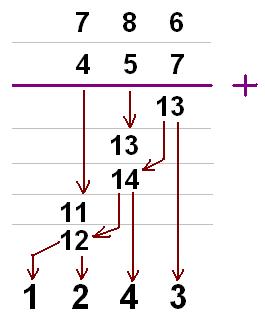
2. 2. 뺄셈에서의 빌림
전형적인 받아올림의 반대 경우는 뺄셈에서 볼 수 있는 '''빌림'''이다.47
- 19
- ---
28
여기서, 7 - 9 = -2 이므로 (10 - 9) + 7 = 8을 시도하고, 10은 왼쪽의 다음 자릿수에서 ("빌려") 얻는다. 이것은 일반적으로 두 가지 방법으로 가르친다.
1. 10은 왼쪽 다음 자릿수에서 ''옮겨지고'', 이 예에서는 십의 자리에 3 - 1이 남는다. 이 방법에 따르면, "빌림"이라는 용어는 10을 다시 돌려주지 않으므로 잘못된 명칭이다.
2. 10은 왼쪽 다음 자릿수에서 ''복사''되고, 그런 다음 '빌린' 자릿수의 빼는 수에 더하여 ('돌려')주어, 이 예에서는 십의 자리에 4 - (1 + 1)이 된다.
3. 수학교육
전통적으로 받아올림은 초등학교 2학년 또는 1학년 후반에 여러 자릿수의 덧셈을 가르칠 때 다루어졌다. 그러나 20세기 후반 이후 미국에서 널리 채택된 TERC와 같은 많은 교육과정에서는 전통적인 방법 대신 자기 창안 연산 방법과 색칠, 조작 자료, 차트를 사용하는 방법을 채택하였다. 이러한 생략은 Mathematically Correct와 같은 단체들의 비판을 받았으며, 일부 주와 교육구에서는 이러한 시도를 포기했지만, 여전히 널리 사용되고 있다.
3. 1. 전통적인 교육 방법
전통적으로 받아올림은 초등학교 2학년 또는 1학년 후반에 여러 자릿수의 덧셈을 가르칠 때 다루어졌다. 그러나 20세기 후반 이후 미국에서 널리 채택된 TERC와 같은 많은 교육과정에서는 전통적인 받아올림 방법 대신 자기 창안 연산 방법과 색칠, 조작 자료, 차트를 사용하는 방법을 채택하였다. 이러한 생략은 Mathematically Correct와 같은 단체들의 비판을 받았으며, 일부 주와 교육구에서는 이러한 시도를 포기했지만, 여전히 널리 사용되고 있다.3. 2. 대안적인 교육 방법
20세기 후반 이후 미국에서 널리 채택된 TERC와 같은 많은 교육과정에서는 전통적인 받아올림 방법 대신 자기 창안 연산 방법과 색칠, 조작 자료, 차트를 사용하는 방법을 채택하였다. 이러한 생략은 Mathematically Correct와 같은 단체들의 비판을 받았으며, 일부 주와 교육구에서는 이러한 시도를 포기했지만, 여전히 널리 사용되고 있다.4. 고등 수학
고등 수학에서 받아올림은 단순한 연산을 넘어 다양한 수학 분야와 연결되는 개념으로 확장된다. 쿠머의 정리는 p진법 덧셈에서 발생하는 자리올림 횟수를 이항계수와 연결 짓고, 여러 자릿수 덧셈에서 자리올림 통계가 오일러 수 및 리플 셔플 순열과 관련된다는 것을 보여준다. 추상대수학에서는 자리올림 연산을 군 코호몰로지를 통해 공식화하고, 이를 실수의 특징 분석에 응용하기도 한다.[1][2][3][4][5][6][7][8][9]
4. 1. 쿠머의 정리
쿠머의 정리는 p진법으로 두 수를 더할 때 발생하는 자리올림 횟수가 특정 이항계수를 나누는 p의 최고차항의 지수와 같다는 것을 명시한다.4. 2. 오일러 수 및 리플 셔플 순열과의 관련성
여러 자릿수의 덧셈에서 자리올림 자릿수의 통계는 오일러 수 및 리플 셔플 순열의 통계와 관련이 있다.[1][2][3][4]4. 3. 추상대수학에서의 공식화
추상대수학에서 두 자릿수에 대한 자리올림 연산은 군 코호몰로지의 언어를 사용하여 공식화할 수 있다.[5][6][7] 이 관점은 실수의 대안적 특징에 적용될 수 있다.[8][9]5. 기계식 계산기
기계식 계산기에서 받아올림은 덧셈 후 별도의 주기로 실행된다. 덧셈 중에는 자리올림이 바로 수행되지 않고 "신호"만 되며, 이후 주기에서 해당 자릿수 위의 숫자를 증가시킨다.
파스칼의 계산기는 0에서 9로 숫자가 증가할 때 에너지를 저장하고, 9에서 0으로 바뀔 때 이 에너지를 방출하여 윗자리를 1만큼 증가시키는 방식을 사용했다. 파스칼은 추와 중력을, 컴토미터는 스프링을 사용했다.
일부 기계는 연속 전달 방식을 사용하는데, 숫자를 1 더하면 다음 자릿수가 1/10만큼 전진한다. 체비쇼프 계산기[10], 셀링의 설계[11] 등이 이 방식을 시도했으나 성공하지 못했다. 마르샹 계산기는 1930년대에 연속 전달 방식을 성공적으로 구현했고, 마르샹은 1960년대 후반까지 이 방식을 사용했다.
5. 1. 받아올림 구현의 어려움
자리올림은 기계식 계산기 설계자와 제작자가 직면하는 기본적인 과제 중 하나이다. 그들은 두 가지 기본적인 어려움에 직면한다. 첫 번째는 자리올림이 여러 자릿수의 변경을 필요로 한다는 사실에서 비롯된다. 999에 1을 더하려면 기계는 4개의 다른 자릿수를 증가시켜야 한다. 또 다른 과제는 자리올림이 다음 자릿수의 덧셈 연산이 완료되기 전에 "발생"할 수 있다는 점이다.[10][11]5. 2. 받아올림 구현 방식
대부분의 기계식 계산기는 덧셈 자체 후 별도의 자리올림 주기를 실행하여 자리올림을 구현한다. 덧셈 중에는 각 자리올림이 수행되는 것이 아니라 "신호"되며, 자리올림 주기 동안 기계는 "트리거"된 자릿수 위의 자릿수를 증가시킨다. 자리올림을 더하는 것이 다음 자릿수에서 새로운 자리올림을 생성할 수 있으므로, 이 연산은 일의 자리, 십의 자리, 백의 자리 등으로 순차적으로 수행되어야 한다.[10]몇몇 기계, 특히 두 번째로 제작된 계산기이자 가장 오래된 기계인 파스칼의 계산기는 다른 방법을 사용한다. 0에서 9로 자릿수를 증가시키면 에너지를 저장하는 기계 장치가 작동되고, 9에서 0으로 자릿수를 이동시키는 다음 증가는 이 에너지를 방출하여 다음 자릿수를 1만큼 증가시킨다. 파스칼은 그의 기계에 추와 중력을 사용했다. 유사한 방법을 사용하는 또 다른 주목할 만한 기계는 매우 성공적인 19세기 컴토미터로, 추를 스프링으로 대체했다.
일부 혁신적인 기계는 연속 전달을 사용한다. 어떤 자릿수에 1을 더하면 다음 자릿수가 1/10만큼 전진하고(이는 다시 다음 자릿수를 1/100만큼 전진시키는 등), 이런 식으로 진행된다. 1870년의 체비쇼프 계산기와[10] 1886년의 셀링의 설계 등[11] 일부 혁신적인 초기 계산기는 이 방법을 사용했지만, 성공적이지 못했다. 1930년대 초, 마르샹 계산기는 "사일런트 스피드(Silent Speed)" 계산기로 시작하여 연속 전달을 큰 성공을 거두며 구현했다. 마르샹(후에 SCM Corporation)은 계속해서 이를 사용하고 개선하여 기계식 계산기 시대의 끝인 1960년대 후반까지 타의 추종을 불허하는 속도를 가진 연속 전달 계산기를 제작했다.
5. 3. 파스칼의 계산기 및 컴토미터
파스칼의 계산기는 0에서 9로 자릿수를 증가시키면서 에너지를 저장하는 기계 장치를 작동시키고, 9에서 0으로 자릿수를 이동시키는 다음 증가에서 이 에너지를 방출하여 다음 자릿수를 1만큼 증가시키는 방식을 사용하였다. 파스칼은 그의 기계에 추와 중력을 사용했다.[10] 이와 유사한 방법을 사용한 또 다른 주목할 만한 기계는 19세기의 컴토미터인데, 추를 스프링으로 대체했다.[11]5. 4. 연속 전달 방식
몇몇 혁신적인 기계는 연속 전달을 사용한다. 어떤 자릿수에 1을 더하면 다음 자릿수가 1/10만큼 전진하고(이는 다시 다음 자릿수를 1/100만큼 전진시키는 등), 이런 식으로 진행된다. 1870년의 체비쇼프 계산기[10]와 1886년의 셀링의 설계[11] 등 일부 혁신적인 초기 계산기는 이 방법을 사용했지만, 성공적이지 못했다. 1930년대 초, 마르샹 계산기는 "사일런트 스피드(Silent Speed)" 계산기로 시작하여 연속 전달을 큰 성공을 거두며 구현했다. 마르샹(후에 SCM Corporation)은 계속해서 이를 사용하고 개선하여 기계식 계산기 시대의 끝인 1960년대 후반까지 타의 추종을 불허하는 속도를 가진 연속 전달 계산기를 제작했다.6. 컴퓨터 연산
가산기와 같은 디지털 회로에서 "캐리"(carry)는 비슷한 의미로 사용된다.
6. 1. 캐리 비트
대부분의 컴퓨터에서 산술 연산의 최상위 비트로부터의 캐리(또는 시프트 연산에서 시프트되어 나온 비트)는 특수한 ''캐리 비트''에 저장된다. 이 비트는 다중 정밀도 산술 연산의 캐리 입력으로 사용되거나, 테스트되어 컴퓨터 프로그램의 실행을 제어하는 데 사용될 수 있다. 같은 ''캐리 비트''는 뺄셈에서의 자리 빌림을 나타내는 데에도 사용되지만, 2의 보수 산술의 영향으로 비트의 의미가 반전된다.일반적으로 캐리 비트 값이 "1"이라는 것은 덧셈이 ALU의 범위를 초과했음을 의미하며, CPU의 길이보다 긴 데이터 단어를 더할 때 고려해야 한다. 뺄셈 연산의 경우, 대부분의 기계는 자리 빌림 시 캐리 플래그를 설정하는 반면, 일부 기계(예: 6502, PIC)는 자리 빌림 시 캐리 플래그를 재설정하는 등 두 가지(반대되는) 규칙이 사용된다.
캐리는 정수 오버플로를 유발할 수 있다.
6. 2. 캐리 비트의 활용
대부분의 컴퓨터에서 산술 연산의 최상위 비트로부터의 캐리(또는 시프트 연산에서 시프트되어 나온 비트)는 특수한 ''캐리 비트''에 저장된다. 이 비트는 다중 정밀도 산술 연산의 캐리 입력으로 사용되거나, 테스트되어 컴퓨터 프로그램의 실행을 제어하는 데 사용될 수 있다. 같은 ''캐리 비트''는 일반적으로 뺄셈에서의 자리 빌림을 나타내는 데에도 사용되지만, 2의 보수 산술의 영향으로 비트의 의미가 반전된다. 일반적으로 캐리 비트 값이 "1"이라는 것은 덧셈이 ALU의 범위를 초과했음을 의미하며, CPU의 길이보다 긴 데이터 단어를 더할 때 고려해야 한다. 뺄셈 연산의 경우, 대부분의 기계는 자리 빌림 시 캐리 플래그를 설정하는 반면, 일부 기계(예: 6502, PIC)는 자리 빌림 시 캐리 플래그를 재설정하는 등 두 가지(반대되는) 규칙이 사용된다.캐리는 정수 오버플로를 유발할 수 있다.
6. 3. 뺄셈에서의 캐리 비트
대부분의 컴퓨터에서 산술 연산의 최상위 비트로부터의 캐리(또는 시프트 연산에서 시프트되어 나온 비트)는 특수한 ''캐리 비트''에 저장된다. 이 비트는 다중 정밀도 산술 연산의 캐리 입력으로 사용되거나, 컴퓨터 프로그램의 실행을 제어하는 데 사용될 수 있다. 같은 ''캐리 비트''는 뺄셈에서의 자리 빌림을 나타내는 데에도 사용되지만, 2의 보수 산술의 영향으로 비트의 의미가 반전된다. 일반적으로 캐리 비트 값이 "1"이라는 것은 덧셈이 ALU의 범위를 초과했음을 의미하며, CPU의 길이보다 긴 데이터 단어를 더할 때 고려해야 한다. 뺄셈 연산의 경우, 대부분의 기계는 자리 빌림 시 캐리 플래그를 설정하는 반면, 일부 기계(예: 6502, PIC)는 자리 빌림 시 캐리 플래그를 재설정하는 등 두 가지(반대되는) 규칙이 사용된다.6. 4. 정수 오버플로
대부분의 컴퓨터에서 산술 연산 최상위 비트로부터의 캐리(또는 시프트 연산에서 시프트되어 나온 비트)는 특수한 ''캐리 비트''에 저장된다. 이 비트는 다중 정밀도 산술 연산의 캐리 입력으로 사용되거나, 테스트되어 컴퓨터 프로그램의 실행을 제어하는 데 사용될 수 있다. 일반적으로 캐리 비트 값이 "1"이라는 것은 덧셈이 ALU의 범위를 초과했음을 의미하며, CPU의 길이보다 긴 데이터 단어를 더할 때 고려해야 한다. 캐리는 정수 오버플로를 유발할 수 있다.[1]참조
[1]
논문
Carries, Combinatorics, and an Amazing Matrix
1997-02-01
[2]
논문
Carries, shuffling, and symmetric functions
2009-08-01
[3]
논문
On adding a list of numbers (and other one-dependent determinantal processes)
2010-10-01
[4]
논문
A generalization of carries processes and Eulerian numbers
2014-02-01
[5]
논문
Linear Bijections and the Fast Fourier Transform
1997-01-01
[6]
논문
A Cohomological Viewpoint on Elementary School Arithmetic
http://www.math.wayn[...]
2014-01-22
[7]
서적
Mathematics under the Microscope: Notes on Cognitive Aspects of Mathematical Practice
American Mathematical Society
2010-01-01
[8]
논문
Significance Arithmetic: The Carrying Algorithm
1973-05-01
[9]
논문
The Real Numbers as a Wreath Product
1975-06-01
[10]
웹사이트
Chebyshev's continuous adding machine
https://locomat.lori[...]
2015-01-01
[11]
서적
The Calculating Machines
http://www.rechenmas[...]
Charles Babbage Institute
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com