등엔트로피 과정

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 배경
- 2.1. 열역학 제2법칙과 엔트로피
- 2.2. 가역 과정과 비가역 과정
3. 열역학 시스템에서의 등엔트로피 과정
4. 열역학 사이클에서의 등엔트로피 과정
- 4.1. 주요 열역학 사이클
5. 등엔트로피 유동
참조

1. 개요

등엔트로피 과정은 열역학 과정의 한 종류로, 시스템의 엔트로피가 일정하게 유지되는 과정을 의미한다. 이 과정은 가역적 단열 과정으로, 열의 출입이 없고 시스템 내부의 엔트로피 변화가 없다.

등엔트로피 과정은 열역학 제2법칙과 관련되어 있으며, 열역학 시스템, 열역학 사이클, 유체역학 등 다양한 분야에서 중요한 개념으로 활용된다. 이론적으로 펌프, 가스 압축기, 터빈, 노즐, 디퓨저 등의 열역학 장치가 등엔트로피 과정으로 작동하며, 카르노 사이클, 랭킨 사이클, 오토 사이클 등 다양한 열역학 사이클에서 압축 또는 팽창 단계에 포함된다. 유체역학에서는 단열적이고 가역적인 유체 유동을 등엔트로피 유동이라고 하며, 이상 기체의 등엔트로피 유동에 대한 관계식을 유도할 수 있다.

2. 배경

열역학 제2법칙은 자연 현상의 비가역성을 설명하며, 엔트로피 개념을 도입한다. 등엔트로피 과정은 이러한 열역학 제2법칙의 특수한 경우에 해당한다. 가역 등엔트로피 과정은 단열 과정이지만, 비가역 등엔트로피 과정은 단열 과정이 아니다.

가역 과정에서 등엔트로피 변화는 주변 환경으로부터 계를 열적으로 "절연"함으로써 이루어진다. 온도는 엔트로피의 열역학적 공액 변수이며, 따라서 공액 과정은 등온 과정이다. 등온 과정에서 계는 외부(항온조)와 열적으로 "접속"되어 있다.

2. 1. 열역학 제2법칙과 엔트로피

열역학 제2법칙에 따르면 다음이 성립한다.^[8]^[9]

:

T_\text{surr}dS \ge \delta Q,

여기서

\delta Q

는 시스템이 가열을 통해 얻는 에너지의 양이고,

T_\text{surr}

은 주변의 온도이며,

dS

는 엔트로피의 변화이다. 등호는 시스템과 주변의 온도가 본질적으로 동일하며 물리적 현실에서는 실제로 발생하지 않는 상상의 이상적인 이론적 한계인 가역 과정을 나타낸다.^[10]^[11] 등엔트로피 과정의 경우, 가역적이라면 과정이 단열 과정이므로 열로서의 에너지 전달이 없다. 즉, ''δQ'' = 0이다. 반대로, 과정이 비가역적이라면 시스템 내에서 엔트로피가 생성된다. 결과적으로 시스템 내에서 일정한 엔트로피를 유지하기 위해, 동시에 열로서 에너지를 시스템에서 제거해야 한다.

가역 과정의 경우, 등엔트로피 변환은 시스템을 주변 환경으로부터 열적으로 "단열"함으로써 수행된다. 온도는 엔트로피에 대한 열역학적 공액 변수이므로, 공액 과정은 시스템이 일정한 온도의 열원과 열적으로 "연결"되는 등온 과정이 될 것이다.

2. 2. 가역 과정과 비가역 과정

열역학 제2법칙은 다음과 같이 나타낸다.^[8]^[9]

:T^영어dS^영어 ≥ δQ^영어

여기서 δQ^영어는 시스템이 가열을 통해 얻는 에너지의 양이고, T^영어는 주변의 온도이며, dS^영어는 엔트로피의 변화이다. 등호는 시스템과 주변의 온도가 본질적으로 동일하며 물리적 현실에서는 실제로 발생하지 않는 상상의 이상적인 이론적 한계인 가역 과정을 나타낸다.^[10]^[11]

등엔트로피 과정의 경우, 가역적이라면 과정이 단열 과정이므로 열로서의 에너지 전달이 없다. 즉, ''δQ'' = 0이다. 반대로, 과정이 비가역적이라면 시스템 내에서 엔트로피가 생성된다. 결과적으로 시스템 내에서 일정한 엔트로피를 유지하기 위해, 동시에 열로서 에너지를 시스템에서 제거해야 한다.

가역 과정의 경우, 등엔트로피 변환은 시스템을 주변 환경으로부터 열적으로 "단열"함으로써 수행된다. 온도는 엔트로피에 대한 열역학적 공액 변수이므로, 공액 과정은 시스템이 일정한 온도의 열원과 열적으로 "연결"되는 등온 과정이 될 것이다.

3. 열역학 시스템에서의 등엔트로피 과정

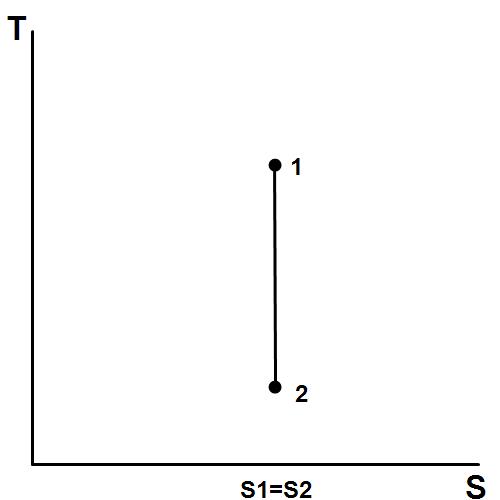
T–s (엔트로피 대 온도) 선도에서 등엔트로피 과정은 수직선으로 나타난다.

주어진 질량의 엔트로피는 내부적으로 가역적이고 단열적인 과정 동안 변하지 않는다. 이처럼 엔트로피가 일정하게 유지되는 과정을 등엔트로피 과정이라고 하며,

\Delta s=0

또는

s_1 = s_2

로 표기한다.^[12] 펌프, 가스 압축기, 터빈, 노즐, 디퓨저 등은 이론적으로 등엔트로피 과정으로 작동하는 열역학 장치의 예시이다.

등엔트로피 유동(isentropic flow)은 단열적이고 가역적인 유동이다. 즉, 유동에 에너지가 더해지지 않고, 마찰이나 소산에 의한 에너지 손실도 일어나지 않는다. 이상 기체의 등엔트로피 유동에서 유선에 따른 압력, 밀도, 온도의 관계식을 정의할 수 있다.

3. 1. 등엔트로피 과정의 정의

주어진 질량의 엔트로피는 내부적으로 가역적이고 단열 과정 동안 변하지 않는다. 엔트로피가 일정하게 유지되는 과정을 등엔트로피 과정이라고 하며,

\Delta s=0

또는

s_1 = s_2

로 표기한다.^[12] 이론적으로 등엔트로피 열역학 장치의 몇 가지 예로는 펌프, 가스 압축기, 터빈, 노즐, 디퓨저 등이 있다.

열역학 제2법칙에 따르면 다음이 성립한다.

:

\delta Q \le TdS

여기서,

\delta Q

는 가열에 의해 계가 획득하는 에너지량,

T

는 계의 온도,

dS

는 엔트로피의 변화량이다. 등호가 있는 것은 가역 과정의 경우를 의미한다. 가역 등엔트로피 과정에서는 외부와의 열에너지 교환이 없으므로 단열 과정이기도 하다. 비가역 과정의 경우 엔트로피는 증가한다. 따라서 계로부터 열을 빼앗아(냉각하여) 내부 엔트로피를 일정하게 유지하여 등엔트로피 비가역 과정으로 한다. 따라서 비가역 등엔트로피 과정은 단열 과정이 아니다.

가역 과정의 경우 등엔트로피 변화는 주변 환경으로부터 그 계를 열적으로 "절연"함으로써 이루어진다. 온도는 엔트로피의 열역학적 공액 변수이며, 따라서 공액 과정은 등온 과정이다. 등온 과정에서는 계는 외부(항온조)와 열적으로 "접속"되어 있다.

3. 2. 등엔트로피 장치의 예

펌프, 가스 압축기, 터빈, 노즐, 디퓨저 등은 이론적으로 등엔트로피 과정으로 작동하는 장치이다.^[12]

3. 3. 정상 유동 장치의 등엔트로피 효율

대부분의 정상 유동 장치는 단열 조건에서 작동하며, 이러한 장치의 이상적인 과정은 등엔트로피 과정이다. 장치가 해당 등엔트로피 장치에 얼마나 효율적으로 근사하는지를 설명하는 매개변수를 등엔트로피 효율 또는 단열 효율이라고 한다.^[12]

터빈의 등엔트로피 효율:

:

\eta_\text{t} = \frac{\text{실제 터빈 일}}{\text{등엔트로피 터빈 일}} = \frac{W_a}{W_s} \cong \frac{h_1 - h_{2a}}{h_1 - h_{2s}}.

압축기의 등엔트로피 효율:

:

\eta_\text{c} = \frac{\text{등엔트로피 압축기 일}}{\text{실제 압축기 일}} = \frac{W_s}{W_a} \cong \frac{h_{2s} - h_1}{h_{2a} - h_1}.

노즐의 등엔트로피 효율:

:

\eta_\text{n} = \frac{\text{노즐 출구에서 실제 KE}}{\text{노즐 출구에서 등엔트로피 KE}} = \frac{V_{2a}^2}{V_{2s}^2} \cong \frac{h_1 - h_{2a}}{h_1 - h_{2s}}.

위의 모든 방정식에서:

''h''₁은 입구 상태에서의 엔탈피 이고,
''h''_2a는 실제 과정의 출구 상태에서의 비 엔탈피이며,
''h''_2s는 등엔트로피 과정의 출구 상태에서의 비 엔탈피이다.

4. 열역학 사이클에서의 등엔트로피 과정

여러 열역학 사이클에서 등엔트로피 과정은 중요한 부분을 차지한다. 하지만 등엔트로피 가정은 이상적인 사이클에만 적용된다. 실제 사이클은 압축기 및 터빈의 비효율성과 열역학 제2법칙으로 인해 내재적인 손실을 겪는다. 실제 시스템은 진정한 등엔트로피 상태가 아니지만, 등엔트로피 거동은 많은 계산 목적에 적절한 근사치이다.^[1]

4. 1. 주요 열역학 사이클

주요 열역학 사이클에서의 등엔트로피 과정
사이클	등엔트로피 단계	설명
랭킨 사이클	1→2	펌프 내 등엔트로피 압축
랭킨 사이클	3→4	터빈 내 등엔트로피 팽창
카르노 사이클	2→3	등엔트로피 팽창
카르노 사이클	4→1	등엔트로피 압축
오토 사이클	1→2	등엔트로피 압축
오토 사이클	3→4	등엔트로피 팽창
디젤 사이클	1→2	등엔트로피 압축
디젤 사이클	3→4	등엔트로피 팽창
브레이튼 사이클	1→2	압축기 내 등엔트로피 압축
브레이튼 사이클	3→4	터빈 내 등엔트로피 팽창
증기 압축 냉동 사이클	1→2	압축기 내 등엔트로피 압축
르누아르 사이클	2→3	등엔트로피 팽창
자일리거 사이클	1→2	등엔트로피 압축
자일리거 사이클	4→5	등엔트로피 압축

참고: 등엔트로피 가정은 이상적인 사이클에만 적용된다. 실제 사이클은 압축기 및 터빈의 비효율성과 열역학 제2법칙으로 인해 내재적인 손실을 겪는다. 실제 시스템은 진정한 등엔트로피는 아니지만, 등엔트로피 거동은 많은 계산 목적에 적절한 근사치이다.

5. 등엔트로피 유동

유체역학에서 '''등엔트로피 유동'''은 단열 과정이면서 가역 과정인 유체 유동이다. 즉, 유동에 열이 더해지지 않으며, 마찰이나 소산 효과로 인한 에너지 변환이 일어나지 않는다. 이상 기체의 등엔트로피 유동의 경우, 유선을 따라 압력, 밀도 및 온도를 정의하기 위해 여러 관계를 도출할 수 있다.^[1]

등엔트로피 변환에서는 열 교환이 일어나지 않는 한 에너지를 유동과 교환할 수 있다. 그러한 교환의 예로는 유동에 의해 또는 유동에 대한 일을 수반하는 등엔트로피 팽창 또는 압축이 있다.^[1]

엔트로피 밀도가 모든 곳에서 동일하면, 유동은 균등 엔트로피라고 한다.^[1]

5. 1. 등엔트로피 유동의 정의

유체역학에서 '''등엔트로피 유동'''은 단열 과정이면서 가역적인 유체 유동이다. 즉, 유동에 열이 더해지지 않으며, 마찰 또는 소산 효과로 인한 에너지 변환이 일어나지 않는다. 이상 기체의 등엔트로피 유동의 경우, 유선(streamline)을 따라 압력, 밀도 및 온도를 정의하기 위해 여러 관계를 도출할 수 있다.

5. 2. 이상 기체의 등엔트로피 유동

유체역학에서, 이상 기체의 등엔트로피 유동은 유선(streamline)을 따라 압력, 밀도 및 온도를 정의하는 여러 관계식을 도출할 수 있다.

등엔트로피 유동은 단열 과정이면서 가역 과정인 유체 유동이다. 즉, 유동에 열이 더해지지 않으며, 마찰 또는 소산 효과로 인한 에너지 변환이 일어나지 않는다.

등엔트로피 변환에서는 열 교환이 일어나지 않는 한, 에너지를 유동과 교환할 수 있다. 그러한 교환의 예로는 유동에 의해 또는 유동에 대한 일을 수반하는 등엔트로피 팽창 또는 압축이 있다.

폐쇄계에서 계 전체의 에너지 변화는 행해진 일과 추가된 열의 총합이다.

:

dU = dW + dQ\,\!

부피 변화로 계가 한 일은 다음 식으로 나타낸다.

:

dW = -pdV\,\!

여기서

p

는 압력,

V

는 부피이다. 엔탈피 (

H = U + pV\,\!

)의 변화는 다음과 같다.

:

dH = dU + pdV + Vdp = n C_p dT\,\!

가역 과정은 단열 과정이므로 (즉, 열을 외부와 주고받지 않음),

dQ = 0, dS=0\,\!

이다. 여기서 다음의 중요한 두 식이 유도된다.

:

dU = -pdV\,\!

, 그리고

:

dH = Vdp\,\!

또는

dQ = dH - Vdp = 0\,\!

:

dQ = TdS\,\!

⇒

dS = (1/T) dH - (V/T) dp\,\!

그러면 비열비는 다음과 같다.

:

\gamma = \frac{C_p}{C_V} = -\frac{dp/p}{dV/V}\,\!

이상 기체에서는

\gamma\,\!

는 상수이므로, 이상 기체임을 전제로 위의 식을 적분하면 다음을 얻는다.

:

pV^{\gamma} = \mbox{constant} \,

이므로

:

\frac{p_2}{p_1} = \left(\frac{V_1}{V_2}\right)^{\gamma}

이상 기체의 상태 방정식

p V = n R T\,\!

를 사용하면 다음과 같다.

:

TV^{\gamma-1} = \mbox{constant} \,

:

\frac{p^{\gamma -1}}{T^{\gamma}} = \mbox{constant}

또한,

C_p = C_v + R

(몰 단위)가 성립하므로,

:

\frac{V}{T} = \frac{nR}{p}

및

p = \frac{nRT}{V}

:

S_2-S_1 = nC_p \ln\left(\frac{T_2}{T_1}\right) - nR\ln\left(\frac{p_2}{p_1}\right)

:

\frac{S_2-S_1}{n} = C_p \ln\left(\frac{T_2}{T_1}\right) - R\ln\left (\frac{T_2V_1}{T_1V_2} \right ) = C_v\ln\left(\frac{T_2}{T_1}\right)+R \ln\left(\frac{V_2}{V_1}\right)

이상에서, 이상 기체의 등엔트로피 과정에 대해 다음이 성립한다.

:

T_2 = T_1\left(\frac{V_1}{V_2}\right)^{(R/C_v)}

또는

V_2 = V_1\left(\frac{T_1}{T_2}\right)^{(C_v/R)}

5. 3. 등엔트로피 관계식 유도

닫힌 계에서, 계의 총 에너지 변화는 수행된 일과 가해진 열의 합과 같다.

:

dU = \delta W + \delta Q.

부피 변화에 의해 계에 가해진 가역적인 일은

:

\delta W = -p \,dV,

여기서

p

는 압력이고,

V

는 부피이다. 엔탈피(

H = U + pV

)의 변화는 다음과 같다.

:

dH = dU + p \,dV + V \,dp.

가역적이고 단열적인 과정(즉, 열 전달이 없는 경우)에 대해

\delta Q_\text{rev} = 0

이므로,

dS = \delta Q_\text{rev}/T = 0

이다. 모든 가역 단열 과정은 등엔트로피적이다. 이로 인해 두 가지 중요한 관찰을 할 수 있다.

:

dU = \delta W + \delta Q = -p \,dV + 0,

:

dH = \delta W + \delta Q + p \,dV + V \,dp = -p \,dV + 0 + p \,dV + V \,dp = V \,dp.

이상 기체의 모든 변환에 대해 다음이 항상 참이다.

:

dU = n C_v \,dT

, and

dH = n C_p \,dT.

dU

와

dH

에 대해 위에 파생된 일반적인 결과를 사용하면,

:

dU = n C_v \,dT = -p \,dV,

:

dH = n C_p \,dT = V \,dp.

따라서 이상 기체의 경우, 비열비는 다음과 같이 쓸 수 있다.

:

\gamma = \frac{C_p}{C_V} = -\frac{dp/p}{dV/V}.

열적으로 완전한 기체의 경우,

\gamma

는 상수이다. 따라서 위 식을 적분하면, 열적으로 완전한 기체라고 가정할 때,

:

pV^\gamma = \text{constant},

즉,

:

\frac{p_2}{p_1} = \left(\frac{V_1}{V_2}\right)^\gamma.

이상 기체에 대한 상태 방정식

p V = n R T

를 사용하면,

:

TV^{\gamma-1} = \text{constant}.

(증명:

PV^\gamma = \text{constant} \Rightarrow PV\,V^{\gamma-1} = \text{constant} \Rightarrow nRT\,V^{\gamma-1} = \text{constant}.

그러나 ''nR'' 자체가 상수이므로

TV^{\gamma-1} = \text{constant}

이다.)

:

\frac{p^{\gamma-1}}{T^\gamma} = \text{constant}

또한, 상수

C_p = C_v + R

(1몰당)에 대해,

:

\frac{V}{T} = \frac{nR}{p}

and

p = \frac{nRT}{V}

:

S_2-S_1 = nC_p \ln\left(\frac{T_2}{T_1}\right) - nR\ln\left(\frac{p_2}{p_1}\right)

:

\frac{S_2-S_1}{n} = C_p \ln\left(\frac{T_2}{T_1}\right) - R\ln\left(\frac{T_2 V_1}{T_1 V_2}\right ) = C_v\ln\left(\frac{T_2}{T_1}\right)+ R \ln\left(\frac{V_2}{V_1}\right)

따라서 이상 기체의 등엔트로피 과정의 경우,

:

T_2 = T_1\left(\frac{V_1}{V_2}\right)^{(R/C_v)}

or

V_2 = V_1\left(\frac{T_1}{T_2}\right)^{(C_v/R)}

5. 4. 이상 기체의 등엔트로피 관계식

이상 기체의 등엔트로피 과정에서는 압력(

P

), 부피(

V

), 온도(

T

), 밀도(

\rho

) 사이에 다음과 같은 관계식이 성립한다.

관계식
$\frac {p_2} {p_1} = \left (\frac{T_2}{T_1} \right )^\frac {\gamma}{\gamma-1} = \left (\frac{\rho_2}{\rho_1} \right )^{\gamma} = \left (\frac{V_1}{V_2} \right )^{\gamma}$
$\frac {T_2} {T_1} = \left (\frac{p_2}{p_1} \right )^\frac {\gamma-1}{\gamma} = \left (\frac{\rho_2}{\rho_1} \right )^{(\gamma - 1)} = \left (\frac{V_1}{V_2} \right )^{(\gamma-1)}$
$\frac {\rho_2} {\rho_1} = \left (\frac{T_2}{T_1} \right )^\frac {1}{\gamma-1} = \left (\frac{p_2}{p_1} \right )^\frac {1}{\gamma} = \frac{V_1}{V_2}$
$\frac {V_2} {V_1} = \left (\frac{T_1}{T_2} \right )^\frac {1}{\gamma-1} = \frac{\rho_1}{\rho_2} = \left (\frac{p_1}{p_2} \right )^\frac {1}{\gamma}$

위 관계식은 다음 전제 조건에서 유도된다.

$pV^{\gamma} = \text{constant}$
$pV = m R_s T$
$p = \rho R_s T$

여기서,

$P$ = 압력
$V$ = 부피
$\gamma$ = 비열비 = $C_p/C_v$
$T$ = 온도
$m$ = 질량
$R_s$ = 특정 기체의 기체 상수 = $R/M$
$R$ = 표준 기체 상수
$M$ = 특정 기체의 분자량
$\rho$ = 밀도
$C_p$ = 정압 비열
$C_v$ = 정적 비열

참조

_[1] 서적 An Advanced Treatise on Physical Chemistry. Longmans, Green and Co.
_[2] 서적 A Course in Thermodynamics Blaisdell Publishing Company
_[3] 서적 Classical Thermodynamics Wiley–Interscience
_[4] 서적 Survey of Fundamental Laws, chapter 1 of Thermodynamics Academic Press
_[5] 서적 Fundamentals of Thermodynamics Wiley
_[6] 서적 Mechanics of Fluids Van Nostrand Reinhold Company
_[7] 서적 Thermodynamics: An Engineering Approach McGraw-Hill
_[8] 서적 Physical Chemistry Academic Press
_[9] 서적 Thermodynamics Dover Publications
_[10] 서적 Thermodynamics. An Advanced Treatment for Chemists and Physicists North Holland
_[11] 서적 A Course in Thermodynamics Blaisdell Publishing Company
_[12] 서적 Thermodynamics: An Engineering Approach Mcgraw-Hill
_[13] 서적 Fundamentals of Classical Thermodynamics
_[14] 서적 Mechanics of Fluids Van Nostrand Reinhold Company
_[15] 서적 An Advanced Treatise on Physical Chemistry. Longmans, Green and Co.
_[16] 서적 Survey of Fundamental Laws, chapter 1 of Thermodynamics Academic Press
_[17] 서적 Fundamentals of Thermodynamics Wiley
_[18] 서적 Mechanics of Fluids Van Nostrand Reinhold Company

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com