랭킨-위고니오 방정식

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 랭킨-위고니오 방정식 (Rankine-Hugoniot Equations)
참조

1. 개요

랭킨-위고니오 방정식은 충격파를 통과하는 유체의 상태 변화를 설명하는 데 사용되는 일련의 방정식이다. 이 방정식은 질량, 운동량, 에너지 보존 법칙에 기초하여 유도되며, 충격파의 앞뒤에서 유체의 밀도, 속도, 압력, 엔탈피 간의 관계를 나타낸다. 랭킨-위고니오 방정식은 수직 충격파, 정상 상태, 균일한 유체 상태, 이상 기체 및 단열 과정을 가정하여 유도된다. 이 방정식은 미셸슨-레일리 선과 후고니오 방정식을 포함하며, 고체에서의 충격파, 자기유체역학 등 다양한 분야에 적용된다.

더 읽어볼만한 페이지

유체역학 방정식 - 나비에-스토크스 방정식
나비에-스토크스 방정식은 유체의 운동을 기술하는 비선형 편미분방정식으로, 질량 및 운동량 보존 법칙에 기반하며, 해의 존재성과 매끄러움은 밀레니엄 문제이지만 다양한 유체 흐름 모델링과 수치 해석적 응용에 활용된다.
유체역학 방정식 - 베르누이 방정식
베르누이 방정식은 유체역학에서 유체의 속도, 압력, 높이 사이의 관계를 나타내며, 비압축성, 비점성, 정상류 조건에서 유선상 에너지 보존을 설명하고 항공기 양력 발생 등 다양한 분야에 응용되지만 실제 유체의 점성 등의 영향으로 적용에 한계가 있다.
스코틀랜드의 발명품 - 텔레비전
텔레비전은 움직이는 영상과 소리를 전기 신호로 변환하여 전송하고 수신 측에서 다시 영상과 소리로 바꾸는 기술을 이용한 매체로, 닙코프 원판을 이용한 초기 기계식 방식에서 음극선관 발명을 통해 전자식으로 발전하여 디지털 기술과 다양한 디스플레이 기술 발전을 거쳐 현재에 이르렀으며 사회, 문화, 경제적으로 큰 영향을 미치지만 건강 문제 및 부정적 콘텐츠 노출 등의 부작용도 존재한다.
스코틀랜드의 발명품 - 켈빈
켈빈은 국제단위계의 열역학 온도 기본 단위로, 볼츠만 상수를 통해 정의되며 절대 영도를 0 K로 하고 섭씨 온도는 켈빈 값에서 273.15를 뺀 값으로 계산되며 과학과 기술 분야에서 널리 활용된다.
연속체역학 - 온도
온도는 물체의 뜨겁고 차가운 정도를 나타내는 물리량으로, 열역학적으로는 에너지 이동 방향으로 정의되며, 미시적으로는 분자 운동 에너지의 평균값으로 정의되고, 화학 반응 속도와 생명체에 큰 영향을 미친다.
연속체역학 - 밀도
밀도는 단위 부피당 질량을 나타내는 물리량으로 질량을 부피로 나눈 값으로 계산되며, 온도와 압력에 따라 변하고, 진밀도, 겉보기밀도, 부피밀도, 탭밀도 등 여러 종류가 있고, 고대 그리스 시대부터 발전해왔다.

랭킨-위고니오 방정식
개요
종류	보존 법칙과 열역학 법칙을 따르는 방정식
관련 학문	유체 역학 열역학 기체 동역학
설명
정의	충격파 전후의 상태를 연관시키는 방정식
관련 과학자	윌리엄 존 매퀀 랭킨 피에르 앙리 위고니오
응용 분야	폭발 연소 고속 유체 역학
형태
질량 보존	ho_1 u_1 = ho_2 u_2
운동량 보존	p_1 + ho_1 u_1^2 = p_2 + ho_2 u_2^2
에너지 보존	h_1 + rac{1}{2} u_1^2 = h_2 + rac{1}{2} u_2^2
변수 설명	ho: 밀도 u: 유속 p: 압력 h: 비엔탈피
주의사항	위 식은 특정 좌표계에서 성립하며, 다양한 형태로 표현될 수 있음.

2. 랭킨-위고니오 방정식 (Rankine-Hugoniot Equations)

랭킨-위고니오 방정식은 충격파를 가로지르는 유체의 상태 변화를 나타내는 방정식으로, 질량, 운동량, 에너지 보존 법칙을 기반으로 유도된다.^[4]

불연속면과 함께 움직이는 좌표계에서 랭킨-위고니오 방정식은 다음과 같이 표현될 수 있다.^[4]

식	설명
$\rho_1\,u_1 = \rho_2\,u_2 \equiv m$	질량 보존
$\rho_1\,u_1^2 + p_1 = \rho_2\,u_2^2 + p_2$	운동량 보존
$h_1 + \frac{1}{2}u_1^2 = h_2 + \frac{1}{2}u_2^2$	에너지 보존

여기서 ''m''은 단위 면적당 질량 유량, ''ρ''₁과 ''ρ''₂는 파동의 상류와 하류 유체의 질량 밀도, ''u''₁과 ''u''₂는 파동의 상류와 하류 유체 속도, ''p''₁과 ''p''₂는 두 영역의 압력, ''h''₁과 ''h''₂는 두 영역의 (단위 질량당) 엔탈피이다.

질량 보존과 운동량 보존을 결합하면 다음과 같다.

: $\frac{p_2-p_1}{1/\rho_2-1/\rho_1}=-m^2$

이는 $p-\rho^{-1}$ 평면에서 음의 기울기를 갖는 '''미셸슨-레일리 선'''으로 표현된다. 이 직선은 러시아 물리학자 블라디미르 A. 미셸슨(일반적으로 미셸슨으로 영어화됨)과 레일리 경(Lord Rayleigh)의 이름을 따서 명명되었다.^[5]

질량 및 운동량 보존 방정식을 사용하여 ''u''₁ 및 ''u''₂를 제거하면, 에너지 보존 방정식은 다음과 같이 후고니오 방정식으로 표현될 수 있다.

: $h_2 - h_1 = \frac{1}{2}\,\left(\frac{1}{\rho_2}+\frac{1}{\rho_1}\right)\,(p_2 - p_1).$

여기서 밀도의 역수는 비체적 $v=1/\rho$ 으로 표현될 수 있다.

추가적으로, 상류 및 하류 상태 방정식 사이의 관계는 다음과 같이 주어진다.

: $f(p_1,\rho_1,T_1,Y_{i,1})=f(p_2,\rho_2,T_2,Y_{i,2})$

여기서 $Y_i$ 는 종의 질량 분율이다.

마지막으로, 열량 상태 방정식 $h=h(p,\rho,Y_i)$ 는 알려져 있다고 가정한다.

유동이 반응성인 경우, 종 보존 방정식은 다음과 같다.

: $\omega_{i,1}=\omega_{i,2}=0,\quad i = 1,2,3,\dots,N, \qquad \text{종 보존}$

이는 불연속면의 상류와 하류 모두에서 반응에 관련된 총 ''N''개의 종 중 ''i''번째 종의 질량 생성률 $\omega$ 이 0이 됨을 의미한다.

하나의 충격파에 의한 압축 한계를 조사하기 위해 이상 기체의 상태 방정식 $P = (\gamma-1)\rho\varepsilon$ 를 가정하면, 다음과 같은 관계를 얻을 수 있다.

: $\begin{align}&\frac{P_1V_1}{\gamma-1} - \frac{P_0V_0}{\gamma-1} = \frac{1}{2}(P_1+P_0)(V_0-V_1)\\\Rightarrow& \frac{V_1}{V_0} = \frac{(\gamma+1)P_0+(\gamma-1)P_1}{(\gamma-1)P_0 + (\gamma+1)P_1} \xrightarrow{P_1/P_0\rightarrow\infty} \frac{\gamma-1}{\gamma+1} .\end{align}$

즉, 복사 우세기 $\gamma=4/3$ 을 고려하면 원래 체적의 1/7까지 압축된다.

2. 1. 물리적 가정

랭킨-위고니오 방정식을 유도하기 위한 기본적인 가정은 다음과 같다.^[4]

수직 충격파: 평면 충격파가 그 면에 수직인 방향으로 전파되며, 흐름은 1차원적이다.
정상 상태: 파면에 고정된 좌표계를 사용하며, 흐름은 시간 변화하지 않는 것으로 한다.
충격파의 전후는 모두 균일한 상태이다.
유체는 이상 기체이며, 상태 변화는 단열 과정으로 한다.

2. 2. 방정식 유도 (무자기장, 이상 기체)

불연속면과 함께 움직이는 좌표계에서 랭킨-위고니오 방정식은 다음과 같이 표현된다.^[4]

식	설명
$\rho_1\,u_1 = \rho_2\,u_2 \equiv m$	질량 보존
$\rho_1\,u_1^2 + p_1 = \rho_2\,u_2^2 + p_2$	운동량 보존
$h_1 + \frac{1}{2}u_1^2 = h_2 + \frac{1}{2}u_2^2$	에너지 보존

여기서 ''m''은 단위 면적당 질량 유량, ''ρ''₁과 ''ρ''₂는 파동의 상류와 하류 유체의 질량 밀도, ''u''₁과 ''u''₂는 파동의 상류와 하류 유체 속도, ''p''₁과 ''p''₂는 두 영역의 압력, ''h''₁과 ''h''₂는 두 영역의 (단위 질량당) 엔탈피이다.

질량 보존과 운동량 보존을 결합하면 다음을 얻을 수 있다.

: $\frac{p_2-p_1}{1/\rho_2-1/\rho_1}=-m^2$

이는 $p-\rho^{-1}$ 평면에서 음의 기울기를 갖는 ( $m^2$ 은 항상 양수이므로) '''미셸슨-레일리 선'''이라고 알려진 직선을 정의하며, 러시아 물리학자 블라디미르 A. 미셸슨(일반적으로 미셸슨으로 영어화됨)과 레일리 경(Lord Rayleigh)의 이름을 따서 명명되었다.^[5]

질량 및 운동량 보존을 위한 랭킨-위고니오 방정식을 사용하여 ''u''₁ 및 ''u''₂를 제거하면, 에너지 보존 방정식은 후고니오 방정식으로 표현될 수 있다.

: $h_2 - h_1 = \frac{1}{2}\,\left(\frac{1}{\rho_2}+\frac{1}{\rho_1}\right)\,(p_2 - p_1).$

밀도의 역수는 비체적 $v=1/\rho$ 으로 표현될 수 있다.

이와 함께 상류 및 하류 상태 방정식 사이의 관계를 지정해야 한다.

: $f(p_1,\rho_1,T_1,Y_{i,1})=f(p_2,\rho_2,T_2,Y_{i,2})$

여기서 $Y_i$ 는 종의 질량 분율이다.

마지막으로, 열량 상태 방정식 $h=h(p,\rho,Y_i)$ 는 알려져 있다고 가정한다.

위의 물리적 가정을 바탕으로, 유체의 상태는 다음의 연속 방정식, 운동량 보존 및 에너지 보존에 의해 기술된다.

: $\begin{align}\frac{\partial\rho}{\partial t} &= -\frac{\partial(\rho u)}{\partial x} \\\frac{\partial(\rho u)}{\partial t} &= -\frac{\partial}{\partial x}(\rho u^2+p) \\\frac{\partial(\rho E)}{\partial t} &= -\frac{\partial}{\partial x}\left[\rho u\left(e+\frac{1}{2}u^2+\frac{p}{\rho}\right)\right]\end{align}$

여기서

''e'' : 비내부 에너지 혹은 비엔탈피 ([J/kg])
$E = e+\frac{1}{2}u^2$ : 총 에너지 ([J/kg])

이다. 또한 정상이므로 시간 미분항은 0이 되는 등의 가정을 사용하여 이것들을 적분하면, 다음의 식을 얻을 수 있다.

:

\begin{align}& Q \equiv \rho u = \rm{constant} \\& \rho u^2 + p = \rm{constant} \\& pu + Q\left(\frac{u^2}{2}+e\right) = \mathrm{constant}\end{align}

간단하게 하기 위해, 충격파는 평면으로,

x

방향으로만 전파되는 것으로 한다. 충격파가 통과하기 전의 영역(충격파 상류)과 충격파가 통과한 후의 영역(충격파 하류)에서 물리량은 불연속이 되며, 상류 측의 밀도, 속도, 단위 질량당 내부 에너지, 압력을

\rho_0, v_0,\varepsilon_0, P_0

로 하고, 하류 측의 밀도, 속도, 단위 질량당 내부 에너지, 압력을

\rho_1, v_1,\varepsilon_1,P_1

으로 한다.

질량(연속 방정식), 운동량, 에너지의 보존으로부터

:

\begin{align}\rho_0v_0 &= \rho_1v_1\\\rho_0v_0^2+P_0 &= \rho_1v_1^2 + P_1\\\left(\rho_0\varepsilon_0+\frac{1}{2}\rho_0v_0\right)v_0 + P_0v_0 &= \left(\rho_1\varepsilon_1+\frac{1}{2}\rho_1v_1\right)v_1+P_1v_1.\end{align}

제1식에서 제3식을 나누면

:

\begin{align}&\varepsilon_0 + \frac{1}{2} v_0^2 + \frac{P_0 }{\rho_0}= \varepsilon_1 + \frac{1}{2}v_1^2 + \frac{P_1}{\rho_1}\\\Rightarrow &h_1 -h_0 = \frac{1}{2}(v_0^2-v_1^2) \quad\mathrm{where}\quad h_i \equiv \varepsilon_i + \frac{P_i}{\rho_i}\end{align}

여기서,

h_i

는 단위 질량당 엔탈피이다. 또한 제1식을

:

\begin{align}\frac{\rho_1}{\rho_0} = \frac{v_0}{v_1} = \frac{V_0}{V_1}\quad\mathrm{where}\quad V_i \equiv \frac{1}{\rho_i}\end{align}

로 변형한다. 여기서

V_i

는 단위 질량당 체적이다. 그러면 제2식으로부터

:

\begin{align}&\rho_0 v_0^2 + P_ 0 = \frac{\rho_0^2}{\rho_1}v_0^2 + P_1\\\Rightarrow &v_0^2 = \frac{P_1-P_0}{\rho_0 - \frac{\rho_0^2}{\rho_1}} = \frac{P_1 - P_0}{\rho_0 - \frac{\rho_0^2}{\rho_1}} = V_0^2\frac{P_1-P_0}{V_0 -V_1}\\\Rightarrow& v_1^2 = V_1^2\frac{P_1-P_0}{V_0-V_1}.\end{align}

에서

:

\begin{align}v_0 - v_1 &= \left(1- \frac{V_1}{V_0}\right)v_0 = \left(1- \frac{V_1}{V_0}\right)V_0\sqrt{\frac{P_1-P_0}{V_0-V_1}}= \sqrt{(P_1 -P_0)(V_0-V_1)}\\v_0^2-v_1^2 &= (P_1-P_0)(V_0+V_1)\\\end{align}

엔탈피의 표식에 대입함으로써

:

h_1 -h_0 = \frac{1}{2}(P_1-P_0)(V_0+V_1)

를 얻는다. 혹은

:

\begin{align}\varepsilon_1 -\varepsilon_0 &= \frac{1}{2}(v_0^2-v_1^2)+V_0P_0 -V_1P_1 \\&=\frac{1}{2}(P_1-P_0)(V_0+V_1)+V_0P_0 -V_1P_1\\&=\frac{1}{2}(P_1+P_0)(V_0-V_1).\end{align}

이것을 '''랭킨-위고니오 관계(Rankin-Hugoniot relation)'''라고 부른다.

하나의 충격파에 의한 압축의 한계를 조사한다. 이상 기체의 경우, 상태 방정식

P = (\gamma-1)\rho\varepsilon

를 가정하면

:

\begin{align}&\frac{P_1V_1}{\gamma-1} - \frac{P_0V_0}{\gamma-1} = \frac{1}{2}(P_1+P_0)(V_0-V_1)\\\Rightarrow& \frac{V_1}{V_0} = \frac{(\gamma+1)P_0+(\gamma-1)P_1}{(\gamma-1)P_0 + (\gamma+1)P_1} \xrightarrow{P_1/P_0\rightarrow\infty} \frac{\gamma-1}{\gamma+1} .\end{align}

즉, 복사 우세기

\gamma=4/3

을 고려하면 원래 체적의 1/7까지 압축된다.

2. 3. 오일러 방정식으로부터의 유도

1차원 용기(예: 길고 얇은 튜브) 내의 기체를 가정하고, 유체가 비점성이며(점성 효과 무시), 열 전달(전도 또는 복사)이 없고, 중력을 무시할 수 있다고 가정한다. 이러한 시스템은 1차원 오일러 방정식으로 설명할 수 있다.^[7]

이 방정식들에서 사용되는 변수는 다음과 같다.

$\rho$ : 유체 질량 밀도
$u$ : 유체 속도
$e$ : 유체의 비내부 에너지
$p$ : 유체 압력
$E^t = \rho e + \rho\tfrac{1}{2}u^2$ : 유체의 총 에너지 밀도 [J/m³]

또한 기체가 열적으로 이상적이며, 다음과 같은 간단한 형태의 다변 상태 방정식이 유효하다고 가정한다.^[7]

:

p = \left(\gamma - 1\right)\rho e,

여기서

\gamma

는 비열비

c_p/c_v

의 상수이며, 다변 과정의 ''다변 지수''로도 나타난다.

:

\frac{p}{\rho^\gamma} = \text{constant}.

압축성 유동 방정식 등에 대한 자세한 내용은 NACA 보고서 1135 (1953)를 참조하면 된다.^[7]

열적으로 이상적인 기체의 경우

\gamma

는 상수이고, 열적으로 이상적인 기체의 경우

\gamma

는 온도의 함수이다.

충격파 속도는 다음과 같이 주어진다.^[7]

:

u_s = u_1 + c_1 \sqrt{1 + \frac{\gamma+1}{2\gamma} \left( \frac{p_2}{p_1} - 1\right)},

여기서

c_{1}=\sqrt{\gamma p_{1}/\rho_{1}}

는 상류 조건에서 유체의 음속이다.

2. 4. 고체에서의 충격파

고체에서의 충격은 실험적 관찰^[15]에 따라 다음과 같은 선형 관계^[16]를 사용한다(''u''_s-''u''_p 평면에서 충격 Hugoniot라고 함).

: ''u''_s = ''c''₀ + ''s'' ''u''_p = ''c''₀ + ''s'' ''u''₂

여기서 ''c''₀는 재료의 벌크 음속(일축 압축)이고, ''s''는 실험 데이터를 맞추어 얻은 매개변수(충격 Hugoniot의 기울기)이며, ''u''_p = ''u''₂는 충격 전선 뒤의 압축된 영역 내부의 입자 속도이다.

일부 재료에 대한 충격 Hugoniot ^[17]^[18]
재료	기호	ρ (kg/m³)	c_0 (m/s)	s	측정 압력 범위 (kbar)
은	Ag	10490kg/m3	3270m/s	1.55	200-1500
금	Au	19240kg/m3	3070m/s	1.54	255-1900
구리	Cu	8920kg/m3	3910m/s	1.51	80-3700

위의 관계는 질량 및 운동량 보존에 대한 Hugoniot 방정식과 결합될 때, ''p''-''v'' 평면에서 충격 Hugoniot을 결정하는 데 사용될 수 있으며, 여기서 ''v''는 비체적(단위 질량당)이다.^[19]

: ''p''₂ - ''p''₁ = (''c''₀² ρ₁ ρ₂ (ρ₂ - ρ₁)) / (ρ₂ - ''s''(ρ₂ - ρ₁))² = (''c''₀²(''v''₁ - ''v''₂)) / (''v''₁ - ''s''(''v''₁ - ''v''₂))²

Mie–Grüneisen 상태 방정식과 같은 대체 상태 방정식도 위의 방정식 대신 사용할 수 있다.

충격 Hugoniot은 충격 뒤에 재료가 존재할 수 있는 모든 가능한 열역학적 상태의 궤적을 2차원 상태 평면에 투영하여 설명한다. 따라서 평형 상태의 집합이며, 재료가 변형을 겪는 경로는 구체적으로 나타내지 않는다.

약한 충격은 등엔트로피이며 등엔트로피는 수렴하는 특성을 가진 압축파에 의해 초기 상태에서 최종 상태로 재료가 가해지는 경로를 나타낸다. 약한 충격의 경우, Hugoniot은 따라서 등엔트로피 위에 직접 떨어지며 동일한 경로로 직접 사용될 수 있다. 강한 충격의 경우, 우리는 더 이상 그 단순화를 직접적으로 할 수 없다. 그러나 공학적 계산을 위해, 등엔트로피가 Hugoniot에 충분히 가까워서 동일한 가정을 할 수 있다고 간주된다.

Hugoniot이 "등가" 압축파에 대한 상태 사이의 대략적인 로딩 경로인 경우, 충격 로딩 경로에 대한 점프 조건은 초기 상태와 최종 상태 사이의 직선을 그어 결정할 수 있다. 이 선을 레일리 선이라고 하며 다음 방정식을 갖는다.

: ''p''₂ - ''p''₁ = ''u''_s²(''ρ''₁ - (''ρ''₁²/''ρ''₂))

대부분의 고체 물질은 강한 충격을 받으면 소성 변형을 겪는다. 물질이 순수한 탄성 상태에서 탄성-소성 상태로 전환되는 충격 Hugoniot상의 점을 Hugoniot 탄성 한계(HEL)라고 하며, 이 전환이 일어나는 압력을 ''p''_HEL로 표시한다. ''p''_HEL 값은 0.2GPa에서 20GPa까지 다양할 수 있다. HEL 이상에서는 물질이 전단 강도의 대부분을 잃고 유체처럼 행동하기 시작한다.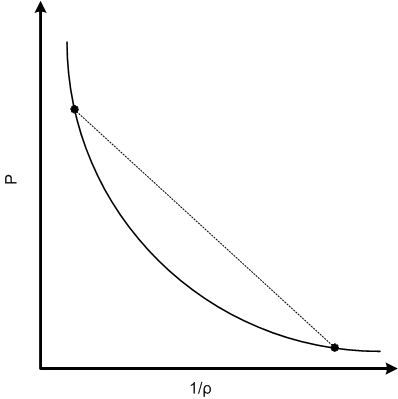

탄소성 재료의 충격에 대한 ''p''-''v'' 평면에서의 Hugoniot 탄성 한계.

2. 5. 자기유체역학 (Magnetohydrodynamics, MHD)

자기유체역학에서의 랭킨-위고니오 조건은 천체물리학적 적용과 매우 관련이 있기 때문에 고려할 가치가 있다. 불연속면을 가로질러 자기장

\mathbf H

의 수직 성분

H_n

과 전기장

\mathbf E = - \mathbf u \times \mathbf H/c

의 접선 성분

\mathbf E_t

(무한 전도율 한계)는 연속적이어야 한다.^[20]

따라서 다음이 성립한다.

:

\begin{align}0=[\![j]\!],\,\, j\equiv \rho u_n &\quad \text{질량 보존}, \\0=[\![H_n]\!] &\quad \text{자기장 }\mathbf H\text{의 수직 성분 연속성},\end{align}

여기서

[\![\cdot ]\!]

는 불연속면의 양쪽에서 임의의 물리량 값의 차이이다. 나머지 조건은 다음과 같다.

:

\begin{align}j^2[\![1/\rho]\!] + [\![p]\!] + [\![\mathbf H_t^2]\!]/8\pi = 0 &\quad \text{수직 운동량 보존},\\j[\![\mathbf u_t]\!] = H_n [\![\mathbf H_t]\!]/4\pi &\quad \text{접선 운동량 보존},\\j[\![h+j^2/2\rho^2+\mathbf u_t^2/2 + \mathbf H_t^2/4\pi\rho]\!] = H_n[\![\mathbf H_t\cdot\mathbf u_t]\!]/4\pi &\quad \text{에너지 보존},\\H_n[\![\mathbf u_t]\!] = j[\![\mathbf H_t/\rho]\!] &\quad \text{전기장 }\mathbf E\text{의 접선 성분 연속성}.\end{align}

이러한 조건은 접촉 불연속면(

j=0,\, H_n\neq 0, \,[\![\mathbf u]\!]=[\![\p]\!]=[\![\mathbf H]\!]=0,\, [\![\rho]\!]\neq 0

), 접선 불연속면(

j=H_n=0,\,[\![\mathbf u_t\rho]\!]\neq 0,\, [\![\mathbf H_t]\!]\neq 0,\,[\![\rho]\!]\neq 0

), 회전 또는 알벤 불연속면 (

j=H_n\sqrt{\rho/4\pi}\neq 0,\,[\![\rho]\!]=[\![\u_n]\!]=[\![\p]\!]=[\![\mathbf H_t]\!]=0

) 및 충격파(

j\neq 0,\,[\![\rho]\!]\neq 0

)를 포함한다는 점에서 일반적이다.

참조

_[1] 논문 On the thermodynamic theory of waves of finite longitudinal disturbances http://gallica.bnf.f[...]
_[2] 논문 Mémoire sur la propagation des mouvements dans les corps et spécialement dans les gaz parfaits (première partie) [Memoir on the propagation of movements in bodies, especially perfect gases (first part)] https://books.google[...]
_[3] 웹사이트 The Curious Events Leading to the Theory of Shock Waves, Invited lecture,'' 17th Shock Interaction Symposium'', Rome'','' 4–8 September. https://ntrs.nasa.go[...]
_[4] 서적 Combustion theory CRC Press
_[5] 논문 The normal velocity of ignition of combustible gaseous mixtures 1893
_[6] 서적 Physics of shock waves and high-temperature hydrodynamic phenomena Courier Corporation
_[7] 간행물 Equations, Tables and Charts for Compressible Flow https://www.grc.nasa[...]
_[8] 문서
_[9] 서적 Elements of gasdynamics Courier Corporation
_[10] 서적 EM Lifshitz, Fluid Mechanics Course of Theoretical Physics, 6
_[11] 서적 The dynamics and thermodynamics of compressible fluid flow John Wiley & Sons
_[12] 서적 Modern compressible flow: with historical perspective (Vol. 12) New York: McGraw-Hill
_[13] 서적 Linear and Nonlinear Waves Wiley
_[14] 서적 Supersonic flow and shock waves (Vol. 21) Springer Science & Business Media
_[15] 간행물 Equation of state http://www.fas.harva[...]
_[16] 문서
_[17] 보고서 User's manual for LASL shock Hugoniot data file http://dx.doi.org/10[...] Office of Scientific and Technical Information (OSTI) 1979-07-01
_[18] 서적 Shock Wave Compression of Condensed Matter: A Primer https://link.springe[...] Springer Berlin Heidelberg 2012
_[19] 서적 Introduction to the Physics of the Earth's Interior Cambridge University Press
_[20] 서적 Electrodynamics of continuous media elsevier
_[21] 서적 流体力学培風館
_[22] 서적 高速流体力学森北出版
_[23] 서적 Physics of the Interstellar and Intergalactic Medium https://ui.adsabs.ha[...] Princeton University Press

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com