맨위로가기

로렌즈 방정식

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

로렌즈 방정식은 1963년 에드워드 노턴 로렌즈가 발표한 3개의 변수를 갖는 비선형 상미분 방정식으로, 대류 현상을 모델링하기 위해 개발되었다. 이 방정식은 프란틀 수, 레일리 수와 관련된 매개변수를 포함하며, 특정 조건에서 혼돈적인 해를 보여 '로렌츠 끌개'라는 특이한 끌개를 갖는다. 로렌즈 방정식은 레이저, 발전기, 열사이펀 등 다양한 물리 시스템의 모델로 활용되며, 초기 조건에 대한 민감성으로 인해 혼돈 이론의 중요한 사례로 여겨진다.

더 읽어볼만한 페이지

  • 혼돈 이론 - 창발
    창발은 부분에는 없던 성질이 전체에서 나타나는 현상으로, 철학적으로는 요소의 속성으로 설명할 수 없는 체계의 특징을 의미하며, 복잡계 과학, 생명 현상 등 다양한 분야에서 중요한 개념으로 다뤄진다.
  • 혼돈 이론 - 난류 (역학)
    난류는 유체의 불규칙하고 무작위적인 운동 상태로, 일상생활과 공학 등 다양한 분야에서 관찰되며 여러 특징을 설명하기 위한 연구가 진행 중이다.
로렌즈 방정식
로렌즈 시스템
개요
유형상미분 방정식
차원3차원
방정식ẋ = σ(y - x)
ẏ = x(ρ - z) - y
ż = xy - βz
매개변수ρ (로)
σ (시그마)
β (베타)
고정점(0, 0, 0), (±√(β(ρ − 1)), ±√(β(ρ − 1)), ρ − 1)
카오스ρ > 24.74
설명
설명대류의 단순화된 수학적 모델
관련 항목
관련 항목나비 효과
카오스 이론
역학계
아트락토르

2. 정의

'''로렌즈 방정식'''은 ''x''(t), ''y''(t), ''z''(t) 세 변수에 대한 1차 비선형 연립 상미분 방정식이며, 세 개의 매개변수 σ, ρ, β에 의존한다. 로렌즈 방정식은 다음과 같다.

:\dot x=\sigma(y-x)

:\dot y=x(\rho-z)-y

:\dot z=xy-\beta z

로렌즈가 원래 논문[75]에서 사용한 매개변수 값은 σ = 10, β = 8/3, ρ = 28이다. 이 값에서 로렌즈 방정식은 혼돈적인 성질을 보이며, '''로렌즈 끌개'''라는 야릇한 끌개를 가진다.

1963년, 에드워드 로렌츠는 대기 대류에 대한 단순화된 수학적 모델을 개발했다.[2] 이 모델은 현재 로렌츠 방정식으로 알려진 세 개의 상미분 방정식 시스템으로, 아래에서 균일하게 가열되고 위에서 냉각되는 2차원 유체 층의 특성을 관련시킨다. 특히, 이 방정식들은 시간에 따른 세 가지 양의 변화율을 설명한다. ''x''는 대류율에 비례하고, ''y''는 수평 온도 변화에 비례하며, ''z''는 수직 온도 변화에 비례한다.[3] 상수 σ, ρ, 그리고 β는 프란틀 수, 레일리 수, 그리고 층 자체의 특정 물리적 차원에 비례하는 시스템 매개변수이다.[3]

3. 성질

로렌즈 방정식은 \((x, y, z) \mapsto (-x, -y, z)\)에 대한 대칭성을 가진다. σ ≠ 0이고 β(ρ - 1) > 0일 때, 다음과 같은 세 개의 평형점을 가진다.

:(x,y,z)=\left(\sqrt{\beta(\rho-1)},\sqrt{\beta(\rho-1)},(\rho-1)\right)

:(x,y,z)=\left(-\sqrt{\beta(\rho-1)},-\sqrt{\beta(\rho-1)},(\rho-1)\right)

:(x,y,z)=(0,0,0)

만약 σ ≠ 0이지만 β(ρ - 1) < 0일 경우, 마지막 하나의 평형점만이 존재한다.

z축 \(\{(0,0,z)\colon z\in\mathbb R\}\)은 불변 집합이다. z축 위에서 로렌즈 방정식은 \(\dot z=-\beta z\)가 되므로, β > 0이라면 이 경우 모든 초기 조건은 원점 (0,0,0)으로 지수적으로 수렴한다.

로렌즈 끌개는 3차원 속의 곡면 속에 존재하며, 프랙털 모양을 하고 있다.


매개변수 ρ의 값에 따라 분기(bifurcation)가 발생하며, 다양한 동역학적 성질을 보인다. 일반적으로 매개변수 σ, ρ, β는 양수라고 가정한다. 에드워드 로렌츠는 σ = 10, β = 8/3 및 ρ = 28 값을 사용했다. 이 시스템은 이러한 값(그리고 근처) 값에 대해 혼돈적인 동작을 보인다.[17]

만약 ρ < 1이라면, 평형점은 원점 단 하나뿐이다. 이 점은 대류가 없음을 나타낸다. 모든 궤도는 ρ < 1일 때, 전역적인 어트랙터인 원점에 수렴한다.[18]

ρ = 1에서 피치포크 분기가 발생하며, ρ > 1일 때 두 개의 추가적인 임계점이 다음과 같이 나타난다.

:\(\left( \sqrt{\beta(\rho-1)}, \sqrt{\beta(\rho-1)}, \rho-1 \right)\) and \(\left( -\sqrt{\beta(\rho-1)}, -\sqrt{\beta(\rho-1)}, \rho-1 \right)\).

이것들은 정상적인 대류에 해당한다. 이 두 개의 평형점은 \(\rho < \sigma\frac{\sigma+\beta+3}{\sigma-\beta-1}\) 의 경우에만 안정적이다. 이것은 σ > β + 1일 때만 ρ는 양수가 될 수 있다. 또한 임계값에서는, 두 평형점은 호프 분기를 거쳐 안정성을 잃는다.[19]

ρ = 28, σ = 10, β = 8/3일 때, 로렌츠 시스템은 혼돈적인 해를 갖는다(단 모든 해가 혼돈인 것은 아니다). 거의 모든 초기점은 세 개의 평형점에 관해 불변 집합, 즉 로렌츠 끌개, 스트레인지 끌개, 프랙탈, 자기 여기 끌개로 기울어지게 된다. 그 하우스도르프 차원은, 위에서 랴푸노프 지수에 의해 2.06 ± 0.01로 추정된다.[56] 또한 상관 차원은 2.05 ± 0.01로 추정된다.[57] 글로벌 끌개의 정확한 랴푸노프 지수의 공식은, 파라미터의 고전적인 제한 하에서 해석적으로 구할 수 있으며, \(\ 3 - \frac{2 (\sigma + \beta + 1)}{\sigma + 1 + \sqrt{\left(\sigma-1\right)^2 + 4 \sigma \rho}} \) 와 같다.[58][56][59]

로렌츠 끌개는 해석이 어렵지만, 미분 방정식의 끌개로의 작용은 꽤 단순한 기하학적 모델로 기술되며[60], 이 증명은 스메일의 문제의 14번째 문제였지만, 2002년에 워릭 터커에 의해 처음으로 해결되었다.[61]

ρ의 다른 값에서는, 계는 매듭이 있는 주기적인 궤도를 나타낸다. 예를 들어, ρ = 99.96에서는 T(3,2)(토러스 매듭)가 된다.

다른 ρ에 대한 로렌츠 방정식의 해의 예
Image:Lorenz Ro14 20 41 20-200px.pngImage:Lorenz Ro13-200px.png
(확대)(확대)
Image:Lorenz Ro15-200px.pngImage:Lorenz Ro28-200px.png
(확대)(확대)
작은 ρ에서는 계가 안정하여, 두 고정점 중, 어느 한 점의 끌개로 발전한다. ρ > 24.74에서는, 고정점은 척력이 되어, 궤도는 그들에 반발하여 매우 복잡한 형태가 된다.



초기값에 대한 민감성
시간 (확대)시간 (확대)시간 (확대)
Image:Lorenz caos1-175.pngImage:Lorenz caos2-175.pngImage:Lorenz caos3-175.png
ρ = 28, σ = 10, β = 8/3의 조건으로 생성된 이들 이미지는 두 궤적(파랑과 노랑)의 시간 발전을 나타낸다. 두 궤적의 초기값은 x 좌표만 10−5의 차이가 있다. 처음에는 두 궤적은 일치하는 것처럼 보이지만(파란색 위에서 노란색이 그려져 있기 때문에 노란색 궤적만 보인다), 시간이 지남에 따라 분명히 분기되는 것을 알 수 있다.



근접 궤적의 발산.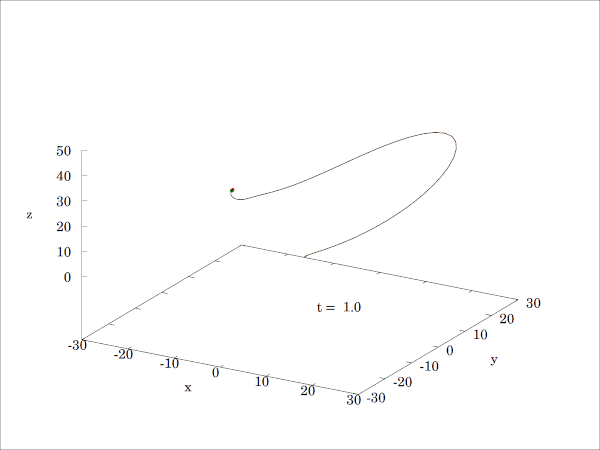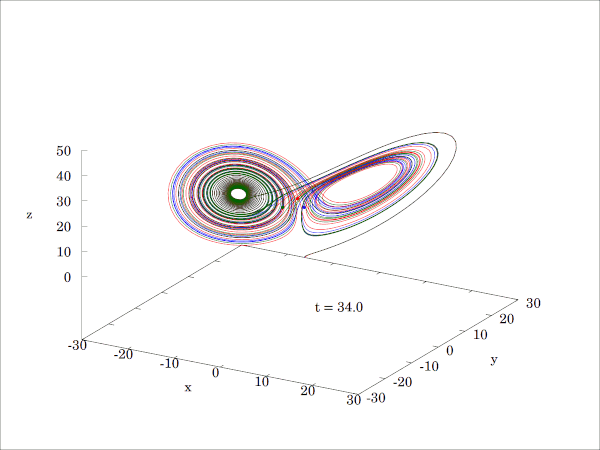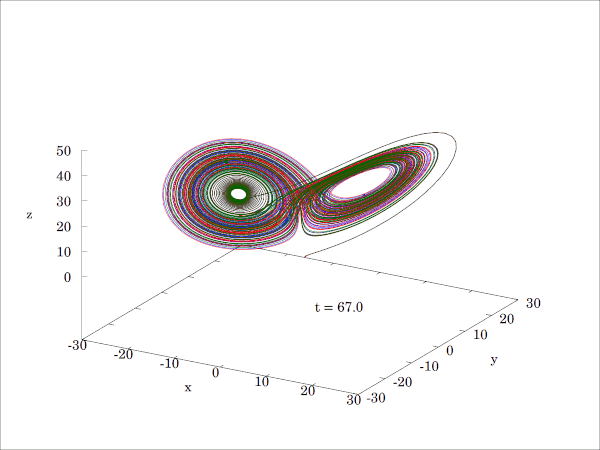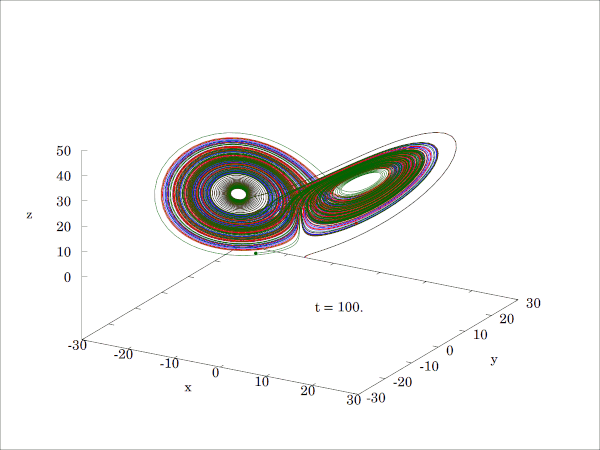
로렌츠 시스템의 세 개의 초기 근접 궤적의 진화. 이 애니메이션에서는 Runge-Kutta 루틴을 사용하여 방정식을 수치적으로 적분한다 — 세 개의 초기 조건 (0.9,0,0) (녹색), (1.0,0,0) (파란색) 및 (1.1,0,0) (빨간색)에서 시작하여 만들어짐. WxMaxima로 제작.
매개변수는 다음과 같다: ρ = 28, σ = 10 및 β = 8/3. 약 t = 24.0에서 상당한 발산이 보이며, 그 이후 궤적은 상관 관계가 없어진다. 전체 크기 그래픽은 [https://upload.wikimedia.org/wikipedia/commons/1/1d/Lorenz_diverging_trajectories.gif 여기]에서 접근할 수 있다.


3. 1. 분기

(\beta,\sigma)=(8/3,10)으로 고정하고, \rho의 값을 변화시키면, 로렌즈 방정식은 다음과 같은 성질을 보인다.

  • \rho\in(0,1)일 경우, 원점은 유일한 안정적 평형점이다. 모든 궤도는 원점으로 수렴한다.
  • \rho=1에서 갈퀴 분기가 일어나며, 원점은 세 개의 평형점으로 분기한다. 원점은 이제 불안정 평형점이 되지만, 나머지 두 평형점은 안정적이다. 1<\rho<1.346일 경우 거의 모든 초기 조건은 두 안정적 평형점으로 수렴한다.
  • \rho=1.346에서 호프 분기가 일어나며, 모든 평형점이 불안정해진다. 대신 두 개의 안정적인 극한 주기 궤도 C_+, C_-이 생기며, 1.346<\rho<13.926일 경우 거의 모든 초기 조건은 두 극한 주기 궤도 가운데 더 가까운 쪽으로 수렴한다.
  • 13.926<\rho<24.06일 경우, 로렌즈 방정식은 '''일시적 혼돈'''(transient chaos영어)을 보인다. 즉, 두 안정적 극한 주기 궤도 C_+, C_-가 존재하며 거의 모든 궤도는 이 둘 가운데 하나로 수렴하지만, 일부 초기 조건에 대하여 어느 쪽으로 수렴하는지 여부는 초기 조건에 대하여 민감하게 의존한다.
  • 24.06<\rho<24.74일 경우, 로렌즈 방정식은 일부 초기 조건에 대하여 혼돈을 보이기 시작한다. 그러나 두 극한 주기 궤도 C_\pm는 여전히 안정적이다.
  • \rho>\sigma\tfrac{\sigma+\beta+3}{\sigma-\beta-1}\approx24.74이면 두 극한 주기 궤도는 더 이상 안정적이지 않으며, 거의 모든 초기 조건에 대하여 혼돈이 발생한다.
  • * 특히, 로렌즈가 연구한 경우인 \rho=28인 경우는 혼돈적이다.
  • * 그러나 \rho>24.74인 경우에도, 특수한 \rho의 값에서는 혼돈이 발생하지 않을 수 있다.
  • 매우 큰 \rho의 값에 대하여 로렌즈 방정식은 다시 비혼돈적이게 된다. 구체적으로, \rho>313일 경우 거의 모든 궤도는 극한 주기 궤도로 수렴하게 된다.

4. 해석

일반적으로 매개변수 , , 는 양수라고 가정한다. 로렌츠는 , , 값을 사용했고, 이 시스템은 이러한 값과 그 근처의 값에 대해 혼돈스러운 동작을 보였다.[17]

만약 이면, 평형점은 원점 단 하나뿐이다. 이 점은 대류가 없음을 나타낸다. 모든 궤도는 일 때, 전역적인 어트랙터인 원점에 수렴한다.[18]

피치포크 분기는 에서 발생하며, 일 때 두 개의 추가적인 임계점이 다음과 같이 나타난다.

:\left( \sqrt{\beta(\rho-1)}, \sqrt{\beta(\rho-1)}, \rho-1 \right) \quad\text{and}\quad \left( -\sqrt{\beta(\rho-1)}, -\sqrt{\beta(\rho-1)}, \rho-1 \right).

이것들은 정상적인 대류에 해당한다. 이 평형점 쌍은 다음 조건을 만족할 경우에만 안정하다.

:\rho < \sigma\frac{\sigma+\beta+3}{\sigma-\beta-1},

이는 일 경우에만 양수 에 대해 성립할 수 있다. 임계값에서 두 평형점은 아임계 호프 분기를 통해 안정성을 잃는다.[19]

, , 일 때, 로렌츠 시스템은 혼돈적인 해를 갖는다(그러나 모든 해가 혼돈적인 것은 아니다). 거의 모든 초기점은 불변 집합인 로렌츠 어트랙터—세 평형점 모두에 관한 스트레인지 어트랙터, 프랙탈, 자기 여기 어트랙터—로 수렴하는 경향을 보인다. 이의 하우스도르프 차원은 리야푸노프 차원(Kaplan-Yorke 차원)에 의해 로 상한이 추정되며,[20] 상관 차원은 로 추정된다.[21] 전역 어트랙터의 정확한 리야푸노프 차원 공식은 매개변수에 대한 고전적인 제약 하에서 해석적으로 찾을 수 있다:[22][20][23]

: 3 - \frac{2 (\sigma + \beta + 1)}{\sigma + 1 + \sqrt{\left(\sigma-1\right)^2 + 4 \sigma \rho}}

로렌츠 어트랙터는 분석하기 어렵지만, 어트랙터에 대한 미분 방정식의 작용은 비교적 간단한 기하학적 모델로 설명된다.[24] 이것이 실제로 그러한 경우임을 증명하는 것은 Smale의 문제 목록의 열네 번째 문제였다. 이 문제는 2002년 워윅 터커에 의해 처음으로 해결되었다.[25]

다른 값에 대해, 시스템은 꼬인 주기적 궤도를 나타낸다. 예를 들어, 에서는 토러스 매듭이 된다.

다양한 값에 대한 로렌츠 시스템의 예시 해
----
----
----
----
작은 값의 경우, 시스템은 안정적이며 두 개의 고정점 어트랙터 중 하나로 진화한다. 일 때, 고정점은 반발점이 되며 궤도는 매우 복잡한 방식으로 이들에 의해 튕겨져 나간다.



초기 조건에 대한 민감한 의존성
시간 --시간 --시간 --
이 그림들은 — , , 을 사용하여 만들어졌으며 — 로렌츠 어트랙터에서 좌표에서 10−5만 다른 두 초기점에서 시작하는 두 궤적(하나는 파란색, 다른 하나는 노란색)의 3차원 진화를 세 개의 시간 구간으로 보여준다. 처음에 두 궤적은 일치하는 것처럼 보이지만(노란색 궤적이 파란색 궤적 위에 그려져 있으므로 노란색 궤적만 볼 수 있다) 일정 시간이 지나면 발산이 분명해진다.



근접 궤적의 발산.
로렌츠 시스템의 세 개의 초기 근접 궤적의 진화. 이 애니메이션에서는 Runge-Kutta 루틴을 사용하여 방정식을 수치적으로 적분한다. 세 개의 초기 조건 (녹색), (파란색) 및 (빨간색)에서 시작하여 만들어졌다. WxMaxima로 제작.
매개변수는 다음과 같다: , , . 약 에서 상당한 발산이 보이며, 그 이후 궤적은 상관 관계가 없어진다. 전체 크기 그래픽은 [https://upload.wikimedia.org/wikipedia/commons/1/1d/Lorenz_diverging_trajectories.gif 여기]에서 접근할 수 있다.



스메일의 14번째 문제는 '로렌츠 끌개의 속성은 이상한 끌개의 속성을 나타내는가?'였다. 이 문제는 2002년 워윅 터커에 의해 긍정적으로 해결되었다.[25] 이 결과를 증명하기 위해 터커는 구간 산술과 정규형과 같은 엄격한 수치적 방법을 사용했다. 먼저, 터커는 흐름 궤도에 의해 가로지르는 단면 을 정의했다. 이것으로부터, 각 에 의 궤도가 처음으로 와 교차하는 점 를 할당하는 첫 번째 반환 맵 를 정의할 수 있다.

그다음 증명은 이상한 끌개의 존재를 함축하는 세 가지 주요 점으로 나뉜다.[39] 세 가지 점은 다음과 같다.


  • 첫 번째 반환 맵 아래에서 불변인 영역 가 존재한다. 즉, 이다.
  • 반환 맵은 순방향 불변 원뿔장을 허용한다.
  • 이 불변 원뿔장 내부의 벡터는 반환 맵의 미분 에 의해 균일하게 확장된다.


첫 번째 점을 증명하기 위해, 단면 가 에 의해 형성된 두 개의 호에 의해 잘린다는 것을 알 수 있다.[39] 터커는 이 두 호의 위치를 작은 직사각형 로 덮고, 이 직사각형들의 합집합이 을 제공한다. 이제 목표는 의 모든 점에 대해 흐름이 의 점을 으로 되돌려 보낸다는 것을 증명하는 것이다. 이를 위해, 우리는 아래 만큼 떨어진 거리에 있는 평면 을 취하고, 의 중심 를 취하여 오일러 적분법을 사용하여 흐름이 를 로 가져갈 위치를 추정할 수 있으며, 이는 새로운 점 을 제공한다. 그런 다음, 테일러 전개를 사용하여 의 점이 로 매핑될 위치를 추정할 수 있으며, 이는 를 중심으로 하는 새로운 직사각형 을 제공한다. 따라서 우리는 의 모든 점이 로 매핑될 것임을 알고 있다. 목표는 흐름이 로 되돌아올 때까지 이 방법을 재귀적으로 적용하여 임을 아는 직사각형 를 에서 얻는 것이다. 문제는 몇 번의 반복 후에 우리의 추정이 부정확해질 수 있다는 것이다. 따라서 터커가 하는 일은 를 더 작은 직사각형 로 분할한 다음 프로세스를 재귀적으로 적용하는 것이다.

또 다른 문제는 이 알고리즘을 적용할 때 흐름이 더 '수평적'이 되어[39] 부정확성이 극적으로 증가한다는 것이다. 이를 방지하기 위해 알고리즘은 단면의 방향을 변경하여 수평 또는 수직이 되도록 한다.

5. 텐트 사상과의 관련성

Mathematica로 생성된 로렌츠 결과 재현. 빨간색 선 위의 점들은 시스템이 로브를 전환하는 것에 해당한다.


로렌츠는 자신의 논문[2] 그림 4에서, 시스템이 z 방향으로 얻는 상대 최댓값을 이전 z 방향의 상대 최댓값에 대해 그렸다. 이 방법은 나중에 로렌츠 맵(궤적과 지정된 표면의 교차점을 그리는 푸앵카레 플롯과 혼동하지 말 것)으로 알려지게 되었다. 그 결과는 텐트 맵과 매우 유사한 형태를 보였다. 로렌츠는 또한 최대 z 값이 특정 컷오프 이상일 때 시스템이 다음 로브로 전환된다는 것을 발견했다. 이것을 텐트 맵에 의해 나타나는 것으로 알려진 혼돈과 결합하여, 그는 시스템이 두 로브 사이를 혼돈스럽게 전환한다는 것을 보였다.[42]

6. 일반화된 로렌츠 방정식

지난 수년간 고차원 로렌츠 모델에 관한 연구를 통해 일반화된 로렌츠 모델이 도출되었다.[26] 이 모델은 세 개의 상태 변수를 갖는 고전적인 로렌츠 모델 또는 다섯 개의 상태 변수를 갖는 아래의 5차원 로렌츠 모델로 단순화될 수 있다.[27]

: \begin{align}

\frac{\mathrm{d}x}{\mathrm{d}t} &= \sigma (y - x), \\[6pt]

\frac{\mathrm{d}y}{\mathrm{d}t} &= x (\rho - z) - y, \\[6pt]

\frac{\mathrm{d}z}{\mathrm{d}t} &= x y - x y_1 - \beta z, \\[6pt]

\frac{\mathrm{d}y_1}{\mathrm{d}t} &= x z - 2 x z_1 - d_0 y_1, \\[6pt]

\frac{\mathrm{d}z_1}{\mathrm{d}t} &= 2 x y_1 - 4\beta z_1.

\end{align}

다른 매개변수 선택과의 일관성을 위해 d_0=\dfrac{19}{3}가 사용되었다.[26][27]

7. 응용

로렌츠의 카오스 모델 개척 기여에서 볼 수 있듯이, 1963년 에드워드 로렌츠는 대기 대류에 대한 단순화된 수학적 모델을 개발했다.[2] 이 모델은 현재 로렌츠 방정식으로 알려진 세 개의 상미분 방정식 시스템이다.

로렌츠 방정식은 레이저,[4] 다이너모,[5] 열사이펀,[6] 브러시리스 직류 전동기,[7] 전기 회로,[8] 화학 반응[9] 및 순방향 삼투[10]에 대한 단순화된 모델에서 발생할 수 있다. 1975년 하켄은 1963년에 유도된 방정식이 원래의 로렌츠 방정식과 수학적으로 동등하다는 것을 깨달았다.[12] 따라서 하켄의 논문은 레이저 카오스 또는 광학 카오스라는 새로운 분야를 시작했고, 로렌츠 방정식은 광학 문헌에서 종종 로렌츠-하켄 방정식이라고 불린다. 이후 로렌츠 방정식의 복소수 버전도 레이저와 등가임이 밝혀졌다.[14]

로렌츠 방정식은 맬커스 워터휠에 대한 푸리에 공간에서 지배 방정식이기도 하다.[15][16] 맬커스 워터휠은 한 방향으로 회전하는 대신 회전 속도가 빨라지고, 느려지고, 멈추고, 방향을 바꾸는 등 예측할 수 없는 카오스적인 운동을 보인다.

기술적인 관점에서 로렌츠 시스템은 비선형, 비주기적, 3차원 및 결정론적이다. 로렌츠 방정식은 수백 편의 연구 논문의 주제였으며, 최소 한 권의 책 분량의 연구가 이루어졌다.[3]

7. 1. 대기 대류 모델

로렌즈 방정식은 배리 솔츠먼이 연구한 더 큰 시스템의 축소된 버전이다.[28][29] 이 방정식은 아래에서 균일하게 가열되고 위에서 균일하게 냉각되는 얕은 유체층에서 유체 순환을 설명하는 방정식에 대한 오버벡-부시네스크 근사에서 유도된다.[30] 이러한 유체 순환은 레일리-베나르 대류로 알려져 있으며, 유체는 주기적인 직사각형 경계 조건을 갖는 2차원(수직 및 수평)으로 순환한다고 가정한다.[31]

시스템의 유선 함수와 온도를 모델링하는 편미분 방정식은 스펙트럼 갈레르킨 근사를 거친다. 유체역학적 필드는 푸리에 급수로 전개되는데, 이는 유선 함수에 대한 단일 항과 온도에 대한 두 개의 항으로 심하게 잘린다. 이로 인해 모델 방정식은 세 개의 결합된 비선형 상미분 방정식 집합으로 축소된다.

7. 2. 대기 중 카오스와 질서의 성질을 나타내는 모델

과학계는 저차원 로렌츠 모델에서 발견되는 혼돈적 특징이 지구 대기의 특징을 나타낼 수 있다는 점을 받아들이고 있으며([33][34][35]), 이는 "날씨는 혼돈적이다"라는 명제로 이어진다. 이와 비교하여, 일반화된 로렌츠 모델([26])과 원래 로렌츠 모델([36][37]) 내의 끌개 공존 개념을 바탕으로, 션과 그의 공동 연구자들은([35][38]) "날씨는 뚜렷한 예측 가능성을 가진 혼돈과 질서를 모두 가지고 있다"는 수정된 견해를 제시했다. 이러한 수정된 견해는 기존 견해의 발전으로, "이론적 로렌츠 모델에서 발견되는 혼돈적이고 규칙적인 특징이 지구 대기의 특징을 더 잘 나타낼 수 있다"는 점을 시사한다.

8. 시뮬레이션

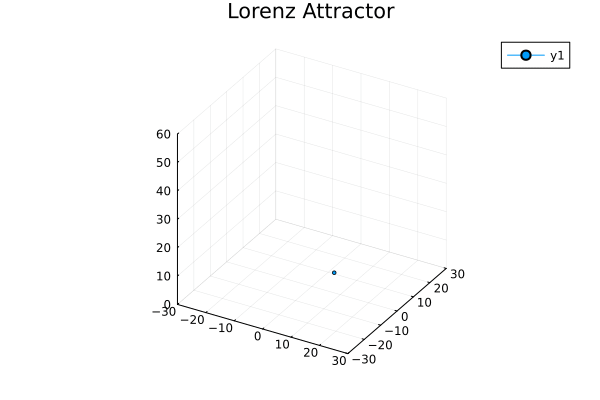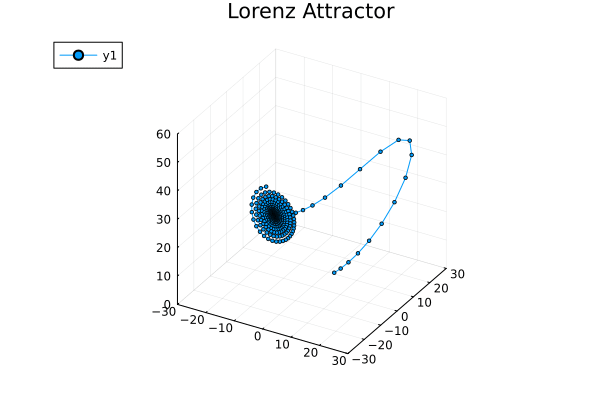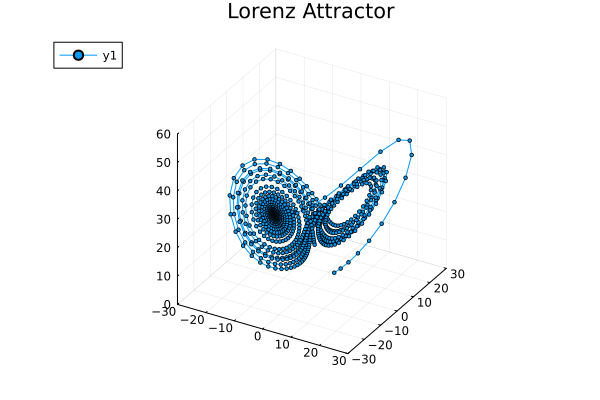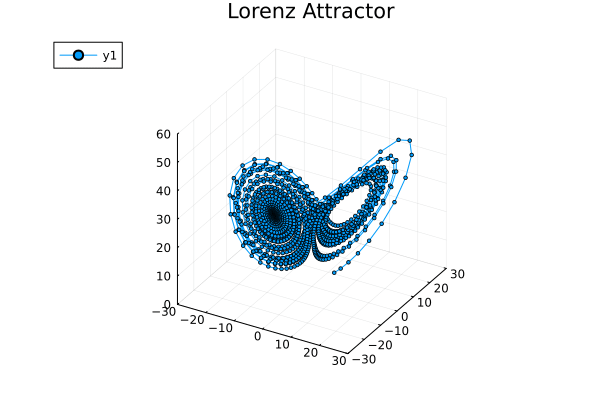
Julia에서 로렌츠 시스템 시뮬레이션
줄리아 시뮬레이션


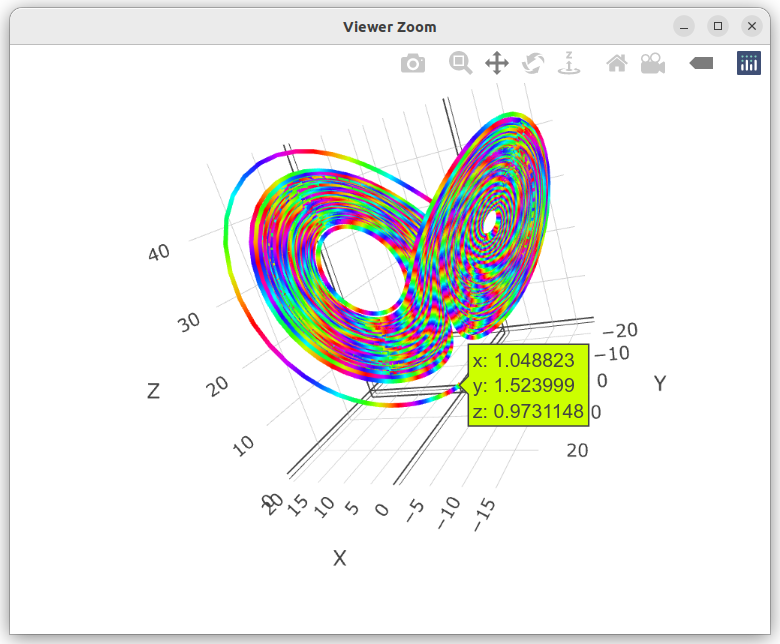
Lorenz System simulation in R
R 시뮬레이션


다양한 프로그래밍 언어(Julia, Maple, Maxima, MATLAB, Mathematica, Python, R 등)를 사용하여 로렌츠 방정식의 해를 시뮬레이션하고 시각화할 수 있다.

9. 역사

1963년 미국의 기상학자인 에드워드 노턴 로렌즈가 〈결정론적 비주기 흐름〉(Deterministic nonperiodic flow영어)이라는 논문에서 이 방정식을 발표하였다.[75] 로렌즈 방정식은 프랑스 물리학자 앙리 베나르와 영국 물리학자 존 윌리엄 스트럿 레일리의 이론을 기초로 유도되었다. 이 방정식에서 초기 조건에 대한 민감성이 발견되면서 혼돈 이론의 시초로 여겨진다.

엘렌 페터와 마거릿 해밀턴은 수치 시뮬레이션 및 계산을 담당하여 로렌츠 방정식 발견에 기여하였다.[1][2]

참조

[1] harvtxt
[2] harvtxt
[3] harvtxt
[4] harvtxt
[5] harvtxt
[6] harvtxt
[7] harvtxt
[8] harvtxt
[9] harvtxt
[10] harvtxt
[11] 간행물 Nonlinear Interaction of Laser Modes
[12] harvtxt
[13] harvtxt
[14] 간행물 Detuned lasers and the complex Lorenz equations: Subcritical and supercritical Hopf bifurcations
[15] harvtxt
[16] harvtxt
[17] harvtxt
[18] harvtxt
[19] harvtxt
[20] 간행물 The Lorenz system: hidden boundary of practical stability and the Lyapunov dimension
[21] harvtxt
[22] harvtxt
[23] 서적 Attractor Dimension Estimates for Dynamical Systems: Theory and Computation https://www.springer[...] Springer
[24] 간행물 Structural stability of Lorenz attractors http://www.numdam.or[...] 1979-12-01
[25] harvtxt
[26] 간행물 Aggregated Negative Feedback in a Generalized Lorenz Model 2019-03-01
[27] 간행물 Nonlinear Feedback in a Five-Dimensional Lorenz Model http://dx.doi.org/10[...] 2014-04-28
[28] harvtxt
[29] harvtxt
[30] harvtxt
[31] harvtxt
[32] 간행물 Nonlinear feedback in a six-dimensional Lorenz model: impact of an additional heating term https://npg.copernic[...] 2015-12-21
[33] 간행물 Geophysical flows as dynamical systems: the influence of Hide's experiments http://dx.doi.org/10[...] 2010-07-23
[34] 서적 Application of Chaos to Meteorology and Climate. In The Nature of Chaos; Mullin, T., Ed Oxford Science Publications
[35] 간행물 The Dual Nature of Chaos and Order in the Atmosphere 2022-11-12
[36] 논문 Metastable chaos: The transition to sustained chaotic behavior in the Lorenz model https://doi.org/10.1[...] 1979-09-01
[37] 간행물 Is Weather Chaotic? Coexisting Chaotic and Non-chaotic Attractors within Lorenz Models https://link.springe[...] Springer International Publishing 2022-12-22
[38] 논문 Is Weather Chaotic?: Coexistence of Chaos and Order within a Generalized Lorenz Model 2021-01-01
[39] 문서 Viana 2000
[40] 웹사이트 Brain Dynamics Toolbox https://bdtoolbox.or[...] 2017-2022
[41] 문서 Lorenz 1960
[42] 문서 Lorenz 1963
[43] 문서 Sparrow 1982
[44] 문서 Haken 1975
[45] 문서 Knobloch 1981
[46] 문서 Gorman, Widmann, Robbins 1986
[47] 문서 Hemati 1994
[48] 문서 Cuomo, Oppenheim 1993
[49] 문서 Poland 1993
[50] 문서 Tzenov 2014
[51] 문서 Kolář, Gumbs 1992
[52] 문서 Mishra, Sanghi 2006
[53] 서적 Hirsch, Smale, Devaney 2003
[54] 서적 Hirsch, Smale, Devaney 2003
[55] 서적 Hirsch, Smale, Devaney 2003
[56] 논문 The Lorenz system: hidden boundary of practical stability and the Lyapunov dimension
[57] 문서 Grassberger, Procaccia 1983
[58] 문서 Leonov, Kuznetsov, Korzhemanova, Kusakin 2016
[59] 서적 Attractor Dimension Estimates for Dynamical Systems: Theory and Computation https://www.springer[...] Springer
[60] 논문 Structural stability of Lorenz attractors http://www.numdam.or[...] 1979-12-01
[61] 문서 Tucker 2002
[62] 논문 Aggregated Negative Feedback in a Generalized Lorenz Model https://www.worldsci[...] 2019-03-01
[63] 논문 Nonlinear Feedback in a Five-Dimensional Lorenz Model https://doi.org/10.1[...] 2014-04-28
[64] 문서 Lorenz 1963
[65] 문서 Saltzman 1962
[66] 논문 Nonlinear feedback in a six-dimensional Lorenz model: impact of an additional heating term https://npg.copernic[...] 2015-12-21
[67] 논문 Geophysical flows as dynamical systems: the influence of Hide's experiments https://doi.org/10.1[...] 2010-07-23
[68] 서적 Application of Chaos to Meteorology and Climate. In The Nature of Chaos; Mullin, T., Ed Oxford Science Publications
[69] 논문 The Dual Nature of Chaos and Order in the Atmosphere 2022-11-12
[70] 논문 Metastable chaos: The transition to sustained chaotic behavior in the Lorenz model https://doi.org/10.1[...] 1979-09-01
[71] 간행물 Is Weather Chaotic? Coexisting Chaotic and Non-chaotic Attractors Within Lorenz Models https://link.springe[...] Springer International Publishing 2022-12-22
[72] 논문 Is Weather Chaotic?: Coexistence of Chaos and Order within a Generalized Lorenz Model https://journals.ame[...] 2021-01-01
[73] 문서 Viana 2000
[74] 웹사이트 Brain Dynamics Toolbox https://bdtoolbox.or[...] 2017-2022
[75] 저널 Deterministic nonperiodic flow 1963-03


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com