극한 주기 궤도

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 성질
- 3.1. 안정성
4. 존재 조건
5. 분기
6. 구체적인 예
7. 실제 현상
참조

1. 개요

극한 주기 궤도는 동역학계에서 나타나는 궤도의 일종으로, 궤도가 폐궤도는 아니지만, 궤도의 ω 극한 집합 또는 α 극한 집합이 폐궤도인 경우를 의미한다. 안정, 불안정, 반안정 극한 주기 궤도로 분류되며, 안정 극한 주기 궤도는 끌개의 한 예시이다. 2차원 연속 역학계에서 리미트 사이클은 고립된 폐궤도가 된다. 극한 주기 궤도는 비선형 계에서만 발생하며, 산일계에서 존재한다. 푸앵카레 사상과 리야푸노프 지수를 통해 안정성을 판별할 수 있으며, 호프 분기, 주기 배가 분기 등과 같은 분기 현상을 보인다. 극한 주기 궤도는 자가 진동하는 시스템을 모델링하는 데 중요한 역할을 하며, 공기역학, 신경 세포, 전기 회로, 생체 시계 등 다양한 실제 현상에 적용된다. 자려 진동 현상의 수리 모델이 될 수 있으며, 외란에도 안정적인 진동을 유지하는 특성을 갖는다.

더 읽어볼만한 페이지

비선형계 - 분기 (동역학계)
분기는 동역학계에서 매개변수 변화에 따라 평형점, 주기 궤도 등의 질적 변화가 발생하는 현상이며, 국소적 분기와 대역적 분기로 나뉜다.
비선형계 - 이력 현상
이력 현상은 입력 변화에 대한 시스템의 반응이 과거 상태에 의존하는 현상으로, 공학, 생물학, 경제학 등 다양한 분야에서 나타나며 자기 이력 현상은 정보 저장 매체에 활용되고 에너지 손실을 발생시키기도 한다.
극한 집합 - 안정성 이론
안정성 이론은 미분 방정식과 동역학적 시스템의 해의 점근적 성질과 궤적을 다루며, 평형점, 주기 궤도의 안정성, 섭동과 선형화, 랴푸노프 함수 등을 사용하여 시스템의 안정성을 분석한다.
극한 집합 - 끌개
끌개는 시간의 흐름에 따라 접근하는 상태 공간의 부분 공간으로, 시스템의 장기적인 거동을 결정하며, 파라미터 변화에 따라 분기 현상을 겪고 카오스적인 비선형 신호 분석에 활용된다.
동역학계 - 가상일
가상일은 역학계에서 외력이 가상 변위에 대해 하는 일의 합으로, 정역학에서는 계의 정적 평형 조건으로 활용되며, 달랑베르 원리를 통해 동역학에도 적용되어 구조 해석 및 계산에 널리 쓰이는 물리량이다.
동역학계 - 위상 공간 (물리학)
위상 공간은 역학계의 모든 가능한 상태를 모아 시스템의 상태 변수를 좌표로 나타낸 공간으로, 시간의 흐름에 따라 궤적을 그리며 시스템의 동역학적 거동을 분석하는 데 사용된다.

극한 주기 궤도
일반 정보
정의	비선형 동역학계에서 궤적이 시간이 지남에 따라 스스로 나선형으로 접근하는 고립된 주기 궤도
관련 분야	동역학계, 카오스 이론
수학적 정의
안정 극한 주기	초기 조건이 극한 주기에 충분히 가까운 궤적은 시간이 무한대로 갈 때 점근적으로 극한 주기에 접근함
불안정 극한 주기	초기 조건이 극한 주기에 가까워도 극한 주기에서 멀어짐
반안정 극한 주기	한쪽 방향에서는 안정하고 다른 방향에서는 불안정함
예시
진자 시계	일정 시간이 지나면 거의 같은 주기로 움직임
생물학적 시스템	신경 세포의 발화 패턴, 심장 세포의 박동
추가 정보
푸앵카레-벤딕손 정리	평면 상에서 해가 유계되어 있다면 극한 주기가 존재함

2. 정의

위상 공간 $X$ 위의 연속 시간 동역학계에서, 초기 조건 $x\in X$ 의 '''궤도'''는 다음과 같은 꼴의 집합이다.

: $\gamma(x)=\{\phi(t,x)\colon t\in\mathbb R\}$

이 동역학계의 '''주기 궤도'''는 다음 조건을 만족시키는 초기 조건 $x$ 에 대한 궤도이다.

: $\exists t\ne0\colon\phi(t,x)=x$

'''극한 주기 궤도'''는 다음 조건을 만족시키는 주기 궤도 $\gamma(x)$ 이다.

$\omega_\pm(y)=\gamma(x)$ 가 되는 $y\in X\setminus\gamma(x)$ 가 존재한다.

여기서

\omega_\pm

은 안정 또는 불안정 극한 집합이다.

극한 주기 궤도

\gamma(x)

에 대하여, 다음 조건을 만족시키는 근방

U\supset\gamma(x)

이 존재한다면,

\gamma(x)

를 '''안정 극한 주기 궤도'''라고 한다.

모든 $y\in U$ 에 대하여, $\omega_+(y)=\gamma(x)$

극한 주기 궤도

\gamma(x)

에 대하여, 다음 조건을 만족시키는 근방

U\supset\gamma(x)

이 존재한다면,

\gamma(x)

를 '''불안정 극한 주기 궤도'''라고 한다.

모든 $y\in U$ 에 대하여, $\omega_-(y)=\gamma(x)$

그러나 안정 극한 주기 궤도도, 불안정 극한 주기 궤도도 아닌 극한 주기 궤도가 존재한다. 안정 극한 주기 궤도는 끌개의 예이다.

2차원 연속 역학계에서, 상태 변수를

X = (x_1, x_2, \cdots, x_n) \in \mathbb{R}^n

라고 하면, 어떤 해

X(t)

가 평형해가 아니고,

X(t) = X(t+T)

를 만족하는

T>0

가 존재할 때,

X(t)

는 '''주기해'''라고 불린다. 특히

X(t) = X(t+T)

를 만족하는 최소의

T

는 '''주기'''라고 불린다.

시간

t

가

-\infty

에서

\infty

까지 변할 때 해

X(t)

가 가지는 상의 집합을 궤도라고 부른다. 주기해가 그리는 궤도는 '''폐궤도''' 또는 '''주기 궤도'''라고 불린다.

'''리미트 사이클'''은 다음과 같이 정의된다. 어떤 초기값

X_0 = X(0)

의 해를

\phi(t, X_0)

로 나타낸다고 하자. 상공간 상에 있는 폐궤도

C

가 존재한다고 하자.

C

의 어떤 근방

U

가 존재하고,

U

상의 임의의 점을 초기값으로 하는

\phi(t, X_0)

가

t \to \infty

또는

t \to -\infty

에서

C

에 점근할 때,

C

는 리미트 사이클이라고 불린다.

바꿔 말하면,

d(\phi(t, X_0), C)

를 점

\phi(t, X_0)

와 집합

C

내의

\phi(t, X_0)

에 가장 가까운 점 사이의 거리로 정의할 때,

:

\lim_{t \to \infty} d(\phi(t, X_0),C)=0

또는

:

\lim_{t \to -\infty} d(\phi(t, X_0),C)=0

가 되는

C

와

X_0 \notin C

가 존재할 때,

C

는 리미트 사이클이라고 불린다.

"리미트"는 극점 집합을 의미하며, 리미트 사이클은 '''극점 폐궤도'''^[11], '''극점 주기 궤도''', '''극점 사이클''' 등으로도 불린다.

극점 집합에는

t \to \infty

방향의

\omega

극점 집합과

t \to -\infty

방향의

\alpha

극점 집합의 2가지가 있다. 극점 집합을 사용하여 리미트 사이클을 정의하면 다음과 같다. 어떤 초기값

X_0

의 궤도는 폐궤도가 아니라고 하자. 그러나, 그 초기값

X_0

의

\omega

극점 집합

\omega(X_0)

또는

\alpha

극점 집합

\alpha(X_0)

이 폐궤도라고 하자. 이 때,

\omega(X_0)

또는

\alpha(X_0)

는 리미트 사이클이라고 불린다.

2차원 연속 역학계에서는, 상 평면상에서 리미트 사이클은 반드시 고립된 폐궤도가 된다. 즉, 리미트 사이클이 되는 폐궤도

C

의 근방에는 다른 폐궤도는 존재할 수 없다.

주위의 궤도를 흡인하는 리미트 사이클은 '''점근 안정''' 또는 단순히 '''안정'''이라고 한다. 안정인 리미트 사이클은 끌개의 1종류이다. 안정인 리미트 사이클을 '''주기 끌개'''라고도 한다^[13] .

주위의 궤도를 반발하는 리미트 사이클은 궤도 불안정 또는 단순히 '''불안정'''이라고 한다. 상 평면의 리미트 사이클로, 안쪽의 궤도가 흡인되고 바깥쪽의 궤도가 반발하는 경우, 또는 안쪽의 궤도가 반발하고 바깥쪽의 궤도가 흡인되는 경우, 이러한 경우의 리미트 사이클은 '''반안정'''이라고 한다^[14] .

3. 성질

요르단 곡선 정리에 따르면, 모든 닫힌 궤도는 평면을 곡선의 내부와 외부 두 영역으로 나눈다. 극한 주기 궤도에 접근하는 내부 또는 외부 궤도가 존재하면, 극한 주기 궤도 주변에는 시간이 무한대로 갈 때 극한 주기 궤도에서 시작하는 모든 궤도가 접근하는 이웃이 존재한다.^[11]

2차원 연속 역학계에서, 극한 주기 궤도는 상 평면상에서 반드시 고립된 폐궤도가 된다. 즉, 극한 주기 궤도가 되는 폐궤도 근방에는 다른 폐궤도가 존재할 수 없다. 근방 내의 모든 궤도는 그 궤도에 흡인되도록 접근하거나, 반발하여 멀어지는 두 가지 경우밖에 없다.^[12]

3. 1. 안정성

위상 공간 위의 연속 시간 동역학계에서, 극한 주기 궤도는 어떤 점 y가 존재하여 y의 안정 극한 집합 또는 불안정 극한 집합이 주기 궤도 γ(x)가 되는 경우를 말한다. (

\omega_\pm(y)=\gamma(x)

,

y\in X\setminus\gamma(x)

)^[11]

극한 주기 궤도

\gamma(x)

의 근방

U\supset\gamma(x)

안의 모든 점 y에 대해, y의 안정 극한 집합이

\gamma(x)

이면,

\gamma(x)

를 '''안정 극한 주기 궤도'''(stable limit cycle^영어)라고 한다. (

\omega_+(y)=\gamma(x)

)

반대로,

U\supset\gamma(x)

안의 모든 점 y에 대해, y의 불안정 극한 집합이

\gamma(x)

이면,

\gamma(x)

를 '''불안정 극한 주기 궤도'''(unstable limit cycle^영어)라고 한다. (

\omega_-(y)=\gamma(x)

)

안정 극한 주기 궤도는 끌개의 한 예로, 자체적으로 유지되는 진동을 나타낸다. 닫힌 궤도는 시스템의 완벽한 주기적 거동을 설명하며, 이 궤도에서 약간 벗어나더라도 시스템은 다시 궤도로 돌아와 극한 주기 궤도에 머무르게 된다.

모든 인접한 궤도가 시간이 무한대로 갈 때 극한 주기 궤도에 접근하면 ''안정'' (ω-극한 주기 궤도), 시간이 음의 무한대로 갈 때 접근하면 ''불안정'' (α-극한 주기 궤도)이라고 한다.

어떤 궤도는 시간이 무한대로 갈 때, 다른 궤도는 시간이 음의 무한대로 갈 때 극한 주기 궤도에 접근하는 경우, 이를 ''반안정'' 극한 주기 궤도라고 한다.^[14] 안정, 불안정, 반안정 어디에도 속하지 않는 극한 주기 궤도도 존재한다. 예를 들어, 외부 궤도는 극한 주기 궤도에 접근하지만, 내부에서는 다른 주기 궤도들에 의해 접근될 수 있다.

주위 궤도를 끌어당기는 리미트 사이클은 '''점근 안정''' 또는 '''안정'''하다고 하며, 끌개의 한 종류이다. 리야푸노프 지수를 사용하면, 안정 리미트 사이클은 폐궤도 접선 방향의 리야푸노프 지수는 0이고, 그 외 방향은 음의 값을 가진다.^[13]

반대로 주위 궤도를 밀어내는 리미트 사이클은 궤도 불안정 또는 '''불안정'''하다고 한다. 상 평면에서 안쪽 궤도는 흡수되고 바깥쪽 궤도는 반발하거나, 그 반대의 경우, 리미트 사이클은 '''반안정'''하다고 한다.

4. 존재 조건

1차원 자율계의 미분 방정식계에서는 주기해가 존재할 수 없다.^[15] 2차원 자율계 또는 1차원 비자율계 이상에서 주기해가 나타나게 된다.^[16] 극한 주기 궤도는 비선형 계에서만 일어나는 현상으로, 선형계에서는 극한 주기 궤도가 일어나지 않는다.^[17]^[18]

흐름에 따라 상공간의 체적이 변하지 않는 계를 보존계, 체적이 0으로 점근하는 계를 산일계라고 부른다. 산일계에서 극한 주기 궤도가 존재할 가능성이 높다. 주기 궤도가 산일계에 존재하는 경우, 그 주기 궤도의 대부분은 극한 주기 궤도일 것으로 추정된다. 구배계에서도 극한 주기 궤도는 존재하지 않는다.

변수의 시간 미분을 변수 위에 점(·)을 붙여 나타내는 뉴턴의 표기법을 사용하면, 2차원 자율계는 다음과 같이 표현된다.

: $\begin{align}\dot{x} &= f(x,\ y),\\\dot{y} &= g(x,\ y)\end{align}$

이 경우, 닫힌 궤도 및 극한 주기 궤도의 유무를 판별할 수 있는 몇 가지 정리가 있다. 푸앵카레-벤딕손 정리에 따르면, 평형점을 포함하지 않는 유계인 궤도의 극한 집합은 닫힌 궤도이다. 즉, 이러한 궤도는 닫힌 궤도이거나, 존재하는 극한 주기 궤도로 흡인되는 궤도 중 하나이다. 벤딕손의 조건에 의하면, 단일 연결인 영역 위에서

: $\operatorname{div} (f(x,\ y),\ g(x,\ y)) = \frac{\partial f(x,\ y)}{\partial x}+\frac{\partial g(x,\ y)}{\partial y}$

의 값이 0이 아니고, 부호가 일정하다면, 에 완전히 포함된 닫힌 궤도는 존재하지 않는다. 리에나르 방정식에 상당하는 계의 경우, 리에나르의 정리에 의해 원점을 둘러싼 점근 안정인 극한 주기 궤도가 존재한다.

5. 분기

호프 분기는 안정 평형점이 불안정해지면서 안정 극한 주기 궤도가 발생하거나, 불안정 극한 주기 궤도가 불안정 평형점으로 전이하는 현상이다.^[1]

오토 레슬러가 제안한 레스러 방정식은 3차원계에서 극한 주기 궤도가 나타나는 미분 방정식계 중 하나이다. 레슬러 방정식은 다음과 같다.

: $\begin{align}\dot{x} &= -y-z,\\\dot{y} &= x+ay,\\\dot{z} &= b+xz-cz\end{align}$

여기서 $a, b, c$ 는 파라미터이다. 비선형 항은 제3식의 $xz$ 뿐이지만, 레슬러 방정식의 해는 다양한 거동을 보인다.^[16]

예를 들어 $a = 0.1, b = 0.1, c = 4$ 일 때, 레슬러 방정식의 위상 공간에는 안정된 극한 주기 궤도가 나타난다. $a$ 와 $b$ 는 $0.1$ 로 유지하고 $c$ 를 증가시키면, 특정 $c$ 값에서 한 번 감긴 닫힌 곡선이었던 극한 주기 궤도가 두 번 감긴 닫힌 곡선으로 변한다. 즉, 두 바퀴를 돌아야 원래 상태로 돌아오는 닫힌 곡선이 된다.

이처럼 파라미터 $c$ 변화에 따라 주기 $T$ 의 길이가 대략 두 배가 되는 분기를 주기 배가 분기라고 한다. 극한 주기 궤도가 두 번 감기려면 닫힌 궤도가 교차하지 않고 두 바퀴를 돌 수 있는 공간이 필요하다. 따라서 주기 배가 분기는 3차원 이상인 계에서만 일어난다.

주기 배가 분기를 거쳐, $a = 0.1, b = 0.1, c = 6$ 일 때 레슬러 방정식의 극한 주기 궤도는 두 번 감긴(2주기) 상태이다. $c$ 를 더 증가시키면 두 번 감긴 극한 주기 궤도는 네 번 감긴 극한 주기 궤도가 되고, 주기는 다시 두 배가 된다. 이와 같이 $c$ 값 증가에 따라 주기 배가 분기가 계속 일어나, 특정 $c$ 값에서 주기는 무한대가 되고, 극한 주기 궤도는 카오스로 변한다. 이는 계의 끌개가 카오스(스트레인지 어트랙터)로 분기하는 경로 중 하나로, 주기 배가 분기 경로라고 불린다. 예를 들어 $a = 0.1, b = 0.1, c = 9$ 에서 끌개는 카오스이다.

레스러 방정식은 에드워드 로렌츠가 제안한 로렌츠 방정식에서 영감을 받아 도입되었다. 로렌츠 방정식에서도 극한 주기 궤도의 존재와 주기 배가 분기 경로가 확인된다. 또한, 추아 회로에서는 두 개의 극한 주기 궤도가 동시에 존재하고 각각 주기 배가 분기를 하는 모습을 볼 수 있다.

6. 구체적인 예

다음은 극한 주기 궤도의 구체적인 예시이다.

미분 방정식계의 방향장. 원점을 제외한 모든 궤도는 회전하면서 단위 원의 닫힌 궤도에 점근한다.

2차원 미분 방정식계에서,

:

\begin{align}\dot{x} &= x - y - x(x^2 + y^2),\\\dot{y} &= x + y - y(x^2 + y^2)\end{align}

는 극한 주기 궤도를 갖는 예시이다^[15]。 이 계를 극좌표로 나타내면,

:

\begin{align}\dot{r} &= r (1 - r^2),\\\dot{\theta} &= 1\end{align}

이 되어, 동경과 편각의 거동이 서로 무관하게 결정되는 단순한 형태를 가진다. θ의 일반해는 일정 진동수로 계속 회전하는 함수가 된다. r의 일반해는

:

r(t)=\frac{r_0}{\sqrt{r_0^2+(1-r_0^2)e^{-2t}}}

이다. 여기서 r₀는 t = 0에서의 r의 값이다. r₀ ≠ 0이면 r(t)는 t → ∞에서 r → 1이 되어, 계의 원점을 제외한 모든 궤도는 회전하면서 단위 원에 가까워진다^[15]。 따라서 원점을 중심으로 하는 단위원이 이 계의 안정적인 극한 주기 궤도이다.

위의 미분 방정식계에 파라미터 a를 부여한

:

\begin{align}\dot{r} &= r (a - r^2),\\\dot{\theta} &= 1\end{align}

에서는 a > 0이면 반지름 √a의 원이 위와 같이 안정적인 극한 주기 궤도이다. a = 0에서 호프 분기가 일어난다.

발타자르 판 데르 폴이 삼극 진공관의 발진 회로에서 일어나는 자려 진동을 설명하기 위해 유도한 판 데르 폴 방정식은 다음과 같다.

:

\begin{align}\dot{x} &= y,\\\dot{y} &= \mu (1-x^2)y - x\end{align}

여기서 μ > 0는 파라미터이다.

판 데르 폴 방정식의 해는 초등 함수로 나타낼 수 없다. 하지만 원점 주위에 극한 주기 궤도가 존재하고, 초기값이 원점인 경우를 제외하고 모든 궤도가 극한 주기 궤도에 수렴한다. 리에나르의 정리에 의해 판 데르 폴 방정식계의 상 평면에는 유일하고 안정적인 극한 주기 궤도가 존재한다.

판 데르 폴 방정식의 극한 주기 궤도는 μ의 값에 따라 그 형상이 변화한다. μ가 작을수록 극한 주기 궤도는 원 궤도에 가까워진다. μ가 클수록 형상은 원에서 멀어지고, 제1사분면과 제3사분면에서 높이가 높아진다. 이때, 시계열에서는 이완 진동과 같이 완만한 변화와 급격한 변화가 번갈아 나타나는 진동 현상이 일어난다.

3차원계에서 극한 주기 궤도가 나타나는 미분 방정식계로는 레스러 방정식이나 로렌츠 방정식 등이 있다. 오토 레슬러가 제안한 레슬러 방정식은

:

\begin{align}\dot{x} &= -y-z,\\\dot{y} &= x+ay,\\\dot{z} &= b+xz-cz\end{align}

이며, a, b, c는 파라미터이다. 제3식의 xz 항만이 비선형 항임에도 불구하고, 레슬러 방정식의 해는 다양한 거동을 보인다^[16]。

예를 들어 a = 0.1, b = 0.1, c = 4인 경우, 레슬러 방정식의 상공간에는 안정한 극한 주기 궤도가 나타난다. a와 b의 값을 0.1로 유지한 채 c의 값을 늘려가면, 특정 c 값에서 1회 감긴 닫힌 곡선이었던 극한 주기 궤도가 2회 감긴 닫힌 곡선으로 변한다. 즉, 2바퀴 돌아야 원래 상태로 돌아오는 닫힌 곡선이 된다. 파라미터 c의 변화에 따라 주기 T의 길이가 대략 두 배가 되는 분기가 일어나는데, 이를 주기 배가 분기라고 한다. 극한 주기 궤도가 2회 감기려면 닫힌 궤도가 교차하지 않고 2바퀴 돌 수 있는 공간이 필요하다. 따라서 이러한 극한 주기 궤도의 주기 배가 분기는 3차원 이상의 계에서만 일어날 수 있다.

주기 배가 분기를 거쳐, 예를 들어 a = 0.1, b = 0.1, c = 6일 때 레슬러 방정식의 극한 주기 궤도는 2회 감기(2주기) 상태이다. c의 값을 더 늘리면 2회 감기 극한 주기 궤도는 4회 감기 극한 주기 궤도가 되고, 주기는 다시 두 배가 된다. 이와 같이 c 값의 증가에 따라 주기 배가 분기가 계속 일어나, 특정 c 값에서 주기는 무한대가 되고, 극한 주기 궤도에서 카오스로 변한다. 이는 계의 어트랙터가 카오스(스트레인지 어트랙터)로 분기하는 경로 중 하나로, 주기 배가 분기 경로라고 불린다.

레스러 방정식은 에드워드 로렌츠가 제안한 로렌츠 방정식에서 영감을 받아 만들어졌다. 로렌츠 방정식에서도 극한 주기 궤도의 존재와 주기 배가 분기 경로가 확인된다. 추아 회로에서는 2개의 극한 주기 궤도가 동시에 존재하고 각각 주기 배가 분기를 하는 모습을 볼 수 있다.

7. 실제 현상

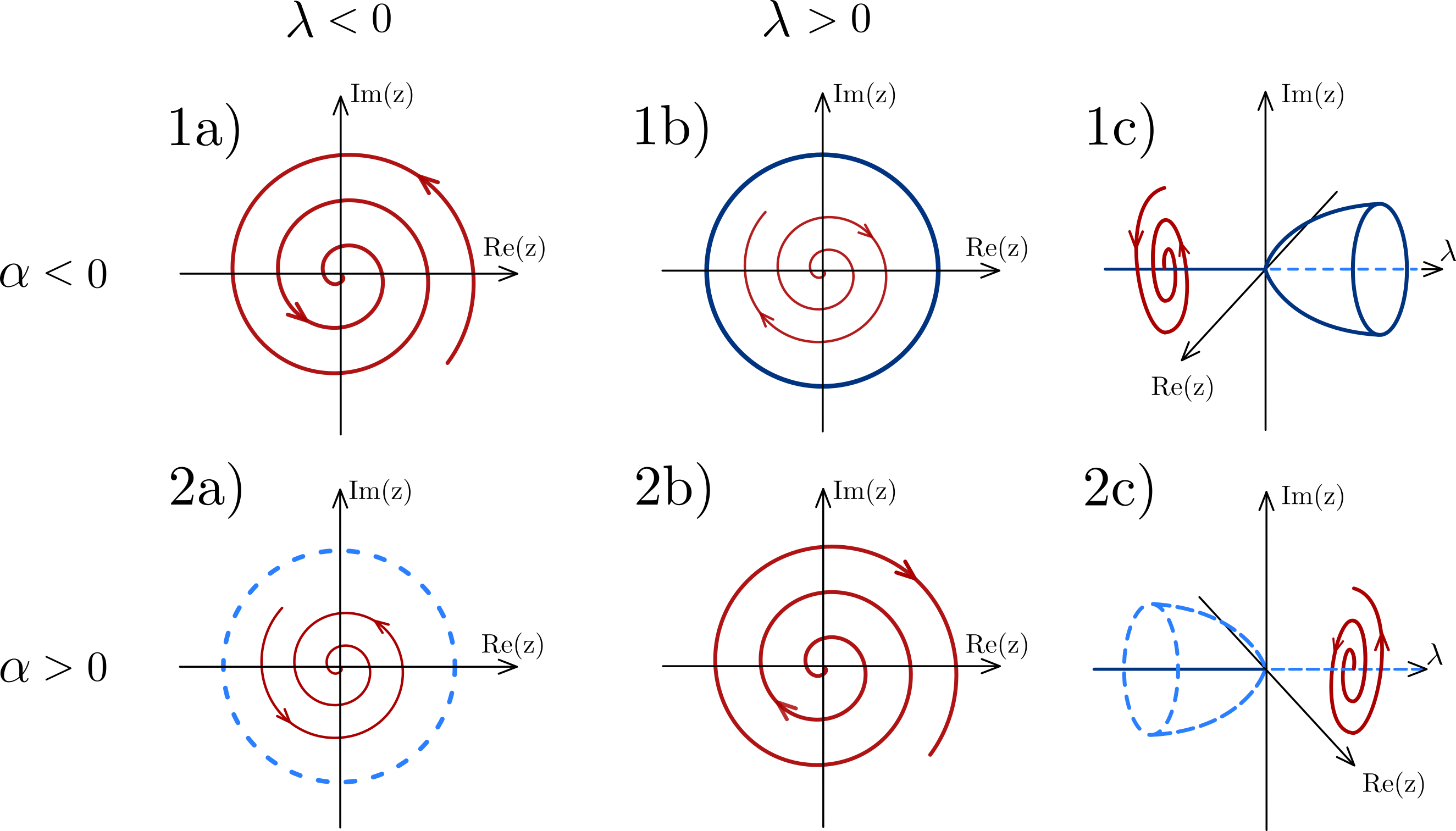
호프 분기 근처의 고정점에서 분기되는 극한 주기 궤도의 예시. 빨간색 궤적, 어두운 파란색의 안정적인 구조, 밝은 파란색의 불안정한 구조. 매개변수 선택은 극한 주기 궤도의 발생과 안정성을 결정한다.

극한 주기 궤도는 자가 진동하는 시스템을 모델링하는 여러 과학 분야에서 중요하게 다루어진다. 주요 예시는 다음과 같다.

공기역학적 극한 주기 진동^[1]
신경 세포의 활동 전위에 대한 호지킨-헉슬리 모델
당분해의 셀코프 모델^[2]
생체 시계의 일부인 동물의 유전자 발현, 호르몬 수치 및 체온의 일일 진동^[3]^[4] (이는 최근 증거와 모순된다.^[5])
제한적인 미세 환경에서 암세포의 세포 이동^[6]
일부 비선형 전기 회로 ( 반 데르 폴 발진기 등)^[7]
매키-글래스 방정식에 나타나는 호흡 및 조혈 작용의 제어^[8]

극한 주기 궤도(리미트 사이클)는 유입되는 에너지는 비진동적임에도 불구하고, 계 자체의 특성으로부터 저절로 발생하는 진동 현상인 자려 진동 현상의 수리 모델이 될 수 있다.^[17] 극한 주기 궤도 진동자는 외력에 의한 강제 진동의 주기에 의존하지 않고 계 자체에서 리듬을 만들어내는 자율성을 지닌다. 또한, 외란이 가해진 경우 일시적으로 진폭이 변화할 수 있지만, 외란이 없어지면 원래의 진폭으로 돌아갈 수 있다. 이러한 극한 주기 궤도의 안정성은 공학 및 생물학적으로 중요하다.^[18]

일정한 리듬을 내는 기계식 메트로놈은 안정적인 리듬의 좋은 예이다. 메트로놈은 처음 바늘을 작게 흔들거나 크게 흔들더라도 일정한 진동으로 안정된다. 메트로놈의 감쇠력과 구동력이 균형을 이루면서 안정적인 진동을 만들어내며, 간단한 모델화를 통해서도 메트로놈에서의 극한 주기 궤도의 존재를 확인할 수 있다. 심장의 박동 등 생물의 리듬 현상 대부분은 항상성을 가지며, 이러한 안정적인 리듬을 기술하는 데 극한 주기 궤도를 갖는 모델이 유효하다.

참조

_[1] 논문 Nonlinear Inviscid Aerodynamic Effects on Transonic Divergence, Flutter, and Limit-Cycle Oscillations https://mems.duke.ed[...] American Institute of Aeronautics and Astronautics 2019-12-09
_[2] 논문 Self-Oscillations in Glycolysis 1. A Simple Kinetic Model 1968
_[3] 논문 Limit Cycle Models for Circadian Rhythms Based on Transcriptional Regulation in Drosophila and Neurospora 1999-12-01
_[4] 논문 Modelling Biological Rhythms 2008-09-09
_[5] 논문 Daily and seasonal adaptation of the circadian clock requires plasticity of the SCN neuronal network. 2010-12
_[6] 논문 Stochastic nonlinear dynamics of confined cell migration in two-state systems 2019
_[7] 논문 Van der Pol and the history of relaxation oscillations: Toward the emergence of a concept 2012-04-30
_[8] 논문 Oscillation and chaos in physiological control systems https://www.science.[...] 1977-07-15
_[9] 논문 Complex dynamics in biological systems arising from multiple limit cycle bifurcation
_[10] 웹사이트 Mathematical Problems - Lecture delivered before the International Congress of Mathematicians at Paris in 1900 - By Professor David Hilbert https://mathcs.clark[...]
_[11] 서적 カオスはこうして発見された共立出版
_[12] 서적 フラクタル科学朝倉書店
_[13] 서적 複雑系入門―知のフロンティアへの冒険 NTT出版
_[14] 서적 振動学コロナ社
_[15] 서적 微分方程式下―その数学と応用丸善出版
_[16] 서적 カオス時系列解析の基礎と応用産業図書
_[17] 서적 機械工学辞典丸善
_[18] 간행물 リミットサイクル，カオスと同期現象入門 http://www.jspf.or.j[...] プラズマ・核融合学会

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com