불연속점의 분류

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 제1종 불연속점
  - 2.1.1. 제거 가능 불연속점
  - 2.1.2. 비약 불연속점
- 2.2. 제2종 불연속점
  - 2.2.1. 무한 불연속점
  - 2.2.2. 진동 불연속점
3. 성질
4. 리만 적분 가능성
5. 도함수의 불연속성
6. 예
7. 한국 사회와 불연속점
참조

1. 개요

불연속점의 분류는 실수 함수의 불연속성을 좌극한과 우극한의 존재 여부에 따라 제1종과 제2종으로 나누는 것이다. 제1종 불연속점은 제거 가능 불연속점과 비약 불연속점으로, 제2종 불연속점은 무한 불연속점과 진동 불연속점으로 세분된다. 불연속점의 성질, 리만 적분 가능성, 도함수의 불연속성 등과 관련된 내용을 다루며, 디리클레 함수, 토메 함수 등을 예시로 든다.

더 읽어볼만한 페이지

해석학 (수학) - 수학적 최적화
수학적 최적화는 주어진 집합에서 실수 또는 정수 변수를 갖는 함수의 최댓값이나 최솟값을 찾는 문제로, 변수 종류, 제약 조건, 목적 함수 개수에 따라 다양한 분야로 나뉘며 여러 학문 분야에서 활용된다.
해석학 (수학) - 라플라스 변환
라플라스 변환은 함수 f(t)를 복소수 s를 사용하여 적분을 통해 다른 함수 F(s)로 변환하는 적분 변환이며, 선형성을 가지고 미분방정식 풀이 등 공학 분야에서 널리 사용된다.

불연속점의 분류

2. 정의

실수 함수의 경우, 불연속점은 좌극한과 우극한의 존재 여부에 따라 '''제1종 불연속점'''과 '''제2종 불연속점'''으로 분류된다. 제1종 불연속점은 좌극한과 우극한이 일치하는지에 따라 '''제거 가능 불연속점'''과 '''비약 불연속점'''으로 분류되며, 제2종 불연속점은 무한대인 좌극한이나 우극한이 있는지에 따라 '''무한 불연속점'''과 '''진동 불연속점'''으로 분류된다.

구체적으로, 정의역이 실수 열린구간 $I\subseteq\mathbb R$ , 공역이 실수 집합 $\mathbb R$ 인 함수 $f\colon I\to\mathbb R$ 가 주어졌다고 하자.

실수 축 위의 점 ''x''₀의 근방에서 정의되는 실수 변수 ''x''의 실수 값을 갖는 함수 ''f''가 점 ''x'' = ''x''₀에서 불연속인 경우를 생각한다.

: $\begin{align}L^{-} &:= \lim_{x\to x_0^{-}} f(x) = f(x_0 - 0), \\L^{+} &:= \lim_{x\to x_0^{+}} f(x) = f(x_0 + 0)\end{align}$

를 각각 ''x'' = ''x''₀에서의 ''f''의 좌극한 또는 우극한으로 한다. 또한, ''L''⁻ = ''L''⁺일 때는 이 일치하는 값을 단순히

: $L := \lim_{x\to x_0^{}} f(x)$

로 나타낸다.

== 제1종 불연속점 ==

제거 가능한 불연속점과 도약 불연속점을 통칭하여 '''제1종 불연속점'''이라고 한다.

=== 제거 가능 불연속점 ===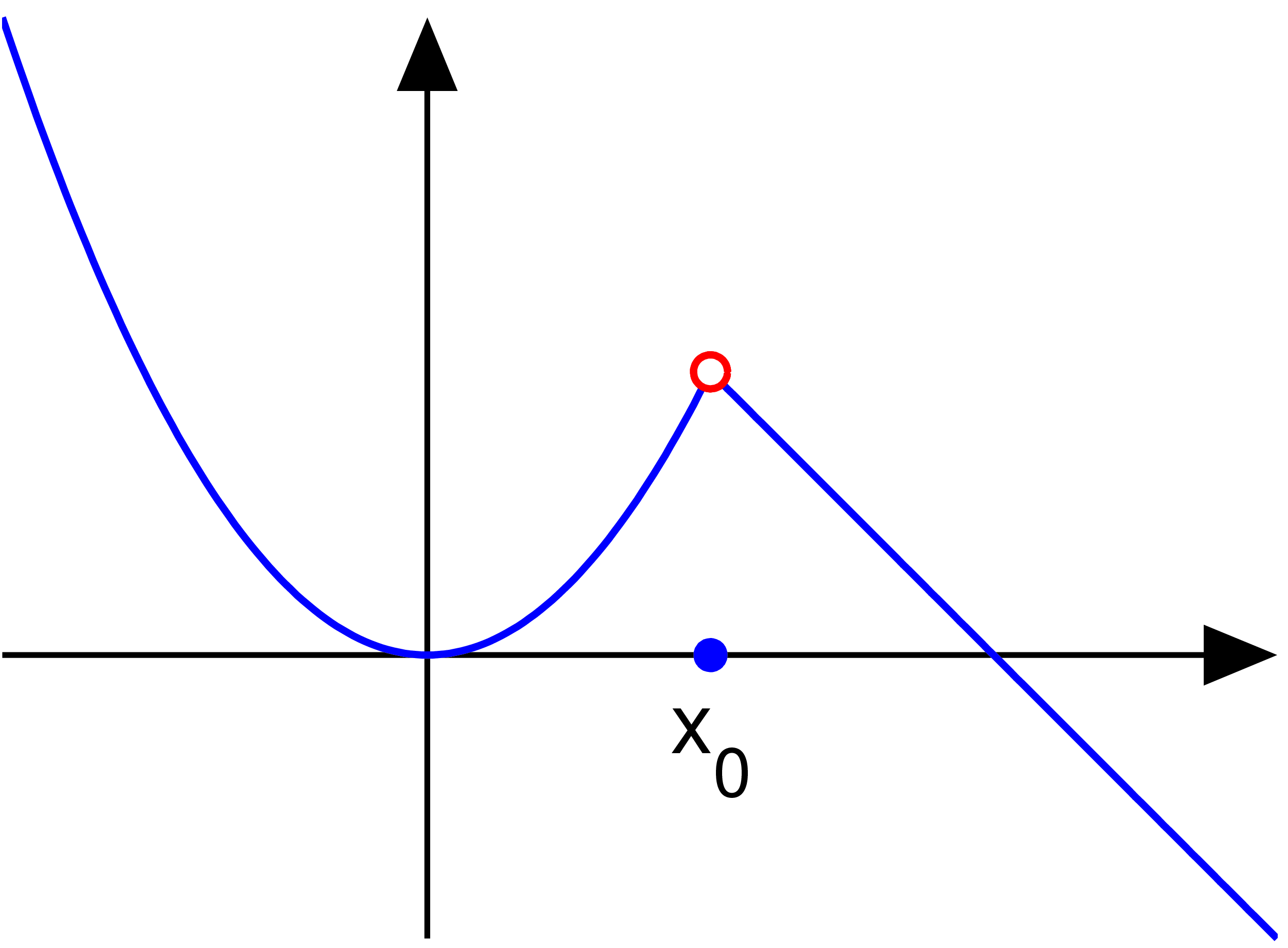

''L''⁻와 ''L''⁺가 유한 확정(존재하고 유한)이고 같지만 ''f''(''x''₀) ≠ ''L''일 때, ''f''(''x'')는 ''x'' = ''x''₀에 '''제거 가능한 불연속점''' removable discontinuity^영어을 갖는다고 한다. ''f''(''x''₀)의 값을 변경하여 "''x'' = ''x''₀에서도 연속이 되도록 할 수 있다"는 의미에서 이 불연속성은 제거할 수 있다. 더 명확히 말하면, 함수

:

g(x) = \begin{cases}f(x) & (x\ne x_0) \\ L & (x = x_0)\end{cases}

는 ''x'' = ''x''₀에서도 연속이 된다.

"제거 가능한 불연속성(점)"이라는 말은, ''x''₀의 좌우 양쪽에서의 극한이 유한 확정이고 같지만, 함수는 ''x''₀에서 정의되지 않는 경우에 잘못 사용되는 경우가 있다.^[13]。그러나 함수의 연속성과 불연속성의 개념은, 함수의 정의역에 속하는 점에 대해서만 정의되므로, 이러한 용법은 부적절하다. 이러한 부정점은 정확히는 제거 가능한 특이점이다.

=== 비약 불연속점 ===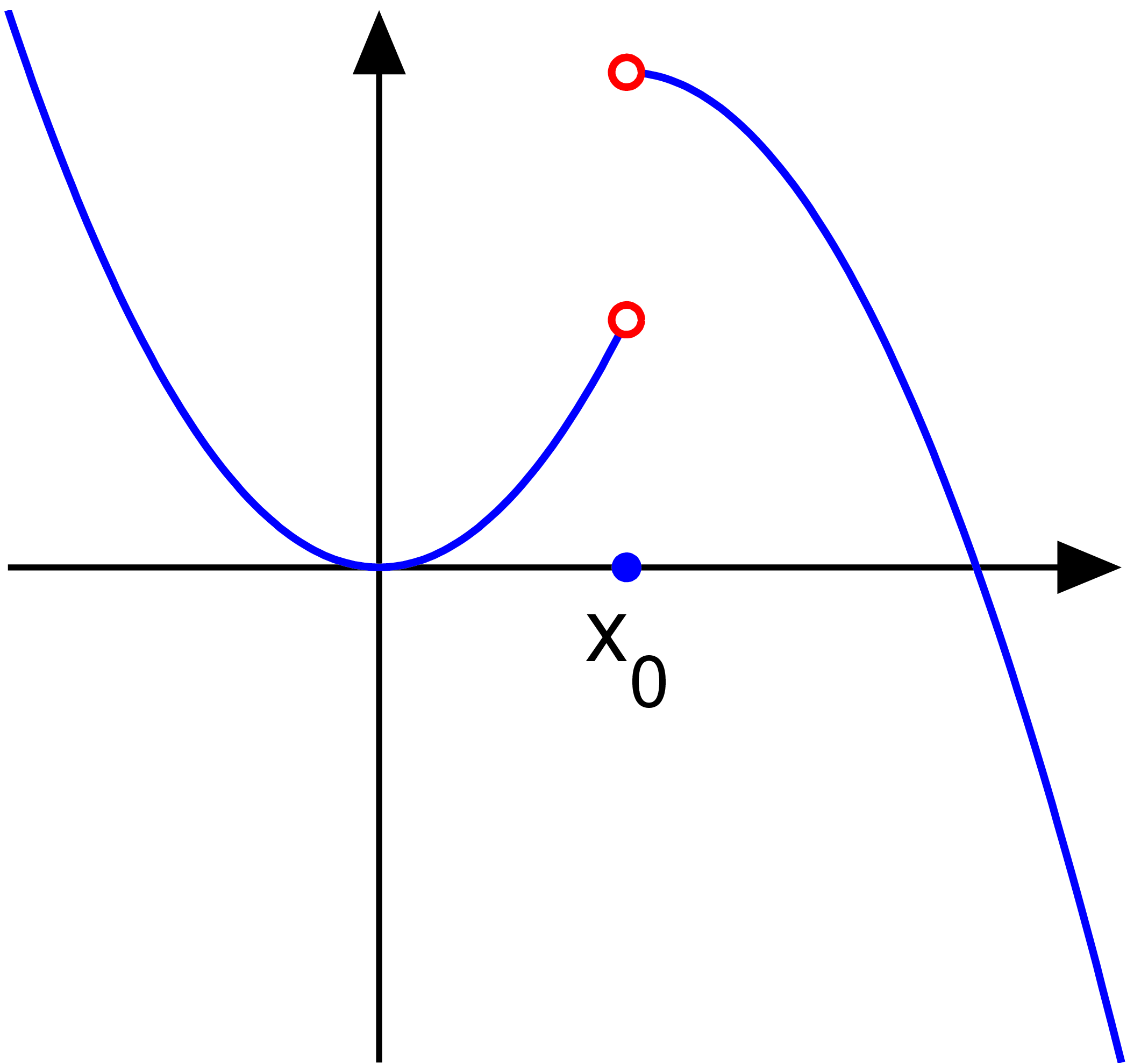

''L''⁻와 ''L''⁺가 유한 확정이나 같지 않은 경우

:

j := L^+ - L^- = f(x_0 + 0) - f(x_0 - 0)

을 함수 ''f''의 ''x''₀에서의 '''도약''', '''점프''' jump^영어, '''계단''' step^영어 또는 '''간극''' gap)^영어 등이라고 하며, ''f''는 ''x'' = ''x''₀에서 도약 ''j''의 '''도약 불연속점''' jump discontinuity^영어, '''계단 불연속점''' step discontinuity^영어 또는 '''간극 불연속점''' gap discontinuity^영어을 갖는다고 한다. 이 불연속성에 대해서는 ''f''(''x''₀)의 값이 무엇인지는 영향을 미치지 않는다(그러나, ''x''₀에서 좌연속 또는 우연속 중 하나로 만들 수 있다).

== 제2종 불연속점 ==

제2종 불연속점은, 한쪽 극한이 존재하지 않는 경우(진성 불연속점)를 말한다.

=== 무한 불연속점 ===

=== 진동 불연속점 ===

2. 1. 제1종 불연속점

불연속점

a\in I

가 다음 조건을 만족시키면, '''제1종 불연속점'''이라고 한다.

(좌·우극한 존재) $\lim_{x\to a^-}f(x)$ 와 $\lim_{x\to a^+}f(x)$ 가 둘 다 존재한다.

편의상,

:

\begin{align}L^{-} &:= \lim_{x\to x_0^{-}} f(x) = f(x_0 - 0), \\L^{+} &:= \lim_{x\to x_0^{+}} f(x) = f(x_0 + 0)\end{align}

를 각각 ''x'' = ''x''₀에서의 ''f''의 좌극한 또는 우극한으로 한다.

제거 가능한 불연속점과 도약 불연속점을 통칭하여 '''제1종 불연속점'''이라고 한다(제거 가능한 불연속점은 도약이 0인 도약 불연속점으로 생각할 수 있다).^[13]

== 제거 가능 불연속점 ==

''L''⁻와 ''L''⁺가 유한 확정(존재하고 유한)이고 같지만 ''f''(''x''₀) ≠ ''L''일 때, ''f''(''x'')는 ''x'' = ''x''₀에 '''제거 가능한 불연속점''' removable discontinuity^영어을 갖는다고 한다. ''f''(''x''₀)의 값을 변경하여 "''x'' = ''x''₀에서도 연속이 되도록 할 수 있다"는 의미에서 이 불연속성은 제거할 수 있다.

== 도약 불연속점 ==

''L''⁻와 ''L''⁺가 유한 확정이나 같지 않은 경우

:

j := L^+ - L^- = f(x_0 + 0) - f(x_0 - 0)

을 함수 ''f''의 ''x''₀에서의 '''도약''', '''점프''' jump^영어, '''계단''' step^영어 또는 '''간극''' gap)^영어 등이라고 하며, ''f''는 ''x'' = ''x''₀에서 도약 ''j''의 '''도약 불연속점''' jump discontinuity^영어, '''계단 불연속점''' step discontinuity^영어 또는 '''간극 불연속점''' gap discontinuity^영어을 갖는다고 한다. 이 불연속성에 대해서는 ''f''(''x''₀)의 값이 무엇인지는 영향을 미치지 않는다(그러나, ''x''₀에서 좌연속 또는 우연속 중 하나로 만들 수 있다).

2. 1. 1. 제거 가능 불연속점

제1종 불연속점

a\in I

가 다음 두 조건 중 적어도 하나를 만족하면

a

를 '''제거 가능 불연속점''' 또는 '''없앨 수 있는 불연속점'''이라고 한다.

(좌·우극한 일치) $\lim_{x\to a^-}f(x)=\lim_{x\to a^+}f(x)$
(극한 존재) $\lim_{x\to a}f(x)$ 가 존재한다.
(제거 가능) $f|_{I\setminus\{a\}}=g|_{I\setminus\{a\}}$ 인 연속 함수 $g\colon I\to\mathbb R$ 가 존재한다.

예를 들어, 1은 다음과 같은 함수의 제거 가능 불연속점이다.

:

f(x)=\begin{cases}x^2&x<1\\0&x=1\\2-x&x>1\end{cases}

제거 가능 불연속점은 함수의 재정의를 통해 연속점으로 만들 수 있다. 예를 들어, 위 함수를 다음과 같이 재정의한다.

:

f(1)=1

그러면, 1은 새로운 함수의 연속점이 된다.

다음과 같은 구간 함수를 고려해 본다.

:

f(x) = \begin{cases}x^2 & \text{ for } x < 1 \\0   & \text{ for } x = 1 \\2-x & \text{ for } x > 1\end{cases}

점

x_0 = 1

은 ''제거 가능한 불연속점''이다.

음의 방향에서 오는 단측 극한:

:

L^- = \lim_{x\to x_0^-} f(x)

양의 방향에서 오는 단측 극한:

:

L^+ = \lim_{x\to x_0^+} f(x)

x_0

에서 ''모두'' 존재하고, 유한하며,

L = L^- = L^+

과 같다. 즉, 두 단측 극한이 존재하고 같으므로,

x

가

x_0

에 접근할 때

f(x)

의 극한

L

이 존재하고 이와 같은 값과 같다. 만약

f\left(x_0\right)

의 실제 값이

L

과 ''같지 않다면'',

x_0

를 '''제거 가능한 불연속점'''이라고 한다. 이 불연속점은

f

가

x_0

에서 연속이 되도록 제거할 수 있다. 더 정확하게는, 함수

:

g(x) = \begin{cases}f(x) & x \neq x_0 \\L & x = x_0\end{cases}

는

x = x_0

에서 연속이다.

''제거 가능한 불연속점''이라는 용어는 때때로 두 방향의 극한이 존재하고 같지만, 함수가 점

x_0

에서 정의되지 않은 제거 가능한 특이점을 포함하도록 확장되기도 한다. 그러나 함수의 연속성과 불연속성은 함수의 정의된 점에 대해서만 정의되는 개념이기 때문에, 이러한 용어의 사용은 부적절하다.

실수 축 위의 점 ''x''₀의 근방에서 정의되는 실수 변수 ''x''의 실수 값을 갖는 함수 ''f''가 점 ''x'' = ''x''₀에서 불연속인 경우를 생각한다.

:

\begin{align}L^{-} &:= \lim_{x\to x_0^{-}} f(x) = f(x_0 - 0), \\L^{+} &:= \lim_{x\to x_0^{+}} f(x) = f(x_0 + 0)\end{align}

를 각각 ''x'' = ''x''₀에서의 ''f''의 좌극한 또는 우극한으로 한다. 또한, ''L''⁻ = ''L''⁺일 때는 이 일치하는 값을 단순히

:

L := \lim_{x\to x_0^{}} f(x)

로 나타낸다.

''L''⁻와 ''L''⁺가 유한 확정(존재하고 유한)이고 같지만 ''f''(''x''₀) ≠ ''L''일 때, ''f''(''x'')는 ''x'' = ''x''₀에 '''제거 가능한 불연속점''' (removable discontinuity)^영어을 갖는다고 한다. ''f''(''x''₀)의 값을 변경하여 "''x'' = ''x''₀에서도 연속이 되도록 할 수 있다"는 의미에서 이 불연속성은 제거할 수 있다. 더 명확히 말하면, 함수

:

g(x) = \begin{cases}f(x) & (x\ne x_0) \\ L & (x = x_0)\end{cases}

는 ''x'' = ''x''₀에서도 연속이 된다.

제거 가능한 불연속점과 도약 불연속점을 통칭하여 '''제1종 불연속점''' (discontinuity of the first kind)^영어이라고 한다(제거 가능한 불연속점은 도약이 0인 도약 불연속점으로 생각할 수 있다).

"제거 가능한 불연속성(점)"이라는 말은, ''x''₀의 좌우 양쪽에서의 극한이 유한 확정이고 같지만, 함수는 ''x''₀에서 정의되지 않는 경우에 잘못 사용되는 경우가 있다.그러나 함수의 연속성과 불연속성의 개념은, 함수의 정의역에 속하는 점에 대해서만 정의되므로, 이러한 용법은 부적절하다. 이러한 부정점은 정확히는 제거 가능한 특이점이다.

2. 1. 2. 비약 불연속점

제1종 불연속점

a\in I

가 다음 두 조건 중 적어도 하나를 만족하면 a를 '''비약 불연속점''' 또는 '''뜀 불연속점'''이라고 한다.

(좌·우극한 불일치) $\lim_{x\to a^-}f(x)\ne\lim_{x\to a^+}f(x)$
(극한 부재) $\lim_{x\to a}f(x)$ 가 존재하지 않는다.

예를 들어, 1은 다음과 같은 함수의 비약 불연속점이다.

:

f(x)=\begin{cases}x^2&x<1\\0&x=1\\2-(x-1)^2&x>1\end{cases}

함수

f(x) = \begin{cases}x^2         & \mbox{ for } x < 1 \\0 \text{ (or possibly undefined)} & \mbox{ for } x = 1 \\2 - (x-1)^2 & \mbox{ for } x > 1\end{cases}

에서, 점

x_0 = 1

은 ''''이다.

이 경우, 좌극한

L^-

과 우극한

L^+

은 존재하고 유한하지만 서로 같지 않기 때문에(

L^- \neq L^+,

), 단일 극한은 존재하지 않는다. 그러면

x_0

을 ''점프 불연속점'', ''계단 불연속점'', 또는 ''제1종 불연속점''이라고 부른다. 이러한 유형의 불연속점의 경우, 함수

f

는

x_0

에서 임의의 값을 가질 수 있다.

실수 축 위의 점 ''x''₀의 근방에서 정의되는 실수 변수 ''x''의 실수 값을 갖는 함수 ''f''가 점 ''x'' = ''x''₀에서 불연속인 경우를 생각할때,

:

\begin{align}L^{-} &:= \lim_{x\to x_0^{-}} f(x) = f(x_0 - 0), \\L^{+} &:= \lim_{x\to x_0^{+}} f(x) = f(x_0 + 0)\end{align}

를 각각 ''x'' = ''x''₀에서의 ''f''의 좌극한 또는 우극한으로 한다. ''L''⁻ = ''L''⁺일 때는 이 일치하는 값을 단순히

:

L := \lim_{x\to x_0^{}} f(x)

로 나타낸다.

''L''⁻와 ''L''⁺가 유한 확정이나 같지 않은 경우

:

j := L^+ - L^- = f(x_0 + 0) - f(x_0 - 0)

을 함수 ''f''의 ''x''₀에서의 '''도약''', '''점프''' (jump)^영어, '''계단''' (step)^영어 또는 '''간극''' (gap)^영어 등이라고 하며, ''f''는 ''x'' = ''x''₀에서 도약 ''j''의 '''도약 불연속점''' (jump discontinuity)^영어, '''계단 불연속점''' (step discontinuity)^영어 또는 '''간극 불연속점''' (gap discontinuity)^영어을 갖는다고 한다. 이 불연속성에 대해서는 ''f''(''x''₀)의 값이 무엇인지는 영향을 미치지 않는다(그러나, ''x''₀에서 좌연속 또는 우연속 중 하나로 만들 수 있다).

2. 2. 제2종 불연속점

불연속점

a\in I

가 다음 조건을 만족시키면, '''제2종 불연속점'''이라고 한다.

(좌/우극한 부재) $\lim_{x\to a^-}f(x)$ 와 $\lim_{x\to a^+}f(x)$ 가운데 적어도 하나가 존재하지 않는다.

실수 축 위의 점 ''x''₀의 근방에서 정의되는 실수 변수 ''x''의 실수 값을 갖는 함수 ''f''가 점 ''x'' = ''x''₀에서 불연속인 경우를 생각한다. 편의상,

:

\begin{align}L^{-} &:= \lim_{x\to x_0^{-}} f(x) = f(x_0 - 0), \\L^{+} &:= \lim_{x\to x_0^{+}} f(x) = f(x_0 + 0)\end{align}

를 각각 ''x'' = ''x''₀에서의 ''f''의 좌극한 또는 우극한으로 한다.

제2종 불연속점은, 한쪽 극한이 존재하지 않는 경우(진성 불연속점)를 말한다.

2. 2. 1. 무한 불연속점

제2종 불연속점

a\in I

가 다음 조건을 만족시키면, '''무한 불연속점'''이라고 한다.

(좌/우극한 무한대) $\lim_{x\to a^-}f(x)$ 와 $\lim_{x\to a^+}f(x)$ 가운데 적어도 하나가 사영 무한대 $\hat\infty$ 이다.

예를 들어, 1은 다음과 같은 함수의 무한 불연속점이다.

:

f(x)=\begin{cases}\sin\frac5{x-1}&x<1\\0&x=1\\\frac1{x-1}&x>1\end{cases}

2. 2. 2. 진동 불연속점

a\in I

가 다음 조건을 만족시키면, '''진동 불연속점'''이라고 한다.

(좌·우극한 무한대 아님) $\lim_{x\to a^-}f(x)$ 가 사영 무한대 $\hat\infty$ 가 아니며, $\lim_{x\to a^+}f(x)$ 가 사영 무한대 $\hat\infty$ 가 아니다.

예를 들어, 1은 다음과 같은 함수의 진동 불연속점이다.

:

f(x)=\begin{cases}\sin\frac5{x-1}&x\ne1\\0&x=1\end{cases}

필수 불연속점의 경우, 적어도 한쪽의 극한은

\mathbb{R}

에서 존재하지 않는다. (한쪽 또는 양쪽 극한이

\pm\infty

일 수도 있다.)

다음 함수를 생각해 보자.

f(x) = \begin{cases}\sin\frac{5}{x-1} & \text{ for } x < 1 \\0                 & \text{ for } x = 1 \\\frac{1}{x-1}     & \text{ for } x > 1.\end{cases}

이때, 점

x_0 = 1

은 ''''이다.

이 예시에서,

L^-

과

L^+

둘 다

\mathbb{R}

에서 존재하지 않으므로 필수 불연속점의 조건을 만족한다. 따라서

x_0

는 필수 불연속점, 무한 불연속점, 또는 제2종 불연속점이다. (이것은 복소 변수 함수의 연구에서 종종 사용되는 본질적 특이점과는 다르다.)

제2종 불연속점은, 한쪽 극한이 존재하지 않는 경우(진성 불연속점)를 말한다.

3. 성질

함수의 연속점 집합은 항상 G_δ 집합이다.^[2] 함수의 불연속점 집합은 항상 F_σ 집합이다.^[2]

실변수 실숫값 함수의 제1종 불연속점 집합은 가산 집합이다. 특히, 실변수 실숫값 단조함수의 불연속점은 항상 제1종 불연속점이므로, 단조함수의 불연속점 집합은 커야 가산 집합이다. 이를 '''프로다의 정리'''(Froda's theorem^영어)라고 한다.^[3]^[4]^[5]

함수 *f*가 구간 *I* ⊆ R에서 정의되었다고 가정하면, *D*를 *I*에서 *f*의 모든 불연속점의 집합으로 나타낸다. *R*은 *f*가 *x*₀에서 ''제거 가능한'' 불연속성을 갖는 모든 *x*₀∈ *I*의 집합을 의미한다. 유사하게 *J*는 *f*가 *x*₀에서 ''점프'' 불연속성을 갖는 모든 *x*₀∈ *I*로 구성된 집합을 나타낸다. *f*가 *x*₀에서 ''본질적인'' 불연속성을 갖는 모든 *x*₀∈ *I*의 집합은 *E*로 나타낸다.

집합 *D*는 $F_{\sigma}$ 집합이다.
구간 *I*에서, *f*가 단조 함수이면, *D*는 최대 가산이며, *D* = *J*이다. 이것은 프로다 정리이다.

토메 함수는 모든 유리수 점에서 불연속이지만, 모든 무리수 점에서 연속이다. 디리클레 함수로 알려진, 유리수 전체의 집합의 지시 함수는 모든 곳에서 불연속이다.

4. 리만 적분 가능성

르베그의 정리(르베그-비탈리 정리)에 따르면, 유계 함수 f가 I = [a,b]에서 리만 적분 가능할 필요충분조건은 불연속점 집합의 르베그 측도가 0인 것이다.^[10]

이는 모든 종류의 불연속성이 유계 함수 f가 [a,b]에서 리만 적분 가능하지 않게 만드는 데 동일한 비중을 갖는 것처럼 보이지만, 가산 집합은 르베그 측도 0인 집합이고, 르베그 측도 0인 집합들의 가산 합집합 역시 르베그 측도 0인 집합이므로, 그렇지 않다. 집합 R ∪ J ∪ E₂ ∪ E₃의 불연속성은 f의 리만 적분 가능성과 관련하여 중립적이다. 주요 불연속성은 제1종 본질적 불연속성이다.^[10]

따라서 르베그-비탈리 정리는 다음과 같이 다시 쓸 수 있다.

유계 함수 f가 [a,b]에서 리만 적분 가능할 필요충분조건은 f의 모든 제1종 본질적 불연속성의 해당 집합 E₁이 르베그 측도 0을 갖는 것이다.^[10]

만약 E₁ = ∅ 이라면, 이는 유계 함수 f : [a, b] → ℝ의 리만 적분 가능성에 대한 고전적인 보완적인 상황에 해당한다.^[10]

f가 [a, b]의 각 점에서 우극한을 갖는다면, f는 [a, b]에서 리만 적분 가능하다.^[10]
f가 [a, b]의 각 점에서 좌극한을 갖는다면, f는 [a, b]에서 리만 적분 가능하다.^[10]
f가 [a, b]에서 조절 함수라면, f는 [a, b]에서 리만 적분 가능하다.^[10]

5. 도함수의 불연속성

다르부 정리에 따르면, 도함수는 중간값 성질을 만족한다. 즉, 연속 함수가 아니더라도 중간값을 취한다.^[11] 도함수의 불연속점은 제거 가능 불연속점이나 점프 불연속점이 될 수 없고, 본질적 불연속점만이 가능하다.^[11] 특히, 극한값이 무한대가 되는 불연속점은 도함수의 불연속점이 될 수 없다.^[12]

6. 예

디리클레 함수는 모든 점에서 불연속이며, 이 불연속점은 모두 진동 불연속점이다. 토메 함수는 모든 유리수 점에서 불연속이며, 이 불연속점은 모두 제거 가능 불연속점이다.

전체 유리수를 나열한 수열 $(r_n)_{n=0}^\infty$ 에 대하여, 함수 $f(x)=\sum_{n\in\mathbb N\colon r_n 를 정의하면, f 는 유리수 집합에서 불연속인 증가함수가 되며, 이들 불연속점은 모두 제거 가능 불연속점이다.$

함수

: $f(x)=\begin{cases}x^2 & \mbox{ for } x< 1 \\ 0 & \mbox { for } x=1 \\ 2-x& \mbox{ for } x>1\end{cases}$

에서 ''x''₀ = 1은 제거 가능한 불연속점이다. ''f''(''x'')의 ''x'' = 1에서의 값을 1로 변경하면 연속이 된다.

함수

: $f(x)=\begin{cases}x^2 & \mbox{ for } x< 1 \\ 0 & \mbox { for } x=1 \\ 2-(x-1)^2& \mbox{ for } x>1\end{cases}$

에서 ''x''₀ = 1은 점프 불연속점이다.

함수

: $f(x)=\begin{cases}\sin\frac{5}{x-1} & \mbox{ for } x< 1 \\ 0 & \mbox { for } x=1 \\ \frac{0.1}{x-1}& \mbox{ for } x>1\end{cases}$

에서 ''x''₀ = 1은 본질적 불연속점이다. 극한의 어느 한쪽이 존재하지 않거나 무한대이면 본질적 불연속점이 된다. 이 함수를 복소수 변수로 확장해도 불연속성은 본질적이다.

칸토어 집합의 지시 함수 $\mathbf 1_\mathcal{C}(x)$ 는 칸토어 집합의 모든 점에서 제1종 본질적 불연속성을 가지는 리만 적분 가능한 함수이다.

7. 한국 사회와 불연속점

참조

_[1] 웹사이트 Mathwords: Removable Discontinuity http://www.mathwords[...]
_[2] 서적 An Introduction to Classical Real Analysis American Mathematical Society
_[3] 서적 Mathematical Analysis Addison and Wesley
_[4] 서적 Principles of Mathematical Analysis McGraw-Hill
_[5] 서적 Op. cit.
_[6] 서적 Op. cit.
_[7] 서적 Op. cit.
_[8] 서적 The Century Dictionary: An Encyclopedic Lexicon of the English Language https://books.google[...] T. Fisher Unwin and The Century Company
_[9] 간행물 Advanced Advanced Calculus: Counting the Discontinuities of a Real-Valued Function with Interval Domain http://about.jstor.o[...] 1989-02
_[10] 간행물 On Riemann Integrability https://doi.org/10.1[...] 1971
_[11] 서적 Op.cit.
_[12] 간행물 On a discontinuity of a derivative http://dx.doi.org/10[...] 2000
_[13] 웹사이트 Mathwords での定義の最後の一文 http://www.mathwords[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com