십사각형

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정십사각형
- 2.1. 성질
- 2.2. 작도
3. 대칭
4. 분할
5. 관련 도형
- 5.1. 페트리 다각형
참조

1. 개요

십사각형은 모든 변의 길이와 각의 크기가 같은 정다각형으로, 슐래플리 기호 {14}로 나타낸다. 한 변의 길이가 a인 정십사각형의 면적은 약 15.3345a²이며, 중심각과 외각은 25.714°이고, 내각은 154.285°이다. 정십사각형은 자와 컴퍼스만으로는 작도할 수 없지만, 뉴시스 작도 또는 눈금 있는 자를 사용하면 작도가 가능하다. 십사각형은 Dih₁₄ 대칭을 가지며, 말레이시아 국기에도 14개 점의 별의 형태로 나타난다.

더 읽어볼만한 페이지

변의 수에 따른 다각형 - 오각형
다섯 변으로 이루어진 다각형인 오각형은 변의 길이와 각의 크기가 모두 같은 정오각형을 포함하며, 정오각형은 컴퍼스와 자로 작도할 수 있고 자연에서도 발견된다.
변의 수에 따른 다각형 - 육각형
육각형은 여섯 변과 꼭짓점으로 이루어진 다각형으로, 특히 모든 변과 각이 같은 정육각형은 평면 테셀레이션이 가능하고 벌집 구조, 건축, 자연 현상, 한국 전통 문양 등 다양한 분야에서 활용된다.

십사각형
다각형 정보
종류	다각형
변의 수	14
꼭짓점 수	14
면의 수	1
일반적인 특징 (정십사각형)
슈 퇫칭글리 기호	{14}
대칭군	이면군 (Dih14)
넓이 (변의 길이 t)	수식: A = (14/4)t^2 cot(π/14) ≈ 15.3345 t^2
내각	수식: 180(14-2)/14 = 154.2857143 도

2. 정십사각형

정십사각형은 모든 변의 길이와 각의 크기가 같은 십사각형이다. 한 변의 길이가 ''a''인 정십사각형의 면적 S는 다음과 같이 나타낼 수 있다.

: $S = \frac{14}{4}a^2\cot\frac{\pi}{14}\simeq 15.3345a^2$

$\sin\frac{2\pi}{14}$ 와 $\cos\frac{2\pi}{14}$ 를 제곱근과 세제곱근으로 나타내면 다음과 같다.

: $\sin\frac{2\pi}{14} = \frac{\sqrt{3\left(28-2\sqrt[3]{28-84i\sqrt{3}}-2\sqrt[3]{28+84i\sqrt{3}}\right)}}{12}$

: $\cos\frac{2\pi}{14} = \frac{\sqrt{3\left(20+2\sqrt[3]{28-84i\sqrt{3}}+2\sqrt[3]{28+84i\sqrt{3}}\right)}}{12}$

2. 1. 성질

정십사각형은 슐래플리 기호 {14}를 가지며, 두 종류의 변을 교대로 가지는 준정 절단된 칠각형, t{7}으로 구성될 수 있다.

한 변의 길이가 ''a''인 정십사각형의 면적은 다음과 같다.

:

정십사각형에서 중심각과 외각은 25.714…°이며, 내각은 154.285…°이다.

를 제곱근과 세제곱근으로 나타내면 다음과 같다.

:} + \sqrt{7} \cdot \sqrt[3]{\frac{-1-3\sqrt{3} \cdot i}{2\sqrt{7}}} + 1 \right)

2. 2. 작도

14 = 2 × 7이므로 정십사각형은 자와 컴퍼스만으로는 작도할 수 없다.^[1] 그러나 뉴시스 작도를 사용하거나, 각의 삼등분선을 이용하거나,^[2] 눈금 있는 자를 사용하면 작도가 가능하다.^[3]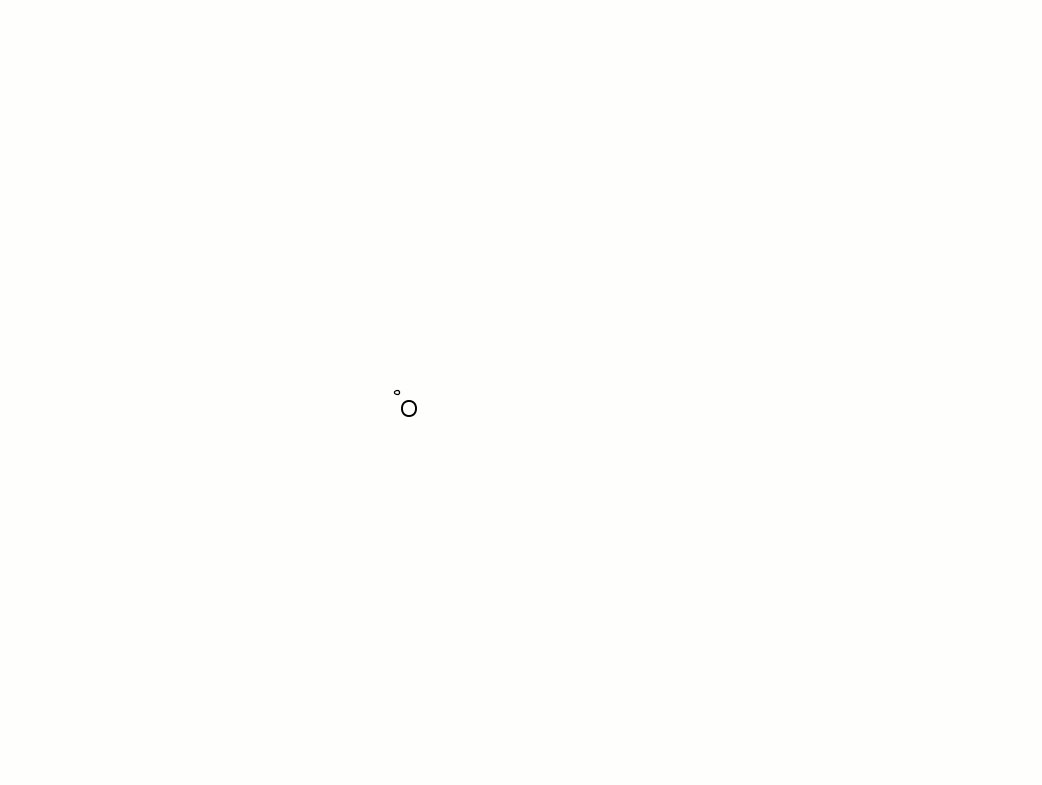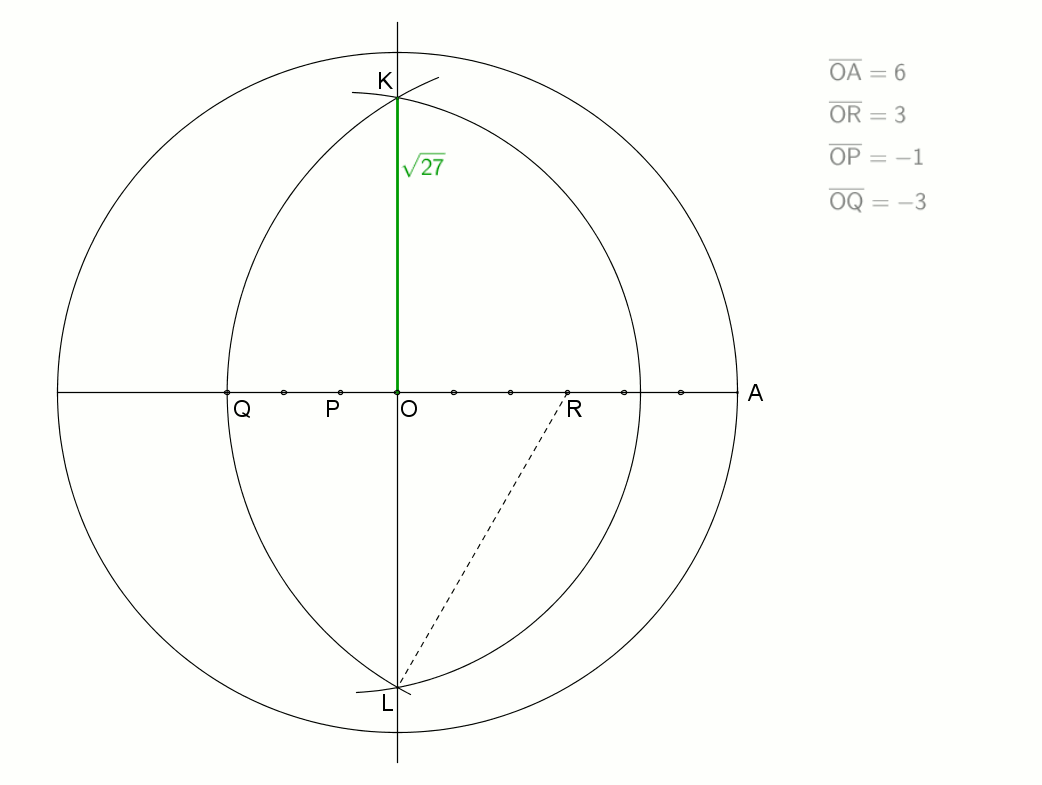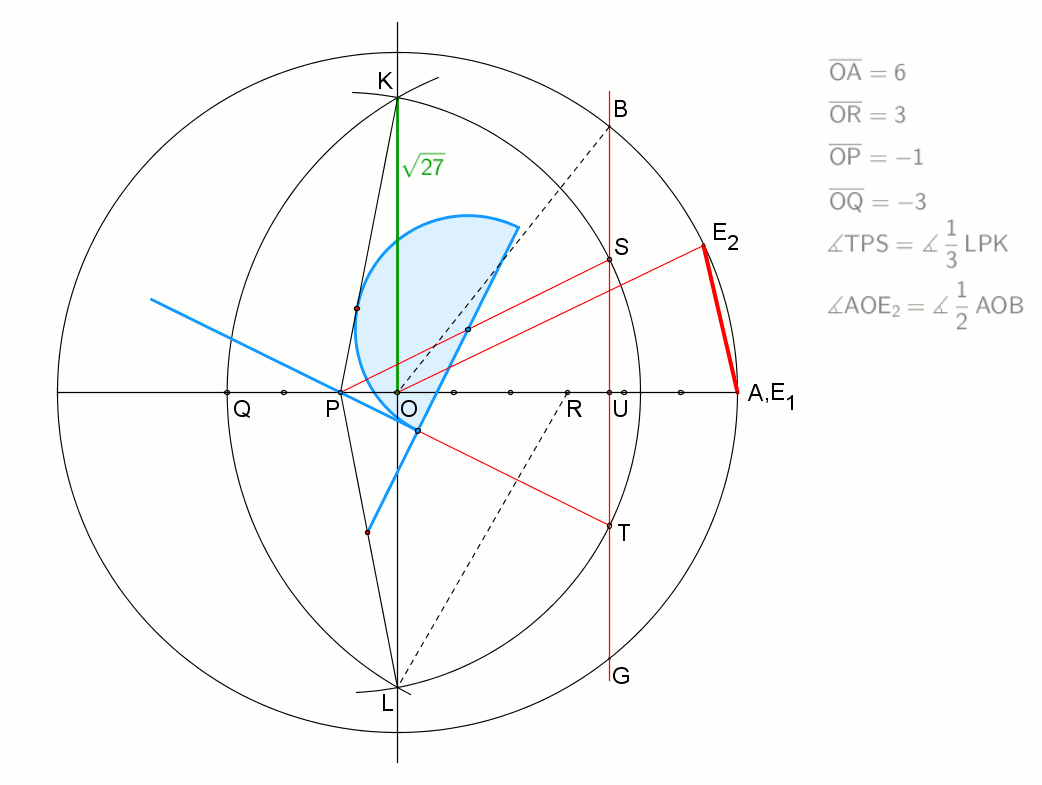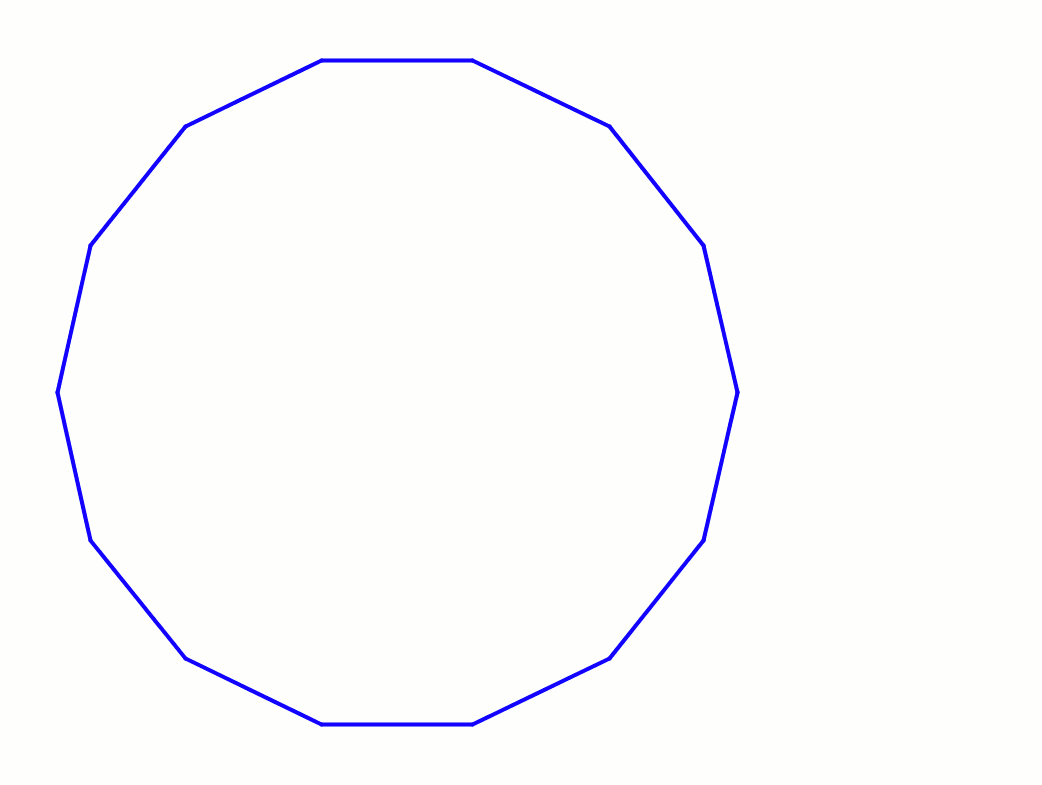

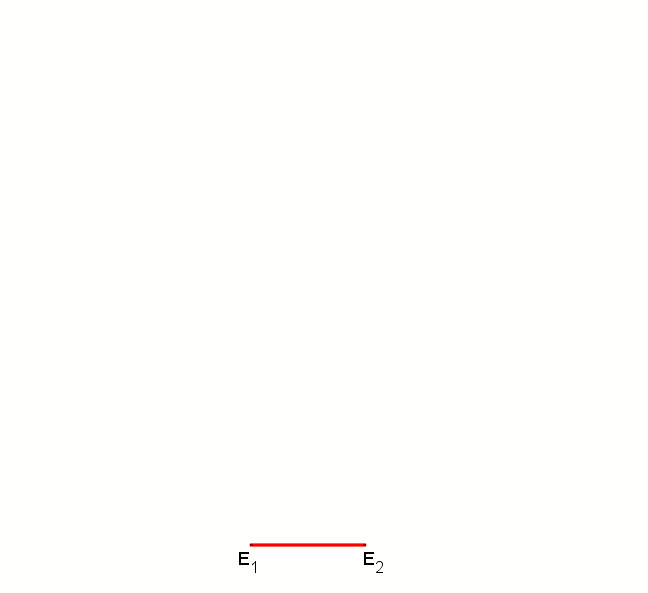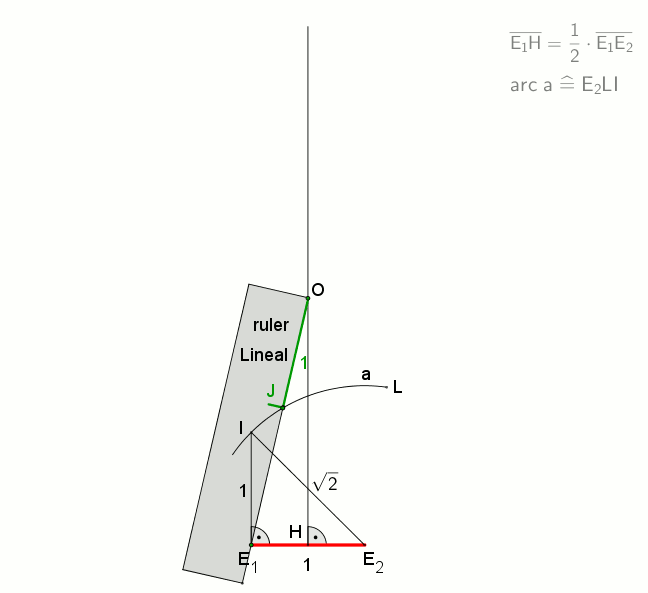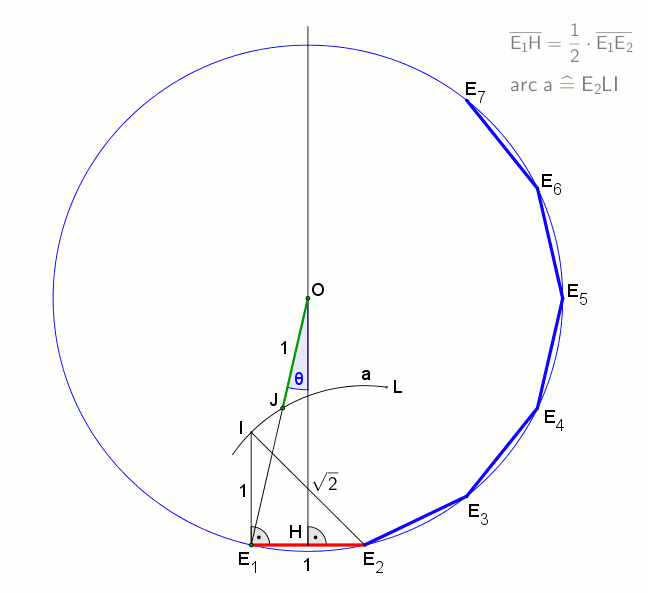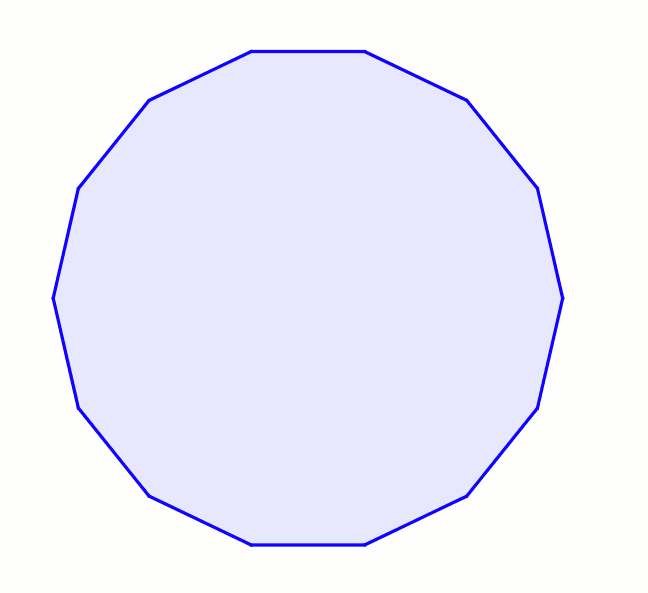
주어진 변의 길이를 가진 십사각형: 데이비드 존슨 리스크(크로켓 존슨)에 따른 눈금 있는 자를 이용한 뉴시스 작도의 애니메이션(1분 20초).

3. 대칭

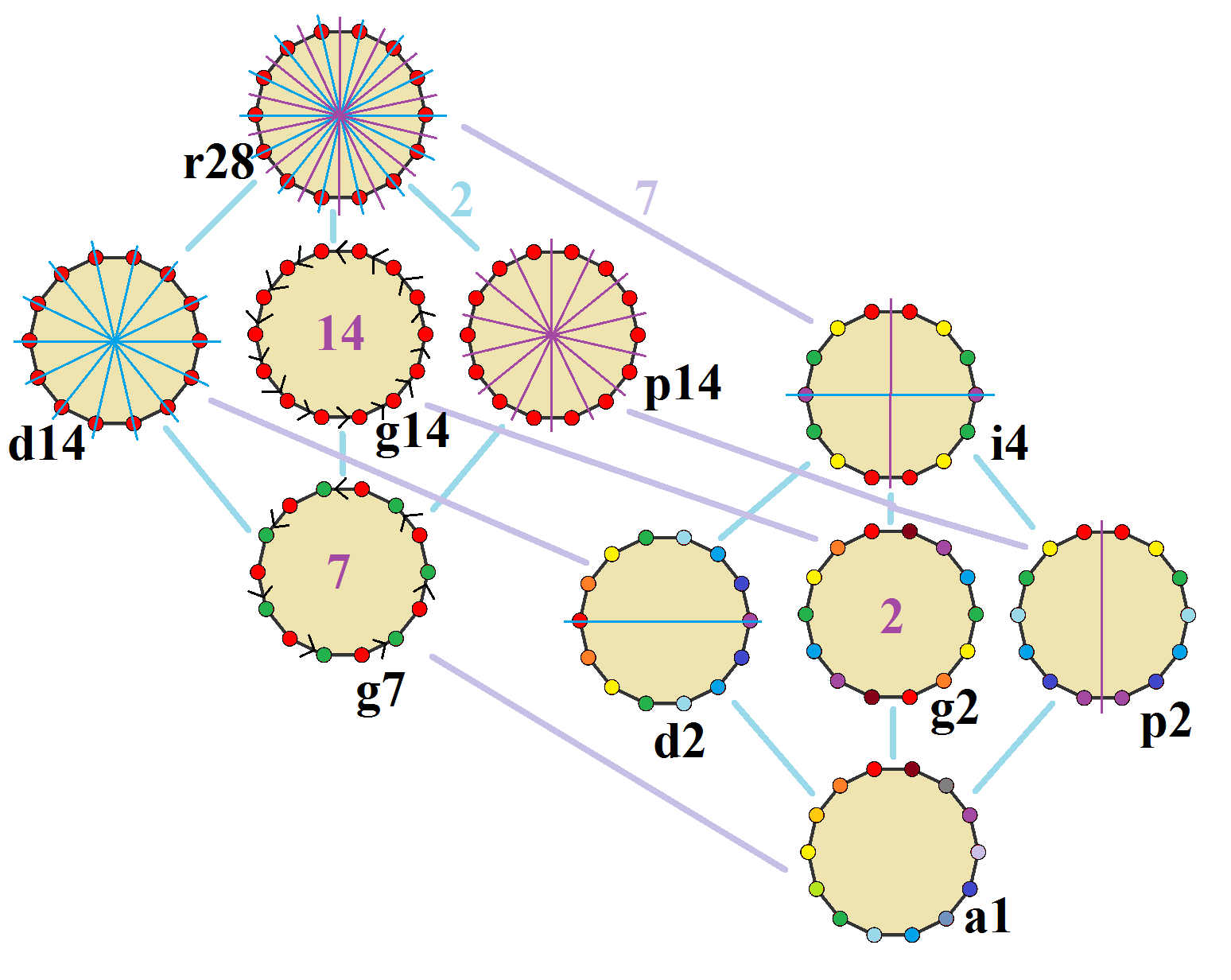
정십사각형의 대칭. 꼭짓점은 대칭 위치별로 색상이 지정되어 있다. 파란색 거울은 꼭짓점을 통과하여 그려지고, 보라색 거울은 모서리를 통과하여 그려진다. 회전 차수는 중앙에 주어집니다.

정십사각형은 Dih₁₄ 대칭을 가지며, 차수는 28이다. Dih₇, Dih₂, Dih₁의 3개의 부분군 이면각 대칭과 Z₁₄, Z₇, Z₂, Z₁의 4개의 순환군 대칭이 있다.

존 콘웨이는 십사각형의 대칭을 문자와 군의 차수로 표시하는데,^[4] 정규 형태의 전체 대칭은 '''r28'''이며, '''a1'''로 표시된 대칭은 없다. 이면각 대칭은 꼭짓점을 통과하는지(대각선 '''d''') 또는 모서리를 통과하는지(수직 '''p''')에 따라 구분되며, 반사선이 모서리와 꼭짓점 모두를 통과하는 경우 '''i'''로 표시한다. 중간 열의 순환 대칭은 중심 회전 차수에 대해 '''g'''로 표시된다.

각 부분군 대칭은 불규칙한 형태에 대해 하나 이상의 자유도를 허용한다. '''g14''' 부분군만이 자유도가 없지만 유향 모서리로 볼 수 있다.

가장 높은 대칭의 불규칙 십사각형은 긴 모서리와 짧은 모서리가 교대로 나타날 수 있는 7개의 거울로 구성된 등각 십사각형인 '''d14'''와 동일한 모서리 길이로 구성되지만 꼭짓점이 두 개의 다른 내각을 교대로 나타나는 등각 십각형인 '''p14'''이다. 이 두 형태는 서로의 쌍대 다각형이며 정십사각형의 절반의 대칭 차수를 가진다.

4. 분할

코세터는 모든 존오곤(마주보는 변이 평행하고 길이가 같은 2''m''각형)은 ''m''(''m''-1)/2개의 평행사변형으로 분할될 수 있다고 설명한다.^[5] 특히 이것은 짝수 개의 변을 가진 정다각형에 해당하며, 이 경우 평행사변형은 모두 마름모이다. 정십사각형의 경우, ''m''=7이고, 21개(7개의 마름모 3세트)로 나눌 수 있다. 이 분해는 7-정육면체의 페트리 다각형 투영을 기반으로 한다.

21개의 마름모로 분할

5. 관련 도형

'''십각형별'''은 14개의 면을 가진 별 모양 다각형으로, 기호 {14/n}으로 표시된다. 정규 별 다각형으로는 {14/3}과 {14/5}가 있다. 이들은 같은 꼭짓점을 사용하지만, 각각 세 번째, 다섯 번째 점마다 연결하여 만들어진다.^[7]

십사각형별은 세 개의 화합물 형태로도 나타낼 수 있다. {14/2}는 두 개의 칠각형 (2{7})으로, {14/4}와 {14/6}은 각각 두 개의 칠각별 (2{7/2}, 2{7/3})로, {14/7}은 7개의 이각형으로 축소된다.

말레이시아 국기에는 14개의 점을 가진 별이 있는데, 이는 말레이시아의 13개 주와 연방 정부의 단결을 상징한다.^[6]

n	1	2	3	4	5	6	7
형식	정규	화합물	별 다각형	화합물	별 다각형	화합물
그림	{14/1} = {14}	{14/2} = 2{7}	{14/3}	{14/4} = 2{7/2}	{14/5}	{14/6} = 2{7/3}	{14/7} 또는 7{2}
내각	≈154.286°	≈128.571°	≈102.857°	≈77.1429°	≈51.4286°	≈25.7143°	0°

5. 1. 페트리 다각형

정규 비틀린 십사각형은 여러 고차원 Petrie 다각형으로 존재하며, 다음의 비틀린 직교 투영에서 볼 수 있다.

B₇	2I₂(7) (4D)	A₁₃	D₈	E₈
7-정축체	7-입방체	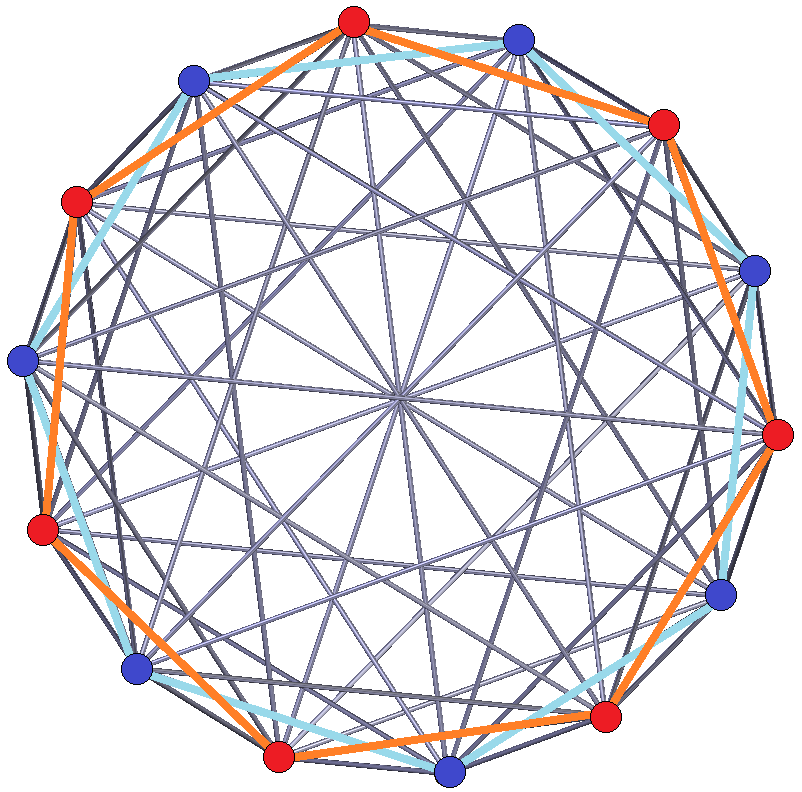7-7 이중각뿔	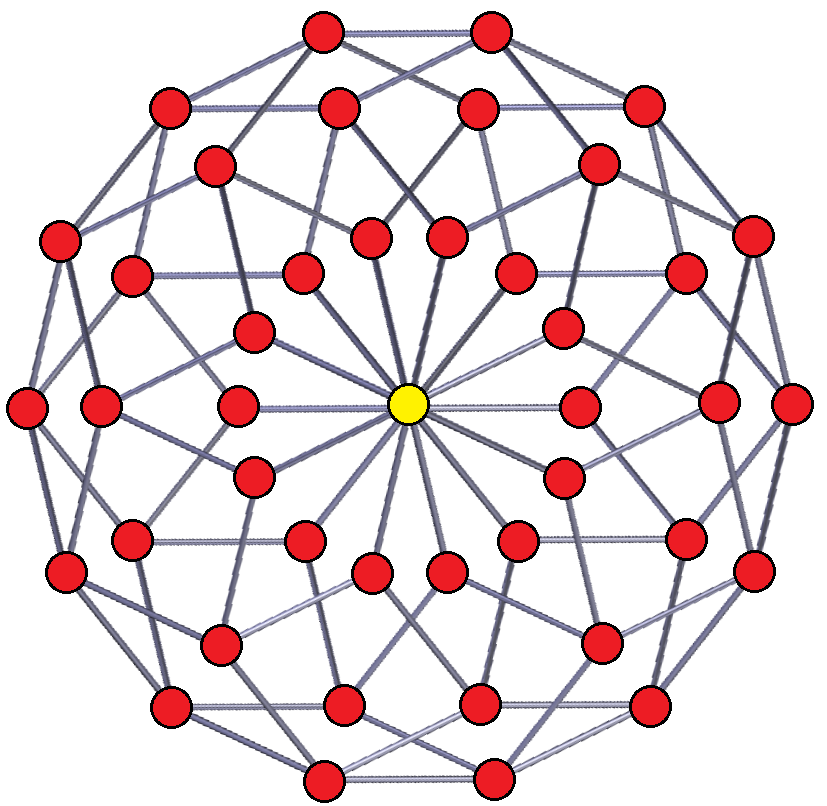7-7 이중기둥	13-단순체	5₁₁	1₅₁	4₂₁	2₄₁

참조

_[1] 학술지 Recherches sur les moyens de Reconnaître si un Problème de géométrie peau se résoudre avec la règle et le compas http://sites.mathdoc[...] 1837
_[2] 학술지 Angle trisection, the heptagon, p. 186 (Fig.1) –187 http://apollonius.ma[...] 1988-03
_[3] 웹사이트 Heptagon http://mathworld.wol[...]
_[4] 서적 The Symmetries of Things 2008
_[5] 서적 Mathematical recreations and Essays
_[6] 간행물 The Numismatist American Numismatic Association 1983
_[7] 간행물 Metamorphoses of polygons 1994

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com