칠각형

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정칠각형의 성질
- 2.1. 면적
- 2.2. 대각선
3. 작도
4. 대칭성
5. 별 모양 칠각형 (칠각별)
6. 타일링과 채움
7. 현실에서의 예
참조

1. 개요

칠각형은 모든 변과 각의 크기가 같은 정다각형으로, 한 내각의 크기는 약 128.57도이다. 정칠각형은 14개의 대각선을 가지며, 대각선의 길이는 두 종류로 나뉜다. 정칠각형의 면적은 한 변의 길이를 이용하여 계산할 수 있으며, 외접원 또는 내접원을 통해서도 면적을 구할 수 있다.

정칠각형은 자와 컴퍼스만으로는 작도가 불가능하며, 특수한 도구나 뉴시스 작도를 사용하거나, 근사적인 작도 방법을 통해 그릴 수 있다. 정칠각형은 칠각별을 만들 수 있으며, 타일링과 채움에도 활용된다. 현실에서는 동전, 건축물, 배지, 우표 등 다양한 형태로 사용된다.

더 읽어볼만한 페이지

7 - 천칭궁
천칭궁은 9월 23일부터 10월 23일(혹은 24일) 사이의 별자리로 저울로 상징되며 공정성, 균형, 조화를 나타내고 쌍둥이자리, 물병자리와 함께 공기 별자리에 속하며 금성이 다스리는 별자리로 여겨진다.
7 - 아메샤 스펜타
아메샤 스펜타는 조로아스터교에서 아후라 마즈다로부터 발현된 일곱 신적 존재를 지칭하며, 창조의 도구로서 특정 창조물과 연결되어 조로아스터교 우주론의 중요한 부분을 차지하고 인간이 추구해야 할 도덕적 자질을 상징한다.
변의 수에 따른 다각형 - 오각형
다섯 변으로 이루어진 다각형인 오각형은 변의 길이와 각의 크기가 모두 같은 정오각형을 포함하며, 정오각형은 컴퍼스와 자로 작도할 수 있고 자연에서도 발견된다.
변의 수에 따른 다각형 - 육각형
육각형은 여섯 변과 꼭짓점으로 이루어진 다각형으로, 특히 모든 변과 각이 같은 정육각형은 평면 테셀레이션이 가능하고 벌집 구조, 건축, 자연 현상, 한국 전통 문양 등 다양한 분야에서 활용된다.

칠각형
개요
칠각형
종류	다각형
변의 수	7
꼭짓점 수	7
슈플리 기호	{7}
속성	볼록
정칠각형
내부각	128.5714286도
특징	작도 불가능

2. 정칠각형의 성질

'''정정다각형'''인 칠각형은 모든 변과 모든 각이 같으며, 내각은 5π/7^la 라디안(128 도)이다. 슐레플리 기호는 {7}이다.

'''정칠각형'''(正七角形, regular heptagon^영어)은 각 변의 길이가 같고, 모든 내각의 크기도 같은 칠각형을 가리킨다. 하나의 내각은 5π/7^la라디안(128과 4/7도)이며, 하나의 외각과 중심각은 모두 2π/7^la라디안(51과 3/7도)이다. 한 변의 길이를 ''a''라고 하면 둘레는 7''a''이다.

정칠각형에는 모두 14개의 대각선을 그릴 수 있는데, 대각선의 길이는 2종류밖에 없다. 즉, 두 개의 이웃한 꼭짓점을 연결하는 짧은 대각선 ''b''와, 세 개의 이웃한 꼭짓점을 연결하는 긴 대각선 ''c''이다.

중심에서 꼭짓점까지의 거리는 외접원의 반지름 ''R''과 같고

:

R = \frac{1}{2} a \frac{1}{\sin \frac{\pi}{7}}

이다. 중심에서 변까지의 최단 거리는 내접원의 반지름 ''r''과 같고

:

r = \frac{1}{2} a \cot \frac{\pi}{7}

이다.

위의 세 길이는

:

a = 2R \sin \frac{\pi}{7},~ b = 2R \sin \frac{2\pi}{7},~ c = 2R \sin \frac{3\pi}{7}

로 나타낼 수 있다. 이들 사이에는 다음과 같은 관계식이 알려져 있다.

:

\frac{1}{a} = \frac{1}{b} + \frac{1}{c}

정칠각형에 얽힌 여러 값은 구하기 어려운 경우가 많다. 예를 들어, 정칠각형의 작도를 논할 때 중요한

\cos \frac{2\pi}{7} \approx 0.62349

는 삼차 방정식

8x^3+4x^2-4x-1=0

의 해 중 하나이다. 마찬가지로, 정칠각형에 얽힌 각도의 삼각함수의 값은 그 유리수 체상 최소 다항식이 삼차식이나 육차식이 된다.^[11]

== 면적 ==

한 변의 길이가 ''a''인 정칠각형의 면적(''A'')은 다음과 같이 주어진다.

:

A = \frac{7}{4}a^2 \cot \frac{\pi}{7} \simeq 3.634 a^2.

이는 정칠각형을 7개의 삼각형으로 나누고, 각 삼각형을 아포템을 이용하여 다시 반으로 나누어 유도할 수 있다. 아포템은

\pi/7

의 코탄젠트의 절반이며, 14개의 작은 삼각형 각각의 면적은 아포템의 4분의 1이다.

반지름 ''R''인 원에 내접하는 정칠각형의 면적은

\tfrac{7R^2}{2}\sin\tfrac{2\pi}{7}

이며, 이는 외접원 면적

\pi R^2

의 약 0.8710에 해당한다.

== 대각선 ==

정칠각형의 변 *a*, 짧은 대각선 *b*, 긴 대각선 *c*는 *a* < *b* < *c*를 만족하며, 다음 관계를 갖는다.^[7]

:

a^2=c(c-b),

:

b^2 =a(c+a),

:

c^2 =b(a+b),

:

\frac{1}{a}=\frac{1}{b}+\frac{1}{c}

(광학 방정식)

:

ab+ac=bc,

:

b^3+2b^2c-bc^2-c^3=0,

:

c^3-2c^2a-ca^2+a^3=0,

:

a^3-2a^2b-ab^2+b^3=0,

^[7]

–*b*/ *c*, *c*/ *a*, *a*/ *b*는 모두 삼차 방정식

t^3-2t^2-t + 1=0

을 만족한다. 하지만 이 방정식의 해는 환원 불가능 경우에 해당하여, 순수한 실수 항을 가진 대수식으로 표현할 수 없다.

정칠각형의 변을 기준으로 한 대각선의 근사 길이는 다음과 같다.^[8]

:

b\approx 1.80193\cdot a, \qquad c\approx 2.24698\cdot a.

또한 다음을 만족한다.

:

b^2-a^2=ac,

:

c^2-b^2=ab,

:

a^2-c^2=-bc,

:

\frac{b^2}{a^2}+\frac{c^2}{b^2}+\frac{a^2}{c^2}=5.

정칠각형에는 모두 14개의 대각선을 그릴 수 있으며, 대각선의 길이는 짧은 대각선 ''b''와 긴 대각선 ''c'' 두 종류이다.

2. 1. 면적

한 변의 길이가 ''a''인 정칠각형의 면적(''A'')은 다음과 같이 주어진다.

:

A = \frac{7}{4}a^2 \cot \frac{\pi}{7} \simeq 3.634 a^2.

이는 정칠각형을 7개의 삼각형으로 나누고, 각 삼각형을 아포템을 이용하여 다시 반으로 나누어 유도할 수 있다. 아포템은

\pi/7

의 코탄젠트의 절반이며, 14개의 작은 삼각형 각각의 면적은 아포템의 4분의 1이다.

반지름 ''R''인 원에 내접하는 정칠각형의 면적은

\tfrac{7R^2}{2}\sin\tfrac{2\pi}{7}

이며, 이는 외접원 면적

\pi R^2

의 약 0.8710에 해당한다. 중심에서 꼭짓점까지의 거리는 외접원의 반지름 ''R''과 같고, :

R = \frac{1}{2} a \frac{1}{\sin \frac{\pi}{7}}

이다. 중심에서 변까지의 최단 거리는 내접원의 반지름 ''r''과 같고, :

r = \frac{1}{2} a \cot \frac{\pi}{7}

이다.

2. 2. 대각선

정칠각형의 변 *a*, 짧은 대각선 *b*, 긴 대각선 *c*는 *a* < *b* < *c*를 만족하며, 다음 관계를 갖는다.^[7]

:

a^2=c(c-b),

:

b^2 =a(c+a),

:

c^2 =b(a+b),

:

\frac{1}{a}=\frac{1}{b}+\frac{1}{c}

(광학 방정식)

:

ab+ac=bc,

:

b^3+2b^2c-bc^2-c^3=0,

:

c^3-2c^2a-ca^2+a^3=0,

:

a^3-2a^2b-ab^2+b^3=0,

^[7]

–*b*/ *c*, *c*/ *a*, *a*/ *b*는 모두 삼차 방정식

t^3-2t^2-t + 1=0

을 만족한다. 하지만 이 방정식의 해는 환원 불가능 경우에 해당하여, 순수한 실수 항을 가진 대수식으로 표현할 수 없다.

정칠각형의 변을 기준으로 한 대각선의 근사 길이는 다음과 같다.^[8]

:

b\approx 1.80193\cdot a, \qquad c\approx 2.24698\cdot a.

또한 다음을 만족한다.

:

b^2-a^2=ac,

:

c^2-b^2=ab,

:

a^2-c^2=-bc,

:

\frac{b^2}{a^2}+\frac{c^2}{b^2}+\frac{a^2}{c^2}=5.

칠각형 삼각형은 정칠각형의 첫 번째, 두 번째, 네 번째 꼭짓점을 꼭짓점으로 가지며, 각도는

\pi/7, 2\pi/7,

4\pi/7

이다.^[7]

정칠각형에는 모두 14개의 대각선을 그릴 수 있으며, 대각선의 길이는 짧은 대각선 ''b''와 긴 대각선 ''c'' 두 종류이다.

3. 작도

정7각형은 자와 컴퍼스만으로는 작도 가능한 다각형을 작도할 수 없다. 7은 페르마 소수가 아니기 때문이다. 이러한 성질을 가진 가장 작은 정다각형이다. 자와 컴퍼스만으로 작도가 불가능하다는 것은 $\scriptstyle {2\cos{\tfrac{2\pi}{7}} \approx 1.247}$ 이 기약 다항식 3차 함수 ''x''³ + ''x''² − 2''x'' − 1의 근이라는 것에서 비롯된다. 이 다항식은 2cos(2π/7)의 최소 다항식인데, 작도 가능한 수의 최소 다항식의 차수는 2의 거듭제곱이어야 하기 때문이다.

정칠각형을 컴퍼스와 자만으로는 작도하는 것이 불가능하다는 것이 증명되었다.^[12] 현대에는, 이것은 길이가 $\cos \frac{2\pi}{7}$ 인 선분을 작도할 수 없는 것에 귀착하여 설명되는 경우가 많다.

== 뉴시스 작도 ==

7은 페르마 소수는 아니지만 피어폰트 소수이므로, 정칠각형은 일반적으로 작도가 불가능하지만 눈금이 있는 자를 이용한 뉴시스(Neusis) 작도로는 작도가 가능하다.^[13]

== 기타 작도 방법 ==

정칠각형은 페르마 소수는 아니지만 피어폰트 소수이므로, 일반적인 컴퍼스와 자 (길이 측정이 불가능한 것)만으로는 작도가 불가능하다.^[12] 하지만, 다른 도구를 사용하면 작도가 가능하다.

예를 들어, 7이 피어폰트 소수이므로, 눈금자(길이 측정이 가능한 것)를 사용하거나, 각의 삼등분을 할 수 있는 도구, 또는 종이접기 공리에 따른 종이접기를 이용하면 정칠각형을 작도할 수 있다.^[13]

고대에는 아르키메데스가 원뿔 곡선의 교차를 사용하여 정칠각형을 작도했다는 기록이 있지만, 이 책은 현재 전해지지 않는다. 사비트 이븐 쿠라 등의 이슬람 수학자들이 아르키메데스의 책을 언급하며 정칠각형을 작도했다고 한다.^[13]

컴퍼스와 자 외에 임의의 각을 삼등분할 수 있는 도구(각의 삼등분기, angle trisector)를 사용하면, 다음 식을 근거로 정칠각형을 작도할 수 있다.

: $\cos \frac{2\pi}{7} = \frac{1}{6} \left( 2\sqrt{7} \cdot \cos \left( \frac{ \arctan{3 \sqrt3} }{3} \right) - 1 \right)$

:즉, 가로세로비가 3√3:1인 직각삼각형의 예각 중 하나를 삼등분하는 조작을 거치면 된다.

종이접기 공리에 따라 종이접기를 하면, 이미 작도된 수를 계수로 하는 임의의 삼차 방정식을 풀 수 있으므로, $8x^3+4x^2-4x-1=0$ 의 해를 작도하여 정칠각형을 작도할 수 있다.

눈금자와 컴퍼스를 사용하여 뉴시스(Neusis) 작도 (눈금자를 종이 위에서 미끄러뜨리면서 위치를 찾는 작도)를 하는 경우에도 정칠각형을 작도할 수 있다.

그 외에도, 히피아스의 원적곡선을 이용하거나 각의 칠등분기를 제작하여 정칠각형을 정확하게 작도할 수 있다.

== 근사적 작도 ==

알렉산드리아의 헤론이나 알브레히트 뒤러의 저서에서 칠각형의 한 변의 길이를 근사하는 방법이 제시되었는데, 오차는 약 0.2%이다.^[2]^[3] 이 방법은 동일한 원에 내접하는 정삼각형의 한 변의 절반 길이를 칠각형의 한 변의 길이로 사용하는 것이다.

단위 원에 내접하는 칠각형의 변의 길이는 $\scriptstyle 2\sin{\pi \over 7} \approx 0.86777$ 인데, 이 근사법에서는 $\scriptstyle {\sqrt{3} \over 2} \approx 0.86603$ 을 사용한다.

외접원의 반지름이 1m일 때, 이 근사법으로 인한 변의 길이 오차는 약 -1.7mm이다.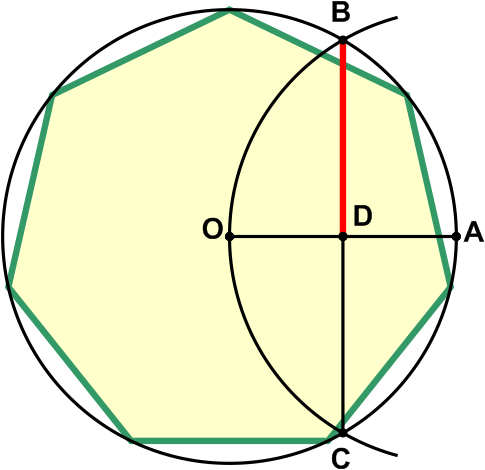

3. 1. 뉴시스 작도

7은 페르마 소수는 아니지만 피어폰트 소수이므로, 정칠각형은 일반적으로 작도가 불가능하지만 눈금이 있는 자를 이용한 뉴시스(Neusis) 작도로는 작도가 가능하다.^[13] 뉴시스 작도를 통해 정칠각형을 작도할 수 있다.^[13]

3. 2. 기타 작도 방법

정칠각형은 페르마 소수는 아니지만 피어폰트 소수이므로, 일반적인 컴퍼스와 자 (길이 측정이 불가능한 것)만으로는 작도가 불가능하다.^[12] 하지만, 다른 도구를 사용하면 작도가 가능하다.

예를 들어, 7이 피어폰트 소수이므로, 눈금자(길이 측정이 가능한 것)를 사용하거나, 각의 삼등분을 할 수 있는 도구, 또는 종이접기 공리에 따른 종이접기를 이용하면 정칠각형을 작도할 수 있다.^[13]

고대에는 아르키메데스가 원뿔 곡선의 교차를 사용하여 정칠각형을 작도했다는 기록이 있지만, 이 책은 현재 전해지지 않는다. 사비트 이븐 쿠라 등의 이슬람 수학자들이 아르키메데스의 책을 언급하며 정칠각형을 작도했다고 한다.^[13]

컴퍼스와 자 외에 임의의 각을 삼등분할 수 있는 도구(각의 삼등분기, angle trisector)를 사용하면, 다음 식을 근거로 정칠각형을 작도할 수 있다.

:

\cos \frac{2\pi}{7} = \frac{1}{6} \left( 2\sqrt{7} \cdot \cos \left( \frac{ \arctan{3 \sqrt3} }{3} \right) - 1 \right)

:즉, 가로세로비가 3√3:1인 직각삼각형의 예각 중 하나를 삼등분하는 조작을 거치면 된다.

종이접기 공리에 따라 종이접기를 하면, 이미 작도된 수를 계수로 하는 임의의 삼차 방정식을 풀 수 있으므로,

8x^3+4x^2-4x-1=0

의 해를 작도하여 정칠각형을 작도할 수 있다.

눈금자와 컴퍼스를 사용하여 뉴시스(Neusis) 작도 (눈금자를 종이 위에서 미끄러뜨리면서 위치를 찾는 작도)를 하는 경우에도 정칠각형을 작도할 수 있다.

그 외에도, 을 이용하거나 각의 칠등분기를 제작하여 정칠각형을 정확하게 작도할 수 있다.

3. 3. 근사적 작도

알렉산드리아의 헤론이나 알브레히트 뒤러의 저서에서 칠각형의 한 변의 길이를 근사하는 방법이 제시되었는데, 오차는 약 0.2%이다.^[2]^[3] 이 방법은 동일한 원에 내접하는 정삼각형의 한 변의 절반 길이를 칠각형의 한 변의 길이로 사용하는 것이다.

단위 원에 내접하는 칠각형의 변의 길이는

\scriptstyle 2\sin{\pi \over 7} \approx 0.86777

인데, 이 근사법에서는

\scriptstyle {\sqrt{3} \over 2} \approx 0.86603

을 사용한다.

외접원의 반지름이 1m일 때, 이 근사법으로 인한 변의 길이 오차는 약 -1.7mm이다.

4. 대칭성

정칠각형은 D_7h 점군(쇼엔플리스 표기법)에 속하며 차수는 28이다.^[5] 대칭 요소는 7중 회전축 C₇, 7중 부적절 회전축 S₇, 7개의 수직 거울 평면 σ_v, 7개의 2중 회전축 C₂ (칠각형 평면에 위치), 그리고 칠각형 평면에 위치한 수평 거울 평면 σ_h이다.^[6]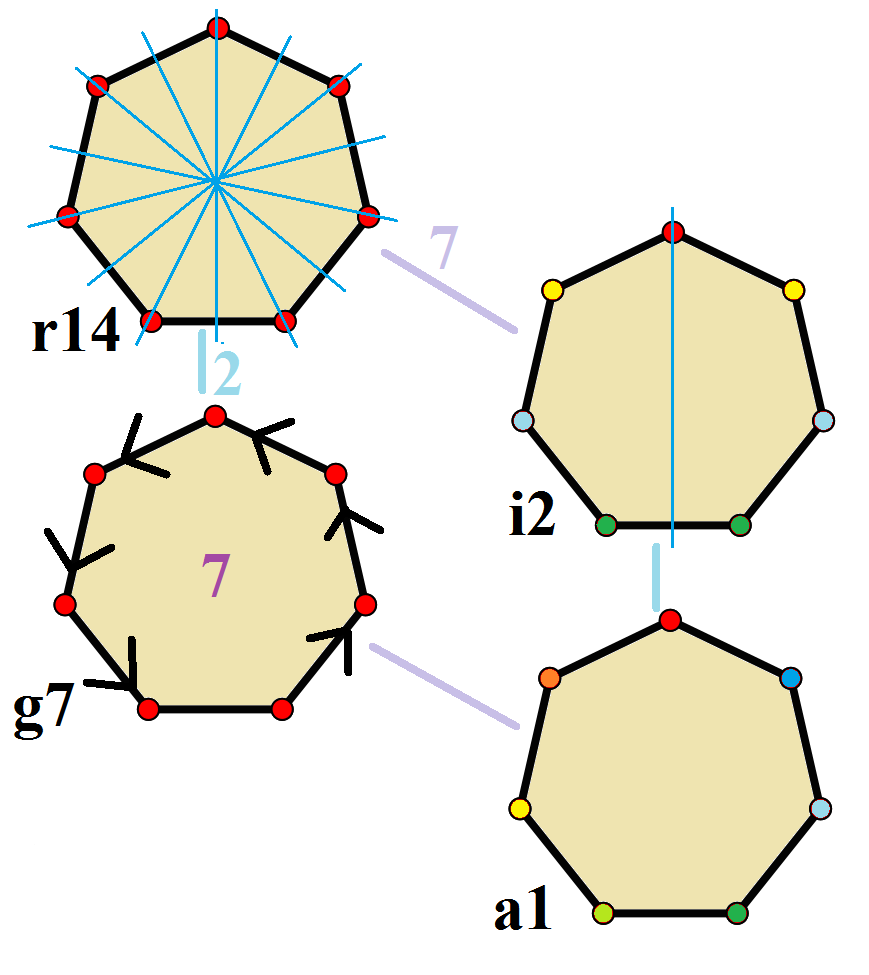

5. 별 모양 칠각형 (칠각별)

정칠각형에서 두 종류의 칠각별을 만들 수 있으며, 슐래플리 기호 {7/2}와 {7/3}으로 표시하고, 약수는 연결 간격을 나타낸다.

6. 타일링과 채움

정삼각형, 칠각형, 42각형은 평면의 정점을 완전히 채울 수 있다. 그러나 이 다각형만으로는 평면 타일링을 할 수 없는데, 그 이유는 틈을 만들거나 겹치지 않고 삼각형의 세 번째 변에 이들 중 하나를 맞출 방법이 없기 때문이다.^[9] 쌍곡 평면에서는 정칠각형으로 타일링하는 것이 가능하다.^[9] 유클리드 평면에서도 오목 칠각형 타일링이 가능하다.^[9]

정칠각형으로 유클리드 평면을 가장 조밀하게 채운 이중 격자 채움, 모든 볼록 집합 중 가장 낮은 최대 채움 밀도를 가질 것으로 추정됨

정칠각형은 약 0.89269의 채움 밀도를 갖는 유클리드 평면의 이중 격자 채움을 갖는다. 이는 모든 볼록 집합의 최적 이중 격자 채움 밀도, 더 일반적으로 모든 볼록 집합의 최적 채움 밀도에 대해 가능한 가장 낮은 밀도로 추정된다.^[10]

7. 현실에서의 예

영국은 1982년 이후 50펜스와 20펜스 두 종류의 칠각형 동전을 사용하고 있으며, 바베이도스 달러 또한 칠각형이다. 이 동전들은 엄밀히 말하면 뢸로 칠각형으로, 자동판매기에 넣을 때 부드럽게 굴러가도록 가장자리가 굽어 있다. 보츠와나 풀라 동전 중 일부(2 풀라, 1 풀라, 50 테베, 5 테베)도 뢸로 칠각형 모양이며, 이 외에도 모리셔스, 아랍에미리트, 탄자니아 등 여러 나라에서 뢸로 칠각형 동전이 통용된다. 잠비아의 1000 콰차 동전은 진정한 칠각형이다.

브라질의 25센트 동전에는 칠각형이 새겨져 있으며, 조지아 국장의 일부 옛 버전은 칠각별을 요소로 사용했다.

20유로 센트 동전을 포함한 일부 동전은 스페인 꽃이라고 하는 칠각형 대칭 모양을 갖는다.

건축에서 칠각형 평면도는 드물지만, 독일 슈타트하겐의 에른스트 공작 영묘가 대표적인 예이다.

미국의 많은 경찰 배지는 칠각별 윤곽을 가지고 있다.

태국에서는 2011년 12월 국왕 라마 9세의 생일을 기념하여 세계 최초의 칠각형 우표를 발행했다.

참조

_[1] 간행물 Angle trisection, the heptagon, and the triskaidecagon p. 186 (Fig.1) –187 http://apollonius.ma[...] 1988-03
_[2] 간행물 Abu'l-Jūd's Answer to a Question of al-Bīrūnī Concerning the Regular Heptagon https://www.jphogend[...]
_[3] 문서 The Polygons of Albrecht Dürer-1525, The Regular Heptagon https://arxiv.org/ft[...]
_[4] 웹사이트 Heptagon https://www.geogebra[...] 2024-01-20
_[5] 서적 The Symmetries of Things
_[6] 서적 Point group character tables and related data https://books.google[...] Cambridge University Press 1972
_[7] 간행물 Some Collinearities in the Heptagonal Triangle http://forumgeom.fau[...] 2016
_[8] 간행물 The heptagonal triangle 1973-01
_[9] 웹사이트 Heptagon https://polytope.mir[...] miraheze.org 2024-01-20
_[10] 간행물 Pessimal packing shapes
_[11] 웹사이트 Trigonometry Angles--Pi/7
_[12] 문서 このことを、内角あるいは中心角が整数度にならないことと結び付けるのは、初学者にありがちな誤解である。
_[13] 서적 ガロワ理論日本評論社
_[14] 간행물 2017-07
_[15] 뉴스 タイで七角形の切手発売（バンコク経済新聞） http://bangkok.keiza[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com