아다마르 곱

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 예시
3. 성질
4. 프로그래밍 언어에서의 구현
5. 응용
6. 역사
참조

1. 개요

아다마르 곱은 같은 크기의 두 행렬에서 각 요소별로 곱셈을 수행하는 연산이다. 두 행렬의 아다마르 곱은 교환, 결합, 분배 법칙을 따르며, 모든 성분이 1인 행렬은 아다마르 곱의 항등원 역할을 한다. 아다마르 곱은 슈어-오펜하임 부등식과 같은 중요한 성질을 가지며, JPEG 압축, 이미지 처리, 기계 학습, 통계 분석 등 다양한 분야에 응용된다. 프로그래밍 언어에서는 다양한 방식으로 구현되며, MATLAB, 줄리아, 파이썬, C++, GAUSS, 포트란 등에서 지원된다.

더 읽어볼만한 페이지

행렬론 - 행렬식
행렬식은 정사각 행렬에 대해 정의되는 값으로, 선형 방정식의 해를 구하고 선형 독립성을 확인하며 기저의 방향과 부피를 계산하는 데 사용되며, 가우스 소거법 등의 계산 기법과 가역성 판단, 고유값 연관성 등의 성질을 갖는다.
행렬론 - 행렬 분해
행렬 분해는 주어진 행렬을 특정 성질을 갖는 여러 행렬의 곱으로 표현하는 방법으로, 수치 해석에서 행렬 알고리즘 구현 및 선형 연립 방정식 해를 구하거나 행렬 특성 분석에 활용되며 LU 분해, QR 분해, 특잇값 분해 등이 있다.
이항연산 - 뺄셈
뺄셈은 두 수의 관계를 나타내는 연산으로, 덧셈의 역연산이며, 피감수에서 감수를 빼는 연산으로 차를 구하고, 반교환법칙과 결합 법칙은 성립하지 않으며, 다양한 계산 방법과 함께 여러 분야에서 활용된다.
이항연산 - 나눗셈
나눗셈은 하나의 수를 다른 수로 나누어 몫과 나머지를 구하는 기본적인 산술 연산이다.
행렬 - 스핀 (물리학)
스핀은 양자역학적 각운동량으로, 양자화된 값을 가지며 자기 쌍극자 모멘트를 유발하여 다양한 분야에 응용되고 스핀트로닉스 기술 발전에 기여하지만, 전자의 스핀 기원은 아직 완전히 밝혀지지 않았다.
행렬 - 파울리 행렬
파울리 행렬은 양자역학에서 스핀을 나타내는 데 사용되는 에르미트 행렬이자 유니타리 행렬로, 행렬식은 -1이고 대각합은 0이며, 리 대수의 생성원이자 파울리 벡터로 정의되어 다양한 물리학 분야에서 활용된다.

아다마르 곱
개요
이름	아다마르 곱
다른 이름	Schur 곱 (Schur product) 요소별 곱 (element-wise product) 점별 곱 (pointwise product) 성분별 곱 (entrywise product)
분야	선형대수학
정의
정의	두 행렬의 같은 위치의 요소끼리 곱하는 연산
표기법	A ∘ B A ⊙ B A ⊛ B A ◦ B
조건	두 행렬의 크기가 같아야 함
예시
예시	행렬 A와 B의 아다마르 곱은 다음과 같음.
아다마르 곱 예시
속성
교환 법칙	성립 (A ∘ B = B ∘ A)
결합 법칙	성립 (A ∘ (B ∘ C) = (A ∘ B) ∘ C)
분배 법칙	성립 (A ∘ (B + C) = A ∘ B + A ∘ C)
항등원	모든 성분이 1인 행렬
크로네커 곱과의 관계	(A ⊗ B) ∘ (C ⊗ D) = (A ∘ C) ⊗ (B ∘ D)
콤팩트 형식	vec(A ∘ B) = Diag(vec(A)) vec(B)
활용
활용 분야	이미지 압축 손실 압축 알고리즘 신경망
참고
주의사항	일반적인 행렬 곱셈과는 다름

2. 정의

환의 성분을 갖는, 같은 크기 $m\times n$ 의 두 행렬 $M, N\in\operatorname{Mat}(m,n;R)$ 이 주어졌을 때, $M$ 과 $N$ 의 아다마르 곱은 다음과 같이 정의된다.^[2]

: $M\bigcirc N=\begin{pmatrix}M_{11}N_{11}&M_{12}N_{12}&\dotsm&M_{1n}N_{1n}\\M_{21}N_{21}&M_{22}N_{22}&&M_{2n}N_{2n}\\\vdots&&\ddots&\vdots\\M_{m1}N_{m1}&M_{m2}N_{m2}&\dotsm&M_{mn}N_{mn}\end{pmatrix}\in\operatorname{Mat}(m,n;R)$

즉, 두 행렬의 아다마르 곱은 각 성분별 곱으로 정의된다. 아다마르 곱은 $A \odot B$ (또는 $A \circ B$ )^[3]^[4]^[5]로 표기하며, $(A \odot B)_{ij} = (A)_{ij} (B)_{ij}$ 와 같이 나타낼 수 있다.

크기가 다른 두 행렬에 대해서는 아다마르 곱이 정의되지 않는다.

2. 1. 예시

2 × 3 행렬 두 개의 아다마르 곱은 다음과 같다.^[2]

:

\begin{bmatrix}2 & 3 & 1 \\0 & 8 & -2\end{bmatrix} \circ \begin{bmatrix}3 & 1 & 4 \\7 & 9 & 5\end{bmatrix} = \begin{bmatrix}2 \times 3 & 3 \times 1 & 1 \times 4 \\0 \times 7 & 8 \times 9 & -2 \times 5\end{bmatrix} = \begin{bmatrix}6 & 3 & 4 \\0 & 72 & -10\end{bmatrix}

3 × 3 행렬 '''A''' = (a_i,j)와 3 × 3 행렬 '''B''' = (b_i,j)의 아다마르 곱은 다음과 같다.

:

\begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{bmatrix} \circ\begin{bmatrix} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33} \end{bmatrix} =\begin{bmatrix} a_{11}\, b_{11} & a_{12}\, b_{12} & a_{13}\, b_{13}\\ a_{21}\, b_{21} & a_{22}\, b_{22} & a_{23}\, b_{23}\\ a_{31}\, b_{31} & a_{32}\, b_{32} & a_{33}\, b_{33} \end{bmatrix}

3. 성질

아다마르 곱은 교환 법칙, 결합 법칙, 덧셈에 대한 분배 법칙을 만족한다.^[6] 즉, 임의의 행렬 $A, B, C$ 와 스칼라 $k$ 에 대해 다음이 성립한다.

: $A \odot B = B \odot A$

: $A \odot (B \odot C) = (A \odot B) \odot C$

: $A \odot (B + C) = A \odot B + A \odot C$

: $\left(kA\right) \odot B = A \odot \left(kB\right) = k\left(A \odot B\right)$

: $A \odot 0 = 0 \odot A = 0$

모든 성분이 1인 행렬은 아다마르 곱의 항등원이 된다.^[6] 이는 주 대각선의 요소만 1인 일반 행렬 곱셈에서의 항등 행렬과는 다르다. 행렬의 모든 성분이 가역원이라면, 아다마르 곱에 대한 역원을 갖는다.

두 대칭 행렬의 아다마르 곱은 대칭 행렬이 된다. 두 복소수 에르미트 행렬의 아다마르 곱은 에르미트 행렬이 된다. 아다마르 곱은 크로네커 곱의 주요 부분 행렬이다.^[8]^[9]^[10]

3. 1. 슈어-오펜하임 부등식

두 양의 준정부호 에르미트 행렬

M,N\in\operatorname{Mat}(n,n;\mathbb C)

이 주어졌을 때, '''슈어-오펜하임 부등식'''(Schur–Oppenheim inequality^영어)에 따르면 다음이 성립한다.

$M\bigcirc N$ 은 역시 양의 준정부호 에르미트 행렬이다.
$\det (M\bigcirc N)\ge \left(\prod_{i=1}^n\prod_{j=1}^nM_{ij}\right)\det N\ge\det (MN)$

두 양의 반정부호 행렬의 아다마르 곱은 양의 반정부호 행렬이다.^[2]^[14] 이는 러시아 수학자 이사히 슈어의 이름을 딴 슈어 곱 정리로 알려져 있다.^[6] 두 양의 반정부호 행렬

A

와

B

에 대해, 아다마르 곱의 행렬식이 각 행렬의 행렬식의 곱보다 크거나 같다는 것도 알려져 있다.^[14]

:

\det(A \circ B) \ge \det(A) \det(B)

3. 2. 벡터와의 관계

벡터 x와 y, 그리고 이 벡터들을 주 대각선으로 하는 해당 대각 행렬 및 에 대해 다음 항등식이 성립한다.^[7]

:

\mathbf{x}^* (A \odot B)\mathbf{y} = \operatorname{tr}\left({D}_\mathbf{x}^* A {D}_\mathbf{y} {B}^\mathsf{T}\right)

여기서 는 의 켤레 전치를 나타낸다. 특히, 1의 벡터를 사용하면, 아다마르 곱의 모든 요소의 합이 의 대각합임을 보여준다. 여기서 위첨자 T는 전치 행렬을 나타낸다. 즉,

:

\operatorname{tr}\left(AB^{\mathsf T}\right) = \mathbf{1}^\mathsf{T}\left(A\odot B\right)\mathbf{1}

이다.

정사각 행렬 및 에 대한 관련 결과는 아다마르 곱의 행 합이 의 대각 요소라는 것이다.^[14]

:

\sum_i (A \odot B)_{ij} = \left(B^\mathsf{T} A\right)_{jj} = \left(AB^\mathsf{T}\right)_{ii}.

마찬가지로,

:

\left(\mathbf{y}\mathbf{x}^*\right) \odot A = {D}_\mathbf{y} A {D}_\mathbf{x}^*

또한 아다마르 행렬-벡터 곱은 다음과 같이 표현할 수 있다:

:

(A \odot B) \mathbf{y} = \operatorname{diag}\left( A D_\mathbf{y} B^\mathsf{T} \right)

여기서

\operatorname{diag}(M)

은 행렬 의 대각선에서 형성된 벡터이다.

두 벡터

\mathbf a

와

\mathbf b

의 아다마르 곱은 다른 벡터에 의한 한 벡터의 해당 대각 행렬의 행렬 곱셈과 동일하다.

:

\mathbf a \odot \mathbf b = D _{\mathbf a} \mathbf b = D _{\mathbf b} \mathbf a

벡터를 대각 행렬로 변환하는

\operatorname{diag}

연산자(operator)는 아다마르 곱을 사용하여 다음과 같이 표현할 수 있다.

:

\operatorname{diag}(\mathbf{a}) = (\mathbf{a} \mathbf{1}^T) \odot I

여기서

\mathbf{1}

은 요소가

1

인 상수 벡터이고

I

는 항등 행렬이다.

3. 3. 다른 연산과의 관계

아다마르 곱은 (가환환에서 작업할 때) 교환 가능하고 결합적이며 덧셈에 대해 분배적이다. 즉, ''A'', ''B'', ''C''가 동일한 크기의 행렬이고 ''k''가 스칼라일 경우:^[6]

::

\begin{align}A \odot B &= B \odot A, \\A \odot (B \odot C) &= (A \odot B) \odot C, \\A \odot (B + C) &= A \odot B + A \odot C, \\\left(kA\right) \odot B &= A \odot \left(kB\right) = k\left(A \odot B\right), \\A \odot 0 &= 0 \odot A = 0.\end{align}

두 행렬의 아다마르 곱에 대한 항등 행렬은 모든 요소가 1인 행렬이다. 이는 주 대각선의 요소만 1인 일반 행렬 곱셈에서의 항등 행렬과 다르다. 또한 아다마르 곱에서 행렬은 요소 중 0이 아닌 경우에만 역행렬을 갖는다.^[6]
벡터 $\mathbf{x}$ 와 $\mathbf{y}$ 및 이러한 벡터를 주 대각선으로 하는 해당 대각 행렬 $D_\mathbf{x}$ 및 $D_\mathbf{y}$ 에 대해 다음 항등식이 성립한다.^[7]

::

\mathbf{x}^* (A \odot B)\mathbf{y} = \operatorname{tr}\left({D}_\mathbf{x}^* A {D}_\mathbf{y} {B}^\mathsf{T}\right),

: 여기서

\mathbf{x}^*

는

\mathbf{x}

의 켤레 전치를 나타낸다. 특히, 1의 벡터를 사용하여, 이는 아다마르 곱의 모든 요소의 합이

AB^\mathsf{T}

의 대각합임을 보여준다. 여기서 위첨자 T는 전치 행렬을 나타낸다. 즉,

::

\operatorname{tr}\left(AB^{\mathsf T}\right) = \mathbf{1}^\mathsf{T}\left(A\odot B\right)\mathbf{1}

이다.

: 정사각 행렬

A

및

B

에 대한 관련 결과는 아다마르 곱의 행 합이

AB^\mathsf{T}

의 대각 요소라는 것이다.^[14]

::

\sum_i (A \odot B)_{ij} = \left(B^\mathsf{T} A\right)_{jj} = \left(AB^\mathsf{T}\right)_{ii}.

: 마찬가지로,

::

\left(\mathbf{y}\mathbf{x}^*\right) \odot A = {D}_\mathbf{y} A {D}_\mathbf{x}^*

: 또한 아다마르 행렬-벡터 곱은 다음과 같이 표현할 수 있다:

::

(A \odot B) \mathbf{y} = \operatorname{diag}\left( A D_\mathbf{y} B^\mathsf{T} \right)

: 여기서

\operatorname{diag}(M)

은 행렬

M

의 대각선에서 형성된 벡터이다.

아다마르 곱은 크로네커 곱의 주요 부분 행렬이다.^[8]^[9]^[10]
$D$ 와 $E$ 가 대각 행렬이면 ^[12]

::

\begin{align}D (A \odot B) E &= (D A E) \odot B    = (D A) \odot (B E) \\&=  (AE) \odot (D B) =    A \odot (D B E).\end{align}

두 벡터 $\mathbf{a}$ 와 $\mathbf{b}$ 의 아다마르 곱은 다른 벡터에 의한 한 벡터의 해당 대각 행렬의 행렬 곱셈과 동일하다.

::

\mathbf{a} \odot \mathbf{b} = D _{\mathbf{a}} \mathbf{b} = D _{\mathbf{b}} \mathbf{a}

벡터를 대각 행렬로 변환하는 연산자 $\operatorname{diag}$ 는 아다마르 곱을 사용하여 다음과 같이 표현할 수 있다.

::

\operatorname{diag}(\mathbf{a}) = (\mathbf{a} \mathbf{1}^T) \odot I

: 여기서

\mathbf{1}

은 요소가

1

인 상수 벡터이고

I

는 항등 행렬이다.

아다마르 곱과 다른 행렬 곱 연산자와의 관계는 다음과 같다.

만약 $\otimes$ 가 크로네커 곱이고, $A$ 가 $C$ 와, $B$ 가 $D$ 와 같은 차원을 가진다고 가정하면, 다음이 성립한다.

::

(A \otimes B) \odot (C \otimes D) = (A \odot C) \otimes (B \odot D) .

만약 $\bull$ 이 페이스-분할 곱이라면,^[13] 다음이 성립한다.

::

(A \bull B) \odot (C \bull D) = (A \odot C) \bull (B \odot D).

만약 $\ast$ 가 열별 카트리-라오 곱이라면, 다음이 성립한다.

::

(A \bull B)(C \ast D) = (A C) \odot (B D).

4. 프로그래밍 언어에서의 구현

MATLAB에서 아다마르 곱은 "점 곱"으로 표시되며, `a .* b` 또는 `times(a, b)` 함수 호출로 나타낸다.^[18] `a .^ b` 및 `a ./ b`와 같은 유사한 점 연산자도 사용 가능하다.^[19]

줄리아는 MATLAB과 유사하게 아다마르 곱을 `a .* b`로 표시하며, "브로드캐스트 곱셈"이라고 한다. 다른 연산자도 요소별로 정의되어, 아다마르 거듭제곱은 `a .^ b`를 사용한다.^[20]

파이썬은 기본 배열 지원이 없어 표기법이 일관되지 않다. NumPy 수치 라이브러리는 아다마르 곱을 `a*b` 또는 `a.multiply(b)`로 해석하고, 행렬 곱은 `a@b` 또는 `a.matmul(b)`를 사용한다. SymPy 기호 라이브러리에서는 `array` 객체의 곱셈이 `a*b` 또는 `a@b`로 행렬 곱을 생성하며, 아다마르 곱은 `a.multiply_elementwise(b)` 메서드 호출을 통해 얻을 수 있다.^[22]

C++에서는 Eigen 라이브러리가 `Matrix` 클래스에 대한 `cwiseProduct` 멤버 함수(`a.cwiseProduct(b)`)를 제공하며, Armadillo 라이브러리는 연산자 `%`를 사용해 `a % b`로 표현한다. (`a * b`는 행렬 곱)

GAUSS와 HP Prime에서는 이 연산을 ''배열 곱셈''이라고 한다.

포트란, R, APL, J 및 울프람 언어 (Mathematica)에서 곱셈 연산자 `*` 또는 `×`는 아다마르 곱을 적용한다. 반면 행렬 곱은 각각 `matmul`, `%*%`, `+.×`, `+/ .*` 및 `.`을 사용하여 작성한다. R 패키지 [https://cran.r-project.org/web/packages/matrixcalc/matrixcalc.pdf matrixcalc]는 숫자 행렬 또는 벡터의 아다마르 곱에 대한 함수 `hadamard.prod()`를 제공한다.^[23]

프로그래밍 언어별 아다마르 곱 표기법
프로그래밍 언어	아다마르 곱 표기	행렬 곱 표기
MATLAB	`a .* b` 또는 `times(a, b)`	`a * b`
줄리아	`a .* b`	해당사항 없음
NumPy	`a*b` 또는 `a.multiply(b)`	`a@b` 또는 `a.matmul(b)`
SymPy	`a.multiply_elementwise(b)`	`a*b` 또는 `a@b`
Eigen (C++)	`a.cwiseProduct(b)`	해당사항 없음
Armadillo (C++)	`a % b`	`a * b`
GAUSS	배열 곱셈	해당사항 없음
HP Prime	배열 곱셈	해당사항 없음
포트란	`*`	`matmul`
R	`*` 또는 `hadamard.prod()`	`%*%`
APL	`×`	`+.×`
J	`*`	`+/ .*`
울프람 언어 (Mathematica)	`*` 또는 `×`	`.`

5. 응용

아다마르 곱은 JPEG와 같은 손실 압축 알고리즘에 사용된다. 디코딩 단계는 항목별 곱셈, 즉 아다마르 곱을 포함한다.

이미지 처리에서 아다마르 연산자는 이미지 영역을 향상시키거나, 억제하거나, 마스킹하는 데 사용할 수 있다. 하나의 행렬은 원본 이미지를 나타내고, 다른 행렬은 가중치 또는 마스킹 행렬 역할을 한다.

이는 기계 학습 문헌에서 GRU 또는 LSTM과 같은 순환 신경망의 아키텍처를 설명하는 데 사용된다.^[24]

또한 임의 벡터와 행렬의 통계적 특성을 연구하는 데 사용된다.^[25]^[26]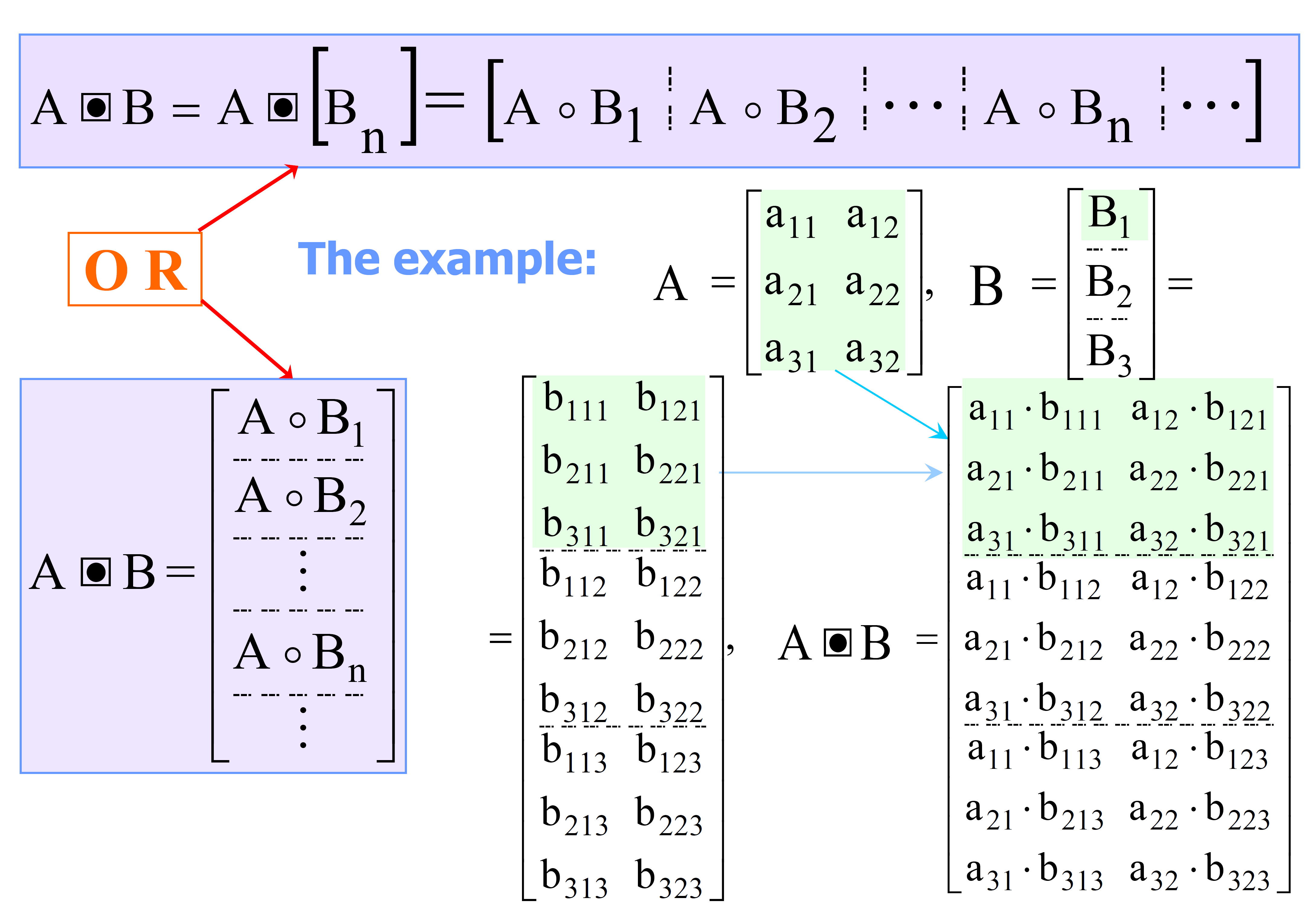

V. 슬류사르의 정의에 따르면, ''p''×''g'' 행렬

{A}

와 ''p''×''g'' 블록(

{B} = [B_n]

)을 가진 ''n''차원 행렬

{B}

(''n'' > 1)의 침투 면 곱은 다음과 같은 형태의

{B}

크기의 행렬이다:^[27]

:

{A} [\circ] {B} =\left[\begin{array} { c | c | c | c }{A} \circ {B}_1 & {A} \circ {B}_2 & \cdots & {A} \circ {B}_n\end{array}\right].

6. 역사

"아다마르 곱"이라는 용어는 자크 아다마르의 이름을 딴 것이다.

이사이 슈어는 1911년에 $\det (M\bigcirc N)\ge \det (MN)$ 을 증명하였으며,^[32] Alexander Oppenheim|알렉산더 오펜하임^영어(1903~1997)이 1930년에 이를 개량하였다.^[33]

참조

_[1] 논문 The norm of the Schur product operation
_[2] 웹사이트 The Hadamard Product http://buzzard.ups.e[...] 2020-09-06
_[3] 웹사이트 Hadamard product - Machine Learning Glossary https://machinelearn[...]
_[4] 웹사이트 linear algebra - What does a dot in a circle mean? https://math.stackex[...]
_[5] 웹사이트 Element-wise (or pointwise) operations notation? https://math.stackex[...]
_[6] 웹사이트 The Hadamard Product http://buzzard.ups.e[...] 2012-01-02
_[7] 서적 Matrix analysis Cambridge University Press 2012
_[8] 논문 Hadamard, Khatri-Rao, Kronecker and other matrix products
_[9] 논문 Matrix differential calculus with applications in the multivariate linear model and its diagnostics
_[10] 논문 Professor Heinz Neudecker and matrix differential calculus 2023
_[11] 논문 On an eigenvalue inequality involving the Hadamard product 2017-02
_[12] 웹사이트 Project http://buzzard.ups.e[...] buzzard.ups.edu 2019-12-18
_[13] 논문 End products in matrices in radar applications. http://slyusar.kiev.[...]
_[14] 논문 Hadamard Products and Multivariate Statistical Analysis
_[15] 논문 Hadamard inverses, square roots and products of almost semidefinite matrices
_[16] 웹사이트 Supplementary Material: Tensor Displays: Compressive Light Field Synthesis using Multilayer Displays with Directional Backlighting http://web.media.mit[...]
_[17] 서적 Object Detection and Recognition in Digital Images: Theory and Practice https://books.google[...] John Wiley & Sons
_[18] 웹사이트 MATLAB times function https://www.mathwork[...]
_[19] 웹사이트 Array vs. Matrix Operations https://www.mathwork[...]
_[20] 웹사이트 Vectorized "dot" operators https://docs.juliala[...] 2024-01-31
_[21] 웹사이트 Dot Syntax for Vectorizing Functions https://docs.juliala[...] 2024-01-31
_[22] 웹사이트 Common Matrices — SymPy 1.9 documentation https://docs.sympy.o[...]
_[23] 웹사이트 Matrix multiplication https://cran.r-proje[...] The R Project for Statistical Computing 2013-08-24
_[24] arXiv Long Short-Term Memory Based Recurrent Neural Network Architectures for Large Vocabulary Speech Recognition 2014-02-05
_[25] 논문 The Hadamard product and some of its applications in statistics
_[26] 논문 Some statistical properties of Hadamard products of random matrices
_[27] 논문 A Family of Face Products of Matrices and its properties http://slyusar.kiev.[...] 1998-03-13
_[28] 논문 HyperNetworks. 2017
_[29] 웹사이트 The Hadamard Product http://buzzard.ups.e[...] 2012-01-02
_[30] 서적
_[31] 서적
_[32] 저널 http://resolver.sub.[...]
_[33] 저널

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com