온음
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
온음은 음정의 한 종류로, 순정률과 같은 음률 체계에서 두 가지 크기로 나타난다. 더 넓은 음정을 장음 또는 큰 음(9:8 비율)이라 하고, 더 좁은 음정을 단음 또는 작은 음(10:9 비율)이라고 부른다. 이 두 음정의 크기 차이는 신토닉 콤마와 같다. 일부 균등 분할 음계에서도 두 가지 크기의 장2도를 생성하며, 15-ET, 22-ET, 34-ET 등이 이에 해당한다. 12 평균율, 피타고라스 조율법 등에서는 모든 장2도가 동일한 크기를 가진다. 피타고라스 조율법 음악 이론에서 에포그도온은 9:8의 비율을 가진 음정을 의미한다.
더 읽어볼만한 페이지
- 음정 - 옥타브
옥타브는 음악에서 주파수 비율 2:1로 표현되는 음정 간격으로, 특정 음과 그 두 배 또는 절반 주파수를 갖는 다른 음 사이의 관계를 나타내며, 옥타브 등가성 개념에 따라 여러 문화권에서 동등하게 인식된다. - 음정 - 센트 (음악)
센트는 음악에서 음높이 간격을 나타내는 로그 척도 단위로, 두 주파수 비율 측정에 사용되며 균등 조율에서 반음은 100센트, 옥타브는 1200센트에 해당하고 청각적 현상과도 관련된다. - 토막글 틀에 과도한 변수를 사용한 문서 - 전향
전향은 종교적 개종이나 노선 변경을 의미하며, 근대 이후 정치적 이념 변화를 지칭하는 용어로 확장되어 개인의 신념 변화, 정치적 압력 등 다양한 요인으로 발생하며, 사회주의·공산주의로부터의 전향, 전향 문학, 냉전 시대 이후의 전향 현상 등을 폭넓게 논의한다. - 토막글 틀에 과도한 변수를 사용한 문서 - 포토마스크
포토마스크는 반도체, 디스플레이, 인쇄 회로 기판 제조 시 웨이퍼에 회로 패턴을 전사하는 마스크로, 기술 발전을 거듭하며 융용 실리카 기판과 금속 흡수막을 사용하고 위상 천이 마스크, EUV 마스크 등의 고급 기술이 개발되어 반도체 미세화에 기여하고 있지만, 높은 제작 비용과 기술적 어려움은 해결해야 할 과제이다. - 토론 이름공간 토막글 - 전향
전향은 종교적 개종이나 노선 변경을 의미하며, 근대 이후 정치적 이념 변화를 지칭하는 용어로 확장되어 개인의 신념 변화, 정치적 압력 등 다양한 요인으로 발생하며, 사회주의·공산주의로부터의 전향, 전향 문학, 냉전 시대 이후의 전향 현상 등을 폭넓게 논의한다. - 토론 이름공간 토막글 - 포토마스크
포토마스크는 반도체, 디스플레이, 인쇄 회로 기판 제조 시 웨이퍼에 회로 패턴을 전사하는 마스크로, 기술 발전을 거듭하며 융용 실리카 기판과 금속 흡수막을 사용하고 위상 천이 마스크, EUV 마스크 등의 고급 기술이 개발되어 반도체 미세화에 기여하고 있지만, 높은 제작 비용과 기술적 어려움은 해결해야 할 과제이다.
| 온음 | |
|---|---|
| 음정 정보 | |
| 주요 음정 이름 | 장2도 |
| 다른 이름 | 온음, 온전한 단계 |
| 약어 | M2 |
| 반음 수 | 2 |
| 음정 종류 | 2 |
| 순정 음정 | 9:8 또는 10:9 |
| 평균율 (센트) | 200 |
| 순정률 (센트) | 204 또는 182 |
| 소리 정보 | |
| 추가 정보 | |
| 설명 | 으뜸음(키노트)에서 위쪽 방향으로 두 번째, 세 번째, 여섯 번째, 일곱 번째 스케일 차수까지의 음정은 장음이라고 불린다. |
2. 장2도와 음률 체계
순정률과 같은 음률 시스템에서는 장2도가 두 가지 크기로 나타나는데, 이 중 더 넓은 것을 '''장음''' 또는 '''큰 음'''이라고 부르고, 더 좁은 것을 '''단음''' 또는 '''작은 음'''이라고 부른다. 장음과 단음의 크기 차이는 신토닉 콤마 하나와 같다(약 21.51 센트).[11]
이러한 음률 시스템에서는 장음보다 더 넓은 종류의 완전음이 존재하는데, 2개의 반음 간격으로 이루어진 이 음정은 256:225 비율을 가지며, 감3도라고 불린다.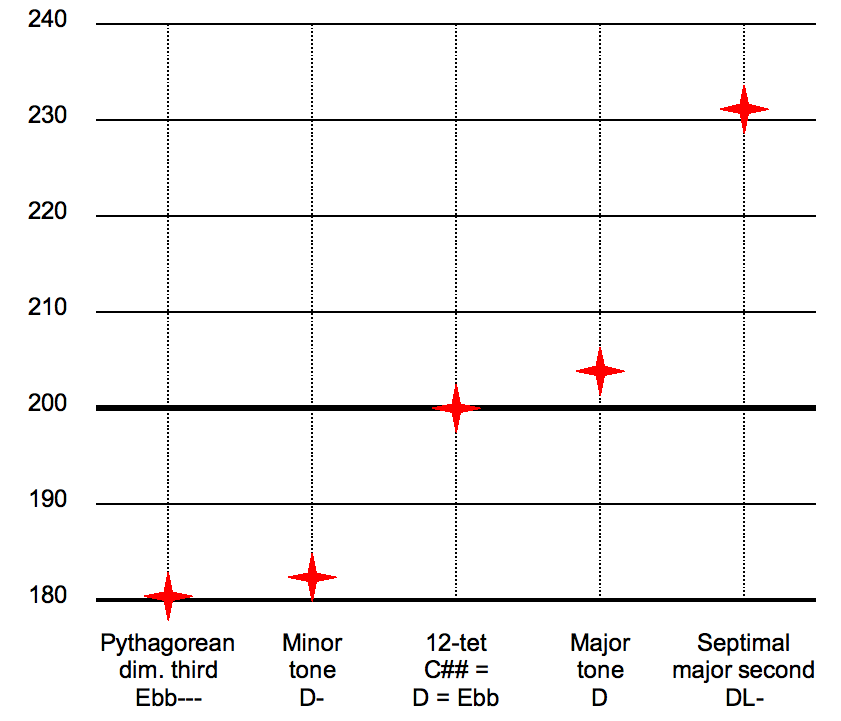
장2도가 하나의 크기만 존재하는 시스템에서는 '큰 음'과 '작은 음'(또는 '장음'과 '단음')이라는 용어가 다른 의미로 사용되는 경우는 드물다. 이 용어들은 보통 '장2도'(M2)와 '감3도'(d3)라고 불리는 두 가지 종류의 완전음을 나타내는 데 사용된다. 마찬가지로, 장반음과 단반음은 '단2도'(m2)와 '증1도'(A1), 또는 '온음계적' 및 '반음계적 반음'이라고 불린다.
'장'과 '단'이라는 용어의 일반적인 사용과는 달리, 장2도와 감3도는 ''동일한'' 수의 반음을 포함한다. 둘 다 2개의 반음을 포함하는 반면, 장3도 (4 반음)와 단3도 (3 반음)는 1개의 반음 차이를 보인다. 따라서 모호성을 피하기 위해 장2도와 감3도를 '큰 음'과 '작은 음'이라고 부르는 것이 더 바람직하다.
두 개의 장음은 디톤과 같다.
2. 1. 순정률과 장2도
순정률과 같은 음률 시스템에서는 장2도가 두 가지 크기로 나타난다. 이 중 더 넓은 것을 '''장음''' 또는 '''큰 음'''이라고 부르고, 더 좁은 것을 '''단음''' 또는 '''작은 음'''이라고 부른다. 장음과 단음의 크기 차이는 신토닉 콤마 하나와 같다(약 21.51 센트).장음은 9:8 음정[11]이며, 다른 음률 시스템에서도 이와 유사하게 나타난다. 단음은 10:9 비율[11]이다. 장음은 배음열에서 8번째 배음과 9번째 배음 사이의 음정으로, 단음은 9번째 배음과 10번째 배음 사이의 음정으로 파생될 수 있다. 10:9 단음은 C 장음계에서 D와 E 사이, G와 A 사이에 나타나며, 9:8보다 "더 날카로운 불협화음"이다.[12][13] 9:8 장음은 C 장음계에서 C와 D 사이, F와 G 사이, A와 B 사이에 나타난다.[12] 이 9:8 음정은 피타고라스 학파에 의해 에포그돈('1/8 추가'를 의미)이라고 명명되었다.
2. 2. 평균율과 장2도
순정률과 같은 음률 시스템에서는 장2도가 두 가지 크기로 나타나는데, 이 중 더 넓은 것을 '''장음''' 또는 '''큰 음'''이라고 부르고, 더 좁은 것을 '''단음''' 또는 '''작은 음'''이라고 부른다. 장음과 단음의 크기 차이는 신토닉 콤마 하나와 같다(약 21.51 센트).[11]12 평균율, 피타고라스 조율법, 중간 음조율법(19-ET 및 31-ET 포함)에서는 모든 장2도가 동일한 크기를 가지므로, 큰 음과 작은 음을 구분할 수 없다.
반면, 일부 균등 분할 음계에서는 두 가지 크기의 장2도를 생성하며, 이를 '큰' 음과 '작은' 음(또는 '장음'과 '단음')이라고 부른다. 예를 들어, 15-ET, 22-ET, 34-ET, 41-ET, 53-ET, 72-ET 등이 이에 해당한다.
3. 에포그도온 (Epogdoon)
피타고라스 조율법 음악 이론에서 '''에포그도온'''(ἐπόγδοον|에포그도온grc)은 9:8의 비율을 가진 음정으로, "위에"를 의미하는 접두사 ''epi''-와 "8분의 1"을 의미하는 ''ogdoon''으로 구성되어 "8분의 1을 더한 것"을 의미한다. 예를 들어, 자연수 8과 9는 이러한 관계를 가진다().
플루타르코스에 따르면, 피타고라스 학파는 17이라는 숫자를 싫어했는데, 이는 16을 에포그도온 18로부터 분리하기 때문이다.[14]
에포그도스는 음(tone)에 해당하는 9:8 비율이고, 헤미올리오스는 음악적 5도와 관련된 3:2 비율이며, 에피트리토스는 음악적 4도와 관련된 4:3 비율이다. 에포그도스를 '음'(major second)으로 번역하는 것이 일반적이다.[15]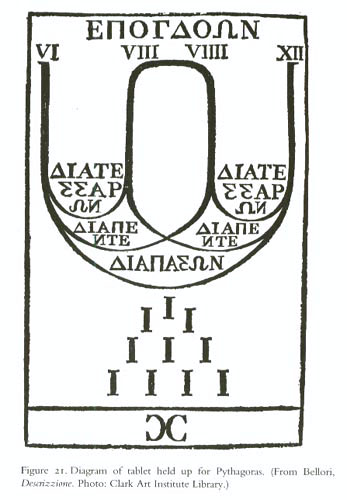
3. 1. 피타고라스와 에포그도온
피타고라스 조율법 음악 이론에서 '''''에포그도온'''''(ἐπόγδοον|에포그도온grc)은 9:8의 비율을 가진 음정이다. 이 단어는 "위에"를 의미하는 접두사 ''epi''-와 "8분의 1"을 의미하는 ''ogdoon''으로 구성되어 있으며, 따라서 "8분의 1을 더한 것"을 의미한다. 예를 들어, 이 관계에서 자연수는 8과 9이다().플루타르코스에 따르면, 피타고라스 학파는 17이라는 숫자를 싫어했는데, 이는 16을 에포그도온 18로부터 분리하기 때문이다.[14]
"에포그도스는 음(tone)에 해당하는 9:8 비율이고, 헤미올리오스는 음악적 5도와 관련된 3:2 비율이며, 에피트리토스는 음악적 4도와 관련된 4:3 비율이다. '''''에포그도스'''''를 '음'(major second)으로 번역하는 것이 일반적이다."[15]
3. 2. 에포그도온과 현대 음악 이론
피타고라스 조율법 음악 이론에서 '''''에포그도온'''''(ἐπόγδοον|에포그도온grc)은 9:8의 비율을 가진 음정이다. 이 단어는 "위에"를 의미하는 접두사 ''epi''-와 "8분의 1"을 의미하는 ''ogdoon''으로 구성되어 있으며, 따라서 "8분의 1을 더한 것"을 의미한다. 예를 들어, 이 관계에서 자연수는 8과 9이다.플루타르코스에 따르면, 피타고라스 학파는 17이라는 숫자를 싫어했는데, 이는 16을 에포그도온 18로부터 분리하기 때문이다.[14]
"에포그도스는 음(tone)에 해당하는 9:8 비율이고, 헤미올리오스는 음악적 5도와 관련된 3:2 비율이며, 에피트리토스는 음악적 4도와 관련된 4:3 비율이다. 에포그도스를 '음'(major second)으로 번역하는 것이 일반적이다."[15]
4. 장2도의 음악적, 문화적 의의
순정률과 같은 음률 시스템에서는 장2도가 두 가지 크기로 나타나는 경우가 있다. 더 넓은 것을 '장음'(또는 '큰 음'), 좁은 것을 '단음'(또는 '작은 음')이라고 부른다. 장음과 단음의 크기 차이는 신토닉 콤마 하나와 같으며, 약 21.51 센트이다.
장음은 9:8 음정,[11] 단음은 10:9 비율이다.[11] 장음은 배음열에서 8번째와 9번째 배음 사이, 단음은 9번째와 10번째 배음 사이에서 파생될 수 있다. C 장음계에서 10:9 단음은 D와 E, G와 A 사이에 나타나며, 9:8 장음보다 "더 날카로운 불협화음"으로 간주된다.[12][13] 9:8 장음은 C와 D, F와 G, A와 B 사이에 나타난다.[12] 이 9:8 음정은 피타고라스 학파에 의해 에포그돈(1/8 추가를 의미)이라고 불렸다.
15-ET, 22-ET, 34-ET, 41-ET, 53-ET, 72-ET 등 일부 균등 분할 음계에서도 두 가지 크기의 장2도가 나타난다. 반면, 12 평균율, 피타고라스 조율법, 중간 음조율법(19-ET 및 31-ET 포함)에서는 모든 장2도가 동일한 크기를 가지므로, 큰 음과 작은 음을 구분할 수 없다.
장2도가 하나의 크기만 존재하는 시스템에서는 '큰 음'과 '작은 음'이라는 용어가 '장2도'(M2)와 '감3도'(d3)를 지칭하는 경우도 있다. 마찬가지로, 장반음과 단반음은 '단2도'(m2)와 '증1도'(A1), 또는 '온음계적' 및 '반음계적 반음'이라고 불리는 경우가 더 일반적이다.
두 개의 장음을 합치면 디톤이 된다.
4. 1. 음악적 표현과 장2도
순정률과 같은 음률 시스템에서는 장2도가 두 가지 크기로 나타나는데, 이 중 더 넓은 것을 '''장음''' 또는 '''큰 음'''이라고 부르고, 더 좁은 것을 '''단음''' 또는 '''작은 음'''이라고 부른다. 장음과 단음의 크기 차이는 신토닉 콤마 하나와 같다(약 21.51 센트).장음은 9:8 음정[11]이며, 다른 음률 시스템에서도 이와 유사하게 나타난다. 단음은 10:9 비율[11]이다. 장음은 배음열에서 8번째 배음과 9번째 배음 사이의 음정으로 파생될 수 있다. 단음은 배음열에서 9번째 배음과 10번째 배음 사이의 음정으로 파생될 수 있다. 10:9 단음은 C 장음계에서 D와 E 사이, G와 A 사이에 나타나며, 9:8보다 "더 날카로운 불협화음"이다.[12][13] 9:8 장음은 C 장음계에서 C와 D 사이, F와 G 사이, A와 B 사이에 나타난다.[12] 이 9:8 음정은 피타고라스 학파에 의해 에포그돈(1/8 추가를 의미)이라고 명명되었다.
이러한 음률 시스템에서는 장음보다 더 넓은 종류의 완전음이 존재한다. 2개의 반음 간격으로 이루어진 이 음정은 256:225 비율을 가지며, 단순히 감3도라고 불린다.
일부 균등 분할 음계에서도 두 가지 크기의 장2도를 생성하며, 이를 '큰' 음과 '작은' 음(또는 '장음'과 '단음')이라고 부른다. 예를 들어, 15-ET, 22-ET, 34-ET, 41-ET, 53-ET, 72-ET 등이 이에 해당한다.
반대로, 12 평균율, 피타고라스 조율법, 중간 음조율법(19-ET 및 31-ET 포함)에서는 모든 장2도가 동일한 크기를 가지므로, 큰 음과 작은 음을 구분할 수 없다.
장2도가 하나의 크기만 존재하는 시스템에서는 '큰 음'과 '작은 음'(또는 '장음'과 '단음')이라는 용어가 다른 의미로 사용되는 경우는 드물다. 즉, 이 용어들은 더 일반적으로, 그리고 더 적절하게 '장2도'(M2)와 '감3도'(d3)라고 불리는 두 가지 종류의 완전음을 나타내는 데 사용된다. 마찬가지로, 장반음과 단반음은 더 자주, 그리고 더 적절하게 '단2도'(m2)와 '증1도'(A1), 또는 '온음계적' 및 '반음계적 반음'이라고 불린다.
'장'과 '단'이라는 용어의 거의 모든 사용법과는 달리, 이 음정들은 ''동일한'' 수의 반음을 포함한다. 둘 다 2개의 반음을 포함하는 반면, 예를 들어 장3도(4 반음)와 단3도(3 반음)는 1개의 반음 차이를 보인다. 따라서 모호성을 피하기 위해 이를 '큰 음'과 '작은 음'이라고 부르는 것이 더 바람직하다.
두 개의 장음은 디톤과 같다.
참조
[1]
서적
How equal temperament ruined harmony : (and why you should care)
https://books.google[...]
W. W. Norton
2008
[2]
서적
Music: In Theory and Practice, Vol. I
Benward, Bruce & Saker, Marilyn
2003
[3]
웹사이트
Whole step – Definition and More from the Free Merriam-Webster Dictionary
http://www.merriam-w[...]
Merriam-webster.com
2015-02-25
[4]
웹사이트
Oxford Dictionaries – Dictionary, Thesaurus, & Grammar
http://www.askoxford[...]
Askoxford.com
2015-02-11
[5]
웹사이트
Whole step | Define Whole step at Dictionary.com
http://dictionary.re[...]
Dictionary.reference.com
2015-02-25
[6]
웹사이트
Whole tone | Define Whole tone at Dictionary.com
http://dictionary.re[...]
Dictionary.reference.com
2015-02-25
[7]
서적
The Complete Idiot's Guide to Music Theory – Michael Miller – Google Books
https://books.google[...]
2015-02-25
[8]
서적
Music Theory For Dummies – Michael Pilhofer, Holly Day – Google Books
https://books.google[...]
2011-02-25
[9]
서적
Lou Harrison
Leta E. Miller, Fredric Lieberman
2006
[10]
서적
Lou Harrison: Selected keyboard and chamber music, 1937–1994
Leta E. Miller, ed.
1988
[11]
간행물
Proceedings of the Royal Society of London, Volume 30
Royal Society (Great Britain)
1880
[12]
문서
Paul, Oscar
Paul, Oscar
1885
[13]
웹사이트
A Manual of Harmony for Use in Music-schools and Seminaries and for Self ... – Oscar Paul – Google Books
https://books.google[...]
2010-05-25
[14]
웹사이트
Plutarch • Isis and Osiris (Part 3 of 5)
https://penelope.uch[...]
Penelope.uchicago.edu
2015-02-25
[15]
웹사이트
Proclus : Commentary on Plato's Timaeus
http://philpapers.or[...]
Philpapers.org
2015-02-25
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
