유클리드 호제법

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 작동 원리
- 3.1. 정수의 경우
- 3.2. 다항식의 경우
4. 확장된 유클리드 호제법
- 4.1. 정수의 경우
- 4.2. 다항식의 경우
5. 응용
6. 계산 복잡도
7. 다른 수 체계로의 확장
8. 같이 보기
참조

1. 개요

유클리드 호제법은 두 정수의 최대공약수를 효율적으로 계산하는 알고리즘이다. 기원전 300년경 유클리드의 저서에 처음 등장하며, 정수, 다항식, 실수 등 다양한 수학적 대상에 적용될 수 있다. 이 알고리즘은 최대공약수를 구하는 데 사용될 뿐 아니라, 베주의 항등식, 디오판토스 방정식, 유한체, 연분수, 정수 인수분해 등 다양한 분야에 응용된다. 유클리드 호제법은 계산 복잡도가 낮아 매우 효율적이며, 확장된 유클리드 호제법은 베주의 항등식의 해를 찾는 데 사용된다.

더 읽어볼만한 페이지

수론 알고리즘 - 고대 이집트 곱셈법
고대 이집트 곱셈법은 두 열을 사용하여 곱셈을 계산하는 방식으로, 첫 번째 수를 2의 거듭제곱으로 분해하고 두 번째 수에 2의 거듭제곱을 곱하는 방법을 사용했으며, 분배 법칙과 수학적 귀납법으로 정확성이 증명되어 현대 사회에도 응용된다.
수론 알고리즘 - 이진 최대공약수 알고리즘
이진 최대공약수 알고리즘은 짝수/홀수 판별, 뺄셈, 비트 시프트 연산을 통해 최대공약수를 구하는 효율적인 알고리즘으로, 두 수가 짝수일 때 2를 공약수로 추출하고 한 수가 짝수일 때 2로 나누는 과정을 반복하며 C 언어, Rust 등 다양한 언어로 구현 가능하고 정수환으로 확장될 수 있다.
에우클레이데스 - 유클리드 정역
유클리드 정역은 나눗셈 연산의 나머지에 대한 조건을 만족하는 유클리드 함수를 갖는 정역으로, 체, 정수환, 가우스 정수 환 등의 예시를 가지며 모든 유클리드 정역은 주 아이디얼 정역이지만 그 역은 성립하지 않고, 대수적 수체의 정수환이 유클리드 정역이 되는지 여부는 중요한 연구 대상이다.
에우클레이데스 - 옥시링쿠스 파피루스 29번
옥시링쿠스 파피루스 29번은 《원론》 제2권의 다섯 번째 명제를 담고 있는 현존하는 가장 오래된 필사본 중 하나로, 고대 그리스 기하학 연구에 중요한 자료이다.

유클리드 호제법
개요
유클리드 호제법의 시각적 표현.
유형	알고리즘
문제	최대공약수
발견자	유클리드
발견 시기	기원전 300년경
작동 방식
입력	두 자연수 a와 b
출력	a와 b의 최대공약수
단계
성능
최악의 경우	O(n), 여기서 n은 더 작은 숫자의 자릿수이다.
응용
사용 분야	기약 분수 만들기 모듈러 역수 찾기 암호학
관련 알고리즘
관련 항목	확장 유클리드 알고리즘

2. 역사

유클리드 호제법은 기원전 300년경 유클리드의 저서 《원론》에 처음 등장한다.^[10]^[11] 하지만, 이 알고리즘은 유클리드 이전에 이미 알려져 있었을 가능성이 크다. 인도와 중국에서도 유클리드 호제법과 유사한 알고리즘이 독립적으로 발견되었으며, 이는 주로 천문학 및 달력 계산에 활용되었다.

19세기에 들어서면서, 유클리드 호제법은 가우스 정수와 같은 새로운 수 체계의 개발에 영향을 주었으며, 대수학의 발전에도 기여하였다.^[59] 현대에는 정수 관계 알고리즘, RSA 암호화 알고리즘 등 다양한 분야에 응용되고 있다.

3. 작동 원리

유클리드 호제법은 주어진 두 수의 최대공약수를 구하는 알고리즘이다. 두 수 a와 b (a > b)의 최대공약수를 구하기 위해 다음과 같은 단계를 거친다.

b가 0이면, a를 출력하고 알고리즘을 종료한다.
a가 b로 나누어 떨어지면, b를 출력하고 알고리즘을 종료한다.
그렇지 않으면, a를 b로 나눈 나머지를 새로운 a에 대입하고, a와 b를 바꾸고 위의 과정을 반복한다.

이 과정은 나머지가 0이 될 때까지 반복되며, 마지막으로 나눈 수가 최대공약수가 된다.

예를 들어 1071과 1029의 최대공약수를 구하는 과정은 다음과 같다.

1071을 1029로 나눈 나머지는 42이다.
1029를 42로 나눈 나머지는 21이다.
42를 21로 나눈 나머지는 0이다.

따라서 최대공약수는 21이다.

이러한 과정은 "n, m에 대해서 나머지 연산을 실시할 수 있다"라는 조건에만 의존하므로, 정수환뿐 아니라 임의의 유클리드 정역에 대해서도 똑같은 과정을 거치면 공약인자를 구할 수 있다.^[15]

유클리드 호제법은 최대공약수를 구하는 대상인 두 정수를 폭과 높이로 설정한 직사각형 내에서 붉은색 사선의 직선을 그리는 과정으로도 표현할 수 있다. 붉은색 사선은 직사각형의 한쪽 구석에서 시작하여 45도 각도로 그려지며, 변에 닿으면 직각으로 반사된다. 직선이 반대편 변에 닿으면, 직전 반사 지점에서 수직으로 선을 그어 직사각형을 두 부분으로 나눈다. 이 과정을 반복하여 더 작은 직사각형을 만들고, 직선이 직사각형의 모서리에 닿으면 알고리즘이 종료된다. 이때 마지막 직사각형의 짧은 변의 길이가 최대공약수가 된다.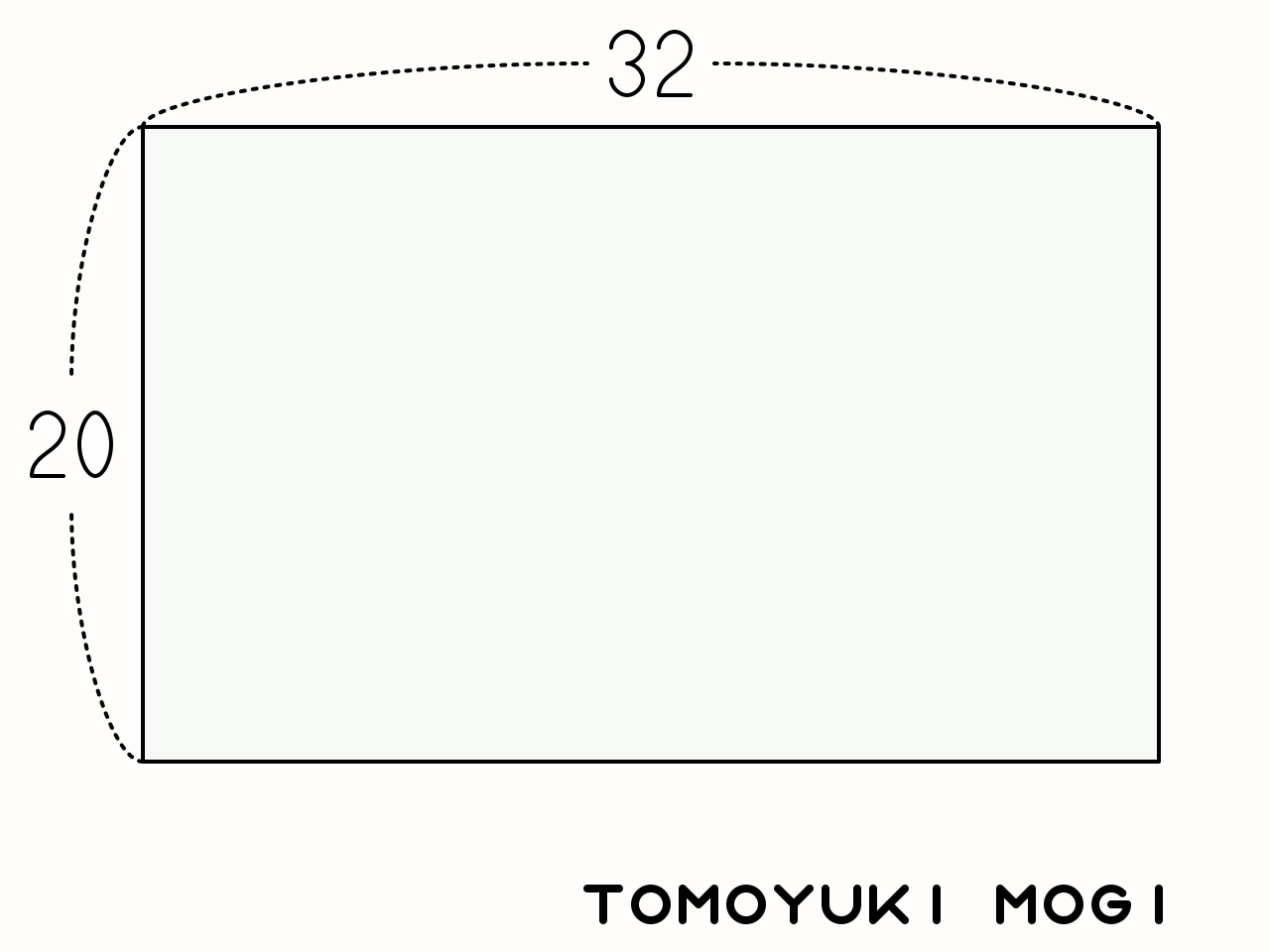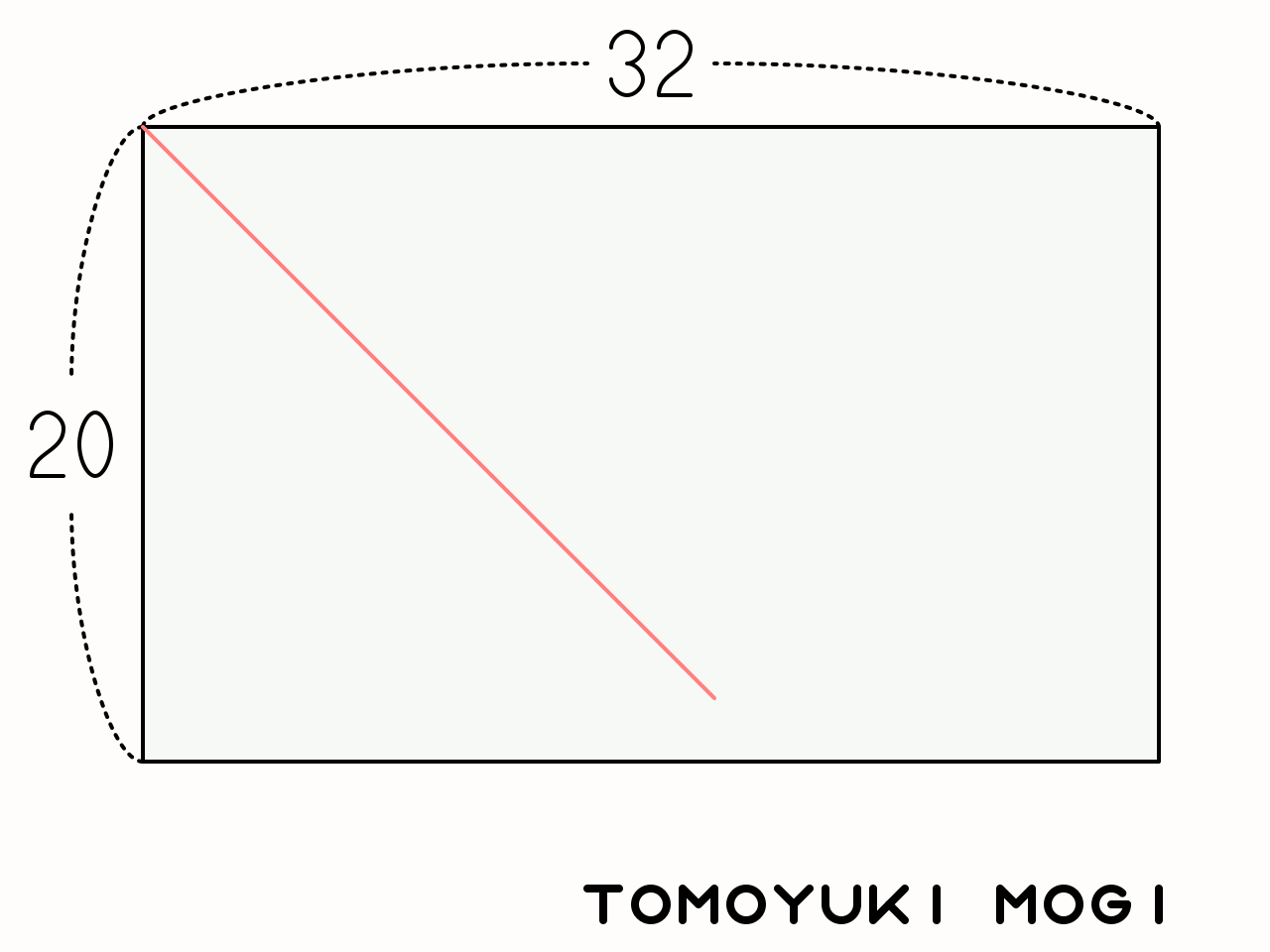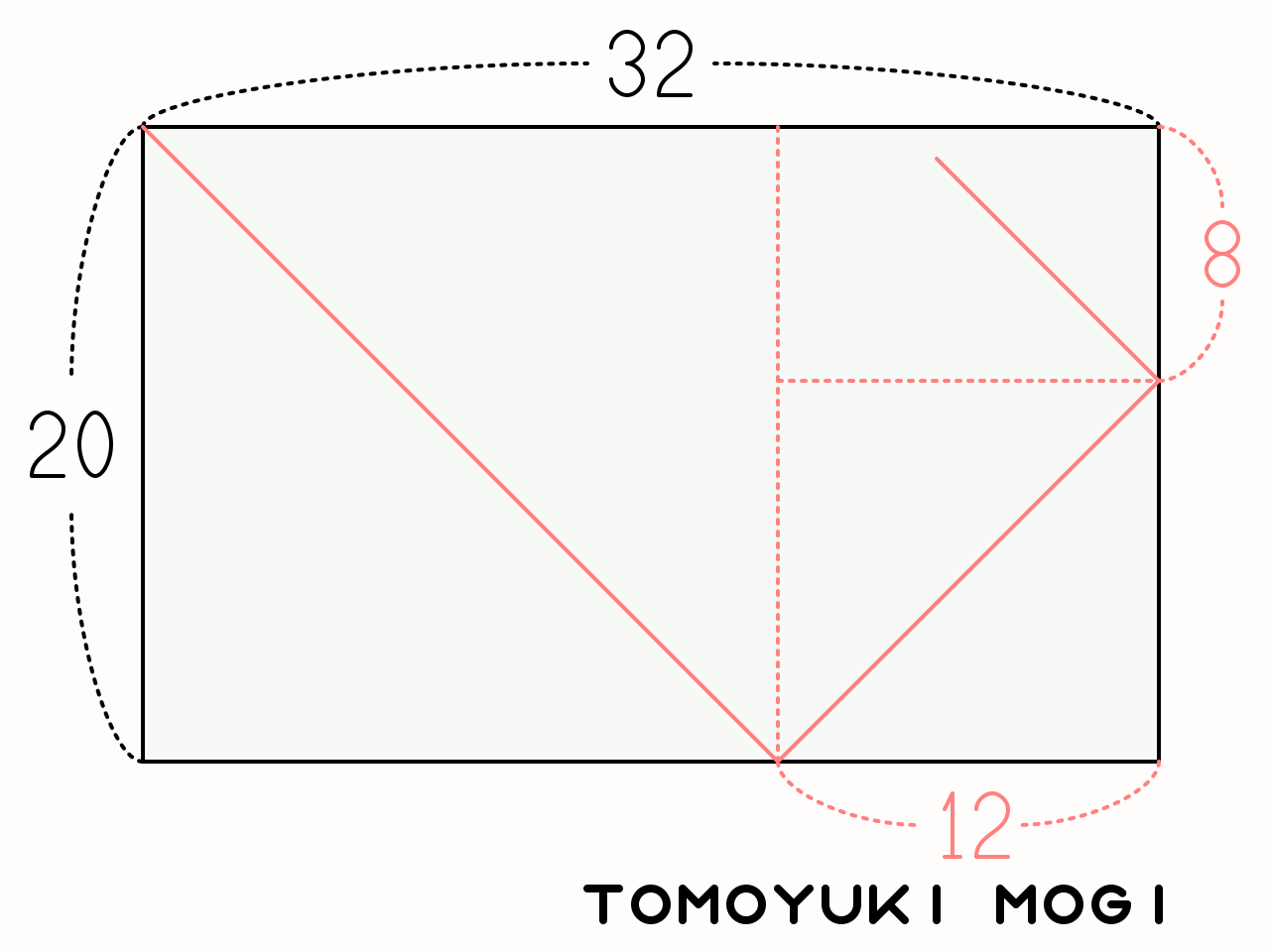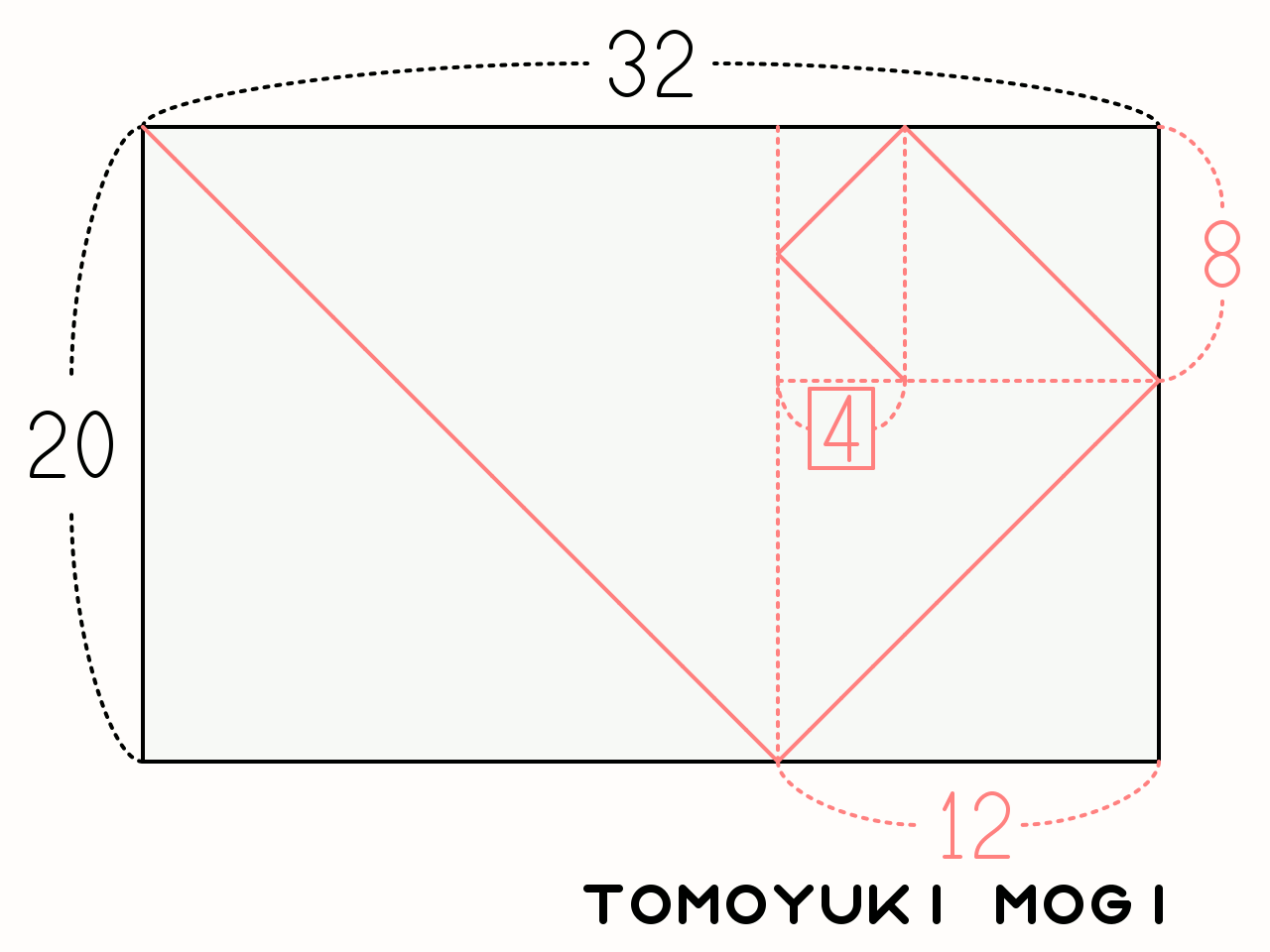

3. 1. 정수의 경우

두 정수 a와 b의 최대공약수는 유클리드 호제법을 통해 다음과 같이 계산될 수 있다.

1071과 1029의 최대공약수를 구하는 과정은 다음과 같다.
* 1071을 1029로 나눈 나머지는 42이다.
* 1029를 42로 나눈 나머지는 21이다.
* 42를 21로 나눈 나머지는 0이다.

따라서, 최대공약수는 21이다.

78696과 19332의 최대공약수를 구하는 과정은 다음과 같다.

'''78696''' ＝ '''19332'''×4 ＋ 1368

19332 ＝ 1368×14 ＋ 180

1368 ＝ 180×7 ＋ 108

180 ＝ 108×1 ＋ 72

108 ＝ 72×1 ＋ 36

72 ＝ 36×2 ＋ 0

따라서, 최대공약수는 36이다.

유클리드 호제법의 정당성은 다음 정리를 통해 증명될 수 있다.

:

a, b \in \mathbb{Z}

이고,

a

를

b

로 나눈 나머지가

r

이라고 하자. (여기서

a\ge b

이고,

r

은

0 \le r < b

인 정수.)

:

\left(a, b\right) = \left(b, r\right).

1071과 1029에 대한 예시를 위와 같은 표현으로 적어보면,

:

\left(1071, 1029\right) = \left(1029, 42\right) = \left(42, 21\right) = \left(21, 0\right)=21

과 같이 쓸 수 있다.

a, b \in \mathbb{Z}

이고,

a\ge b

라고 하자.

그러면,

a=bq+r

을 만족하는 유일한 정수

q, r

이 존재한다. 이때,

0 \le r < b

이다.

\left(a, b\right) = d

,

a=d\alpha

,

b=d\beta

라고 하자. 즉,

\alpha

와

\beta

는 서로소이다.

:

a=bq+r.

:

\Rightarrow d\alpha =d\beta q+r.

:

\Rightarrow d|r.

(즉, r은 d의 배수)

이제,

r=d\rho.

라고 하자.

여기서 β와 ρ가 서로소라면, b(= dβ)와 r(=dρ)의 최대 공약수도 d가 된다.

만약

\left(\beta, \rho\right) = d' > 1

(서로소가 아닌 수, 즉 다른 공약수를 가지는 수)이라면,

\beta = d'\beta'

,

\rho=d'\rho'

으로 두었을 때,

:

a=bq+r.

:

\Rightarrow d\alpha = d\beta q+d\rho = d d'\beta' q + d d' \rho'= d d'\left(\beta' q + \rho'\right).

:

\Rightarrow \alpha = d'\left(\beta' q + \rho'\right).

이 되므로,

d'|\alpha

이다. (즉, α는 d'의 배수 )

즉,

d'|\alpha, d'|\beta

가 되어

\alpha

와

\beta

는 서로소라는 것에 모순이다.

이는

\left(\beta, \rho\right) = d' > 1

라는 가정에서 나타나는 모순이므로

\left(\beta, \rho\right) = 1

(즉, β와 ρ는 서로소)이다.

따라서

\left(b, r\right) = d

이다.

쉽게 풀면 다음과 같다.

A

를

B

로 나눈 몫을

Q

, 나머지를

R

이라고 할 때,

A=BQ+R

로 나타낼 수 있다.

A

와

B

의 최대 공약수를

G

라고 할 때,

R=A-BQ

이므로

R

도

G

로 나눌 수 있게 된다. 즉,

G

는

R

과

B

의 공약수가 된다. 따라서

R=GR_1

,

B=GB_1

라고 쓸 수 있다. 이때

R_1

,

B_1

은 서로소, 즉 공약수를 갖지 않는다.

R_1

,

B_1

가 공약수

C

를 가지면

R_1=CR_2

,

B_1=CB_2

가 되어,

R=GR_1=GCR_2

,

B=GB_1=GCB_2

라고 쓸 수 있다. 그러면,

A=BQ+R=GCB_2Q+GCR=GC(B_2Q+R_2 )

가 된다. 이때

A

,

B

의 최대 공약수가

CG

가 되어

G

가 최대공약수라는 것과 모순된다. 따라서

A

와

B

의 최대 공약수

G

는

R

과

B

의 최대 공약수이다.

3. 2. 다항식의 경우

다항식에도 유클리드 호제법을 적용하여 최대차수공약다항식을 구할 수 있다. 두 다항식

f, g \in \mathbb{C}[x]

(

\operatorname{deg}f\ge \operatorname{deg}g

)에 대해,

f

를

g

로 나눈 나머지를

r(x)

라 하면 (

0 \le \operatorname{deg}r < \operatorname{deg}g

) 다음이 성립한다.

:

\left(f, g\right) = \left(g, r\right).

여기서

\left(f, g\right)

는

f

와

g

의 최대차수공약다항식을 의미한다.

예를 들어

f(x)=x^3+2x^2+x, g(x)=x^2-1

인 경우,

:

x^3+2x^2+x=(x^2-1)(x+2)+(2x+2).

:

x^2-1=(2x+2)\left(\frac{x-1}{2}\right).

이므로,

\left(x^3+2x^2+x, x^2-1\right) = \left(x^2-1, 2x+2\right)=\left(2x+2, 0\right)=x+1

이다.

이는

\mathbb{C}[x]

에서 상수가 가역원이므로, 공약다항식의 계수를 조절할 수 있기 때문이다.

다항식에 대한 유클리드 호제법의 정당성은 정수의 경우와 유사하게 증명할 수 있다.^[21]

f\in\mathbb{C}[x],g \in \mathbb{C}[x]\setminus\{0\}

이고,

\operatorname{deg}f\ge \operatorname{deg}g

라고 하자.

유클리드 정역의 성질에 의해,

f=gq+r

을 만족하는 유일한 다항식

q, r

이 존재한다. (단,

r=0

이거나

\operatorname{deg}r < \operatorname{deg}g

)

\left(f, g\right) = d, f=df', g=dg'

라고 하면 (

\operatorname{deg}(f',g')=0

),

:

f=gq+r

:

\Rightarrow df' =dg'q+r

:

\Rightarrow d|r

.

r=dr'

라고 하고,

\left(g', r'\right) = d'

이 상수가 아니라고 가정하면,

g' = d'g'', r'=d'r''

으로 두었을 때,

:

f=gq+r

:

\Rightarrow df' = dg'q+dr' = d d'g'' q + d d' r''= d d'\left(g'' q + r''\right)

:

\Rightarrow f' = d'\left(g'' q + r''\right)

이 되므로,

d'|f'

이다.

즉,

d'|f', d'|g'

이 되어

\operatorname{deg}(f',g')=0

이라는 것에 모순이다.

따라서

\operatorname{deg}\left(g', r'\right) = 0

이고, 이는

\left(g, r\right) = d

임을 의미한다.

4. 확장된 유클리드 호제법

확장된 유클리드 호제법은 두 정수 ''m'', ''n''의 최대공약수(gcd(''m'',''n''))뿐만 아니라, ''mx'' + ''ny'' = gcd(''m'', ''n'')을 만족하는 정수 ''x'', ''y''를 찾는 방법이다. 이 식은 베주의 정의라고 불린다.^[19]

특히, ''m'', ''n''이 서로소인 경우(gcd(''m'',''n'') = 1), 이 알고리즘은 ''mx'' + ''ny'' = 1을 만족하는 정수해 (''x'', ''y'')를 제공하며, 여기서 ''x''는 ''m''의 모듈로 연산에서의 곱셈 역원이 된다. 즉, ''x''는 ''m''으로 나눈 나머지가 같은 수들의 집합에서 곱셈에 대한 역원 역할을 한다.

일반적으로, m = r₀, n = r₁에서 유클리드 호제법의 각 과정은 다음과 같이 반복될 수 있다.

: $r_{0} = k_{0}r_{1} + r_{2} \ \ ( 0 < r_{2} < r_{1})$

: $r_{1} = k_{1}r_{2} + r_{3} \ \ ( 0 < r_{3} < r_{2})$

: $r_{2} = k_{2}r_{3} + r_{4} \ \ ( 0 < r_{4} < r_{3})$

: $...$

: $r_{h - 1} = k_{h - 1}r_{h} + 0$

행렬을 사용하면, 다음과 같이 표현할 수 있다.

: $\begin{pmatrix}r_{0} \\r_{1} \\\end{pmatrix}=\begin{pmatrix}k_{0} & 1 \\1 & 0 \\\end{pmatrix}\begin{pmatrix}k_{1} & 1 \\1 & 0 \\\end{pmatrix}\begin{pmatrix}k_{2} & 1 \\1 & 0 \\\end{pmatrix}...\begin{pmatrix}k_{h-1} & 1 \\1 & 0 \\\end{pmatrix}\begin{pmatrix}r_{h} \\0 \\\end{pmatrix}$

$K_{i}=\begin{pmatrix}k_{i} & 1 \\1 & 0 \\\end{pmatrix}$ 라고 하면, $|K_{i}|=-1$ 이므로 역행렬 $K_{i}^{-1}$ 이 존재하고,

: $\begin{pmatrix}k_{h-1} & 1 \\1 & 0 \\\end{pmatrix}^{-1}...\begin{pmatrix}k_{2} & 1 \\1 & 0 \\\end{pmatrix}^{-1}\begin{pmatrix}k_{1} & 1 \\1 & 0 \\\end{pmatrix}^{-1}\begin{pmatrix}k_{0} & 1 \\1 & 0 \\\end{pmatrix}^{-1}\begin{pmatrix}r_{0} \\r_{1} \\\end{pmatrix}=\begin{pmatrix}r_{h} \\0 \\\end{pmatrix}$

$K_{i}^{-1}=\begin{pmatrix}0 & 1 \\1 & -k_{i} \\\end{pmatrix}$ 을 고려하면,

: $\begin{pmatrix}0 & 1 \\1 & -k_{h - 1} \\\end{pmatrix}...\begin{pmatrix}0 & 1 \\1 & -k_{2} \\\end{pmatrix}\begin{pmatrix}0 & 1 \\1 & -k_{1} \\\end{pmatrix}\begin{pmatrix}0 & 1 \\1 & -k_{0} \\\end{pmatrix}\begin{pmatrix}m \\n \\\end{pmatrix}=\begin{pmatrix}\gcd(m, n) \\0 \\\end{pmatrix}$

이 된다.

: $\begin{pmatrix}x & y \\u & v \\\end{pmatrix}=\begin{pmatrix}0 & 1 \\1 & -k_{h - 1} \\\end{pmatrix}...\begin{pmatrix}0 & 1 \\1 & -k_{2} \\\end{pmatrix}\begin{pmatrix}0 & 1 \\1 & -k_{1} \\\end{pmatrix}\begin{pmatrix}0 & 1 \\1 & -k_{0} \\\end{pmatrix}$

이라고 놓고, 유클리드 호제법의 각 과정에서 얻어진 $k_{0}$ , $k_{1}$ , $k_{2}$ 등을 사용하여 우변을 계산하면, 좌변의 $x$ , $y$ 가 구해지며, 이는 베주 항등식 ''mx'' + ''ny'' = gcd(''m'',''n'')을 만족한다.

4. 1. 정수의 경우

확장된 유클리드 호제법을 이용하면, 주어진 두 정수 ''m'', ''n''에 대해 ''am'' + ''bn'' = gcd(''m'', ''n'')을 만족하는 정수 ''a'', ''b''를 구할 수 있다. 이 식은 베주의 정의라고 불린다.^[15] 특히, ''m'', ''n''이 서로소(gcd(''m'',''n'') = 1)인 경우, 이 식은 ''am'' + ''bn'' = 1이 되고, 여기서 ''a''는 모듈로 연산의 곱의 역원이 된다.

예를 들어, 1071과 462의 최대공약수(GCD)를 구하는 과정은 다음과 같다.^[15]

1071 = 2 * 462 + 147
462 = 3 * 147 + 21
147 = 7 * 21 + 0

따라서 gcd(1071, 462) = 21이다. 이를 통해,

21 = 1029 - 24 * 42
= 1029 - 24 * (1071 - 1 * 1029)
= -24 * 1071 + 25 * 1029

이므로, ''a'' = -24, ''b'' = 25가 된다.

일반적으로, m = r₀, n = r₁에서 유클리드 호제법의 각 과정을 반복하면 다음과 같다.

r₀ = k₀r₁ + r₂ ( 0 < r₂ < r₁)
r₁ = k₁r₂ + r₃ ( 0 < r₃ < r₂)
r₂ = k₂r₃ + r₄ ( 0 < r₄ < r₃)
...
r_{h - 1} = k_{h - 1}r_h + 0

이 과정에서 행렬을 이용하여 표현하면 다음과 같다.

:

\begin{pmatrix}r_{0} \\r_{1} \\\end{pmatrix}=\begin{pmatrix}k_{0} & 1 \\1 & 0 \\\end{pmatrix}\begin{pmatrix}k_{1} & 1 \\1 & 0 \\\end{pmatrix}\begin{pmatrix}k_{2} & 1 \\1 & 0 \\\end{pmatrix}...\begin{pmatrix}k_{h-1} & 1 \\1 & 0 \\\end{pmatrix}\begin{pmatrix}r_{h} \\0 \\\end{pmatrix}

여기서 K_i = 라고 하면, |K_i| = -1 이므로 K_i^-1이 존재하고,

:

\begin{pmatrix}k_{h-1} & 1 \\1 & 0 \\\end{pmatrix}^{-1}...\begin{pmatrix}k_{2} & 1 \\1 & 0 \\\end{pmatrix}^{-1}\begin{pmatrix}k_{1} & 1 \\1 & 0 \\\end{pmatrix}^{-1}\begin{pmatrix}k_{0} & 1 \\1 & 0 \\\end{pmatrix}^{-1}\begin{pmatrix}r_{0} \\r_{1} \\\end{pmatrix}=\begin{pmatrix}r_{h} \\0 \\\end{pmatrix}

K_i^-1 = 을 고려하면,

:

\begin{pmatrix}0 & 1 \\1 & -k_{h - 1} \\\end{pmatrix}...\begin{pmatrix}0 & 1 \\1 & -k_{2} \\\end{pmatrix}\begin{pmatrix}0 & 1 \\1 & -k_{1} \\\end{pmatrix}\begin{pmatrix}0 & 1 \\1 & -k_{0} \\\end{pmatrix}\begin{pmatrix}m \\n \\\end{pmatrix}=\begin{pmatrix}\gcd(m, n) \\0 \\\end{pmatrix}

이 된다.

이라고 놓고, 유클리드 호제법의 각 과정에서 얻어진 k₀, k₁, k₂ 등을 사용하여 우변을 계산하면, 좌변의 x, y가 구해지며, 이는 베주 항등식 mx + ny = gcd(m,n)을 만족한다.

4. 2. 다항식의 경우

f, g \in \mathbb{C}[x]

의 최대차수공약다항식을

\left(f, g\right)

라고 하면,

fp + gq = \left(f, g\right)

인

p, q \in \mathbb{C}[x]

를 찾을 수 있다. 예를 들어,

f(x)=x^3+2x^2+x, g(x)=x^2-1

일 때,

:

x^3+2x^2+x=(x^2-1)(x+2)+(2x+2).

:

x^2-1=(2x+2)\left(\frac{x-1}{2}\right).

이므로

:

2x+2=x^3+2x^2+x-(x^2-1)(x+2)

이다.

특히,

\left(f, g\right)=1

인 경우

fp + gq = 1

인

p, q \in \mathbb{C}[x]

를 찾을 수 있다.

5. 응용

유클리드 호제법의 다른 버전에서는 각 단계에서 음의 나머지의 크기가 일반적인 양의 나머지보다 작을 때 몫을 1 증가시킨다.^[24]^[25] 이전에는 다음 방정식이 있었다.

: ''r''_''k''−2 = ''q''_''k'' ''r''_''k''−1 + ''r''_''k''

이는 ''r''_''k''−1 > ''r''_''k'' > 0을 가정했다. 그러나 다음과 같은 대안적인 음의 나머지 ''e''_''k''를 계산할 수 있다.

: ''r''_''k''−2 = (''q''_''k'' + 1) ''r''_''k''−1 + ''e''_''k'' (만약 ''r''_''k''−1 > 0 인 경우)

: ''r''_''k''−2 = (''q''_''k'' − 1) ''r''_''k''−1 + ''e''_''k'' (만약 ''r''_''k''−1 < 0 인 경우)

만약 ''r''_''k''가 ''e''_''k''^영어 < ''r''_''k''일 때 ''e''_''k''^영어로 대체된다면, 다음을 만족하는 유클리드 호제법의 변형을 얻게 된다.

: ''r''_''k''^영어 ≤ ''r''_''k''−1^영어 / 2

레오폴트 크로네커는 이 버전이 유클리드 호제법의 어떤 버전보다도 가장 적은 단계를 필요로 함을 보였다.^[24]^[25] 더 일반적으로, 모든 입력 숫자 ''a''와 ''b''에 대해, 단계 수가 최소가 되는 것은 $\left |\frac{r_{k+1}}{r_k}\right |<\frac{1}{\varphi}\sim 0.618,$ 을 만족하도록 ''q''_''k''^영어가 선택될 때이며, 여기서 $\varphi$ 는 황금비이다.^[26]

6. 계산 복잡도

유클리드 호제법은 매우 효율적인 알고리즘으로, 입력되는 두 수의 자릿수에 비례하는 시간 안에 최대공약수를 찾을 수 있다. 라메의 정리에 따르면, 유클리드 호제법을 이용하여 나머지를 취하는 조작을 최악의 경우라도 작은 수를 십진법으로 표시한 자리수의 5배를 반복하기 전에 최대공약수에 이른다.^[27] 일반적으로 유클리드 호제법은 소인수분해보다 훨씬 빠른 알고리즘으로 알려져 있다.

실제로, 계산 복잡성 이론에서는 최대공약수를 구하는 것은 "쉬운 문제"로 알려져 있으며, 소인수 분해는 "어려운 문제"라고 여겨진다. 입력된 두 정수 가운데 작은 정수 ''n''의 자릿수를 ''d''라고 하면, 유클리드 호제법에서는 O(''d'') 회의 나눗셈으로 최대공약수를 구할 수 있다. 자릿수 ''d''는 O(log ''n'')이므로, 유클리드 호제법에서는 O(log ''n'') 회의 나눗셈으로 최대공약수를 구할 수 있다.

7. 다른 수 체계로의 확장

유클리드 호제법은 정수뿐만 아니라 다른 수 체계에도 적용할 수 있도록 일반화되었다. 예를 들어, 유리수 `n/m`의 연분수 전개는 유클리드 호제법의 나눗셈 모양과 같다.

1071과 462의 최대공약수를 구하는 예시를 통해 이를 확인할 수 있다. 유클리드 호제법을 적용하면 다음과 같은 과정을 거친다.

단계	방정식	몫 및 나머지
0	1071 = q₀ × 462 + r₀	q₀ = 2, r₀ = 147
1	462 = q₁ × 147 + r₁	q₁ = 3, r₁ = 21
2	147 = q₂ × 21 + r₂	q₂ = 7, r₂ = 0 (알고리즘 종료)

이 과정에서 마지막 나머지가 0이므로, 알고리즘은 21을 1071과 462의 최대공약수로 반환한다.

유클리드 호제법의 뺄셈 기반 애니메이션. 1071x462 크기의 직사각형에서 시작하여, 462x462 정사각형을 배치하면 462x147 직사각형이 남는다. 이후 147x147 정사각형, 21x147 직사각형, 21x21 정사각형 순으로 덮어 나가면 빈 영역이 남지 않는다. 가장 작은 정사각형의 크기 21이 1071과 462의 최대공약수이다.

이처럼 유클리드 호제법은 타일링으로 시각화할 수 있다.^[19] a × b 직사각형을 정사각형 타일로 덮는 과정을 생각해보자. b × b 정사각형으로 시작하여, 남는 부분을 r₀ × r₀, r₁ × r₁, ... 정사각형으로 덮어 나간다. 잔여 직사각형이 없을 때, 즉 정사각형 타일이 이전 잔여 직사각형을 정확히 덮을 때 과정이 끝난다. 가장 작은 정사각형 타일의 변의 길이는 원래 직사각형의 최대공약수이다.

레오폴트 크로네커는 각 단계에서 음의 나머지의 크기가 양의 나머지보다 작으면 몫을 1 증가시키는 유클리드 호제법의 변형이 가장 적은 단계를 필요로 함을 보였다.^[24]^[25] 또한, 황금비를 이용하여 단계 수가 최소가 되는 조건을 찾을 수 있다.^[26]

8. 같이 보기

최대공약수
베주 항등식
확장된 유클리드 호제법
연분수

참조

_[1] 서적 Topics in Algebra
_[2] 간행물 Note sur la limite du nombre des divisions dans la recherche du plus grand commun diviseur entre deux nombres entiers
_[3] 간행물 Origins of the analysis of the Euclidean algorithm 1994-11-01
_[4] 서적
_[5] 서적
_[6] 서적
_[7] 서적
_[8] 서적 Discrete Mathematics Macmillan
_[9] 서적
_[10] 서적
_[11] 서적 Excursions in number theory Oxford University Press
_[12] 서적
_[13] 서적
_[14] 서적
_[15] 서적
_[16] 서적
_[17] 서적
_[18] 서적 Discrete Mathematics: Elementary and Beyond Springer-Verlag
_[19] 간행물 A Visual Euclidean Algorithm
_[20] 서적 Abstract Algebra John Wiley & Sons, Inc.
_[21] 서적
_[22] 서적
_[23] 서적
_[24] 서적
_[25] 서적 Theory of Numbers Macmillan
_[26] 간행물 Le meilleur algorithme d'Euclide pour ''K''[''X''] et '''Z'''
_[27] 서적
_[28] 서적 Number Theory Birkhäuser
_[29] 서적 Companion encyclopedia of the history and philosophy of the mathematical sciences Routledge
_[30] 서적 Science Awakening https://archive.org/[...] P. Noordhoff Ltd
_[31] 간행물 The Discovery of Incommensurability by Hippasus of Metapontum
_[32] 서적 Mathematics in Aristotle https://archive.org/[...] Oxford Press
_[33] 서적 The Mathematics of Plato's Academy: A New Reconstruction Oxford University Press
_[34] 간행물 Eudoxus-Studien I. Eine voreuklidische Proportionslehre und ihre Spuren bei Aristoteles und Euklid
_[35] 서적 History of continued fractions and Padé approximants Springer-Verlag, Berlin
_[36] 간행물
_[37] 간행물
_[38] 간행물
_[39] 간행물
_[40] 간행물
_[41] 서적 The Elements of Algebra in Ten Books http://www.e-rara.ch[...] University of Cambridge Press 2016-11-01
_[42] 간행물
_[43] 간행물
_[44] 간행물
_[45] 간행물
_[46] 간행물
_[47] 논문 Mémoire sur la résolution des équations numériques
_[48] 논문 Generalization of the Euclidean algorithm for real numbers to all dimensions higher than two
_[49] 논문 Jazzing Up Euclid's Algorithm http://www.sciencene[...] 2002-08-12
_[50] 논문 The Best of the 20th Century: Editors Name Top 10 Algorithms https://www.siam.org[...] Society for Industrial and Applied Mathematics 2016-07-19
_[51] 논문 A game based on the Euclidean algorithm and a winning strategy for it
_[52] 논문 Properties of a game based on Euclid's algorithm
_[53] 간행물
_[54] 서적 Elementary Number Theory: A Problem Oriented Approach https://archive.org/[...] MIT Press
_[55] 서적 Elementary Number Theory Springer-Verlag
_[56] 간행물
_[57] 간행물
_[58] 간행물
_[59] 간행물
_[60] 간행물
_[61] 간행물
_[62] 서적 Elementary Number Theory with Applications Harcourt/Academic Press
_[63] 서적 Algorithmic number theory MIT Press
_[64] 간행물
_[65] 간행물
_[66] 간행물
_[67] 간행물
_[68] 간행물
_[69] 간행물
_[70] 간행물
_[71] 간행물
_[72] 간행물
_[73] 간행물
_[74] 간행물
_[75] 서적 Error Correction Coding: Mathematical Methods and Algorithms John Wiley and Sons
_[76] 간행물
_[77] 간행물
_[78] 서적 Concrete mathematics Addison-Wesley
_[79] 서적 Elements of Number Theory https://archive.org/[...] Dover
_[80] 간행물
_[81] 간행물
_[82] 논문 Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer
_[83] 논문 Asymptotically fast factorization of integers
_[84] 논문 Factoring integers with elliptic curves
_[85] 간행물
_[86] 간행물
_[87] 서적 Traité d'arithmétique à l'usage des élèves qui se destinent à l'École Polytechnique https://archive.org/[...] Courcier
_[88] 서적 Traité élémentaire d'arithmétique à l'usage des candidats aux écoles spéciales Derivaux
_[89] 논문 Note sur la limite du nombre des divisions dans la recherche du plus grand commun diviseur entre deux nombres entiers
_[90] 논문 On the Number of Divisions in Finding a G.C.D
_[91] 서적 Mathematical Gems II The [[Mathematical Association of America]]
_[92] 간행물
_[93] 간행물
_[94] 간행물
_[95] 간행물
_[96] 간행물
_[97] 간행물
_[98] 간행물
_[99] 간행물
_[100] 논문 On the average length of finite continued fractions
_[101] 논문 Evaluation of Porter's constant
_[102] 논문 On a Theorem of Heilbronn
_[103] 논문 Evaluation of Porter's Constant
_[104] 논문 The Number of Steps in the Euclidean Algorithm
_[105] 서적 Number Theory and Analysis Plenum
_[106] 서적
_[107] 논문 On the Asymptotic Analysis of the Euclidean Algorithm
_[108] 서적
_[109] 서적
_[110] 서적
_[111] 서적
_[112] 서적 Mathematica in Action Springer-Verlag
_[113] 서적
_[114] 서적
_[115] 서적 High primes and misdemeanours: lectures in honour of the 60th birthday of Hugh Cowie Williams https://books.google[...] American Mathematical Society
_[116] 서적
_[117] 논문 Computational problems associated with Racah algebra
_[118] 서적
_[119] 서적
_[120] 논문 Euclid's Algorithm for Large Numbers
_[121] 논문 Two fast GCD algorithms
_[122] 논문 The accelerated GCD algorithm
_[123] 서적 The Design and Analysis of Computer Algorithms https://archive.org/[...] Addison–Wesley
_[124] 논문 Schnelle Berechnung von Kettenbruchentwicklungen
_[125] 서적 Algorithmic Number Theory: Proc. ANTS-III, Portland, OR Springer-Verlag
_[126] 서적 Proceedings of the 17th IEEE Symposium on Computer Arithmetic (ARITH-17) IEEE Computer Society Press
_[127] 논문 On Schönhage's algorithm and subquadratic integer gcd computation http://www.lysator.l[...]
_[128] 서적 A History of Mathematics https://archive.org/[...] Wiley
_[129] 서적 A History of Mathematics https://archive.org/[...] Macmillan
_[130] 서적 Algorithmic Cryptanalysis https://books.google[...] CRC Press
_[131] 서적 Mathematical Omnibus: Thirty Lectures on Classic Mathematics https://books.google[...] American Mathematical Society
_[132] 서적 The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes https://books.google[...] John Wiley & Sons
_[133] 서적 Explorations in Quantum Computing https://books.google[...] Springer
_[134] 서적 Algebra Addison–Wesley
_[135] 서적
_[136] 서적
_[137] 서적 Convolutions in French Mathematics, 1800-1840: From the Calculus and Mechanics to Mathematical Analysis and Mathematical Physics. Volume II: The Turns https://books.google[...] Birkhäuser
_[138] 서적 Solving Ordinary Differential Equations I: Nonstiff Problems https://books.google[...] Springer
_[139] 문서
_[140] 논문 Theoria residuorum biquadraticorum
_[141] 서적
_[142] 서적 Continued Fractions https://books.google[...] World Scientific
_[143] 서적 Theory of Algebraic Integers https://books.google[...] Cambridge University Press
_[144] 서적 Numbers and Symmetry: An Introduction to Algebra https://books.google[...] CRC Press
_[145] 서적 Introduction to Number Theory https://archive.org/[...] Prentice-Hall
_[146] 서적
_[147] 서적
_[148] 서적 Concrete Abstract Algebra: From Numbers to Gröbner Bases https://books.google[...] Cambridge University Press
_[149] 서적
_[150] 서적
_[151] 서적 Rings and Factorization https://archive.org/[...] Cambridge University Press
_[152] 서적
_[153] 서적
_[154] 간행물 Mémoire sur la résolution, en nombres complexes, de l'équation Aⁿ + Bⁿ + Cⁿ = 0
_[155] 서적 Fermat's last theorem: a genetic introduction to algebraic number theory Springer
_[156] 서적
_[157] 서적 Topics in Number Theory, Volumes I and II https://archive.org/[...] Dover Publications
_[158] 간행물 A quadratic field which is Euclidean but not norm-Euclidean
_[159] 간행물 On Euclidean rings of algebraic integers
_[160] 서적
_[161] 서적
_[162] 서적 Elementary Number Theory, Group Theory and Ramanujan Graphs Cambridge University Press
_[163] 서적 Classical Theory of Algebraic Numbers https://books.google[...] Springer-Verlag

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com