주기배가 분기

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 예시
3. 1차원 사상에서의 주기 배가 분기
4. 실험적 관찰
참조

1. 개요

주기 배가 분기는 동적 시스템에서 주기가 두 배로 증가하는 분기 유형을 의미한다. 로지스틱 맵, 쿠라모토-시바신스키 방정식, 수정된 필립스 곡선 등 다양한 시스템에서 나타나며, 혼돈으로의 전이 과정에서 중요한 역할을 한다. 실험적으로 대류 롤, 전자 회로 등에서 관찰되었으며, 1차원 사상과 같은 수학적 모델을 통해 이해할 수 있다.

더 읽어볼만한 페이지

분기 이론 - 분기 다이어그램
분기 다이어그램은 동역학계에서 분기 매개변수의 변화에 따라 시스템의 고정점, 주기 궤도, 카오스적 끌개가 어떻게 변하는지 보여주는 도표로, 시스템의 안정성을 분석하고 예측하는 데 응용된다.
분기 이론 - 분기 (동역학계)
분기는 동역학계에서 매개변수 변화에 따라 평형점, 주기 궤도 등의 질적 변화가 발생하는 현상이며, 국소적 분기와 대역적 분기로 나뉜다.

주기배가 분기
주기 배가 분기
개요
분야	역학계
관련 개념	분기 이론, 혼돈 이론, 페이겐바움 상수
상세 정보
설명	역학계에서 매개변수의 변화에 따라 주기적인 해의 주기가 두 배로 증가하는 현상
발생 조건	비선형 시스템에서 특정 매개변수 값에 도달할 때 발생
특징	초기에는 안정적인 주기를 가지는 시스템이 매개변수 변화에 따라 불안정해지면서 주기가 두 배로 늘어남. 이러한 주기 배가 과정이 반복되면서 시스템은 결국 혼돈 상태로 진입할 수 있음.
예시	로지스틱 사상 만델브로 집합
추가 정보
페이겐바움 상수와의 관계	주기 배가 분기가 일어나는 매개변수 값들의 간격은 페이겐바움 상수에 따라 기하급수적으로 감소함.
관련 링크
참고 자료	Period-doubling bifurcation - Wikipedia (영어) 周期倍分岐 - 维基百科，自由的百科全书 (중국어)

2. 예시

주기배가 분기의 예시로는 다음이 있다.

실수 $x$ 와 실수 파라미터 $\mu$ 를 사용한 1차원 사상

:

x \to f(x,\mu) = - x - \mu x + x^3

:

x = 0

은

\mu < 0

에서 안정적인 고정점(

f(x,\mu) = x

를 만족하는 1주기점)이지만,

\mu > 0

에서는 불안정하다.

\mu > 0

에서는

x = \pm \sqrt{\mu}

는 2주기점이 되고 안정적이다. 따라서

\mu

가 음수에서 양수로 증가하는 과정에서 0을 지나는 순간, 안정적인 고정점(1주기점)이 불안정해지고, 그 대신 안정적인 2주기점이 양쪽에 생겨난다.

로지스틱 맵
만델브로 집합의 실수 단면과 관련된 복소 이차 맵
쿠라모토-시바신스키 방정식
수정된 필립스 곡선

2. 1. 로지스틱 맵

로지스틱 맵은 다음과 같다.

:

x_{n+1} = r x_n (1 - x_n)

여기서

x_n

는 (이산) 시간

n = 0, 1, 2, \ldots

의 함수이다.^[3] 파라미터

r

은 구간

[0,4]

에 속하는 것으로 가정하며, 이 경우

x_n

는

[0,1]

에서 경계가 정해진다.

r

이 1과 3 사이일 때,

x_n

는 안정적인 고정점

x_* = (r-1)/r

로 수렴한다.

r

이 3과 3.44949 사이일 때,

x_n

은

r

에 따라 달라지는 두 값

x_*

와

x'_*

사이에서 영구적인 진동으로 수렴한다.

r

이 커질수록 4개의 값, 8개, 16개, 32개 등으로 진동이 나타난다. 이러한 주기 배가는

r \approx 3.56995

에서 절정에 달하며, 그 이후에는 더 복잡한 영역이 나타난다.

r

이 증가함에 따라,

r=3.83

근처와 같이 대부분의 시작 값이 하나 또는 소수의 안정적인 진동으로 수렴하는 몇 개의 간격이 있다.

어떤 양의 정수

n

에 대해 주기가

2^n

인 간격에서, 모든 점이 실제로 주기

2^n

을 갖는 것은 아니다. 이것들은 간격이 아닌 단일 점이다. 이러한 점들은 불안정한 궤도에 있다고 하며, 그 이유는 근처의 점들이 그들과 같은 궤도에 접근하지 않기 때문이다.

2. 2. 이차 맵

만델브로 집합의 실수 단면과 관련된 복소 이차 맵은 주기배가 분기를 시각적으로 보여주는 예시이다.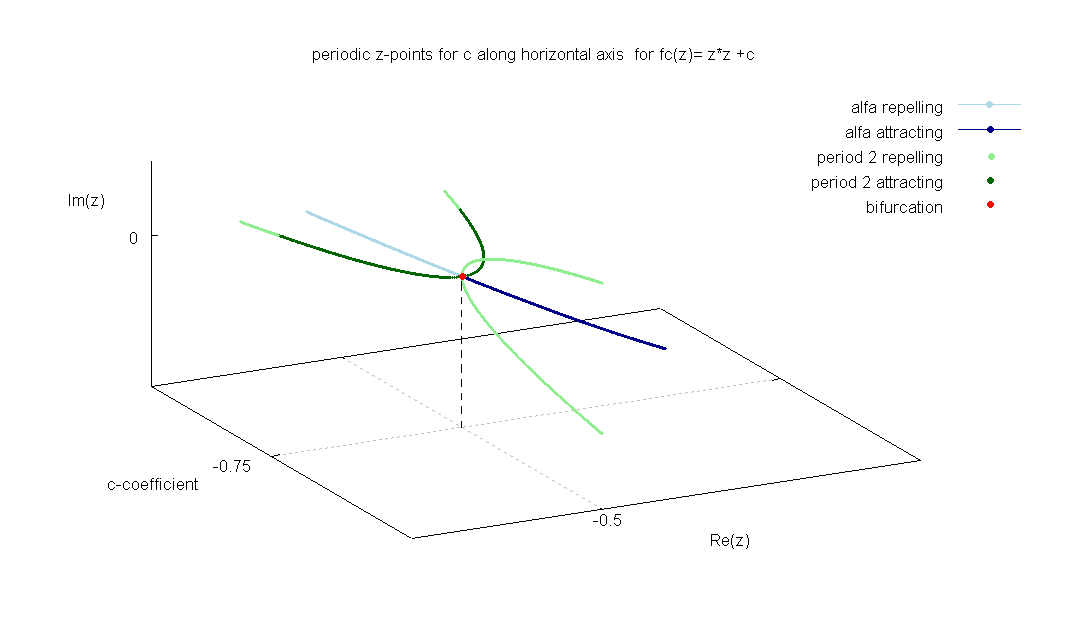

2. 3. 쿠라모토-시바신스키 방정식

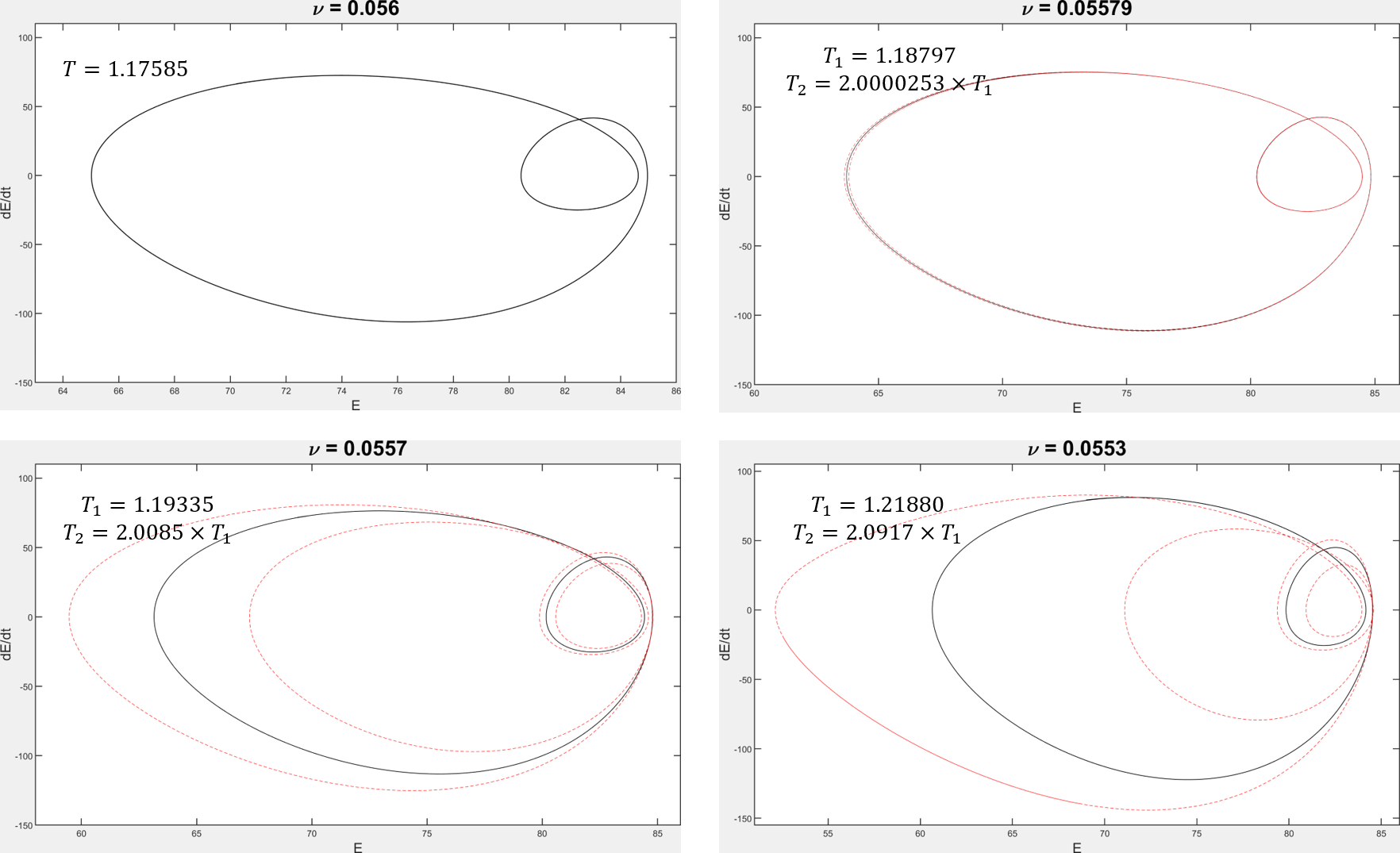
쿠라모토-시바신스키 방정식은 주기 배가 분기를 나타내는 시공간적으로 연속적인 동적 시스템의 한 예이다. 이는 원래 화염 전파 모델로 도입된 가장 잘 연구된 비선형 편미분 방정식 중 하나이다.^[4]

1차원 쿠라모토-시바신스키 방정식은 다음과 같다.

:

u_t + u u_x + u_{xx} + \nu \, u_{xxxx} = 0

경계 조건에 대한 일반적인 선택은 공간적 주기성이다:

u(x + 2 \pi, t) = u(x,t)

.

\nu

의 큰 값의 경우

u(x,t)

는 정상(시간 독립) 해 또는 단순한 주기 궤도로 진화한다.

\nu

가 감소함에 따라 동역학은 결국 혼돈을 일으킨다. 질서에서 혼돈으로의 전이는 주기 배가 분기의 계단을 통해 발생하며,^[5]^[6] 그중 하나가 그림에 나와 있다.

2. 4. 수정된 필립스 곡선

필립스 곡선은 실업률과 인플레이션 간의 관계를 나타내는 곡선으로, 수정된 필립스 곡선 모델에서도 주기 배가 분기가 나타날 수 있다. 다음은 수정된 필립스 곡선에 대한 로지스틱 맵을 나타낸 것이다.

:

\pi_{t} = f(u_{t}) + b \pi_{t}^e

:

\pi_{t+1} = \pi_{t}^e + c (\pi_{t} - \pi_{t}^e)

:

f(u) = \beta_{1} + \beta_{2} e^{-u} \,

:

b > 0, 0 \leq c \leq 1, \frac {df} {du} < 0

여기서:

$\pi$ 는 실제 인플레이션을 나타낸다.
$\pi^e$ 는 예상 인플레이션을 나타낸다.
u는 실업률을 나타낸다.
$m - \pi$ 는 통화 공급 증가율을 나타낸다.

\beta_{1} = -2.5, \ \beta_{2} = 20, \ c = 0.75

를 유지하고

b

를 변경하면, 시스템은 주기 배가 분기를 거쳐 결국 카오스가 된다.

3. 1차원 사상에서의 주기 배가 분기

실수 파라미터 $\mu$ 를 사용하는 1차원 사상

: $x \to f(x,\mu) = - x - \mu x + x^3$

을 생각하자.

$x = 0$ 은 $\mu < 0$ 에서 안정적인 고정점( $f(x,\mu) = x$ 를 만족하는 1주기점)이다. 그러나 $\mu > 0$ 에서는 불안정하며, 또한 $\mu > 0$ 에서

: $f(\sqrt{\mu},\mu) = - \sqrt{\mu}$

: $f(- \sqrt{\mu},\mu) = \sqrt{\mu}$

이므로, $x = \pm \sqrt{\mu}$ 는 2주기점이 되고 안정적이다.

따라서 $\mu$ 가 음수에서 양수로 증가하는 과정에서 0을 지나는 순간, 안정적인 고정점(1주기점)이 불안정해지고, 그 대신 안정적인 2주기점이 양쪽에 생겨난다.

이로부터 위의 1차원 사상은 $\mu = 0$ 을 경계로 주기배가 분기를 일으켰다고 말한다.

4. 실험적 관찰

주기 배가는 여러 실험 시스템에서 관찰되었다.^[7] 주기 배가 연쇄에 대한 실험적 증거도 있다. 예를 들어, 물과 수은에서 대류 롤의 역학에서 4번의 주기 배가가 관찰되었다.^[8]^[9] 마찬가지로, 특정 비선형 전자 회로에서 4-5번의 배가가 관찰되었다.^[10]^[11]^[12] 그러나 연쇄에서 ''i''번째 배가 사건을 감지하는 데 필요한 실험적 정밀도는 ''i''에 따라 지수적으로 증가하여 연쇄에서 5번 이상의 배가 사건을 관찰하기 어렵게 만든다.^[13]

참조

_[1] 문서 Alligood (1996) et al., p. 532
_[2] 서적 Modern Classical Physics: Optics, Fluids, Plasmas, Elasticity, Relativity, and Statistical Physics Princeton University Press
_[3] 문서 Strogatz (2015), pp. 360–373
_[4] 간행물 An in-depth numerical study of the two-dimensional Kuramoto–Sivashinsky equation
_[5] 간행물 Predicting chaos for infinite dimensional dynamical systems: the Kuramoto-Sivashinsky equation, a case study.
_[6] 간행물 The route to chaos for the Kuramoto-Sivashinsky equation
_[7] 문서 see Strogatz (2015) for a review
_[8] 간행물 Transition to Chaotic Behavior via a Reproducible Sequence of Period-Doubling Bifurcations
_[9] 간행물 Period doubling cascade in mercury, a quantitative measurement https://hal.archives[...]
_[10] 간행물 Period Doubling and Chaotic Behavior in a Driven Anharmonic Oscillator
_[11] 간행물 Evidence for Universal Chaotic Behavior of a Driven Nonlinear Oscillator http://www.escholars[...]
_[12] 간행물 Hopping Mechanism Generating1fNoise in Nonlinear Systems
_[13] 문서 Strogatz (2015), pp. 360–373

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com