중력이상

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

중력이상은 지구 중력의 실측값과 표준 중력값의 차이를 의미하며, 지구 내부의 밀도 분포를 파악하는 데 활용된다. 표준 중력은 지구의 회전과 형태를 고려하여 계산되며, 중력 보정을 통해 지형, 고도, 조석력 등의 영향을 제거한다. 중력 보정에는 프리에어 보정, 부게 보정, 지형 보정 등이 있으며, 보정 과정을 거쳐 계산된 중력 이상은 지각의 구조와 밀도 변화를 나타낸다. 중력이상은 지구물리학 연구, 자원 탐사, 지하 구조 파악, 우주물리학 연구 등 다양한 분야에서 활용되며, 인공위성을 이용한 중력 측정 기술을 통해 지구 중력장을 정밀하게 연구할 수 있다.

더 읽어볼만한 페이지

광상학 - 광맥
광맥은 암석 내 균열에서 유체의 흐름을 보여주는 구조로, 균열 내 광물 침전으로 형성되며 지질학적 정보와 광물 자원 탐사에 중요한 역할을 한다.
광상학 - 백금족 원소
백금족 원소는 회백색 광택, 화학적 안정성, 높은 녹는점, 큰 비중, 뛰어난 전연성, 부식 저항성을 지닌 루테늄, 로듐, 팔라듐, 오스뮴, 이리듐, 백금 6가지 금속 원소의 귀금속으로, 촉매 특성이 뛰어나 자동차 배기가스 정화 촉매 등 다양한 산업 분야에 활용된다.
측지학 - 위도
위도는 지구 표면의 남북 위치를 각도로 나타내며, 지구를 회전 타원체로 가정했을 때 법선과 적도면이 이루는 각으로 측정하여 적도를 0°로 북극과 남극까지 나타내고, 기후와 지리적 특징 등에 영향을 미치는 다양한 종류가 존재한다.
측지학 - 측지계
측지계는 지구의 형태와 위치를 수학적으로 모델링하여 위도, 경도, 고도 등을 정의하고 측량, 지도 제작, GPS 등에 활용되는 기준 좌표계이다.
중력 - 중력 가속도
중력 가속도는 물체가 중력에 의해 가속되는 정도를 나타내는 값으로, 자유 낙하하는 물체의 가속도와 같으며, 지구의 경우 자전에 의한 원심력으로 인해 적도에서 가장 작고 극에서 가장 크게 나타난다.
중력 - 만유인력의 법칙
만유인력의 법칙은 모든 질량을 가진 물체들이 서로를 끌어당기는 힘에 대한 법칙으로, 뉴턴은 질량에 비례하고 거리의 제곱에 반비례한다는 것을 제시했으며, 케플러의 행성 운동 법칙을 설명하고 뉴턴 역학의 기초가 되었으나, 일반 상대성 이론이 등장하면서 저중력 한계로 여겨진다.

중력이상
개요
정의	이상 중력은 위치에서의 이상적인 중력 가속도와 관측된 중력 가속도의 차이이다.
설명	이상 중력은 특정 위치에서 예측되거나 이론적인 중력 가속도 값과 실제 측정된 중력 가속도 값 사이의 차이를 나타낸다. 이러한 차이는 해당 지역의 지하 질량 분포의 변화, 지형적 특징, 또는 지구 내부의 밀도 변화와 같은 다양한 요인에 기인할 수 있다. 이상 중력은 지질학적 구조, 광물 매장지, 지하수 분포 등을 연구하는 데 중요한 정보를 제공한다.
활용 분야	지질 구조 연구 광물 탐사 지하 자원 평가 지구 물리학 연구
계산 방법
이상 중력 계산	이상 중력 = 측정된 중력 가속도 - 이론적 중력 가속도
측정된 중력 가속도	중력계를 사용하여 특정 위치에서 직접 측정한다.
이론적 중력 가속도	지구의 회전, 모양(지오이드), 그리고 표준 밀도 모델을 기반으로 계산된다. 다양한 보정(예: 자유 공기 보정, 부게 보정, 지형 보정)을 적용하여 정확도를 높일 수 있다.
요인
지하 질량 분포	지하의 암석 밀도 변화, 광맥, 공동 등이 중력 이상을 유발할 수 있다. 밀도가 높은 물질은 중력을 증가시키고, 밀도가 낮은 물질은 중력을 감소시킨다.
지형적 특징	산, 계곡, 언덕 등의 지형은 주변 지역의 중력에 영향을 미친다. 지형 보정을 통해 이러한 영향을 제거할 수 있다.
지구 내부의 밀도 변화	맨틀 대류, 지각 구조 변화 등 지구 내부의 역학적 과정도 중력 이상을 일으킬 수 있다.
보정
자유 공기 보정 (Free-air correction)	측정 지점의 고도 변화에 따른 중력 변화를 보정한다. 고도가 높아질수록 중력은 감소하므로, 이를 보정하여 해수면 기준으로 환산한다.
부게 보정 (Bouguer correction)	측정 지점과 기준면(보통 해수면) 사이의 암석층에 의한 중력 효과를 보정한다. 이 보정은 지표면 아래에 가정한 평판(Bouguer plate)의 중력 효과를 제거한다.
지형 보정 (Terrain correction)	측정 지점 주변의 지형 기복에 의한 중력 효과를 보정한다. 산이나 계곡과 같은 지형은 중력 측정값에 영향을 미치므로, 이를 보정하여 평탄한 지형에서의 값으로 환산한다.
활용
석유 및 가스 탐사	퇴적 분지의 구조와 매장된 탄화수소 자원을 파악하는 데 사용된다.
광물 탐사	밀도가 높은 광맥이나 광상 위치를 찾는 데 활용된다.
지하수 탐사	지하수 흐름과 저장 위치를 파악하는 데 도움을 준다.
지진 연구	지각 구조와 단층을 분석하여 지진 발생 메커니즘을 연구하는 데 기여한다.
다른 행성에서의 중력 이상
달	달의 매스콘(mascons)은 달 표면 아래의 밀도 변화로 인해 발생하는 중력 이상이다. 이러한 매스콘은 초기 충돌 사건으로 인해 형성된 것으로 추정된다.
화성	화성에서도 지각 두께 변화와 지하 밀도 차이로 인한 중력 이상이 관측된다. 특히, 화성 북반구의 낮은 지대와 남반구의 높은 지대 사이의 밀도 차이가 큰 영향을 미친다.

2. 표준 중력

표준 중력은 지구 타원체 모델을 기반으로 위도에 따라 계산되는 이론적인 중력 값이다. 지구의 경우, 기준 타원체는 국제 기준 타원체이며, 타원체상의 점에 대해 예측된 중력 값은 '정상 중력'(g_n)이다.

정상 중력은 지구 전체의 중력 질량을 이상적인 모양과 자전을 고려하여 보정한 값으로, 0.1 mgal의 정확도를 가지는 공식은 다음과 같다. 더 높은 정밀도가 필요할 경우, 더 복잡한 공식으로 0.0001 mgal의 정확도로 정상 중력을 계산할 수 있다.

: $g_n = g_e(1 + \beta_1 \sin^2\lambda + \beta_2 \sin^2 2\lambda)$

:여기서 $g_e$ = 9.780327 m·s^-2, $\beta_1$ = 5.30244×10^-3, $\beta_2$ = −5.8×10^-6이다.

1672년 프랑스 천문학자 장 리셰는 카이엔 섬에 관측소를 세우면서 중력이상을 처음 발견했다. 아이작 뉴턴은 만유인력 이론을 사용하여 이 현상을 설명했는데, 측정된 중력 값이 지구의 자전에 의해 영향을 받으며, 적도에 더 가까운 카이엔은 지구 중심에서 더 멀리 떨어져 있어 중력 값이 감소한다고 보았다.

측지학과 지구물리학에서 중력이상(重力異常)은 중력의 실측값과 표준 중력의 차이를 말한다. 표준 중력은 지구 타원체 상에서의 이론적인 중력값이며, 중력이상을 측정할 때는 측정점에 대한 지형과 고도에 의한 영향을 보정해야 한다.

2. 1. 국제표준중력식

국제측지학회에서 1967년에 채택한 위도에 따른 평균 중력 값으로, 회전하는 타원체라는 지구의 특성을 고려하여 만든 식이다.^[10]

:

g_t=g_e(1+0.005278895\sin ^2 \varphi +0.000023462\sin ^4 \varphi)

적도(

\varphi=0^\circ

)에서는 약 978031.5mGal이며, 극(

\varphi=90^\circ

)에서는 983217.7mGal이다.^[10]

중력가속도 단위(mGal)는 다음과 같이 정의된다.

:

1mGal=10^{-3}Gal=10^{-3}cm/s^2=10^{-5}m/s^2

중력은 적도에서 극지방까지 약 5000mGal 정도의 변화를 보인다.^[10]

3. 중력 보정

지구 표면 특정 지점의 중력은 관측 지점의 위도, 고도, 주변 지형 등 여러 요인의 영향을 받는다. 이러한 영향들을 보정하여 실제 중력이상 값을 정확하게 구하는 과정을 중력 보정이라고 한다.

중력이상은 1672년 프랑스 천문학자 장 리셰가 카이엔 섬에서 관측소를 운영하면서 처음 발견되었다. 리셰는 파리에서 정밀하게 보정된 진자 시계가 카이엔에서는 느려지는 현상을 발견했는데, 이는 아이작 뉴턴의 만유인력 이론으로 설명되었다. 지구 자전으로 인해 적도가 극보다 부풀어 올라 카이엔이 파리보다 지구 중심에서 멀어졌고, 이로 인해 중력 값이 감소했기 때문이다.

측정된 중력 값에는 여러 요인이 영향을 미치므로, 정확한 중력이상 값을 얻기 위해서는 다음과 같은 보정 과정들이 필요하다.^[3]

'''조석 보정 (Tidal correction, △''g''_tid)''': 태양과 달은 시간에 따라 변하는 조석력을 발생시켜 중력 측정값에 약 0.3mGal의 영향을 미친다. 이 영향은 천체 물리학적 데이터와 공식을 통해 정확하게 계산하여 보정할 수 있다.
'''지형 보정 (Terrain correction, △''g''_T)''': 측정 지점 주변의 언덕이나 계곡 같은 지형은 중력 측정값에 영향을 준다. 높은 지형과 낮은 계곡 모두 중력을 감소시킨다. 지형 보정은 주변 지형 정보와 암석 밀도를 바탕으로 계산된다.
'''프리에어 보정 (Free-air correction, FAC)''': 측정 지점의 고도에 따라 중력이 변화하는 것을 보정한다. 고도가 높아질수록 지구 중심에서 멀어져 중력이 감소한다.
'''부게 보정 (Bouguer correction, BC)''': 측정 지점과 해수면 사이의 물질(주로 암석)이 중력에 미치는 영향을 보정한다.

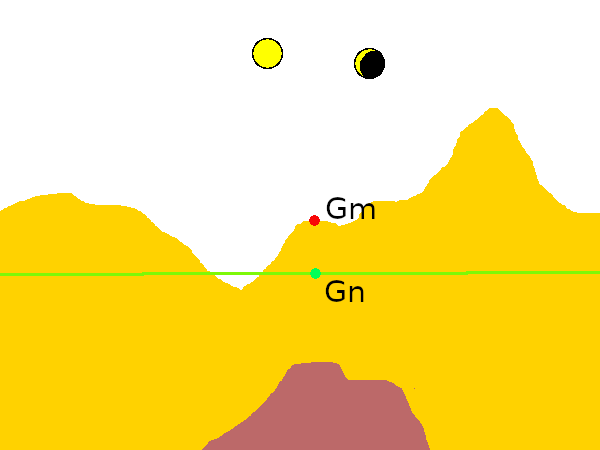
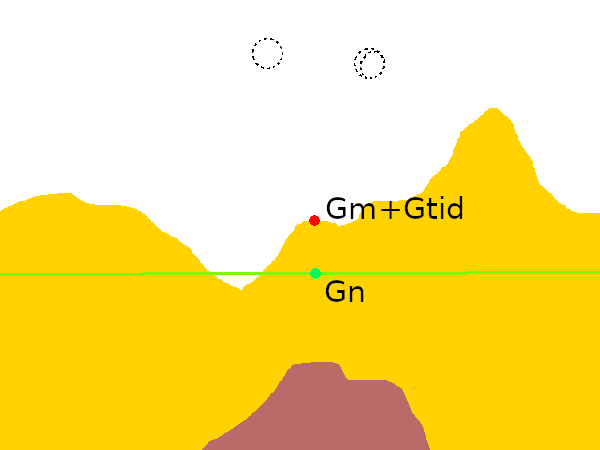
가상의 중력 측정. 중력 값은 $g_m$ 으로 표시된 빨간색 지점에서 측정됩니다. 녹색 점은 기준 타원체에 있는 정상 중력 $g_n$ 입니다.

이러한 보정을 통해 지하의 밀도 분포에 따른 중력이상 값을 얻을 수 있다.

3. 1. 프리에어 보정 (Free-air correction)

'''프리에어 보정'''은 측정 지점의 고도에 따른 중력 변화를 보정하는 과정이다. 지표면 근처에서 고도가 높아질수록 지구 중심으로부터 거리가 멀어져 중력이 감소하는 현상을 고려한다.^[11]

지구 중심으로부터 거리 증가에 따른 중력 변화는 다음과 같이 나타낼 수 있다.

:

{dg \over dR} = {d \over dR}{GM \over R^2}=-{2GM \over R^3}=-{2g \over R}

여기서 g의 평균값은 980,626 mGal, R은 6.367*10⁶m이다. 이를 통해 고도에 따른 중력 변화율을 계산하면 다음과 같다.

:

{dg \over dR}=-0.308mGal/m

즉, 지표면에서 3m 높아질 때마다 중력 가속도는 약 1Gal씩 감소한다. 따라서 해발 고도가 높은 지점은 낮은 지점보다 작은 중력 값을 갖게 된다.^[11]

서로 다른 고도에서 측정된 중력값을 비교하기 위해서는 측정값에 프리에어 보정값(FAC)을 더해야 한다. FAC는 다음과 같이 계산된다.

:

FAC=h*0.308mGal/m

(여기서 h는 해수면으로부터 측정 지점까지의 고도)

프리에어 중력이상은 관측 지점의 고도에 대한 보정이 이루어진 관측값으로, 다음과 같이 표현된다.

:

\Delta g_{fa}=g-g_t

+

FAC

여기서

g-g_t

는 회전과 적도 부근 팽창에 따른 위도 효과 보정값이고, +FAC는 고도에 의한 중력 손실 보정값이다.

프리에어 중력이상은 질량 초과 지역에서는 상대적으로 높은 값을, 질량 부족 지역에서는 상대적으로 낮은 값을 보인다. 이를 도표로 나타내면 지형과 유사한 중력 변화 양상을 확인할 수 있다.^[11]

프리에어 보정은 측정 지점의 고도 영향을 보정하여 지오이드에서의 값으로 만든 다음, 기준 중력을 뺀 값으로, 지구 내부의 밀도 불균일에 의한 중력 값의 변동을 나타낸다.

3. 2. 부게 보정 (Bouguer correction)

부게 보정은 측정 지점과 해수면 사이 물질(주로 암석)의 인력 효과를 보정하는 과정이다. 육지와 바다에서 서로 다른 방식으로 보정한다.^[12]

관측 지점 고도와 같은 두께의 무한 평판을 가정할 때, 이 평판에 의한 인력 효과(BC)는 다음과 같다.

:$BC = 2\pi \rho Gh = 0.0419 \rho h$^[12]

여기서 $ \rho $는 밀도, $G$는 만유인력 상수, $h$는 관측 지점 고도이다.

육지와 바다에서의 부게 보정은 하위 섹션을 참고한다.

3. 2. 1. 육지에서의 부게 보정

측정 지점 아래에 평균 밀도의 무한 평판을 가정하여 중력 효과를 계산하고, 이를 프리에어 이상에서 빼서 부게 이상을 구한다. 육지에서의 부게 중력이상은 프리에어 이상에서 무한판의 효과(BC)를 빼서 단순 부게 이상을 먼저 구한다.^[12]

:

\Delta g_B=\Delta g_{fa}-BC

여기서 환산밀도는 화강암의 전형적인 밀도인 2.67g/cm³을 사용한다. 그러므로,

:

BC=0.0419*2.67g/cm^3*h=0.112mGal/m*h

이다.^[12]

고도가 9m 높아질 때마다 측정 중력값에 1mGal 정도 증가하므로 최종적으로

:

\Delta g_B=\Delta g_{fa}-0.112mGal/m*h

이 된다.^[12]

위 식을 통해 중력이상에 대한 일반적인 성질을 이끌어낼 수 있다. 해수면보다 높은 관측점에서 부게 중력이상은 언제나 프리에어 중력이상보다 작다. 이는 해수면 윗부분에 의한 인력이 제거되기 때문이다. 부게 중력이상은 프리에어 중력이상에 비해 완만한 곡선 형태를 보인다. 또한, 질량 초과는 중력이상에 양의 변화, 질량 부족은 음의 변화를 일으킨다.

3. 2. 2. 바다에서의 부게 보정

해수면을 기준으로 수심과 같은 두께를 가지는, 화강암과 바닷물 밀도 차이에 해당하는 무한 평판을 가정하여 부게 보정을 실시한다. 이때 밀도는 $\rho_w=1.03g/cm^3$, $\rho_c=2.67g/cm^3$으로 가정한다.

부게 보정값($BC_s$)은 다음과 같이 주어진다.

:$BC_s=0.0419\rho h=0.0419(\rho _w- \rho _c)*h_w = -0.0687mGal/m*h_w$

즉, 수심이 14.5m 깊어질 때마다 측정 중력값은 약 1mGal 정도 감소한다. 따라서 최종적인 부게 이상($\Delta g_B$)은 프리에어 이상($\Delta g_{fa}$)에 보정값을 더하여 구한다.

:$\Delta g_B=\Delta g_{fa}+0.0687mGal/m*h_w$^[12]

3. 3. 지형 보정 (Terrain correction)

지표면의 국지적인 지형은 중력 측정에 영향을 미친다. 측정 지점보다 높은 지형과 측정 지점보다 낮은 계곡은 모두 측정된 중력 값을 감소시킨다. 이는 지형 보정 △''g''_T에 의해 고려된다. 지형 보정은 국지적인 지형에 대한 지식과 높은 지반을 구성하는 암석의 밀도 추정치로부터 계산된다. 사실상, 지형 보정은 측정 지점 주변의 지형을 평탄하게 만든다.^[13]

지형 보정은 중력이 측정되는 모든 지점에 대해 계산되어야 하며, 측정 지점과의 고도 차이가 측정 지점으로부터의 거리의 약 5%보다 큰 모든 언덕이나 계곡을 고려해야 한다. 이는 지루하고 시간이 많이 걸리지만 의미 있는 중력 이상을 얻는 데 필요하다.^[13]

3. 4. 완전 부게 이상 (Complete Bouguer anomaly)

단순 부게 이상에 지형 보정(TC)을 추가하여 완전 부게 이상을 구한다.^[13] 지형의 높낮이 변화가 큰 곳에서는 지형 보정이 필수적이다. 완전 부게 이상($\Delta g_{BC}$)은 다음 식으로 계산된다.

:

\Delta g_{BC}=\Delta g_B+TC

여기서 $\Delta g_B$는 단순 부게 이상이다.

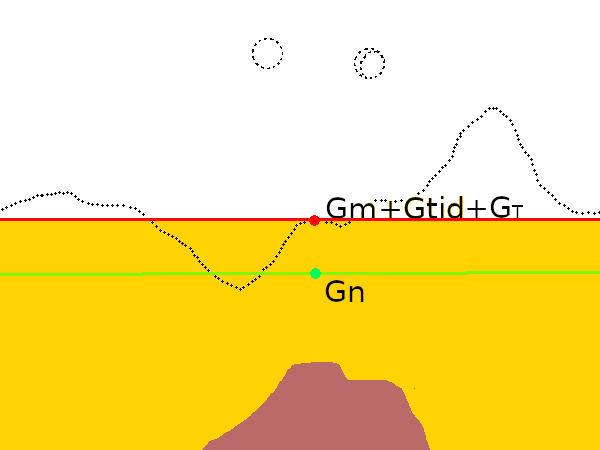
4. 정적 평형 (Isostasy)

지구의 지각과 맨틀이 밀도 차이에 의해 평형을 이루고 있는 상태를 아이소스타시라고 한다.

아이소스타시가 성립하는지 여부는 중력이상을 관측하여 확인할 수 있다.^[4] 자유 공기 이상이 고도에 관계없이 일정해지면 아이소스타시가 성립한다고 볼 수 있다.

중력이상으로부터 지하 구조의 기복을 알 수 있다. 지하에 고밀도의 암석이 있으면 중력값은 표준 중력값보다 커지고, 저밀도의 암석이 있는 경우에는 작아진다. 이러한 중력값 측정을 통해 지하 구조를 추정할 수 있다.

4. 1. 정적 평형 이상 (Isostatic anomaly)

동정적 평형도 참고

부게 이상은 해양 분지에서는 양(+)의 값을, 높은 대륙 지역에서는 음(-)의 값을 갖는다. 이는 해양 분지의 낮은 고도와 대륙의 높은 고도가 깊은 곳의 지각 두께에 의해 보상됨을 보여준다. 높은 지형은 맨틀 위에 "떠 있는" 두꺼운 지각의 부력에 의해 지탱된다.^[4]

'''지각 평형 이상'''은 부게 이상에서 지하 보상에 의한 중력 이상을 뺀 값으로 정의되며, 점성 맨틀의 동적 과정으로 인한 지각 평형에서의 국소적인 편차를 측정하는 척도이다. 평평한 고원의 중심에서는 자유 공기 이상과 대략 같다. 지각 평형 보정은 지각 평형 균형을 계산하는 데 사용되는 지각 평형 모델에 따라 달라지며, 에어리-하이스타넨 모델(지각과 맨틀의 밀도가 균일하고 지각 두께의 변화에 의해 지각 평형 균형이 제공된다고 가정), 프랫-헤이포드 모델(지각 하단이 모든 곳에서 동일한 깊이에 있으며 지각 밀도의 측면 변화에 의해 지각 평형 균형이 제공된다고 가정), 베닝 메이네스 탄성판 모델(지각이 탄성 시트처럼 작용한다고 가정)에 따라 약간씩 다르다.

''순방향 모델링''은 이론적 모델에 의해 요구되는 보상의 상세한 모양을 계산하고 이를 사용하여 부게 이상을 수정하여 지각 평형 이상을 산출하는 과정이다.

5. 중력이상의 원인

중력이상은 지구 내부의 밀도 불균일, 지각 두께 변화, 지형 기복 등 다양한 요인에 의해 발생한다. 지구 중력의 국지적 측정은 행성의 내부 구조를 이해하는 데 도움이 되며, 중력이상에서의 측면적 변화는 지구 내부의 이상 밀도 분포와 관련이 있다.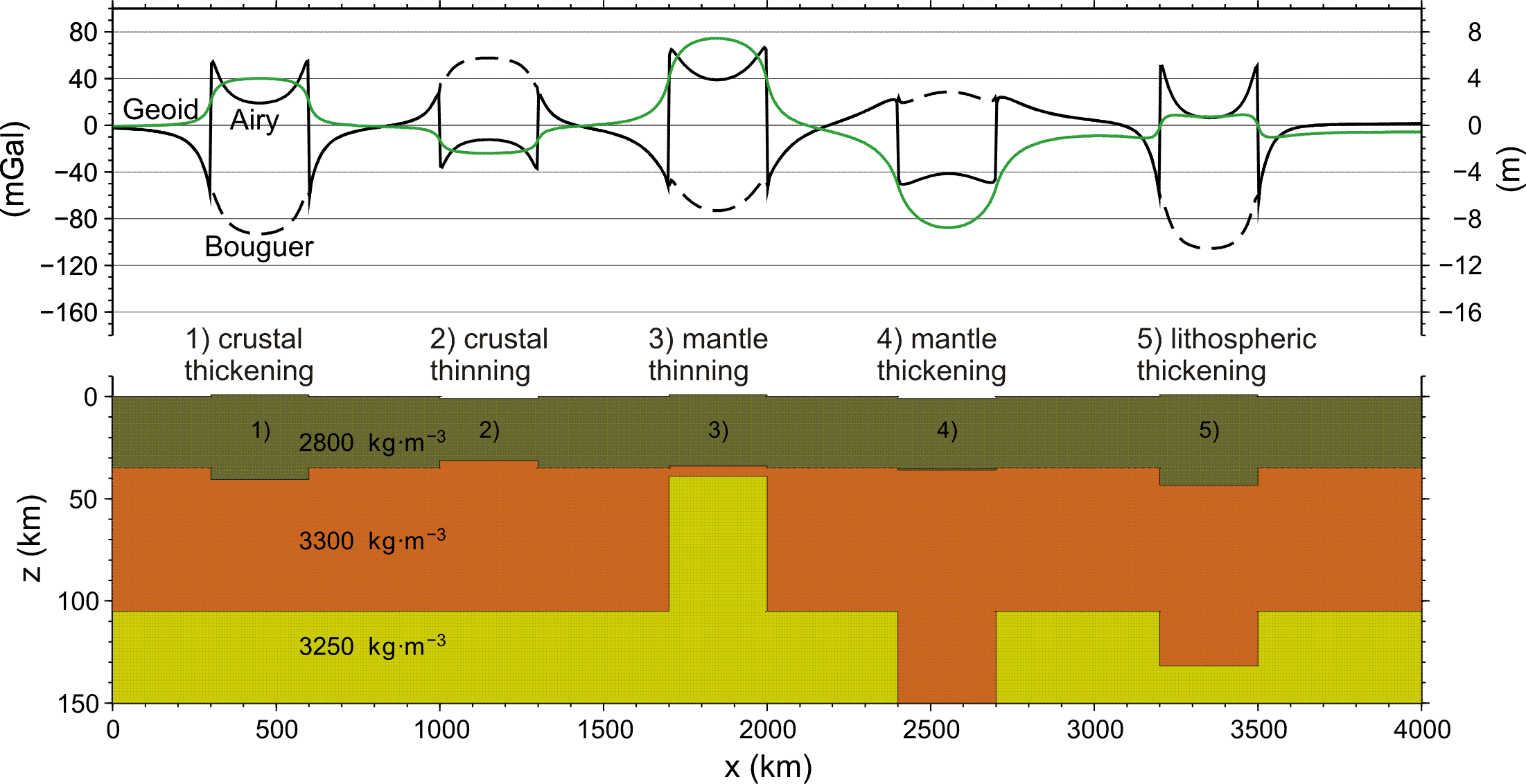

기준 구성에 상대적인 다양한 지각 및 암석권 두께 변화로 인한 중력 및 지오이드 이상. 모든 설정은 기준면보다 +1000m 또는 −1000m의 고도를 가진 국지적인 지각 평형 보상 하에 있다.

5. 1. 지역적 원인 (Regional causes)

대륙의 부게 이상은 일반적으로 음의 값을 가지며, 특히 산맥에서 두드러진다. 예를 들어, 중앙 알프스의 전형적인 부게 이상은 -150밀리갈이다.^[5] 반대로, 부게 이상은 해양에서 양의 값을 가진다. 이러한 이상은 지구 지각의 다양한 두께를 반영한다. 높은 대륙 지형은 밀도가 낮고 두꺼운 지각에 의해 지지되며, 이 지각은 더 밀도가 높은 맨틀 위에 "떠" 있는 반면, 해양 분지는 훨씬 더 얇은 해양 지각으로 덮여 있다.

에어리 정역학적 이상은 완전한 정역학적 보상이 있는 지역에서 0이며, 자유 공기 이상도 지각 블록의 경계 근처를 제외하고 0에 가깝다. 부게 이상은 융기된 지형에서 매우 음의 값을 가진다.

알프스의 부게 이상 지도는 예상되는 깊은 산맥 근원 외에도 추가적인 특징을 보여준다. 양의 이상은 고대 대륙 충돌에 의해 포획된 조밀한 맨틀 암석 쐐기인 이프레아체와 관련이 있다. 몰라세 분지의 저밀도 퇴적물은 음의 이상을 생성한다. 이 지역 전체의 더 큰 조사는 잔존하는 섭입대의 증거를 제공한다. 스위스의 음의 정역학적 이상은 활발한 융기 지역과 상관관계가 있는 반면, 양의 이상은 침강과 관련이 있다.

대서양 중앙 해령에서 자유 공기 이상은 작고 해저 지형과 상관관계가 있다. 해령과 그 측면은 완전히 정역학적으로 보상된 것으로 보인다. 해령 축에서 1000km 이상 떨어진 곳에서는 350mgal 이상의 큰 부게 양의 값을 보이며, 해령 축에서는 200으로 떨어진다. 이는 지진 데이터와 일치하며 해령 축 아래에 저밀도 마그마 챔버가 존재함을 시사한다.

열도 호를 따라 강한 정역학적 및 자유 공기 이상이 나타난다. 이는 섭입대에서 강한 역학적 효과의 징후이다. 자유 공기 이상은 안데스 해안을 따라 약 +70mgal이며, 이는 섭입하는 조밀한 슬래브에 기인한다. 해구 자체는 매우 음의 값을 가지며,^[6] -250mgal보다 더 음의 값을 가진다. 이는 해구를 채우는 저밀도 해양 수와 퇴적물에서 비롯된다.

중력 이상은 암권 깊숙이에서 발생하는 다른 과정에 대한 단서를 제공한다. 예를 들어, 암권 근원의 형성 및 침강은 동톈산 산맥의 음의 정역학적 이상을 설명할 수 있다.^[7] 하와이 중력 이상은 하와이 융기가 아래에 있는 맨틀 플룸과 관련된 연약권 흐름의 산물이라는 설명과 모순되게, 아래에 있는 연약권이 아닌 암권 내에서 완전히 보상되는 것으로 보인다. 대신 융기는 암권의 얇아짐의 결과일 수 있다.

중력이상을 관측하여 아이소스타시가 성립하는지 여부를 확인할 수 있다. 아이소스타시가 성립하고 있을 때는 자유 공기 이상이 고도에 관계없이 일정해진다. 중력이상으로부터 지하 구조의 기복을 알 수 있으며, 지하에 고밀도의 암석이 있으면 중력값은 표준 중력값보다 커지고, 저밀도의 암석이 있는 경우에는 작아진다. 이것들로부터 중력값을 측정하여 지하 구조를 추정할 수 있다.

5. 2. 국지적 원인 (Local anomalies)

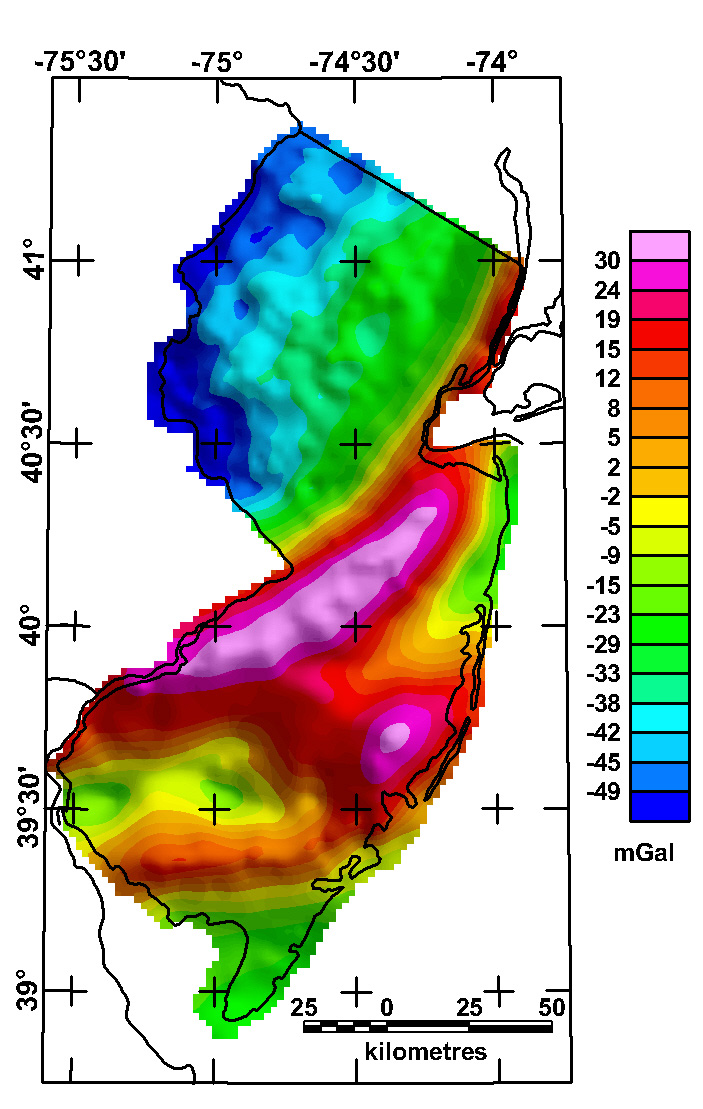
광체, 단층, 염돔 등 비교적 작은 규모의 지질 구조는 국지적인 중력이상을 발생시킨다. 예를 들어, 금속 광체는 주변 암석보다 밀도가 높아 양의 중력이상을 유발한다. 반대로, 염돔은 주변 암석에 비해 밀도가 낮기 때문에 중력 지도에서 낮은 값으로 표시되어 음의 중력이상을 나타낸다.^[9]

전체 산맥과 광체 사이의 규모에서 부게 이상은 암석 유형을 나타낼 수 있다. 예를 들어, 뉴저지 중부를 가로지르는 북동-남서 방향의 높은 값은 밀도가 높은 현무암으로 채워진 트라이아스기 시대의 단층곡을 나타낸다.^[9]

중력이상을 관측하여 아이소스타시가 성립하는지 여부를 확인할 수 있다. 아이소스타시가 성립할 때는 자유 공기 이상이 고도에 관계없이 일정해진다.

중력이상으로부터 지하 구조의 기복을 알 수 있으며, 지하에 고밀도의 암석이 있으면 중력값은 표준 중력값보다 커지고, 저밀도의 암석이 있는 경우에는 작아진다. 이것들로부터 중력값을 측정하여 지하 구조를 추정할 수 있다.

6. 중력이상의 활용

중력이상은 물리 탐사 방법 중 하나로 사용된다.^[9]

6. 1. 지구물리학적 연구

중력이상을 관측하여 아이소스타시가 성립하는지 여부를 확인할 수 있다. 아이소스타시가 성립하고 있을 때는 자유 공기 이상이 고도에 관계없이 일정해진다.

중력이상으로부터 지하 구조의 기복을 알 수 있으며, 지하에 고밀도의 암석이 있으면 중력값은 표준 중력값보다 커지고, 저밀도의 암석이 있는 경우에는 작아진다. 이것들로부터 중력값을 측정하여 지하 구조를 추정할 수 있다.

6. 2. 자원 탐사

중력 이상 탐사는 응용 지구물리학에서 물리 탐사 방법 중 하나로 사용된다. 예를 들어, 국지적인 양의 중력 이상은 밀도가 높은 금속 광석 덩어리를 나타낼 수 있다. 반대로, 염상은 주변 암석에 비해 밀도가 낮은 소금으로 구성되어 있어 일반적으로 중력 지도에서 낮은 값으로 표시된다.^[9]

규모가 큰 경우에는 부게 이상을 통해 암석 유형을 파악할 수 있다. 예를 들어, 뉴저지 중부를 가로지르는 북동-남서 방향의 높은 중력 이상 값은 밀도가 높은 현무암으로 채워진 트라이아스기 시대의 단층곡을 나타낸다.^[9] 이러한 정보를 바탕으로 광물 자원, 석유, 천연가스 등의 매장 가능성이 높은 지역을 예측할 수 있다.

6. 3. 우주물리학적 이용

천문학, 특히 우주물리학에서 중력이상은 특정 우주 영역의 중력 관측값과 이론값(질량 공간 밀도의 예측값으로 계산)의 차이를 의미한다. 중력이상의 존재는 해당 우주 영역의 실제 질량 공간 밀도 분포가 예측값과 다르다는 것을 의미한다.

이러한 중력이상은 몇 가지 발견되었는데, 예를 들어 우리 자신의 은하의 관측된 회전 운동 특성은, 보이는(광학적으로 관측할 수 있는) 물질이 만드는 중력만으로는 설명되지 않아, 그 10배 정도의 보이지 않는 무언가에 기인하는 질량에 상당하는 것이 필요하다는 점에서 가설상의 존재로서 "암흑 물질"이라는 명칭으로 연구되고 있다. 또한, 은하간 공간의 중력 값은 은하의 고유 속도(peculiar velocity)의 관측값으로 계산되지만, 이로부터 바다뱀자리와 센타우루스자리 방향, 은하로부터 에서 거리에 거대 인력체(Great Attractor)라고 불리는 중력이상이 발견되었다.

7. 인공위성을 이용한 중력 측정

인공위성을 이용한 중력 측정(Satellite gravimetry)은 지구 중력장의 측정을 수행하기 위해 인공위성을 사용하는 것이다. 이러한 측정을 통해 지구의 중력장에 대한 정보를 얻을 수 있으며, 이는 지구 물리학 및 측지학 연구에 유용하게 활용된다.

인공위성을 이용한 중력 측정 방법은 다음과 같다.

궤도 섭동 분석: 인공위성의 궤도 변화를 정밀하게 측정하여 중력장의 영향을 분석한다.
인공위성 고도계: 인공위성에서 지표면까지의 거리를 측정하여 중력장의 변화를 추정한다.
인공위성-인공위성 추적: 두 대의 인공위성 간의 거리를 측정하여 중력장의 변화를 감지한다.

이러한 방법들을 통해 지구의 중력장을 고해상도로 측정하고, 해양 지형, 대륙 지각 구조, 극지방의 얼음 질량 변화 등을 연구할 수 있다. 대표적인 인공위성 중력 측정 프로젝트로는 GRACE와 GOCE가 있다.

참조

_[1] 서적 Glossary of geology. American Geological Institute 1997
_[2] 서적 Fundamentals of geophysics Cambridge University Press 2007
_[3] 서적 A dictionary of geology and earth sciences Oxford University Press 2013
_[4] 서적 Global tectonics. Wiley-Blackwell 2009
_[5] 간행물 Gravity anomalies and dynamics of the Swiss Alps 1985-08
_[6] 서적 Physical geology : exploring the Earth West Pub. Co 1992
_[7] 간행물 Gravity anomalies, the deep structure, and dynamic processes beneath the Tien Shan 1990-01-01
_[8] 간행물 Island subsidence, hot spots, and lithospheric thinning 1978
_[9] 서적 Igneous processes during the assembly and breakup of Pangaea: Northern New Jersey and New York City: 30th Annual Meeting of the Geological Association of New Jersey https://www.research[...] College of Staten Island 2022-01-29
_[10] 논문 Somigliana–Pizzetti gravity: the international gravity formula accurate to the sub-nanoGal level. 2001
_[11] 논문 Free-air correction in gravity anomaly interpretation. 1987
_[12] 논문 Determination of the Bouguer correction constant. 1942
_[13] 논문 Bouguer corrections with varying surface density. 1956

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com