맨위로가기

틀 끌림

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

틀 끌림은 일반 상대성 이론에서 예측되는 현상으로, 회전하는 질량이 주변 시공간을 끌어당기는 효과를 의미한다. 오스트리아의 요제프 렌제와 한스 티링은 1918년 이 현상을 처음 수식화했으며, 렌제-티링 효과로 알려져 있다. 틀 끌림은 알베르트 아인슈타인이 일반 상대성 이론을 통해 예측했지만, 오랫동안 검증 수단이 없어 확인되지 못했다. 이후 LAGEOS 위성과 중력탐사B 위성을 이용한 실험을 통해 렌제-티링 효과가 측정되었으며, 일반 상대성 이론의 예측과 일치하는 결과가 확인되었다. 틀 끌림은 블랙홀 주변 별의 궤도 운동, 상대론적 제트 현상 등 천문학적 현상에도 영향을 미친다.

2. 역사

틀 끌림은 오스트리아의 요제프 렌제(Josef Lensede)와 한스 티링(Hans Thirringde)이 처음 수식화했고, 렌제-티링 효과로 알려져 있다.[49] 알베르트 아인슈타인이 일반 상대성 이론의 현상으로 예측했지만, 오랫동안 검증 수단이 없어 그 존재를 검증할 수 없었다. 천체가 시공간을 휘게 하여 중력을 발생시킨다는 이 이론은, 회전하는 질량이 마치 당밀 속 회전하는 팽이처럼 주변 공간을 끌어당긴다고 예측한다.[49] 이 현상은 1918년 오스트리아 물리학자 요제프 렌제와 한스 티링이 예측했다.[49] 오랫동안 검증 수단이 없었지만, I. 치우폴리니와 E. C. 파블리스는 레이저 거리 측정 장치로 NASA의 LAGEOS와 LAGEOS 2 위성 궤도를 11년간 정밀하게 기록하여, 위성 위치가 매년 3m 이하로 어긋남을 확인했다.[49] 이후, NASA의 Gravity Probe B가 미세한 천문학적 섭동을 더 정밀하게 측정했다.[50]

2. 1. 초기 연구

틀 끌림의 첫 번째 수식화는 오스트리아의 요제프 렌제(Josef Lensede)와 한스 티링(Hans Thirringde)에 의해 이루어졌고, 렌제-티링 효과로 알려져 있다.[49] 알베르트 아인슈타인이 일반 상대성 이론의 현상으로 예측했지만, 오랫동안 검증 수단이 없어 그 존재를 검증할 수 없었다.

일반 상대성 이론은 천체에 의해 발생하는 시공간의 휨으로 중력을 기술하며, 회전하는 질량이 당밀 속에 놓인 회전하는 팽이처럼 그 주변의 공간을 끌어당기는 것도 예언한다.[49] 이 현상은 1918년 오스트리아의 물리학자인 요제프 렌제와 한스 티링에 의해 예측되었다.[49] 오랫동안 검증 수단이 없었지만, I. 치우폴리니와 E. C. 파블리스는 레이저 거리 측정 장치를 사용하여 NASA의 두 위성 LAGEOS와 LAGEOS2의 궤도를 11년에 걸쳐 수 mm의 정밀도로 기록함으로써 이 끌어당김 효과를 관측하여 위성의 위치가 매년 3m 이하의 거리만큼 어긋나는 것을 밝혀냈다.[49] 후에 미소한 천문학적 섭동을 훨씬 고정밀도로 측정하기 위해 설계된 NASA의 Gravity Probe B에 의해 상세히 조사되었다.[50]

2. 2. 실험적 검증

1976년, 반 패튼과 에버릿은 지구 극궤도에 두 쌍의 반대 방향으로 공전하는 우주선을 배치하여 렌제-티링 효과를 측정하는 임무를 제안했다.[7][8] 1986년, 치우폴리니는 LAGEOS 위성과 유사한 궤도를 가진 위성을 발사하여 렌제-티링 효과를 측정하는 아이디어를 제안했다.[9]

1977년부터 1978년까지, LAGEOS 위성과 위성 레이저 거리 측정 (SLR) 기술을 사용하여 렌제-티링 효과를 측정하려는 첫 제안이 있었다.[10] 1996년, LAGEOS와 LAGEOS II 위성을 사용하여 실제로 렌제-티링 효과 측정이 시작되었다.[11] I. 치우폴리니와 E. C. 파블리스는 레이저 거리 측정 장치를 사용하여 NASA의 두 위성 LAGEOS와 LAGEOS2의 궤도를 11년에 걸쳐 수 mm의 정밀도로 기록함으로써 이 끌어당김 효과를 관측하여 위성의 위치가 매년 3m 이하의 거리만큼 어긋나는 것을 밝혀냈다.[49]

2004년 4월, 미국 항공우주국(NASA)의 중력탐사B 위성이 발사되어 일반 상대성 이론의 예측, 특히 측지 현상과 틀 끌림을 정밀하게 측정하였다.[51] 2011년, 중력탐사B의 최종 결과가 발표되었으며, 측정 결과는 틀 끌림 현상을 포함하여 일반 상대성 이론의 예측과 일치하는 것으로 확인되었다.[52][53]

LAGEOS 위성을 사용한 실험 결과의 정확성에 대해서는 논란의 여지가 있다.[17][18][19]

3. 효과

틀 끌림은 일반 상대성 이론 및 회전하는 거대한 물체 근처에서 나타나는 유사 이론의 현상이다. 렌제-티링 효과에 따르면, 멀리 떨어진 관찰자가 볼 때 물체를 중심으로 회전하는 기준틀에서 시계가 가장 빠르게 간다. 물체의 회전 방향으로 이동하는 빛은 회전에 반대 방향으로 이동하는 빛보다 더 빠르게 거대한 물체를 지나간다. 정성적으로 틀 끌림은 전자기 유도의 중력 유사물로 볼 수 있다.[1] 내부 영역은 외부 영역보다 더 많이 끌려, 흥미로운 국소 회전틀을 생성한다.

틀 끌림 효과는 오스트리아의 요제프 렌제(Josef Lensede)와 한스 티링(Hans Thirringde)에 의해 처음 수식화되었으며, 렌제-티링 효과로 알려져 있다. 이 효과는 주로 커 계량을 사용하여 유도된다. 커 계량은 각운동량 ''J''를 가지고 회전하는 질량 ''M'' 근처 시공간의 기하를 묘사한다. 비상대론적 극한에서 커 계량은 편원 좌표계에서의 직교 계량이 된다. 커 계량은 각속도 Ω를 가지고 동시에 회전하는 관성계와 일치하는데, 이때 Ω는 반지름 r과 고도 θ에 의존하며, 적도 면에서 Ω는 간단한 식으로 표현된다. 따라서 관성 좌표계는 회전하는 질량 중심에 대하여 그것과 같은 방향으로 회전하는 이끌림 효과를 받게 되는데, 이것이 틀 끌림이다.

회전하는 구형 껍질 내부에서 렌즈-티링 효과로 인한 가속도는 특정 계수들을 사용하여 계산할 수 있다.[47] 회전하는 구형 껍질 내부의 시공간은 평평하지 않지만, 껍질이 정확한 구형에서 벗어나고 껍질 내부의 질량 밀도가 달라지도록 허용되는 경우에는 평평한 시공간이 가능하다.[48]

알베르트 아인슈타인은 일반 상대성 이론의 현상으로 틀 끌림을 예측했지만, 오랫동안 검증 수단이 없어 그 존재를 검증할 수 없었다. 회전하는 질량이 그 주변의 공간을 끌어당기는 현상은 레이저 거리 측정 장치를 사용하여 NASA의 두 위성 LAGEOS와 LAGEOS2의 궤도를 관측함으로써 확인되었다.[49]

3. 1. 중력자기와 유성 기어 시스템

틀 끌림은 회전하는 거대한 물체 근처에서 나타나는 현상으로, 일반 상대성 이론에서 예측된다. 이 효과는 중력 탐사 B 실험을 통해 검증되기도 했다. 정성적으로, 틀 끌림은 전자기 유도의 중력 유사물로 이해할 수 있다.[1]

회전하는 블랙홀 근처에 있는 스케이트 선수를 예로 들어보자. 블랙홀을 향해 뻗은 팔은 중력 자기 유도에 의해 회전 방향으로 힘을 받는다. 반대로 블랙홀에서 멀리 떨어진 팔은 반회전 방향으로 힘을 받는다. 이는 일상 경험과는 반대되는 현상이다.[1]

스케이트 선수가 팔을 뻗을 때 특정 속도로 회전하면, 관성 효과와 틀 끌림 효과가 균형을 이루어 회전 속도가 변하지 않는다. 등가 원리에 따르면 중력 효과는 국소적으로 관성 효과와 구별할 수 없으므로, 이 회전 속도는 비회전에 대한 국소 참조가 된다. 이 기준틀은 멀리 떨어진 별에 대해 회전하고 블랙홀에 대해 반회전한다.[1]

이러한 현상은 핵 스핀으로 인한 원자 스펙트럼의 초미세 구조와 유사하며, 유성 기어 시스템으로 비유할 수 있다. 블랙홀은 태양 기어, 스케이트 선수는 행성 기어, 외부 우주는 링 기어에 해당한다. 마흐의 원리를 참고할 수 있다.[1]

3. 2. 적도 궤도에서의 무게 변화

적도 궤도에 있지만 자유 낙하 상태가 아닌 물체는 회전 방향에 따라 무게가 다르게 느껴진다. 반회전 방향으로 궤도를 돌면 무게가 더 나가고, 회전 방향으로 궤도를 돌면 무게가 덜 나간다. 예를 들어, 적도에 있는 볼링장에서 볼링공을 반회전 방향으로 굴리면, 같은 볼링공을 회전 방향으로 굴릴 때보다 더 무겁게 느껴진다.

틀 끌림은 볼링공을 가속하거나 감속시키지 않으며, "점성"과는 다르다. 정지된 수직 추는 회전하는 물체 위에 매달려도 기울어지지 않고 수직으로 유지된다.

3. 3. 정지된 물체의 기울어짐

회전하는 물체 위에 매달린 정지된 수직 추는 기울어지지 않고 수직으로 걸린다. 만약 떨어지기 시작하면, 유도에 의해 회전 방향으로 밀려난다.

3. 4. 선형 틀 끌림과 정적 질량 증가

선형 틀 끌림은 선형 운동량에 적용되는 일반 상대성 이론의 결과이다. 비록 회전 틀 끌림과 이론적으로 동등한 타당성을 갖지만, 실험적 검증의 어려움 때문에 관련 논의가 훨씬 적고 틀 끌림에 대한 기사에서 종종 생략된다.

정적 질량 증가는 다른 질량이 근처에 놓일 때 물체의 관성이 증가하는 현상이다. 아인슈타인은 정적 질량 증가가 틀 끌림과 같은 방정식에서 파생된다는 것을 증명했지만, 이 역시 실험적으로 확인하기는 어렵다.

4. 수학적 설명

틀 끌림은 주로 커 계량을 사용하여 유도된다. 커 계량은 각운동량 ''J''를 가지고 회전하는 질량 ''M'' 근처 시공간의 기하를 묘사한다. 커 계량은 다음과 같이 표현된다.[41][42]

:

c^{2} d\tau^{2} =

\left( 1 - \frac{r_{s} r}{\rho^{2}} \right) c^{2} dt^{2}


  • \frac{\rho^{2}}{\Lambda^{2}} dr^{2}
  • \rho^{2} d\theta^{2}



::::

  • \left( r^{2} + \alpha^{2} + \frac{r_{s} r \alpha^{2}}{\rho^{2}} \sin^{2} \theta \right) \sin^{2} \theta \ d\phi^{2}

+ \frac{2r_{s} r\alpha c \sin^{2} \theta }{\rho^{2}} d\phi dt



이때 ''r''''s''는 슈바르츠실트 반지름

:

r_{s} = \frac{2GM}{c^{2}}



이며, \alpha, \rho^{2}, \Lambda^{2}는 다음과 같이 주어진다.

:

\alpha =J/Mc\,,



:

\rho^{2} = r^{2} + \alpha^{2} \cos^{2} \theta\,,\!



:

\Lambda^{2} = r^{2} - r_{s} r + \alpha^{2}\,.



''M''(또는 ''r''''s'')이 영으로 가는 비상대론적 극한에서, 커 계량은 편원 좌표계에서의 직교 계량

:

c^{2} d\tau^{2} =

c^{2} dt^{2}

  • \frac{\rho^{2}}{r^{2} + \alpha^{2}} dr^{2}
  • \rho^{2} d\theta^{2}
  • \left( r^{2} + \alpha^{2} \right) \sin^{2}\theta d\phi^{2}



이 된다.

이것은 커 계량에서

:

c^{2} d\tau^{2} =

\left( g_{tt} - \frac{g_{t\phi}^{2}}{g_{\phi\phi}} \right) dt^{2}

+ g_{rr} dr^{2} + g_{\theta\theta} d\theta^{2} +

g_{\phi\phi} \left( d\phi + \frac{g_{t\phi}}{g_{\phi\phi}} dt \right)^{2}



으로 쓸 수 있다.

이 계량은 반지름 r과 고도 θ에 의존하는 각속도 Ω를 가지고 동시에 회전하는 관성계와 일치하는데, 이 때 Ω는

:

\Omega = -\frac{g_{t\phi}}{g_{\phi\phi}} = \frac{r_{s} \alpha r c}{\rho^{2} \left( r^{2} + \alpha^{2} \right) + r_{s} \alpha^{2} r \sin^{2}\theta}



와 같다.

이것은 적도 면에서

:

\Omega = \frac{r_{s} \alpha c}{r^{3} + \alpha^{2} r + r_{s} \alpha^{2}}

[43]

로 간단히 된다. 그러므로 관성 좌표계는 회전하는 질량 중심에 대하여 그것과 같은 방향으로 회전하는 이끌림 효과를 받게 되는데, 이것이 틀 끌림이다.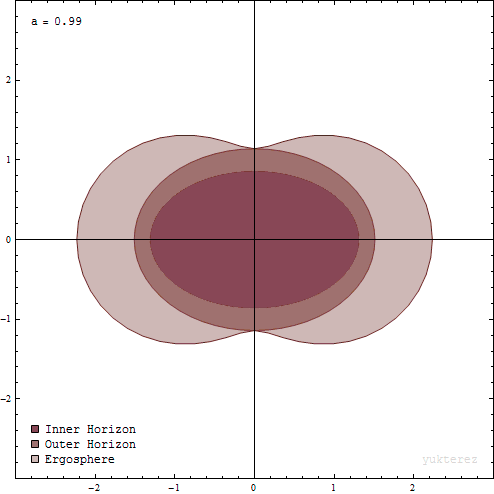

300px


틀 끌림의 극단적인 형태는 회전하는 블랙홀의 에르고스피어 내에서 발생한다. Kerr 계량은 특이점을 갖는 것처럼 보이는 두 표면을 가지고 있다. 내부 표면은 슈바르츠실트 계량에서 관찰되는 것과 유사한 구형 사건의 지평선에 해당한다. 이는 다음과 같은 지점에서 발생한다.

:

r_\text{inner} = \frac{r_{s} + \sqrt{r_{s}^{2} - 4\alpha^{2}}}{2}



여기서 계량의 순수 방사형 성분 ''grr''은 무한대로 간다. 외부 표면은 낮은 스핀 매개변수를 가진 편구면으로 근사될 수 있으며, 더 높은 스핀 매개변수를 가진 호박 모양[44][45]과 유사하다. 이 표면은 회전 축의 극점에서 내부 표면에 닿으며, 여기서 위도 ''θ''는 0 또는 π와 같다. Boyer-Lindquist 좌표계에서 이 표면의 반경은 다음 공식으로 정의된다.

:

r_\text{outer} = \frac{r_{s} + \sqrt{r_{s}^{2} - 4\alpha^{2} \cos^{2}\theta}}{2}


5. 천문학적 증거

상대론적 제트는 틀 끌림의 실체를 증명하는 증거가 될 수 있다. 렌스-티링 효과에 의해 생성된 중력자기력(틀 끌림)과 회전하는 블랙홀의 에르고스피어 내의 결합[37][38]은 로저 펜로즈가 제시한 에너지 추출 메커니즘[39]과 결합되어 상대론적 제트의 관찰된 특성을 설명하는 데 사용되어 왔다. 레바 케이 윌리엄스가 개발한 중력자기 모델은 퀘이사와 활동 은하핵에서 방출되는 관찰된 고에너지 입자(~GeV)를 예측하며, X선, γ선, 상대론적 e−– e+ 쌍의 추출, 극축을 중심으로 하는 정렬된 제트, 제트의 비대칭적 형성(궤도면에 상대적)을 설명한다.

렌스-티링 효과는 거대한 백색 왜성과 펄서로 구성된 이진 시스템에서 관찰되었다.[40]

참조

[1] 논문 Über die Wirkung rotierender ferner Massen in der Einsteinschen Gravitationstheorie 1918
[2] 논문 Berichtigung zu meiner Arbeit: 'Über die Wirkung rotierender Massen in der Einsteinschen Gravitationstheorie' 1921
[3] 논문 Über den Einfluss der Eigenrotation der Zentralkörper auf die Bewegung der Planeten und Monde nach der Einsteinschen Gravitationstheorie 1918
[4] 논문 General-relativistic rotation laws in rotating fluid bodies
[5] 서적 The Meaning of Relativity
[6] 서적 The Meaning of Relativity Chapman and Hall 1987
[7] 논문 Possible Experiment with Two Counter-Orbiting Drag-Free Satellites to Obtain a New Test of Einsteins's General Theory of Relativity and Improved Measurements in Geodesy
[8] 논문 A possible experiment with two counter-rotating drag-free satellites to obtain a new test of Einstein's general theory of relativity and improved measurements in geodesy
[9] 논문 Measurement of Lense–Thirring Drag on High-Altitude Laser-Ranged Artificial Satellites
[10] 논문 Relativistic Effects on the Motion of Earth's Artificial Satellites
[11] 논문 Measurement of dragging of inertial frames and gravitomagnetic field using laser-ranged satellites
[12] 논문 On a new method to measure the gravitomagnetic field using two orbiting satellites
[13] 논문 A confirmation of the general relativistic prediction of the Lense–Thirring effect
[14] 논문 Determination of frame-dragging using Earth gravity models from CHAMP and GRACE
[15] 논문 The Impact of the New Earth Gravity Models on the Measurement of the Lense-Thirring Effect 2004
[16] 논문 History of the attempts to measure orbital frame-dragging with artificial satellites 2013
[17] 논문 Some reflections on the Lageos frame-dragging experiment in view of recent data analyses 2014
[18] 논문 Phenomenology of the Lense-Thirring effect in the solar system 2011
[19] 논문 Testing gravitational physics with satellite laser ranging 2011
[20] 간행물 The Gyroscope Experiment I. General Description and Analysis of Gyroscope Performance. In: Bertotti, B. (Ed.), ''Proc. Int. School Phys. "Enrico Fermi" Course LVI'' New Academic Press
[21] 간행물 Gravity Probe B: Countdown to Launch. In: Laemmerzahl, C.; Everitt, C. W. F.; Hehl, F. W. (Eds.), ''Gyros, Clocks, Interferometers...: Testing Relativistic Gravity in Space'' Springer
[22] 간행물 Proposal for a Satellite Test of the Coriolis Prediction of General Relativity, ''WSEG, Research Memorandum No. 11''
[23] 논문 On Experimental Tests of the General Theory of Relativity
[24] 논문 Prospects for an improved Lense–Thirring test with SLR and the GRACE gravity mission https://cddis.nasa.g[...] 2003
[25] 간행물 Gravity Probe B Experiment Error, ''poster L1.00027 presented at the American Physical Society (APS) meeting in Jacksonville, Florida, on 14–17 April 2007''
[26] 웹사이트 StanfordNews 4/14/07 https://einstein.sta[...] 2019-09-27
[27] 웹사이트 Report of the 2008 Senior Review of the Astrophysics Division Operating Missions http://nasascience.n[...] 2009-03-20
[28] 웹사이트 Gravity Probe B scores 'F' in NASA review https://www.newscien[...] 2023-09-17
[29] 웹사이트 Gravity Probe B – MISSION STATUS http://einstein.stan[...]
[30] 웹사이트 Gravity Probe B finally pays off http://www.sciencene[...] 2011-05-07
[31] 뉴스 Gravity Probe B: Final results of a space experiment to test general relativity http://prl.aps.org/a[...] 2011-05-06
[32] 웹사이트 As World Turns it Drags Time and Space https://www.nasa.gov[...] Goddard Space Flight Center 2019-08-23
[33] 웹사이트 Gravity Probe B https://www.nasa.gov[...] NASA Headquarters 2019-08-23
[34] 논문 A test of general relativity using the LARES and LAGEOS satellites and a GRACE Earth gravity model: Measurement of Earth's dragging of inertial frames
[35] 논문 Testing Properties of the Galactic Center Black Hole Using Stellar Orbits
[36] 논문 Testing the General Relativistic "No-Hair" Theorems Using the Galactic Center Black Hole Sagittarius A*
[37] 논문 Extracting X rays, Ύ rays, and relativistic e−– e+ pairs from supermassive Kerr black holes using the Penrose mechanism 1995
[38] 논문 Collimated escaping vortical polar e−–e+ jets intrinsically produced by rotating black holes and Penrose processes 2004
[39] 논문 Gravitational collapse: The role of general relativity 1969
[40] 논문 Lense–Thirring frame dragging induced by a fast-rotating white dwarf in a binary pulsar system 2020-01-31
[41] 논문 Gravitational field of a spinning mass as an example of algebraically special metrics 1963
[42] 서적 The Classical Theory of Fields (Course of Theoretical Physics, Vol. 2) Pergamon Press 1975
[43] 논문 Detection of the gravitometric clock effect 2008
[44] Arxiv The Kerr spacetime: A brief introduction
[45] 서적 Black Holes: A Very Short Introduction https://books.google[...] Google books
[46] 서적 Gravitation
[47] 논문 On the history of the so-called Lense–Thirring effect http://philsci-archi[...] 2005
[48] 논문 Induction of correct centrifugal force in a rotating mass shell 1985
[49] 논문 空間の引きずり効果を確認 http://www.natureasi[...] 2004-10-21
[50] 논문 アインシュタインの一般相対性理論を実証する証拠をまた1つ発見 https://www.astroart[...] 2011-05-09
[51] 뉴스 우주는 ‘시공간’…아인슈타인이 옳았다 http://news.khan.co.[...] 경향신문 2007-04-15
[52] 저널 인용 Gravity Probe B: Final Results of a Space Experiment to Test General Relativity
[53] 뉴스 1세기 전 아인슈타인 가설, 다 맞았다 http://biz.chosun.co[...] 조선비즈 2011-05-24


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com