맨위로가기

페르미 준위

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

페르미 준위는 전압 측정, 고체의 띠 구조, 비평형 상태 등 다양한 맥락에서 사용되는 물리학 용어이다.

페르미 준위는 전자의 화학 퍼텐셜을 나타내며, 회로의 두 지점 사이의 전압 차이와 관련된다. 열역학적 평형 상태에서 페르미 준위는 연결된 회로 전체에서 일정하게 유지된다. 고체의 띠 이론에서 페르미 준위는 전자가 채워질 확률을 나타내며, 재료의 전기적 특성을 결정하는 데 중요한 역할을 한다. 절연체, 금속, 반도체 등 재료의 종류에 따라 페르미 준위의 위치가 다르다.

비평형 상태에서는 준페르미 준위가 사용될 수 있으며, 시스템의 화학적 불균형, 변화하는 전자기장, 온도 변화 등 다양한 요인에 의해 영향을 받는다. 페르미 준위는 "띠 기준 페르미 준위"와 혼동될 수 있으며, "페르미 에너지"와도 구분되어야 한다. 페르미 준위는 에너지의 기준점을 설정하는 데 사용되며, 작은 시스템에서는 전하 효과로 인해 정의가 복잡해질 수 있다.

더 읽어볼만한 페이지

  • 띠 이론 - 띠구조
    띠구조는 결정 내 전자의 에너지 범위를 나타내는 개념으로, 에너지 띠와 띠틈으로 구성되며, 도체, 절연체, 반도체의 전기적 특성을 결정하는 데 중요한 역할을 한다.
  • 띠 이론 - 띠틈
    띠틈은 반도체와 절연체에서 전자가 존재할 수 없는 에너지 준위 범위로, 물질의 전기적, 광학적 특성을 결정하며 직접 띠틈과 간접 띠틈으로 나뉘고, 띠틈 엔지니어링을 통해 제어 가능하다.
  • 컴퓨터에 관한 - N형 반도체
    N형 반도체는 전자를 주된 전하 운반체로 사용하는 반도체이다.
  • 컴퓨터에 관한 - CMOS
    CMOS는 상보적 금속 산화막 반도체의 약자로, 저전력 소비를 특징으로 하며, P형과 N형 MOSFET을 결합하여 논리 게이트를 구현하는 디지털 회로 설계 방식 및 공정 계열이다.
  • 반도체 - N형 반도체
    N형 반도체는 전자를 주된 전하 운반체로 사용하는 반도체이다.
  • 반도체 - 띠구조
    띠구조는 결정 내 전자의 에너지 범위를 나타내는 개념으로, 에너지 띠와 띠틈으로 구성되며, 도체, 절연체, 반도체의 전기적 특성을 결정하는 데 중요한 역할을 한다.
페르미 준위
페르미 준위
정의고체 내에서 전자가 점유할 수 있는 에너지 준위 중 가장 높은 에너지 준위이다. 절대 영도에서 전자가 채워져 있는 가장 높은 에너지 준위를 의미한다.
물리적 의미
개요페르미 준위는 고체 내에서 전자의 분포를 설명하는 데 중요한 개념이다.
페르미 준위는 고체의 전기 전도도와 열전도도 같은 성질을 이해하는 데 필수적이다.
반도체반도체에서는 페르미 준위가 가전자대와 전도대 사이의 에너지 띠 간격 내에 위치한다.
페르미 준위의 위치는 도핑에 따라 변하며, 반도체의 전기적 특성을 조절하는 데 사용된다.
수학적 표현
페르미 에너지페르미 준위는 종종 페르미 에너지로 표현된다.
페르미 에너지(E_F)는 페르미 준위에서 전자가 가질 수 있는 최대 에너지 값이다.
페르미-디락 분포 함수전자가 페르미 준위에 따라 분포되는 확률을 나타내는 함수이다.
페르미-디락 분포 함수는 온도에 따라 전자의 에너지 분포가 어떻게 변하는지를 보여준다.
공식'' (제공된 수식)
관련 항목
관련 주제페르미 에너지
페르미-디락 통계
띠 이론
고체물리학
양자역학
참고 문헌
참고 서적Introduction to Solid State Physics, Charles Kittel, Wiley ()
참고 웹사이트Fermi level ( physics Britannica |url=https://www.britannica.com/science/Fermi-level |access-date=2023-06-03 |website=www.britannica.com |language=en}})

2. 전압 측정과 페르미 준위

전압계는 페르미 준위의 차이를 전자 전하로 나눈 값을 측정한다.


전류는 정전기적 전위(갈바니 전위)의 차이로 발생한다고 알려져 있지만, 항상 그런 것은 아니다.[3] 예를 들어, pn 접합과 같은 여러 재료로 만들어진 소자는 평형 상태에서 내부 정전기적 전위차를 가지지만, 순 전류는 흐르지 않는다. 전압계를 접합부에 연결하면 0볼트를 측정한다.[4] 즉, 정전기적 전위만이 물질 내 전하 흐름에 영향을 미치는 유일한 요소는 아니다. 파울리 반발, 캐리어 농도 기울기, 전자기 유도 및 열 효과도 중요한 역할을 한다.

전자 회로에서 측정되는 '전압'은 전자의 화학퍼텐셜(페르미 준위)과 관련이 있다. 전압계의 리드를 회로의 두 점에 연결하면 표시되는 전압은 단위 전하가 한 점에서 다른 점으로 이동할 때 전달되는 총 일의 척도이다. 서로 다른 전압의 두 점 사이에 단순한 와이어를 연결하면(단락 회로) 전류가 양의 전압에서 음의 전압으로 흘러 사용 가능한 일을 열로 변환한다.

물체의 페르미 준위는 전자를 추가하는 데 필요한 일, 또는 전자를 제거하여 얻는 일을 나타낸다. 따라서 전자 회로의 두 점 ''A''와 ''B'' 사이에서 관찰되는 전압 차이 ''V''A − ''V''B는 페르미 준위에서 해당 화학퍼텐셜 차이 ''μ''A − ''μ''B와 다음 공식으로 정확하게 관련된다.[5]

: ''V''A - ''V''B = (''μ''A - ''μ''B)/(-''e'')

여기서 −''e''는 전자 전하이다.

전자는 높은 ''μ''(낮은 전압)의 물체에서 낮은 ''μ''(높은 전압)으로 이동한다. 이 전자 흐름은 낮은 ''μ''를 증가시키고 높은 ''μ''를 감소시킨다. 결국 ''μ''는 두 물체 모두에서 동일한 값으로 안정된다.

2. 1. 열역학적 평형 상태



전류는 정전기적 전위(갈바니 전위)의 차이에 의해 발생한다고 알려져 있지만, 항상 그런 것은 아니다.[3] 예를 들어, pn 접합과 같은 다중 재료 소자는 평형 상태에서 내부 정전기적 전위차를 가지지만, 순 전류는 흐르지 않는다. 전압계를 접합부에 연결하면 0볼트를 측정한다.[4] 즉, 정전기적 전위만이 물질 내 전하 흐름에 영향을 미치는 유일한 요소는 아니다. 파울리 반발, 캐리어 농도 기울기, 전자기 유도 및 열 효과도 중요한 역할을 한다.

전자 회로에서 측정되는 '전압'은 전자의 화학퍼텐셜(페르미 준위)과 관련이 있다. 전압계의 리드를 회로의 두 점에 연결하면 표시되는 전압은 단위 전하가 한 점에서 다른 점으로 이동할 때 전달되는 총 일의 척도이다. 서로 다른 전압의 두 점 사이에 단순한 와이어를 연결하면(단락 회로) 전류가 양의 전압에서 음의 전압으로 흘러 사용 가능한 일을 열로 변환한다.

물체의 페르미 준위는 전자를 추가하는 데 필요한 일, 또는 전자를 제거하여 얻는 일을 나타낸다. 따라서 전자 회로의 두 점 ''A''와 ''B'' 사이에서 관찰되는 전압 차이 ''V''A − ''V''B는 페르미 준위에서 해당 화학퍼텐셜 차이 ''μ''A − ''μ''B와 다음 공식으로 정확하게 관련된다.[5]

: ''V''A - ''V''B = (''μ''A - ''μ''B)/(-''e'')

여기서 −''e''는 전자 전하이다.

전자는 높은 ''μ''(낮은 전압)의 물체에서 낮은 ''μ''(높은 전압)으로 이동한다. 이 전자 흐름은 낮은 ''μ''를 증가시키고 높은 ''μ''를 감소시킨다. 결국 ''μ''는 두 물체 모두에서 동일한 값으로 안정된다. 이는 전자 회로의 평형(꺼짐) 상태에 대한 중요한 사실로 이어진다.

: ''열역학적 평형 상태의 전자 회로는 연결된 부분 전체에 걸쳐 일정한 페르미 준위를 갖는다.''[6]

이는 평형 상태에서 두 점 사이의 전압(전압계로 측정)이 0이 됨을 의미한다. 여기서 열역학적 평형은 회로가 내부적으로 연결되어 있고 배터리 또는 기타 전원을 포함하지 않거나 온도 변화가 없음을 요구한다.

3. 고체의 띠 구조와 페르미 준위



전류는 보통 정전기적 전위(갈바니 전위) 차이에 의해 발생한다고 알려져 있지만, 이는 정확하지 않다.[3] pn 접합과 같이 여러 재료로 만들어진 소자는 평형 상태에서 내부 정전기적 전위차를 갖지만, 순 전류는 발생하지 않는다. 전압계를 접합부에 연결하면 0볼트가 측정된다.[4] 이는 정전기적 전위 외에도 파울리 반발, 캐리어 농도 기울기, 전자기 유도, 열 효과 등이 전류 흐름에 영향을 미치기 때문이다.

실제로 전자 회로에서 측정되는 '전압'은 전자의 화학퍼텐셜(페르미 준위)과 관련이 있다. 전압계를 회로의 두 점에 연결하면, 단위 전하가 한 점에서 다른 점으로 이동할 때 전달되는 총 일의 양을 측정할 수 있다. 서로 다른 전압의 두 점 사이에 전선을 연결하면 전류가 양의 전압에서 음의 전압으로 흘러, 사용 가능한 에너지가 열로 변환된다.

물체의 페르미 준위는 전자를 추가하거나 제거할 때 필요한 에너지를 나타낸다. 따라서 전자 회로의 두 점 ''A''와 ''B'' 사이의 전압 차이 ''V''A − ''V''B는 페르미 준위에서의 화학퍼텐셜 차이 ''μ''A − ''μ''B와 다음과 같이 관련된다.[5]

: V_\mathrm{A} - V_\mathrm{B} = \frac{\mu_\mathrm{A} - \mu_\mathrm{B}}{-e}

여기서 −''e''는 전자 전하이다.

전자가 높은 ''μ''(낮은 전압)에서 낮은 ''μ''(높은 전압)으로 이동하면, 전하 또는 다른 반발 효과로 인해 낮은 ''μ''는 증가하고 높은 ''μ''는 감소한다. 결국 ''μ''는 두 물체에서 동일한 값으로 안정된다. 이는 전자 회로의 평형 상태(꺼짐)에 대한 중요한 사실이며, 열역학적 평형 상태의 전자 회로는 연결된 부분 전체에 걸쳐 일정한 페르미 준위를 갖는다는 것을 의미한다.[6]

이는 또한 평형 상태에서 두 점 사이의 전압(전압계로 측정)이 0이 됨을 의미한다. 여기서 열역학적 평형은 회로가 내부적으로 연결되어 있고 배터리나 기타 전원이 없으며, 온도 변화가 없는 상태를 말한다.

고체의 띠 이론에서 전자는 각각 ϵ으로 표시되는 단일 입자 에너지 고유 상태로 구성된 일련의 띠를 차지한다. 이와 관련된 내용은 하위 섹션을 참조한다.

3. 1. 페르미-디랙 분포



고체의 띠 이론에서 전자는 ϵ으로 표시되는 단일 입자 에너지 고유 상태로 구성된 일련의 띠를 차지한다. 이 단일 입자 그림은 근사치이지만 전자 거동에 대한 이해를 크게 단순화하며 일반적으로 올바르게 적용될 때 정확한 결과를 제공한다.

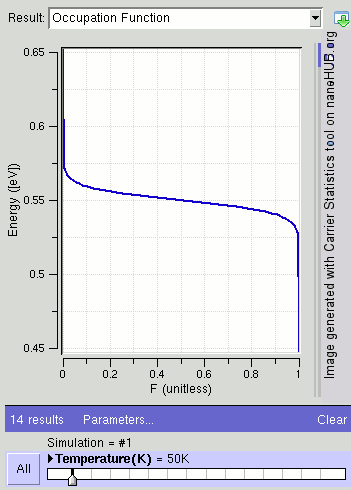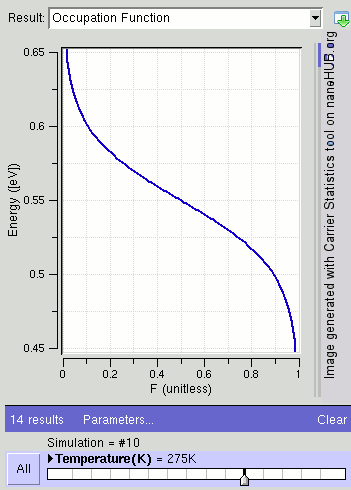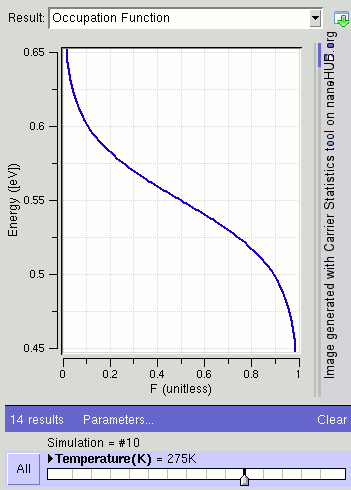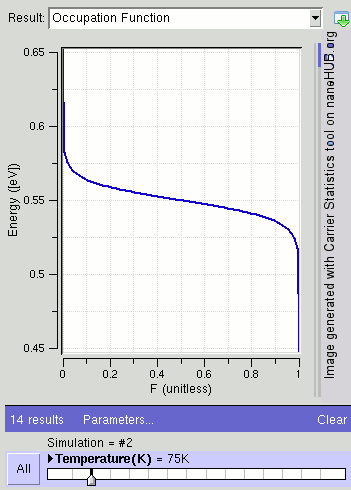
페르미-디랙 분포 f(\epsilon)는 에너지 ϵ을 갖는 상태가 전자에 의해 점유될 확률을 (열역학적 평형에서) 제공한다.[7]

: f(\epsilon) = \frac{1}{e^{(\epsilon - \mu)/k_\mathrm{B} T} + 1}

여기서 ''T''는 절대 온도이고, ''k''B는 볼츠만 상수이다. 페르미 준위(ϵ = μ)에 상태가 있는 경우 이 상태는 50%의 확률로 점유될 것이다. 이 분포는 왼쪽 그림에 표시되어 있다. ''f''가 1에 가까울수록 이 상태가 점유될 확률이 높아진다. ''f''가 0에 가까울수록 이 상태가 비어 있을 확률이 높아진다.

μ의 위치는 재료의 띠 구조 내에서 재료의 전기적 거동을 결정하는 데 중요하다.

  • 절연체에서 μ는 전류를 전달할 수 있는 상태에서 멀리 떨어진 큰 밴드갭 내에 있다.
  • 금속, 반금속 또는 축퇴 반도체에서 μ는 비편재화된 띠 내에 있다. μ 근처의 많은 상태가 열적으로 활성화되어 전류를 쉽게 전달한다.
  • 본질적인 반도체 또는 약하게 도핑된 반도체에서 μ는 띠 가장자리에 충분히 가까워 해당 띠 가장자리 근처에 열적으로 여기된 캐리어가 소량 존재한다.


반도체와 반금속에서 띠 구조에 대한 μ의 위치는 일반적으로 도핑이나 게이팅을 통해 상당한 정도로 제어할 수 있다. 이러한 제어는 전극에 의해 고정되는 μ를 변경하지 않고 오히려 전체 띠 구조가 위아래로 이동하도록 한다(때로는 띠 구조의 모양도 변경됨). 반도체의 페르미 준위에 대한 자세한 내용은 (예를 들어) Sze를 참조하십시오.[8]

3. 2. 띠 구조와 재료의 특성



고체의 띠 이론에서 전자는 각각 ϵ으로 표시되는 단일 입자 에너지 고유 상태로 구성된 일련의 띠를 차지한다. 이 단일 입자 그림은 근사치이지만 전자 거동에 대한 이해를 크게 단순화하며 일반적으로 올바르게 적용될 때 정확한 결과를 제공한다.

페르미-디랙 분포 f(\epsilon)는 열역학적 평형에서 에너지 ϵ을 갖는 상태가 전자에 의해 점유될 확률을 제공한다.[7]

: f(\epsilon) = \frac{1}{e^{(\epsilon - \mu)/k_\mathrm{B} T} + 1}

여기서 ''T''는 절대 온도이고 ''k''B는 볼츠만 상수이다. 페르미 준위(ϵ = μ)에 상태가 있는 경우 이 상태는 50%의 확률로 점유될 것이다. 이 분포는 왼쪽 그림에 표시되어 있다. ''f''가 1에 가까울수록 이 상태가 점유될 확률이 높아진다. ''f''가 0에 가까울수록 이 상태가 비어 있을 확률이 높아진다.

μ의 위치는 재료의 띠 구조 내에서 재료의 전기적 거동을 결정하는 데 중요하다.

  • 절연체에서 μ는 전류를 전달할 수 있는 상태에서 멀리 떨어진 큰 밴드갭 내에 있다.
  • 금속, 반금속 또는 축퇴 반도체에서 μ는 비편재화된 띠 내에 있다. μ 근처의 많은 상태가 열적으로 활성화되어 전류를 쉽게 전달한다.
  • 본질적인 반도체 또는 약하게 도핑된 반도체에서 μ는 띠 가장자리에 충분히 가까워 해당 띠 가장자리 근처에 열적으로 여기된 캐리어가 소량 존재한다.


반도체와 반금속에서 띠 구조에 대한 μ의 위치는 일반적으로 도핑이나 게이팅을 통해 상당한 정도로 제어할 수 있다. 이러한 제어는 전극에 의해 고정되는 μ를 변경하지 않고 오히려 전체 띠 구조가 위아래로 이동하도록 한다(때로는 띠 구조의 모양도 변경됨). 반도체의 페르미 준위에 대한 자세한 내용은 Sze를 참조하라.[8]

3. 3. 국소 전도띠 기준 페르미 준위 (ζ)

만약 기호 ''ℰ''가 밴드를 둘러싸는 밴드 가장자리 에너지 ''ϵ''C를 기준으로 측정된 전자 에너지 준위를 나타내는 데 사용된다면, 일반적으로 다음과 같은 관계가 성립한다.

: \text{ℰ} = \varepsilon - \varepsilon_{\rm C}.

밴드 가장자리에 대한 페르미 준위를 참조하는 매개변수 ''ζ''는 다음과 같이 정의할 수 있다.[9]

: \zeta = \mu - \epsilon_{\rm C}.

따라서 페르미-디랙 분포 함수는 다음과 같이 쓸 수 있다.

: f(\mathcal{E}) = \frac{1}{e^{(\mathcal{E} - \zeta)/k_\mathrm{B} T} + 1}.

금속의 띠 이론은 1927년부터 기초적인 열역학과 통계 역학에 많은 관심을 기울인 좀머펠트에 의해 처음 개발되었다. 혼란스럽게도, 어떤 경우에는 밴드를 기준으로 한 값 ''ζ''가 ''페르미 준위'', ''화학 퍼텐셜'', 또는 ''전기화학 퍼텐셜''로 불릴 수 있으며, 이는 전역적으로 참조되는 페르미 준위와 모호성을 야기한다. 이 문서에서는 ''전도띠 기준 페르미 준위'' 또는 ''내부 화학 퍼텐셜''이라는 용어를 ''ζ''를 가리키는 데 사용한다.

GaAs/AlGaAs 이종접합 기반 고전자 이동도 트랜지스터의 띠 다이어그램에서 전도띠 가장자리 ''E''C의 변화 예시.


''ζ''는 활성 전하 캐리어의 수뿐만 아니라 일반적인 운동 에너지와 직접적으로 관련이 있으며, 따라서 재료의 국소적 특성(예: 전기 전도도)을 결정하는 데 직접적으로 관여한다. 이러한 이유로 단일하고 균질한 전도성 물질 내 전자의 특성에 집중할 때 ''ζ''의 값에 초점을 맞추는 것이 일반적이다. 자유 전자의 에너지 상태와 유추하여, 상태의 ''ℰ''는 그 상태의 운동 에너지이고 ''ϵ''C는 그 퍼텐셜 에너지이다. 이를 고려하여 매개변수 ''ζ''는 ''페르미 운동 에너지''라고도 할 수 있다.

''μ''와 달리, 매개변수 ''ζ''는 평형 상태에서 상수가 아니고, 오히려 재료의 품질과 불순물/도펀트와 같은 요인에 의해 결정되는 ''ϵ''C의 변화로 인해 재료 내 위치에 따라 변한다. 반도체 또는 반금속의 표면 근처에서 ''ζ''는 전계 효과 트랜지스터에서와 같이 외부에서 인가되는 전기장에 의해 강하게 제어될 수 있다. 다중 밴드 재료에서 ''ζ''는 단일 위치에서 여러 값을 가질 수도 있다. 예를 들어, 알루미늄 조각에는 페르미 준위를 교차하는 두 개의 전도 띠가 있다(다른 재료에는 더 많은 띠가 있음).[10] 각 띠는 서로 다른 가장자리 에너지 ''ϵ''C와 서로 다른 ''ζ''를 갖는다.

절대 영도에서의 ''ζ''의 값은 종종 ''ζ''0로 표기되는 페르미 에너지로 널리 알려져 있다. 혼란스럽게도, ''페르미 에너지''라는 이름은 때때로 영도가 아닌 온도에서의 ''ζ''를 가리키는 데 사용된다.

4. 비평형 상태에서의 페르미 준위

전류는 정전기적 전위 차이에 의해 발생한다는 말이 있지만, 이는 정확하지 않다.[3] pn 접합과 같이 여러 재료로 만들어진 소자는 평형 상태에서 내부 정전기적 전위차를 가지지만, 순 전류는 흐르지 않는다. 전압계를 접합부에 연결하면 0볼트를 측정한다.[4] 이는 정전기적 전위 외에도 파울리 반발, 캐리어 농도 기울기, 전자기 유도, 열 효과 등이 전하 흐름에 영향을 미치기 때문이다.

전자 회로에서 측정되는 "전압"은 전자의 화학퍼텐셜(페르미 준위)과 관련이 있다. 전압계로 회로의 두 점 사이의 전압을 측정하면, 단위 전하가 한 점에서 다른 점으로 이동할 때 전달되는 총 일의 양을 알 수 있다. 서로 다른 전압의 두 점을 전선으로 연결하면(단락 회로), 전류는 양의 전압에서 음의 전압으로 흘러 일을 열로 변환한다.

물체의 페르미 준위는 전자를 추가하는 데 필요한 일, 또는 전자를 제거하여 얻는 일을 나타낸다. 따라서 전자 회로의 두 점 ''A''와 ''B'' 사이의 전압 차이 ''V''A − ''V''B는 페르미 준위에서의 화학퍼텐셜 차이 ''μ''A − ''μ''B와 다음 공식으로 정확하게 관련된다.[5]

: V_\mathrm{A} - V_\mathrm{B} = \frac{\mu_\mathrm{A} - \mu_\mathrm{B}}{-e}

여기서 −''e''는 전자 전하이다.

전자는 높은 ''μ''(낮은 전압)에서 낮은 ''μ''(높은 전압)으로 이동한다. 이 전자 흐름은 낮은 ''μ''를 증가시키고 높은 ''μ''를 감소시켜 결국 두 물체의 ''μ'' 값을 같게 만든다. 이는 전자 회로의 평형(꺼짐) 상태에 대한 중요한 사실이다.

즉, 평형 상태에서 두 점 사이의 전압은 0이 된다. 열역학적 평형은 회로가 내부적으로 연결되어 있고, 배터리나 전원이 없으며, 온도 변화가 없는 상태를 의미한다.

열역학적 평형 상태의 고체 소자에서 페르미 준위(μ)와 온도(T)는 잘 정의된 상수이다. 하지만 소자가 평형 상태를 벗어나면 페르미 준위와 온도는 더 이상 잘 정의되지 않는다. 이 경우, 특정 위치의 상태 점유를 열적 분포로 설명하는 준페르미 준위와 준온도를 정의할 수 있다. 이러한 설명이 가능하면 소자는 준평형 상태에 있다고 한다.

준평형 접근 방식을 통해 금속의 전기 전도도(μ의 기울기)나 열전도도(T의 기울기)와 같은 비평형 효과를 설명할 수 있다. 준-μ와 준-T는 다음과 같은 비평형 상황에서 달라지거나 존재하지 않을 수 있다.


  • 시스템에 화학적 불균형이 있는 경우 (전지)
  • 시스템이 변화하는 전자기장에 노출된 경우 (축전기, 인덕터, 변압기)
  • 태양과 같은 다른 온도의 광원으로부터 조명을 받는 경우 (태양 전지)
  • 소자 내부의 온도가 일정하지 않은 경우 (열전대)
  • 소자가 변경되었지만 재평형화될 시간이 충분하지 않은 경우 (압전기, 초전기)


고에너지 레이저 펄스를 받은 직후와 같이 전자 분포를 열적 분포로 설명할 수 없는 경우, 준페르미 준위나 준온도를 정의할 수 없다. 이 경우 전자는 비열화되었다고 한다. 태양 전지가 일정하게 조명을 받는 경우와 같이 덜 극적인 상황에서는 준평형 설명이 가능하지만, 서로 다른 띠(전도대, 전자대)에 대해 별도의 μ와 T 값을 할당해야 할 수 있다. 전류가 흐를 때 μ와 T 값은 재료 계면(pn 접합)에서 불연속적으로 점프할 수 있으며, 계면 자체에서는 잘 정의되지 않을 수 있다.

5. 관련 용어



전류는 정전기적 전위(갈바니 전위)의 차이에 의해 발생한다고 말해지지만, 이는 정확히 사실이 아니다.[3] 반례로, pn 접합과 같은 다중 재료 소자는 평형 상태에서 내부 정전기적 전위차를 포함하지만, 동반되는 순 전류는 없다. 전압계를 접합부에 연결하면 단순히 0볼트를 측정한다.[4] 명확히, 정전기적 전위는 물질 내 전하 흐름에 영향을 미치는 유일한 요소가 아니다. 파울리 반발, 캐리어 농도 기울기, 전자기 유도 및 열 효과도 중요한 역할을 한다.

사실, 전자 회로에서 측정되는 '전압'이라는 양은 전자의 화학퍼텐셜(페르미 준위)과 간단한 관계를 갖는다. 전압계의 리드를 회로의 두 점에 연결하면 표시된 전압은 단위 전하가 한 점에서 다른 점으로 이동할 때 전달되는 '총' 일의 척도이다. 서로 다른 전압의 두 점(단락 회로 형성) 사이에 단순한 와이어를 연결하면 전류가 양의 전압에서 음의 전압으로 흘러 사용 가능한 일을 열로 변환한다.

물체의 페르미 준위는 전자를 추가하는 데 필요한 일 또는 전자를 제거하여 얻는 일을 나타낸다. 따라서 전자 회로의 두 점 ''A''와 ''B'' 사이에서 관찰되는 전압 차이 ''V''A − ''V''B는 페르미 준위에서 해당 화학퍼텐셜 차이 ''μ''A − ''μ''B와 다음 공식으로 정확하게 관련된다.[5]

: ''V''A - ''V''B = (''μ''A - ''μ''B) / -''e''

여기서 −''e''는 전자 전하이다.

위 논의에서 알 수 있듯이, 단순한 경로가 제공되면 전자는 높은 ''μ''(낮은 전압)의 물체에서 낮은 ''μ''(높은 전압)으로 이동한다. 이 전자 흐름은 하전 또는 다른 반발 효과로 인해 낮은 ''μ''가 증가하고 마찬가지로 높은 ''μ''가 감소하게 한다. 결국 ''μ''는 두 물체 모두에서 동일한 값으로 안정된다. 이는 전자 회로의 평형(꺼짐) 상태에 대한 중요한 사실로 이어진다.

:: ''열역학적 평형 상태의 전자 회로는 연결된 부분 전체에 걸쳐 일정한 페르미 준위를 갖는다.''[6]

이는 또한 평형 상태에서 두 점 사이의 전압(전압계로 측정)이 0이 됨을 의미한다. 여기서 열역학적 평형은 회로가 내부적으로 연결되어 있고 배터리 또는 기타 전원을 포함하지 않거나 온도 변화가 없음을 요구한다.

6. 기술적 세부 사항

전류는 갈바니 전위 차이에 의해 발생한다고 알려져 있지만, 항상 그런 것은 아니다.[3] pn 접합처럼 여러 재료로 만들어진 소자는 평형 상태에서 내부적인 정전기적 전위차를 가지지만, 순 전류는 흐르지 않는다. 전압계로 측정하면 0볼트가 측정된다.[4] 이는 정전기적 전위 외에도 파울리 반발, 캐리어 농도 기울기, 전자기 유도, 열 효과 등 다른 요인들이 전하 흐름에 영향을 미치기 때문이다.

전자 회로에서 측정되는 '전압'은 전자의 화학 퍼텐셜(페르미 준위)과 관련이 있다. 전압계를 회로의 두 점에 연결하면, 표시되는 전압은 단위 전하가 한 점에서 다른 점으로 이동할 때 전달되는 총 일의 양을 나타낸다. 서로 다른 전압의 두 점을 전선으로 연결하면, 전류는 양의 전압에서 음의 전압으로 흐르며 에너지를 열로 변환한다.

물체의 페르미 준위는 전자를 추가하거나 제거할 때 필요한 에너지를 의미한다. 전자 회로의 두 점 A와 B 사이의 전압 차이 ''V''A − ''V''B는 페르미 준위에서의 화학 퍼텐셜 차이 ''μ''A − ''μ''B와 다음 공식으로 정확하게 관련된다.[5]

: V_\mathrm{A} - V_\mathrm{B} = \frac{\mu_\mathrm{A} - \mu_\mathrm{B}}{-e}

여기서 −''e''는 전자 전하이다.

전자는 높은 ''μ''(낮은 전압)에서 낮은 ''μ''(높은 전압)으로 이동한다. 이 이동으로 인해 낮은 ''μ''는 증가하고 높은 ''μ''는 감소하여 결국 두 물체의 ''μ''는 같아진다. 이는 평형 상태에서 두 점 사이의 전압이 0이 됨을 의미한다. 열역학적 평형은 회로가 내부적으로 연결되어 있고, 배터리나 전원이 없으며, 온도 변화가 없는 상태를 말한다.

밴드 가장자리 에너지 ''ϵ''C를 기준으로 측정된 전자 에너지 준위를 ''ℰ''로 나타내면,

: \text{ℰ} = \varepsilon - \varepsilon_{\rm C}.

이다.

밴드 가장자리에 대한 페르미 준위를 나타내는 매개변수 ''ζ''는 다음과 같이 정의된다.[9]

: \zeta = \mu - \epsilon_{\rm C}.

따라서 페르미-디랙 분포 함수는 다음과 같이 쓸 수 있다.

: f(\mathcal{E}) = \frac{1}{e^{(\mathcal{E} - \zeta)/k_\mathrm{B} T} + 1}.

금속의 띠 이론은 좀머펠트가 개발했다. 밴드 기준 값 ''ζ''가 ''페르미 준위'', ''화학 퍼텐셜'', ''전기화학 퍼텐셜'' 등으로 불려, 전역 참조 페르미 준위와 혼동을 일으킬 수 있다. 이 문서에서는 ''ζ''를 ''전도띠 기준 페르미 준위'' 또는 ''내부 화학 퍼텐셜''이라고 부른다.

''ζ''는 활성 전하 캐리어 수, 운동 에너지와 관련되어 재료의 국소적 특성(예: 전기 전도도)을 결정한다. 따라서 단일하고 균질한 전도성 물질 내 전자의 특성에 집중할 때 ''ζ'' 값에 초점을 맞춘다. 자유 전자의 에너지 상태와 유추하여, ''ℰ''는 운동 에너지, ''ϵ''C는 퍼텐셜 에너지이다. ''ζ''는 ''페르미 운동 에너지''라고도 할 수 있다.

''μ''와 달리 ''ζ''는 평형 상태에서 상수가 아니고, 재료의 품질, 불순물 등에 의해 결정되는 ''ϵ''C 변화로 인해 위치에 따라 변한다. 반도체나 반금속 표면 근처에서 ''ζ''는 외부 전기장에 의해 강하게 제어될 수 있다(전계 효과 트랜지스터). 다중 밴드 재료에서 ''ζ''는 한 위치에서 여러 값을 가질 수 있다. 예를 들어 알루미늄은 페르미 준위를 교차하는 두 개의 전도 띠를 가진다.[10]

절대 영도에서 ''ζ'' 값은 페르미 에너지(''ζ''0)로 알려져 있다. 그러나 ''페르미 에너지''라는 이름은 때때로 영도가 아닌 온도에서의 ''ζ''를 가리키기도 한다.

고체의 띠 이론에서 전자는 ϵ으로 표시되는 에너지 고유 상태를 가지는 띠들을 채운다. 이 단일 입자 그림은 근사적이지만, 전자 거동을 이해하는데 도움을 주며, 올바르게 적용하면 정확한 결과를 제공한다.

페르미-디랙 분포 f(\epsilon)는 열역학적 평형에서 에너지 ϵ을 갖는 상태가 전자에 의해 점유될 확률을 나타낸다.[7]

: f(\epsilon) = \frac{1}{e^{(\epsilon - \mu)/k_\mathrm{B} T} + 1}

여기서 ''T''는 절대 온도이고, ''k''B는 볼츠만 상수이다. 페르미 준위(ϵ = μ)에 상태가 존재하면, 이 상태는 50%의 확률로 전자가 채워진다. ''f''가 1에 가까울수록 전자가 상태를 점유할 확률이 높고, ''f''가 0에 가까울수록 상태가 비어 있을 확률이 높다.

μ (페르미 준위)의 위치는 재료의 띠 구조 내에서 전기적 거동을 결정하는 데 중요한 역할을 한다.


  • 절연체에서 μ는 전류를 전달할 수 있는 상태와 멀리 떨어진 큰 띠틈 내에 위치한다.
  • 금속, 반금속 또는 축퇴 반도체에서 μ는 비편재화된 띠 내에 존재한다. μ 근처의 많은 상태는 열적으로 활성화되어 전류를 쉽게 전달한다.
  • 본질적인 반도체 또는 약하게 도핑된 반도체에서 μ는 띠 가장자리에 충분히 가까워, 해당 띠 가장자리 근처에 열적으로 여기된 운반자가 소량 존재한다.


반도체와 반금속에서 띠 구조에 대한 μ의 위치는 도핑이나 게이팅을 통해 조절할 수 있다. 이러한 조절은 전극에 의해 고정되는 μ를 바꾸는 것이 아니라, 전체 띠 구조를 위아래로 이동시킨다(때로는 띠 구조의 모양도 변화시킨다).[8]

단일 전자에 의한 "충전 효과"가 무시할 수 없을 정도로 큰 경우, 위 정의를 명확히 해야 한다. 예를 들어, 두 개의 평행판으로 만들어진 축전기에서 축전기가 충전되지 않은 경우, 페르미 준위는 양쪽에서 동일하여 전자를 이동하는 데 에너지가 필요하지 않다고 생각할 수 있다. 그러나 전자가 이동하면 축전기가 약간 충전되어 약간의 에너지가 필요하다. 일반적인 축전기에서는 무시할 만하지만, 나노 크기 축전기에서는 중요할 수 있다.

화학 포텐셜의 열역학적 정의와 장치의 상태(전기적 절연 여부, 전극 연결 여부)에 대해 정확해야 한다.

  • 물체가 전극과 전자 및 에너지를 교환할 수 있는 경우 (그랜드 정준 앙상블), 화학 포텐셜 μ는 전극에 의해 고정되고, 물체의 전자 수 N는 변동 가능하다. 화학 포텐셜은 전자의 ''평균'' 수를 미소량만큼 증가시키는 데 필요한 미소량의 일이다.
  • 물체의 전자 수가 고정된 경우(정준 앙상블), "화학 포텐셜"은 이미 정확히 N개의 전자를 가진 물체에 전자 하나를 추가하는 데 필요한 일로 정의된다.[13]


이러한 화학 포텐셜은 열역학적 극한을 제외하고는 동일하지 않다. 이 차이는 쿨롱 차단을 보이는 작은 시스템에서 중요하다.[14] μ (전자 수가 변동될 수 있는 경우)는 작은 시스템에서도 볼트미터 전압과 관련된다. 페르미 준위는 하나의 전하량에 의한 결정적 충전 사건이 아니라, 전자의 미소량에 의한 통계적 충전 사건에 의해 정의된다.

6. 1. 용어 문제

전류는 갈바니 전위의 차이에 의해 발생한다고 알려져 있지만, 항상 그런 것은 아니다.[3] pn 접합처럼 여러 재료로 만들어진 소자는 평형 상태에서 내부적인 정전기적 전위차를 가지지만, 순 전류는 흐르지 않는다. 전압계로 측정하면 0볼트가 측정된다.[4] 이는 정전기적 전위 외에도 파울리 반발, 캐리어 농도 기울기, 전자기 유도, 열 효과 등 다른 요인들이 전하 흐름에 영향을 미치기 때문이다.

전자 회로에서 측정되는 '전압'은 전자의 화학 퍼텐셜(페르미 준위)과 관련이 있다. 전압계를 회로의 두 점에 연결하면, 표시되는 전압은 단위 전하가 한 점에서 다른 점으로 이동할 때 전달되는 총 일의 양을 나타낸다. 서로 다른 전압의 두 점을 전선으로 연결하면, 전류는 양의 전압에서 음의 전압으로 흐르며 에너지를 열로 변환한다.

물체의 페르미 준위는 전자를 추가하거나 제거할 때 필요한 에너지를 의미한다. 전자 회로의 두 점 A와 B 사이의 전압 차이 ''V''A − ''V''B는 페르미 준위에서의 화학 퍼텐셜 차이 ''μ''A − ''μ''B와 다음 공식으로 정확하게 관련된다.[5]

: V_\mathrm{A} - V_\mathrm{B} = \frac{\mu_\mathrm{A} - \mu_\mathrm{B}}{-e}

여기서 −''e''는 전자 전하이다.

전자는 높은 ''μ''(낮은 전압)에서 낮은 ''μ''(높은 전압)으로 이동한다. 이 이동으로 인해 낮은 ''μ''는 증가하고 높은 ''μ''는 감소하여 결국 두 물체의 ''μ''는 같아진다. 이는 전자 회로의 평형 상태에 대한 중요한 사실이다. 이는 평형 상태에서 두 점 사이의 전압이 0이 됨을 의미한다. 열역학적 평형은 회로가 내부적으로 연결되어 있고, 배터리나 전원이 없으며, 온도 변화가 없는 상태를 말한다.

밴드 가장자리 에너지 ''ϵ''C를 기준으로 측정된 전자 에너지 준위를 ''ℰ''로 나타내면,

: \text{ℰ} = \varepsilon - \varepsilon_{\rm C}.

이다.

밴드 가장자리에 대한 페르미 준위를 나타내는 매개변수 ''ζ''는 다음과 같이 정의된다.[9]

: \zeta = \mu - \epsilon_{\rm C}.

따라서 페르미-디랙 분포 함수는 다음과 같이 쓸 수 있다.

: f(\mathcal{E}) = \frac{1}{e^{(\mathcal{E} - \zeta)/k_\mathrm{B} T} + 1}.

금속의 띠 이론은 좀머펠트가 개발했다. 혼란스럽게도, 밴드 기준 값 ''ζ''가 ''페르미 준위'', ''화학 퍼텐셜'', ''전기화학 퍼텐셜'' 등으로 불려, 전역 참조 페르미 준위와 혼동을 일으킬 수 있다. 이 문서에서는 ''ζ''를 ''전도띠 기준 페르미 준위'' 또는 ''내부 화학 퍼텐셜''이라고 부른다.

''ζ''는 활성 전하 캐리어 수, 운동 에너지와 관련되어 재료의 국소적 특성(예: 전기 전도도)을 결정한다. 따라서 단일하고 균질한 전도성 물질 내 전자의 특성에 집중할 때 ''ζ'' 값에 초점을 맞춘다. 자유 전자의 에너지 상태와 유추하여, ''ℰ''는 운동 에너지, ''ϵ''C는 퍼텐셜 에너지이다. ''ζ''는 ''페르미 운동 에너지''라고도 할 수 있다.

''μ''와 달리 ''ζ''는 평형 상태에서 상수가 아니고, 재료의 품질, 불순물 등에 의해 결정되는 ''ϵ''C 변화로 인해 위치에 따라 변한다. 반도체나 반금속 표면 근처에서 ''ζ''는 외부 전기장에 의해 강하게 제어될 수 있다(전계 효과 트랜지스터). 다중 밴드 재료에서 ''ζ''는 한 위치에서 여러 값을 가질 수 있다. 예를 들어 알루미늄은 페르미 준위를 교차하는 두 개의 전도 띠를 가진다.[10]

절대 영도에서 ''ζ'' 값은 페르미 에너지(''ζ''0)로 알려져 있다. 그러나 ''페르미 에너지''라는 이름은 때때로 영도가 아닌 온도에서의 ''ζ''를 가리키기도 한다.

"페르미 준위"는 주로 반도체 내 전자의 고체 물리학에서 사용되며, 서로 다른 도핑 수준을 가진 재료로 구성된 소자의 띠 그림을 설명하는 데 필요하다. 하지만 "띠 기준 페르미 준위" (''ζ'')를 "페르미 준위"라고 부정확하게 사용하는 경우도 있다. 과학자와 엔지니어들이 도핑이나 전계 효과로 인한 ''ϵ''C 변화를 설명하며 페르미 준위를 "제어", "고정", "조정"한다고 말하는 경우가 있지만, 열역학적 평형에서 도체의 페르미 준위는 항상 전극의 페르미 준위와 같게 고정되어 있으며, 바뀌는 것은 띠 구조이다.

비슷한 모호성은 "화학 퍼텐셜"과 "전기화학적 퍼텐셜" 용어 사이에도 존재한다. 페르미 ''준위''와 페르미 ''에너지''는 반드시 같은 것이 아니다. 양자 역학에서 페르미 에너지는 "이상적인 비상호작용, 무질서가 없고, 절대 영도의 페르미 기체에서 페르미온의 최대 운동 에너지"를 가리킨다. 이 개념은 이론적이지만, 백색왜성, 중성자별, 원자핵, 금속 내 전자를 근사적으로 설명하는 데 사용된다. 반면, 반도체 물리학 및 공학 분야에서 "페르미 에너지"는 종종 이 문서에서 설명하는 페르미 준위를 가리킨다.[11]

6. 2. 페르미 에너지와의 관계



고체의 띠 이론에서 전자는 ϵ으로 표시되는 에너지 고유 상태를 가지는 띠들을 채운다. 이 단일 입자 그림은 근사적이지만, 전자 거동을 이해하는데 도움을 주며, 올바르게 적용하면 정확한 결과를 제공한다.

페르미-디랙 분포 f(\epsilon)는 열역학적 평형에서 에너지 ϵ을 갖는 상태가 전자에 의해 점유될 확률을 나타낸다.[7]

: f(\epsilon) = \frac{1}{e^{(\epsilon - \mu)/k_\mathrm{B} T} + 1}

여기서 ''T''는 절대 온도이고, ''k''B는 볼츠만 상수이다. 페르미 준위(ϵ = μ)에 상태가 존재하면, 이 상태는 50%의 확률로 전자가 채워진다. 이 분포는 왼쪽 그림에 나타나 있다. ''f''가 1에 가까울수록 전자가 상태를 점유할 확률이 높고, ''f''가 0에 가까울수록 상태가 비어 있을 확률이 높다.

μ (페르미 준위)의 위치는 재료의 띠 구조 내에서 전기적 거동을 결정하는 데 중요한 역할을 한다.

  • 절연체에서 μ는 전류를 전달할 수 있는 상태와 멀리 떨어진 큰 띠틈 내에 위치한다.
  • 금속, 반금속 또는 축퇴 반도체에서 μ는 비편재화된 띠 내에 존재한다. μ 근처의 많은 상태는 열적으로 활성화되어 전류를 쉽게 전달한다.
  • 본질적인 반도체 또는 약하게 도핑된 반도체에서 μ는 띠 가장자리에 충분히 가까워, 해당 띠 가장자리 근처에 열적으로 여기된 운반자가 소량 존재한다.


반도체와 반금속에서 띠 구조에 대한 μ의 위치는 도핑이나 게이팅을 통해 조절할 수 있다. 이러한 조절은 전극에 의해 고정되는 μ를 바꾸는 것이 아니라, 전체 띠 구조를 위아래로 이동시킨다(때로는 띠 구조의 모양도 변화시킨다).[8]

6. 3. 페르미 준위 기준점

전류는 정전기적 전위 차이로 발생한다고 알려져 있지만, 항상 그런 것은 아니다.[3] 예를 들어, pn 접합과 같이 여러 재료로 만들어진 소자는 평형 상태에서 내부 정전기적 전위차를 가지지만, 순 전류는 흐르지 않는다. 이 접합부에 전압계를 연결하면 0볼트가 측정된다.[4] 이는 정전기적 전위 외에도 파울리 반발, 캐리어 농도 기울기, 전자기 유도, 열 효과 등 다른 요인들이 전하 흐름에 영향을 미치기 때문이다.

전압계로 측정되는 '전압'은 전자의 화학퍼텐셜(페르미 준위)과 관련이 있다. 전압계의 리드를 회로의 두 지점에 연결하면, 표시되는 전압은 단위 전하가 한 지점에서 다른 지점으로 이동할 때 전달되는 총 일의 양을 나타낸다. 서로 다른 전압을 가진 두 지점 사이에 전선을 연결하면, 전류는 양의 전압에서 음의 전압으로 흘러 일을 열로 변환한다.

물체의 페르미 준위는 전자를 추가하거나 제거할 때 필요한 에너지를 나타낸다. 따라서 전자 회로의 두 지점 ''A''와 ''B'' 사이의 전압 차이 ''V''A − ''V''B는 페르미 준위에서의 화학퍼텐셜 차이 ''μ''A − ''μ''B와 다음 공식으로 정확하게 관련된다.[5]

V_\mathrm{A} - V_\mathrm{B} = \frac{\mu_\mathrm{A} - \mu_\mathrm{B}}{-e}

여기서 −''e''는 전자 전하이다.

전자는 높은 ''μ''(낮은 전압)에서 낮은 ''μ''(높은 전압)으로 이동한다. 이 이동으로 인해 낮은 ''μ''는 증가하고 높은 ''μ''는 감소하여 결국 두 물체의 ''μ''는 같아진다. 이는 열역학적 평형 상태의 전자 회로가 연결된 부분 전체에 걸쳐 일정한 페르미 준위를 갖는다는 것을 의미한다.[6] 또한, 평형 상태에서 두 점 사이의 전압은 0이 된다. (열역학적 평형은 회로가 내부적으로 연결되어 있고, 배터리나 전원이 없으며, 온도 변화가 없는 상태를 의미한다.)

에너지의 영점은 좌표계의 원점처럼 임의로 정의할 수 있으며, 관측 가능한 현상은 에너지 차이에만 의존한다. 그러나 서로 다른 물체를 비교할 때는 모든 물체가 에너지 영점의 위치를 일관되게 선택해야 한다.

접지 또는 지구와 같은 크고 물리적인 도체를 공통점으로 선택하는 것이 실용적이다. 이러한 도체는 열역학적 평형 상태에 있고, ''μ''가 잘 정의되어 있으며, 전하 저장소 역할을 하여 충전 효과 없이 전자를 추가하거나 제거할 수 있다. 또한, 전압계로 다른 물체의 페르미 준위를 측정하기 쉽다.

두 금속이 열역학적 평형 상태(페르미 준위 EF가 같음)에 있을 때, 일함수의 차이로 인해 진공 정전 포텐셜 ''ϕ''는 평평하지 않다.


진공 내 정지 전자의 상태를 에너지 기준점으로 사용하는 것은 권장되지 않는다.[12] 진공 내 모든 지점이 동등하지 않기 때문이다. 열역학적 평형 상태에서 진공에는 1V 정도의 전기적 전위차(볼타 전위)가 존재하며, 이는 진공에 노출된 서로 다른 도체 재료 간의 일함수 변화 때문이다. 도체 바로 바깥쪽의 정전 포텐셜은 재료, 표면, 오염 등에 따라 달라진다.

보편성에 가장 근접한 매개변수는 지구 기준 페르미 준위이며, 전압계로 측정할 수 있다는 장점도 있다.

6. 4. 작은 시스템에서의 불연속적인 전하 효과

전류는 정전기적 전위 차이에 의해 발생한다고 알려져 있지만, 항상 그런 것은 아니다.[3] 예를 들어, pn 접합과 같은 다중 재료 소자는 평형 상태에서 내부 정전기적 전위차를 가지지만 순 전류는 흐르지 않는다. 전압계로 측정하면 0볼트가 측정된다.[4] 이는 정전기적 전위 외에도 파울리 반발, 캐리어 농도 기울기, 전자기 유도, 열 효과 등 다른 요인들이 전하 흐름에 영향을 미치기 때문이다.

전자 회로에서 측정되는 '전압'은 전자의 화학퍼텐셜(페르미 준위)과 관련이 있다. 전압계로 회로의 두 점을 측정하면, 표시되는 전압은 단위 전하가 한 점에서 다른 점으로 이동할 때 전달되는 총 일의 척도이다. 서로 다른 전압의 두 점을 전선으로 연결하면(단락 회로), 전류는 양의 전압에서 음의 전압으로 흘러 에너지를 열로 변환한다.

물체의 페르미 준위는 전자를 추가하거나 제거하는 데 필요한 에너지를 나타낸다. 전자 회로의 두 점 ''A''와 ''B'' 사이의 전압 차이 ''V''A − ''V''B는 페르미 준위의 화학퍼텐셜 차이 ''μ''A − ''μ''B와 다음과 같이 관련된다.[5]

: ''V''A - ''V''B = (''μ''A - ''μ''B)/(-''e'')

여기서 -''e''는 전자 전하이다.

전자는 높은 ''μ''(낮은 전압)에서 낮은 ''μ''(높은 전압)으로 이동한다. 이 흐름은 낮은 ''μ''를 증가시키고 높은 ''μ''를 감소시켜 결국 두 물체의 ''μ'' 값을 같게 만든다. 이는 전자 회로의 평형 상태에 대한 중요한 사실로 이어진다.

> 열역학적 평형 상태의 전자 회로는 연결된 부분 전체에 걸쳐 일정한 페르미 준위를 갖는다.[6]

이는 평형 상태에서 두 점 사이의 전압이 0임을 의미한다. 열역학적 평형은 회로가 내부적으로 연결되어 있고, 배터리나 전원이 없으며, 온도 변화가 없는 상태를 말한다.

단일 전자에 의한 "충전 효과"가 무시할 수 없을 정도로 큰 경우, 위 정의를 명확히 해야 한다. 예를 들어, 두 개의 평행판으로 만들어진 축전기에서 축전기가 충전되지 않은 경우, 페르미 준위는 양쪽에서 동일하여 전자를 이동하는 데 에너지가 필요하지 않다고 생각할 수 있다. 그러나 전자가 이동하면 축전기가 약간 충전되어 약간의 에너지가 필요하다. 일반적인 축전기에서는 무시할 만하지만, 나노 크기 축전기에서는 중요할 수 있다.

화학 포텐셜의 열역학적 정의와 장치의 상태(전기적 절연 여부, 전극 연결 여부)에 대해 정확해야 한다.

  • 물체가 전극과 전자 및 에너지를 교환할 수 있는 경우 (그랜드 정준 앙상블), 화학 포텐셜 μ는 전극에 의해 고정되고, 물체의 전자 수 N는 변동 가능하다. 화학 포텐셜은 전자의 ''평균'' 수를 미소량만큼 증가시키는 데 필요한 미소량의 일이다.


::

  • 물체의 전자 수가 고정된 경우(정준 앙상블), "화학 포텐셜"은 이미 정확히 N개의 전자를 가진 물체에 전자 하나를 추가하는 데 필요한 일로 정의된다.[13]


::

::

이러한 화학 포텐셜은 열역학적 극한을 제외하고는 동일하지 않다. 이 차이는 쿨롱 차단을 보이는 작은 시스템에서 중요하다.[14] μ (전자 수가 변동될 수 있는 경우)는 작은 시스템에서도 볼트미터 전압과 관련된다. 페르미 준위는 하나의 전하량에 의한 결정적 충전 사건이 아니라, 전자의 미소량에 의한 통계적 충전 사건에 의해 정의된다.

참조

[1] 서적 Introduction to Solid State Physics Wiley
[2] 웹사이트 Fermi level physics Britannica https://www.britanni[...] 2023-06-03
[3] 학술지 What does a voltmeter measure?
[4] 서적 Fundamentals of Solid-State Electronics https://archive.org/[...] World Scientific
[5] 서적 Quantum Transport: Atom to Transistor Cambridge University Press
[6] 학술지 Potentially Confusing: Potentials in Electrochemistry
[7] 서적 Thermal Physics https://books.google[...] W. H. Freeman 1980-01-15
[8] 서적 Physics of Semiconductor Devices https://archive.org/[...] Wiley
[9] 서적 Thermodynamics and Statistical Mechanics Academic Press
[10] 웹사이트 3D Fermi Surface Site http://www.phys.ufl.[...] Phys.ufl.edu 1998-05-27
[11] 서적 Electronics (fundamentals And Applications) https://books.google[...] New Age International
[11] 서적 Semiconductor Physics and Applications https://books.google[...] OUP Oxford 2000-09-01
[12] 일반텍스트
[13] 학술지 The chemical potential of an ideal intrinsic semiconductor 2004-05-01
[14] 학술지 Theory of Coulomb-blockade oscillations in the conductance of a quantum dot https://openaccess.l[...]


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com