페리 수열

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 성질
4. 예시
5. 응용
6. 리만 가설과의 관계
참조

1. 개요

페리 수열은 1802년 샤를 아로에 의해 처음 도입되었으며, 존 페리에 의해 재발견되어 널리 알려진 수열이다. 이 수열은 0과 1 사이의 모든 기약 분수를 분모의 크기 순으로 나열한 것으로, 수열의 길이는 오일러 피 함수를 사용하여 표현할 수 있다. 페리 수열의 인접한 항 사이에는 특정 관계가 성립하며, 연분수와 포드 원과도 밀접한 관련이 있다. 페리 수열은 무리수의 유리수 근삿값 계산, 물리 시스템의 공진 위치 계산, 경로 계획 연구 등 다양한 분야에 응용되며, 리만 가설과도 연관성을 갖는다.

더 읽어볼만한 페이지

수론 - 타원곡선
타원곡선은 체 위에서 정의되고 특이점이 없으며 종수가 1인 사영 대수 곡선으로, 유리점을 가지며, 특정 형태의 방정식으로 표현되고, 실수체 위에서는 연결 성분 개수가 판별식에 따라 달라지며, 복소수체 위에서는 원환면과 위상적으로 동형이고, 점들 간에 군 연산이 정의되어 암호학 및 정수론에 활용된다.
수론 - 최소공배수
최소공배수는 둘 이상의 정수들의 공배수 중 가장 작은 양의 정수로서, 소인수분해나 최대공약수와의 관계를 이용하여 구할 수 있으며, 분수 통분이나 기어 회전 수 계산 등 여러 분야에 응용된다.

페리 수열
개요
정의	n 이하의 분모를 갖는 기약분수를 크기 순으로 나열한 수열
표기	F
범위	과 사이의 유리수
예시	F = , , , , , , , , , ,
성질
이웃하는 두 항	a/b와 c/d가 이웃하는 항이면 bc-ad=1이다.
메디안트	이웃하는 두 항 a/b와 c/d의 메디안트 (a+c)/(b+d)는 두 항 사이에 존재한다.
활용
디리클레 근사 정리	모든 무리수 α에 대해 무한히 많은 유리수 p/q가 \|α - p/q\| < 1/q²를 만족한다.
포드 원	페리 수열의 각 분수에 대응하는 원을 그려 시각화한다.

2. 역사

페리 수열은 1802년 프랑스의 수학자 샤를 아로/Charles Haros^영어가 처음으로 도입하였다.^[4] 1816년 영국의 지질학자 존 페리 1세(John Farey, Sr.)가 페리 수열을 재발견하고, 이 수열의 성질에 대한 추측을 발표하면서 널리 알려지게 되었다.^[3]^[4] 페리의 추측은 오귀스탱 루이 코시에 의해 증명되었으며, 이후 페리 수열이라는 이름으로 불리게 되었다.^[4] 비록 페리가 최초 발견자는 아니지만, 그의 이름을 따서 명명된 것은 스티글러의 명명법칙의 한 예시로 볼 수 있다.^[4]

3. 성질

3. 1. 수열의 길이

n번째 페리 수열 $F_n$의 길이는 오일러 피 함수(φ)를 이용하여 표현할 수 있다.^[5] $F_n$의 길이와 $F_{n+1}$의 길이 차이는 n+1보다 작으면서 n+1과 서로소인 자연수의 개수와 같다. 페리 수열의 길이에 관한 점화식은 다음과 같다.^[5]

$|F_{n+1}| = |F_n| + \varphi(n+1)$

$|F_n|$은 계차가 $\varphi(n)$인 계차수열이고 $|F_1|=2$이기 때문에, 시그마 기호를 사용하여 $F_n$의 일반항을 나타낼 수 있다.

$|F_n| = 1 + \sum_{m=1}^n \varphi(m)$

$F_n$의 점근적 행동은 다음과 같다.

$|F_n| \sim \frac {3n^2}{\pi^2}$

3. 2. 인접한 항

페리 수열

F_n

의 연속된 두 항을

h_1/k_1

,

h_2/k_2

라고 하면,

k_1h_2 - k_2h_1 = 1

이 성립한다.^[29] 따라서 연속된 두 항의 차는

\frac{h_2}{k_2}-\frac{h_1}{k_1}=\frac{1}{k_1k_2}

와 같이 각 항의 분모를 곱한 값의 역수로 표현된다.^[29]

연속된 세 항

h_1/k_1

,

h_2/k_2

,

h_3/k_3

에 대해서는,

\frac{h_2}{k_2}=\frac{h_1+h_3}{k_1+k_3}

가 성립한다. 이 두 성질은 서로를 함축한다.^[29]

한편, 인접한 두 항의 중항

\frac{h_1+h_2}{k_1+k_2}

의 분모

k_1+k_2

는 항상

n

보다 크다. 이 중앙값은

k_1+k_2

번째 페리 수열

F_{k_1+k_2}

에 처음 등장하며, 항상

\left( \frac{h_1}{k_1} , \frac{h_2}{k_2} \right)

구간 사이에 존재한다.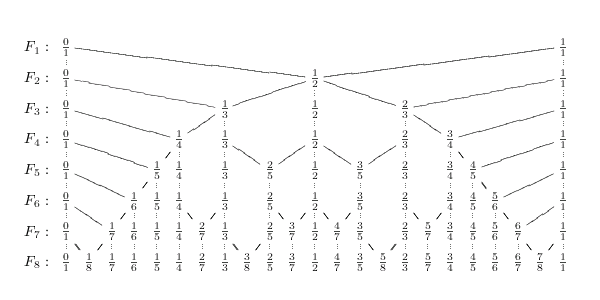

, 부터 중간수를 반복적으로 취함으로써 얻어지는 1부터 8까지에 대응하는 페리 수열

만약

\frac{a}{b}

와

\frac{c}{d}

가 어떤 페리 수열에서 인접한다면, 이 두 분수 사이에 새로운 분수가 더해지는 것은 차수

b+d

의 페리 수열에서이며, 이는

\frac{a}{b}

와

\frac{c}{d}

의 중간수(Mediant (mathematics))인

\frac{a+c}{b+d}

이다. 예를 들어,

F_5

에서는 인접한

\frac{1}{3}

과

\frac{2}{5}

사이에 나타나는 첫 번째 항은

F_8

의

\frac{3}{8}

이다.

페리 수열의 연속된 두 유리수 쌍은 면적이 1로 같다.^[8]

슈테른-브로코 나무(Stern–Brocot tree)는 0과 1에서 시작하여 연속적인 중항을 취하여 페리 수열이 구성되는 방식을 보여주는 데이터 구조이다.

3. 3. 연분수

페리 수열에서 인접한 분수는 연분수 전개와 밀접한 관련이 있다. 모든 분수는 마지막 항이 1인 두 가지 연분수 전개를 가진다. 페리 수열에 처음 나타나는 분수의 연분수 전개를 통해, 이웃하는 분수의 연분수 전개를 구할 수 있다.

예를 들어, 3/8은 [0; 2, 1, 1, 1]과 [0; 2, 1, 2] 두 가지 연분수 전개를 가지며, F₈에서의 이웃은 2/5로 [0; 2, 1, 1]로 전개될 수 있고, 1/3은 [0; 2, 1]로 전개될 수 있다.

3. 4. 포드 원

페리 수열은 포드 원과 관련이 있다.^[19]

모든 기약 분수 p/q에 대해, 반지름이 1/(2q²)이고 중심이 (p/q, 1/(2q²))인 포드 원 C[p/q]가 존재한다.^[19] 서로 다른 분수에 대한 두 포드 원은 서로소이거나 접하며, 교차하지 않는다.^[19] 0 < p/q < 1인 경우, C[p/q]에 접하는 포드 원은 페리 수열에서 p/q의 이웃인 분수에 대한 포드 원이다.^[19]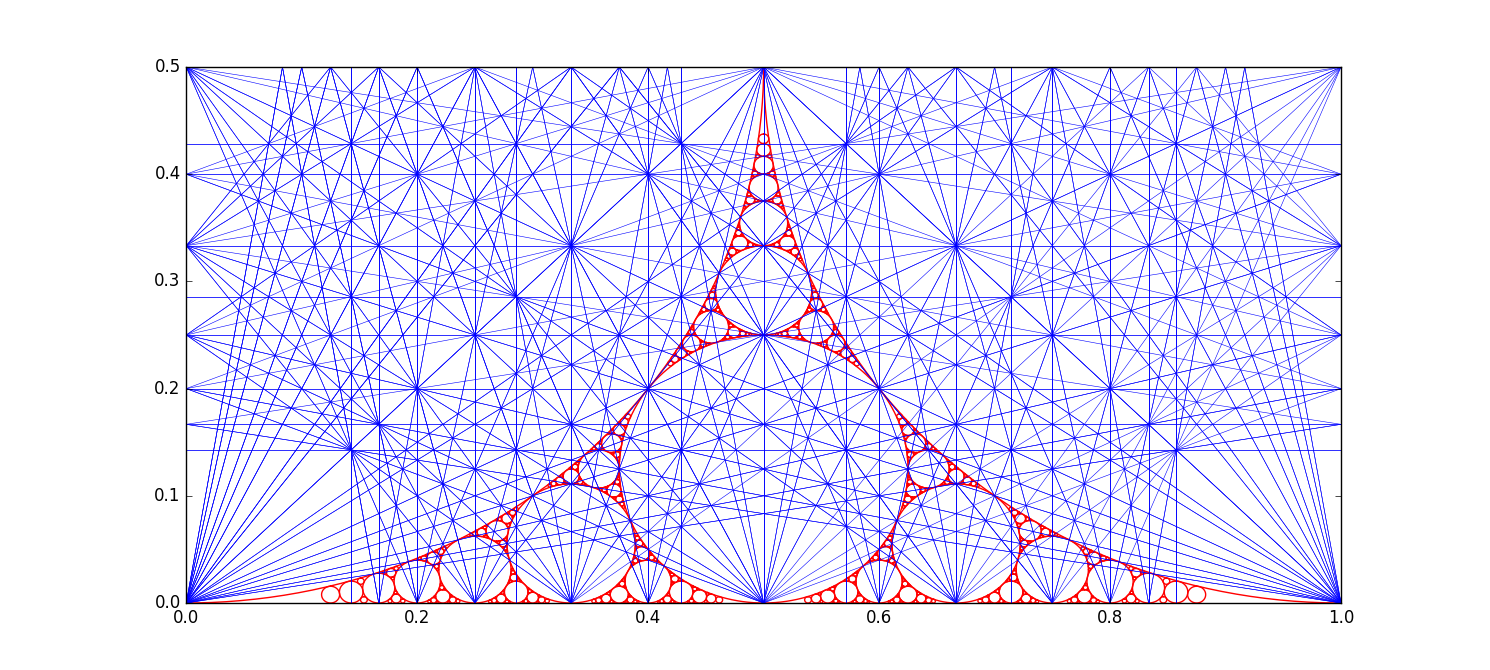

Ford 원과 원호가 있는 페리 다이어그램(Farey diagram)을 1부터 9까지의 ''n''에 대해 비교한 그림. 각 원호는 해당하는 원과 직각으로 교차한다. SVG 이미지에서 원이나 곡선 위에 마우스를 올리면 강조 표시되고 해당 용어가 강조 표시된다.

아폴로니안 개스킷(Apollonian gasket) 및 페리 공명 다이어그램.

4. 예시

''n''=1…8까지의 페리 수열은 다음과 같다.^[28]

:''F''₁ = {0/1, 1/1}

:''F''₂ = {0/1, 1/2, 1/1}

:''F''₃ = {0/1, 1/3, 1/2, 2/3, 1/1}

:''F''₄ = {0/1, 1/4, 1/3, 1/2, 2/3, 3/4, 1/1}

:''F''₅ = {0/1, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 1/1}

:''F''₆ = {0/1, 1/6, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 5/6, 1/1}

:''F''₇ = {0/1, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 2/5, 3/7, 1/2, 4/7, 3/5, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 1/1}

:''F''₈ = {0/1, 1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8, 1/1}

5. 응용

페리 수열은 무리수의 유리수 근삿값을 찾는 데 매우 유용하다.^[13] 예를 들어, Eliahou^[14]는 3''x''+1 과정에서 비자명 사이클의 길이에 대한 하한을 구성할 때 페리 수열을 사용했다.

공진 현상이 있는 물리적 시스템에서 페리 수열은 1차원^[15] 및 2차원^[16]에서 공진 위치를 계산하는 효율적인 방법을 제공한다.

페리 수열은 사각형 격자에서 임의 각도 경로 계획 연구에서 계산 복잡성^[17] 또는 최적성을 특성화하는 데 사용된다.^[18]

비선형 역학에서 두 진동자가 비선형적인 영향을 서로 주고받을 때, 이들의 진동수가 특정한 유리수 비를 갖는 인입 현상이 발생할 수 있다. 이 때 유리수 비가 나타나는 순서는 슈테른-브로코 나무의 구성과 관련이 있다.

6. 리만 가설과의 관계

페리 수열은 리만 가설의 두 가지 동치 표현에 사용된다.^[20]^[21] }}의 항을 $\{a_{k,n} : k = 0, 1, \ldots, m_n\}.$ 이라고 하자. $d_{k,n} = a_{k,n} - \tfrac{k}{m_n}$ 으로 정의한다. 다시 말해 $d_{k,n}$ 은 번째 페리 수열의 번째 항과 단위 구간에 균등하게 분포된 동일한 수의 점 집합의 번째 멤버 간의 차이이다. 1924년 제롬 프랑넬은 다음 명제가 리만 가설과 동치임을 증명했고,^[20] 이후 에드문트 란다우는 (프랑넬의 논문 직후) 다음 명제 또한 리만 가설과 동치임을 언급했다.^[21]

: $\sum_{k=1}^{m_n} d_{k,n}^2 = O (n^r) \quad \forall r > -1$

: $\sum_{k=1}^{m_n} |d_{k,n}| = O (n^r) \quad \forall r > \frac{1}{2}$

참조

_[1] 서적 An Introduction to the Theory of Numbers John Wiley and Sons
_[2] 서적 A Motif of Mathematics: History and Application of the Mediant and the Farey Sequence Docent Press 2020-09-28
_[3] 서적 An Introduction to the Theory of Numbers https://archive.org/[...] Oxford University Press
_[4] 서적 Recreations in the Theory of Numbers Dover
_[5] OEIS
_[6] 학술지 Farey Fractions with Equal Numerators and the Rank of Unit Fractions https://math.colgate[...] 2024-07
_[7] 학술지 Partial Franel sums https://cs.uwaterloo[...] 2022-01
_[8] 웹사이트 Trees, Teeth, and Time: The mathematics of clock making http://www.ams.org/p[...] 2020-09-28
_[9] arXiv A product of Gamma function values at fractions with the same denominator
_[10] arXiv The LCM(1,2,...,n) as a product of sine values sampled over the points in Farey sequences
_[11] 학술지 Equalities between greatest common divisors involving three coprime pairs http://rtomas.web.ce[...] 2020-08
_[12] 학술지 Partial Franel sums https://cs.uwaterloo[...] 2022-01
_[13] 웹사이트 Farey Approximation https://nrich.maths.[...] 2018-11-18
_[14] 학술지 The 3x+1 problem: new lower bounds on nontrivial cycle lengths 1993-08
_[15] 학술지 Quantum Revivals of Morse Oscillators and Farey–Ford Geometry
_[16] 학술지 From Farey sequences to resonance diagrams http://cds.cern.ch/r[...]
_[17] 학술지 Optimal Any-Angle Pathfinding In Practice 2016-05-26
_[18] 학술지 The Length of Shortest Vertex Paths in Binary Occupancy Grids Compared to Shortest ''r''-Constrained Ones 2017-08-19
_[19] arXiv Imperfections and corrections
_[20] 학술지 Les suites de Farey et le problème des nombres premiers http://www.digizeits[...]
_[21] 학술지 Bemerkungen zu der vorstehenden Abhandlung von Herrn Franel http://www.digizeits[...]
_[22] 학술지 Some Characteristic Properties of the Farey Series
_[23] 학술지 Farey Sums and Dedekind Sums
_[24] 학술지 The Index of a Farey Sequence
_[25] 서적 Riemann's Zeta Function Academic Press 2020-09-30
_[26] 간행물 Computing Farey series 2008-03
_[27] 문서 狭間節子, 橋本是浩「数学的活動の形成についての研究-ジオボードを活用した実践的教材開発」 https://kaken.nii.ac[...]
_[28] OEIS
_[29] 서적

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com