평균 무고장 시간

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의 및 수학적 설명
- 2.1. 수학적 표현
3. 응용 분야
- 3.1. 제조 분야에서의 활용
- 3.2. 컴퓨터 시스템에서의 활용
4. 구성 요소 네트워크에서의 MTBF 및 MDT
- 4.1. 직렬 연결
- 4.2. 병렬 연결
5. MTBF의 변형
- 5.1. MTTFd
6. 중도 절단을 고려한 MTBF
7. 한계점 및 주의사항
참조

1. 개요

평균 무고장 시간(MTBF)은 시스템의 신뢰성을 나타내는 지표로, 고장 없이 작동할 것으로 예상되는 평균 시간을 의미한다. MTBF는 고장 시점을 나타내는 임의 변수의 기대값으로 정의되며, 시스템 가동 시간/고장 횟수로 계산할 수 있다. MTBF는 시스템의 고장률이 일정하다는 가정하에 고장률의 역수로 표현되며, 시스템의 신뢰성 평가 및 서로 다른 시스템 간의 비교에 활용된다. MTBF는 직렬 및 병렬 연결된 구성 요소 네트워크의 MTBF를 계산하는 데 사용되며, 평균 다운 시간(MDT)과 함께 시스템의 가용성을 평가하는 데 기여한다. MTBF는 시스템의 "평균 수명"을 나타내므로, MTBF를 기반으로 한 확률적 고장 예측은 체계적인 고장이 없음을 의미하며, MTTFd와 같은 변형된 개념도 존재한다. MTBF는 중도 절단된 관측치를 고려하여 더욱 정확하게 계산될 수 있지만, 시스템의 마모나 경년 열화를 고려하지 못하는 한계가 있다.

더 읽어볼만한 페이지

분석 - 마음
마음은 의식, 사고, 지각, 감정, 동기, 행동, 기억, 학습 등을 포괄하는 심리적 현상과 능력의 총체이며, 다양한 분야에서 연구되고 인간 삶의 중추적인 역할을 한다.
분석 - 인용 분석
오류 - 민간어원
민간어원은 단어의 어원에 대한 잘못된 대중적 통념으로 인해 단어의 형태, 발음, 의미가 변화하는 현상으로, 언중의 해석이 언어 변화의 원인이 되며, 한국어에서는 한자어와 관련된 사례가 많고, 언어 변화, 사회문화적 맥락 등 다양한 분야와 관련되어 연구된다.
오류 - 시행착오
시행착오는 문제 해결을 위해 다양한 시도를 반복하며 실패를 통해 학습하는 과정으로, 계층적인 구조로 확장되어 문제 해결 능력을 향상시키고, 신약 개발, 유전 알고리즘, 생물학적 진화 등 다양한 분야에서 활용되는 해결책 중심적인 학습 전략이다.

평균 무고장 시간
정의
평균 고장 간격 (MTBF)	작동 중 시스템의 고유한 고장 간 예상 시간
설명
개요	MTBF는 시스템의 신뢰성을 나타내는 척도로 사용된다.
계산	MTBF는 수리 가능한 시스템에 대해서만 정의된다.
단위	시간 (일반적으로 시간, 일, 년 단위)
활용
신뢰성 공학	시스템의 신뢰성을 분석하고 개선하는 데 사용
유지보수	유지보수 일정을 계획하고 최적화하는 데 사용
의사 결정	제품의 수명 주기 비용을 평가하고 제품 선택에 대한 의사 결정을 내리는 데 사용
관련 지표
평균 수리 시간 (MTTR)	고장난 시스템을 수리하는 데 걸리는 평균 시간
평균 고장 시간 (MTTF)	수리 불가능한 시스템의 고장까지의 예상 시간
가용성	시스템이 작동 가능한 상태로 유지되는 시간의 비율
주의사항
MTBF의 한계	MTBF는 시스템의 전체 수명을 나타내는 것이 아니며, 특정 작동 조건에서만 유효하다.
MTBF의 오해	MTBF는 시스템이 해당 시간 동안 반드시 작동한다는 것을 의미하지 않는다.

2. 정의 및 수학적 설명

평균 무고장 시간(MTBF, Mean Time Between Failures)은 수리 가능한 시스템에서 고장이 발생하고 다음 고장이 발생하기까지의 평균 시간을 의미한다. 예를 들어, 동일한 시스템 3개를 가동했을 때 각각 100시간, 120시간, 130시간 후에 고장이 발생했다면, MTBF는 이 세 시간의 평균인 116.667시간이 된다.

위 그림에서 볼 수 있듯이, MTBF는 작동 시간의 총합을 고장 횟수로 나눈 값으로 계산할 수 있다.

:

\text{MTBF} = \frac{\sum{(\text{다운 시간 시작} - \text{가동 시간 시작})}}{\text{고장 횟수}}.

이와 유사하게, 평균 다운 시간(MDT, Mean Down Time)은 다음과 같이 정의된다.

:

\text{MDT} = \frac{\sum{(\text{가동 시간 시작} - \text{다운 시간 시작})}}{\text{고장 횟수}}.

일반적으로 MTBF는 시스템이 "유효 수명 기간" 내에서 작동한다고 가정한다. 이 기간 동안에는 고장률이 비교적 일정하게 유지되며, 이는 욕조 곡선에서 무작위 고장만 발생하는 중간 부분에 해당한다.^[1]

MTBF는 고장 간 평균 간격을 나타내며, 이 값이 클수록 시스템의 신뢰성이 높다고 할 수 있다. 고장률은 MTBF의 역수로, '고장률 = 1 / MTBF'로 계산된다.

MTBF는 내용 연수를 나타내는 지표로는 유용하지 않다. MTBF는 고장률 곡선에서 고장률이 일정한 시간 영역을 전제로 계산되는데, 마모형 고장(고장률이 시간이 지남에 따라 증가하는 영역)은 일반적으로 고려되지 않기 때문이다. 따라서 내용 연수를 산출하려면 가속 열화 시험 등을 활용해야 한다.

그럼에도 불구하고 MTBF는 시스템이나 부품의 신뢰성을 하나의 값으로 간결하게 표현할 수 있다는 장점이 있다. 예를 들어, 1개의 시스템을 100만 시간 동안 가동하여 10번 고장났다면 MTBF는 10만 시간이 된다. 실제로는 동일한 시스템을 여러 개 준비하여 총 가동 시간을 늘리고, 이를 통해 MTBF를 산출한다.

2. 1. 수학적 표현

MTBF는 고장 시점을 나타내는 임의 변수

T

의 기대값이다. 따라서 다음과 같이 쓸 수 있다.^[4]

:

\text{MTBF} = \mathbb{E}\{T\} = \int_0^\infty tf_T(t)\, dt

여기서

f_T(t)

는

T

의 확률 밀도 함수이다. MTBF는 신뢰도 함수

R_T(t)

를 사용하여 표현할 수도 있다.

:

\text{MTBF} = \int_0^\infty R(t)\, dt

.

MTBF와

T

는 시간 단위(예: 시간)를 갖는다.

고장률이 일정하다(

\lambda

)고 가정하면, MTBF는 고장률의 역수로 주어진다.^[1]^[4]

:

\text{MTBF} = \frac{1}{\lambda}

.

시스템의 MTBF가 알려지고, 일정한 고장률을 가정하면, 특정 시스템이 주어진 기간 동안 작동할 확률은 지수 분포의 신뢰도 함수

R_T(t) = e^{-\lambda t}

에서 추론할 수 있다.^[1] 특히, 특정 시스템이 MTBF까지 생존할 확률은

1/e

, 즉 약 37%이다(즉, 확률 63%로 더 빨리 고장난다).^[5]

3. 응용 분야

MTBF는 시스템 신뢰성의 매개변수 또는 서로 다른 시스템이나 설계를 비교하는 데 사용될 수 있다. 이 값은 "평균 수명"으로 조건부로 이해해야 하며, 작동하는 장치와 고장난 장치 간의 정량적 동일성으로 이해해서는 안 된다.^[1] 많은 엔지니어는 시간 ''t'' = MTBF에 의해 항목의 50%가 고장날 것이라고 잘못 가정하기도 한다.^[4]

MTBF 값 예측은 제품 개발의 중요한 요소이며, 신뢰성 엔지니어와 설계 엔지니어는 신뢰성 소프트웨어를 사용하여 다양한 방법과 표준(MIL-HDBK-217F, Telcordia SR332, Siemens SN 29500, FIDES, UTE 80-810 (RDF2000) 등)에 따라 제품의 MTBF를 계산한다.

MTBF는 전사적 설비 보전(TPM)에서 핵심 성과 지표(KPI)로 활용되어, 유지보수 일정 및 예비 부품 재고 관리에 대한 의사 결정을 지원한다.^[7]

MTBF에는 연속 동작 시(CCS)와 간헐 동작 시(ICAS)의 2가지 종류가 있다. 일반적으로 CCS 쪽이 조건이 더 엄격하여 MTBF가 짧지만, 형광등, HDD, 브라운관 텔레비전, 자동차(발진 가속 시), 비행기(이륙 시, 가압 시) 등에서는 기동 시에 큰 부하가 걸리기 때문에 CCS보다 ICAS 쪽이 MTBF가 짧아지는 경우가 있다. 원자로 (정지 시), 고로 (정지 시), 비행기 (착륙 시), 컴퓨터 (셧다운) 등에서는 정지 시에도 큰 부하가 걸리기 때문에, ICAS에서의 MTBF가 짧아지는 경향이 있다.

3. 1. 제조 분야에서의 활용

평균 무고장 시간(MTBF)은 기계 및 장비 신뢰성을 관리하는 데 중요한 지표이다. MTBF는 전사적 설비 보전(TPM)의 맥락에서 특히 중요한데, 장비 효율성을 극대화하는 것을 목표로 하기 때문이다. MTBF는 정상 작동 중 시스템 고장 사이의 경과 시간을 정량적으로 측정하여, 제조 장비의 신뢰성과 성능에 대한 통찰력을 제공한다.^[6]

제조업체는 MTBF를 TPM 원칙과 통합함으로써, 더욱 사전 예방적인 유지보수 방식을 달성할 수 있다. 이러한 통합을 통해 고장이 발생하기 전에 패턴과 잠재적인 고장을 식별하여 예방 유지보수를 수행하고 계획되지 않은 가동 중단을 줄일 수 있다. 결과적으로 MTBF는 TPM 내에서 핵심 성과 지표(KPI)가 되어 유지보수 일정, 예비 부품 재고에 대한 의사 결정을 안내하고 궁극적으로 기계의 수명과 효율성을 최적화한다.^[7] MTBF를 전략적으로 사용하면 전반적인 생산 효율성이 향상되고, 고장과 관련된 비용이 절감되며, 제조 프로세스의 지속적인 개선에 기여한다.

3. 2. 컴퓨터 시스템에서의 활용

RASIS는 컴퓨터 시스템의 신뢰성을 종합적으로 평가하는 기준이다. RASIS는 다음의 머리글자로 구성된다.

'''R'''eliability (신뢰성)
'''A'''vailability (가용성)
'''S'''erviceability (보수성)
'''I'''ntegrity (보전성)
'''S'''ecurity (기밀성)

신뢰성(Reliability)은 시스템이 안정적으로 계속 작동하는 시간으로, 평균 무고장 시간(MTBF)이 하나의 지표이다. 이와 대조적인 지표로 보수성(Serviceability)^[14]이 있다. 평균 수리 시간(Mean Time To Repair, MTTR)은 시스템의 보수성을 나타내는 지표이며, 수리에 소요되는 평균 시간으로 산출된다.

평균 무고장 시간(MTBF, 신뢰성의 지표)와 평균 수리 시간(MTTR, 보수성의 지표)로부터 시스템의 가용성(Availability) 지표인 가동률이 도출된다. 평균 무고장 시간이 크고 평균 수리 시간이 작은 시스템일수록 가용성이 높으며, 종합적인 신뢰성이 높은 시스템이라고 할 수 있다.

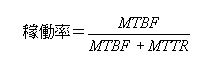
4. 구성 요소 네트워크에서의 MTBF 및 MDT

둘 이상의 구성 요소가 직렬 또는 병렬로 연결된 네트워크에서, 전체 시스템의 평균 무고장 시간(MTBF) 및 평균 다운 타임(MDT)은 개별 구성 요소의 MTBF 및 MDT를 사용하여 계산할 수 있다.^[8]^[9]

두 구성 요소가 직렬로 연결된 경우, 둘 중 하나라도 고장나면 네트워크 전체가 고장난다. 반면, 병렬로 연결된 경우에는 두 구성 요소 모두 고장 나야 네트워크가 고장난다.

직렬 및 병렬 연결에서의 MDT 계산 공식은 다음과 같다.

직렬 연결 시스템의 MDT:^[8]

:

\text{mdt}(c_1 ; c_2) = \frac{\text{mtbf}(c_1)\times \text{mdt}(c_2) + \text{mtbf}(c_2)\times \text{mdt}(c_1)}  {\text{mtbf}(c_1) + \text{mtbf}(c_2)}\;,

병렬 연결 시스템의 MDT:^[8]

:

\text{mdt}(c_1 \parallel c_2) = \frac{\text{mdt}(c_1)\times \text{mdt}(c_2)}  {\text{mdt}(c_1) + \text{mdt}(c_2)}\;.

여러 개의 직렬 구성 요소가 있을 때, MDT는 다음과 같이 일반화할 수 있다.^[10]

:

\text{mdt}(c_1\parallel\dots\parallel c_n) = \left(\sum_{k=1}^n \frac 1{\text{mdt}(c_k)}\right)^{-1}\;,

4. 1. 직렬 연결

두 개의 구성 요소

c_1, c_2

(예: 하드 드라이브, 서버 등)는 직렬로 네트워크를 구성할 수 있다. 여기서 사용된 용어는 전기 회로와 매우 유사하지만 약간 다른 의미를 갖는다. 두 구성 요소 중 하나라도 고장이 나면 네트워크 전체에 고장이 발생한다.^[8]^[9]

수리 가능한 구성 요소가 있는 직렬 시스템의 평균 무고장 시간(MTBF)은 개별 구성 요소의 MTBF가 모두 알려져 있다고 가정할 때 다음 공식으로 계산할 수 있다.^[8]^[9]

:

\text{mtbf}(c_1 ; c_2) = \frac{1}{\frac{1}{\text{mtbf}(c_1)} + \frac{1}{\text{mtbf}(c_2)}} = \frac{\text{mtbf}(c_1)\times \text{mtbf}(c_2)}  {\text{mtbf}(c_1) + \text{mtbf}(c_2)}\;,

여기서

c_1 ; c_2

는 구성 요소가 직렬로 배열된 네트워크이다.

이 공식은 고장 확률의 관점에서 설명할 수 있다. 특정 기간 내에 시스템이 고장날 확률은 MTBF의 역수이다. 일련의 구성 요소를 고려할 때, 구성 요소의 고장은 전체 시스템의 고장으로 이어지므로(고장 확률이 작다고 가정하면, 이는 일반적으로 성립한다) 주어진 간격 내에 전체 시스템의 고장 확률은 구성 요소의 고장 확률의 합으로 근사할 수 있다.

여러 직렬 구성 요소의 경우, MTBF 계산은 다음과 같이 일반화할 수 있다.

:

\text{mtbf}(c_1;\dots; c_n) = \left(\sum_{k=1}^n \frac 1{\text{mtbf}(c_k)}\right)^{-1}\;,

4. 2. 병렬 연결

두 개의 구성 요소

c_1, c_2

(예: 하드 드라이브, 서버 등)가 병렬로 연결되었다는 것은, '두 개 모두' 고장 나야 네트워크가 고장나는 경우를 의미한다.^[8]^[9]

병렬 수리 가능 구성 요소가 포함된 네트워크의 경우, 전체 시스템의 평균 무고장 시간(MTBF)을 확인하려면 구성 요소 MTBF 외에도 해당 평균 다운 타임(MDT)도 알아야 한다. MDT가 MTBF에 비해 무시할 수 있다고 가정하면 (이는 일반적으로 실제로 성립한다), 두 개의 병렬 수리 가능 구성 요소로 구성된 병렬 시스템의 MTBF는 다음과 같이 계산할 수 있다.^[8]^[9]

:

\begin{align}\text{mtbf}(c_1 \parallel c_2) &= \frac{1}{\frac{1}{\text{mtbf}(c_1)}\times\frac{\text{mdt}(c_1)}{\text{mtbf}(c_2)}+\frac{1}{\text{mtbf}(c_2)}\times\frac{\text{mdt}(c_2)}{\text{mtbf}(c_1)}}\\[1em]&= \frac{\text{mtbf}(c_1)\times \text{mtbf}(c_2)}  {\text{mdt}(c_1) + \text{mdt}(c_2)}\;,\end{align}

여기서

c_1 \parallel c_2

는 구성 요소가 병렬로 배열된 네트워크이고,

PF(c,t)

는 "취약성 기간"

t

동안 구성 요소

c

의 고장 확률이다.

직관적으로, 이 공식은 고장 확률의 관점에서 설명할 수 있다. 특정 기간 내에 시스템이 고장날 확률은 MTBF의 역수이다. 병렬 구성 요소의 경우, 전체 시스템은 한 구성 요소가 고장난 후 첫 번째 구성 요소가 수리되는 동안 다른 구성 요소가 고장날 경우에만 고장난다. 즉, 첫 번째 구성 요소가 더 빨리 수리될수록 다른 구성 요소가 고장날 수 있는 "취약성 기간"이 줄어든다.

두 개의 병렬 구성 요소로 구성된 시스템의 MDT는 다음과 같이 계산할 수 있다.^[8]

:

\text{mdt}(c_1 \parallel c_2) = \frac{\text{mdt}(c_1)\times \text{mdt}(c_2)}  {\text{mdt}(c_1) + \text{mdt}(c_2)}\;.

5. MTBF의 변형

평균 무고장 시간(MTBF)은 "시스템 중단 간 평균 시간"(MTBSA), "주요 고장 간 평균 시간"(MTBCF), "예정 외 제거 간 평균 시간"(MTBUR) 등 다양한 형태로 사용된다. 이러한 용어는 중요 고장과 중요하지 않은 고장처럼 고장 유형을 구분할 때 사용된다. 예를 들어, 자동차에서 FM 라디오 고장은 차량의 주요 작동을 막지 않는다.

MTBF는 수리 가능한 시스템의 고장 간 시간을 의미하므로, 고장 후 시스템을 교체하는(수리 불가능한 시스템) 경우에는 MTBF 대신 평균 고장 시간(MTTF)을 사용하는 것이 좋다.^[1]

5. 1. MTTFd

MTTFd는 MTTF의 확장으로, 위험한 상태를 초래하는 고장만을 고려한다. MTTFd는 다음과 같이 계산할 수 있다.^[11]

MTTF^영어 ≈ ''B''₁₀ / 0.1''n''_op

MTTFd^영어 ≈ ''B''_10d / 0.1''n''_op

여기서 ''B''₁₀은 장치가 작동할 수 있는 횟수로, 그 횟수까지 작동하면 해당 장치 샘플의 10%가 고장난다. ''n''_op는 작동 횟수이다. ''B''_10d는 동일한 계산이지만, 샘플의 10%가 위험으로 고장나는 경우이다. ''n''_op는 1년 동안의 작동/주기 횟수이다.^[11]

6. 중도 절단을 고려한 MTBF

실제로 고장만 계산하는 평균 무고장 시간(MTBF)은 아직 고장나지 않은 시스템의 부분적인 수명을 계산에 포함하지 않아 MTBF를 과소평가하게 된다. 이러한 수명은 고장 시간이 시스템이 작동한 시간을 초과한다는 것을 의미하며, 이를 중도 절단이라고 한다.^[12]

특정 날의 경험에 대한 우도는 다음과 같이 나타낼 수 있다.

: $L = \prod_i \lambda(u_i)^{\delta_i} S(u_i)$

여기서,

$u_i$ 는 고장의 경우 고장 시간, 아직 고장나지 않은 장치의 경우 중도 절단 시간이다.
$\delta_i$ 는 고장의 경우 1, 중도 절단 시간의 경우 0이다.
$S(u_i)$ 는 생존 함수로, 수명이 $u_i$ 를 초과할 확률을 의미한다.
$\lambda(u_i) = f(u)/S(u)$ 는 위험 함수로, 순간적인 사망률을 나타낸다. ( $f(u)$ 는 분포의 확률 밀도 함수)

지수 분포에서 위험(

\lambda

)이 일정할 경우, MTBF는 다음과 같이 계산된다.

:MTBF =

1 / \hat\lambda = \sum u_i / k

여기서

\hat\lambda

는 위에서 주어진 우도를 최대화하는

\lambda

의 최우 추정치이고,

k = \sum \sigma_i

는 중도 절단되지 않은 관측치의 수이다.

고장만 고려한 MTBF와 중도 절단된 관측치를 포함한 MTBF의 차이는, 중도 절단 시간이 MTBF 계산 시 분자에는 더해지지만 분모에는 더해지지 않는다는 것이다.^[12]

예를 들어, 1개의 시스템을 100만 시간 가동하여 10번 고장났다면 MTBF는 10만 시간이다. 하지만 100만 시간 동안 시스템을 계속 감시하는 것은 현실적으로 불가능하므로, 동일한 시스템 10만 개를 100시간 동안 감시하여 총 1000만 시간 가동시간 중 100개가 고장났다고 가정해도 MTBF는 동일하게 10만 시간이 된다.

이 두 예시에서 MTBF는 동일하지만, 직관적으로 전자가 더 신뢰성이 높아 보인다. 이는 후자의 시험 방법이 마모나 경년 열화를 고려하지 않기 때문이다. 장기간에 걸쳐 소수의 샘플을 사용하는 시험에서는 샘플이 마모 고장한다고 가정할 수 있지만, 단시간에 대량의 샘플을 사용하는 시험에서는 장기간 사용 가능 여부를 알 수 없다.

하지만 MTBF가 무의미한 것은 아니다. 사용자가 대량의 제품을 구매하여 내구 연한 전에 교체하는 방식으로 운용하는 경우, 초기 불량률이나 랜덤 고장기의 고장률이 중요하며, 이때 MTBF와 고장률이 중요한 지표가 된다.

7. 한계점 및 주의사항

MTBF는 "평균 수명"으로 조건부로 이해해야 하며, 작동하는 장치와 고장 난 장치 간의 정량적 동일성으로 이해해서는 안 된다.^[1] MTBF를 기반으로 한 확률적 고장 예측은 체계적인 고장이 없음을 전제로 하는데, 이는 확인하기 쉽지 않다.^[4]

MTBF는 내용 연수를 나타내는 지표로는 유용하지 않다. 왜냐하면 MTBF는 욕조 곡선에서 고장률이 일정한 구간만을 전제로 계산되며, 마모형 고장(시간이 지남에 따라 고장률이 증가하는 형태)은 고려하지 않기 때문이다. 따라서 내용 연수를 산출하려면 가속 열화 시험 등에 의존해야 한다.

그럼에도 불구하고 MTBF는 시스템이나 부품의 신뢰성을 하나의 값으로 간결하게 표현할 수 있다는 장점이 있다.

참조

_[1] 서적 Fundamentals of Electronic Systems Design Springer International Publishing 2017
_[2] 간행물 'Systems reliability assessment – Proceedings of the Ispra Course held at the Escuela Tecnica Superior de Ingenieros Navales, Madrid, Spain, September 19–23, 1988 in collaboration with Universidad Politecnica de Madrid' 1988
_[3] 웹사이트 Defining Failure: What Is MTTR, MTTF, and MTBF? http://blog.fosketts[...] 2011-07-06
_[4] 서적 Reliability Engineering: Theory and Practice Springer, Berlin 2013
_[5] 웹사이트 Reliability and MTBF Overview http://www.vicorpowe[...] Vicor Reliability Engineering 2017-06-01
_[6] 웹사이트 MTBF: What it means and how to calculate it https://total-manufa[...] 2024-02-07
_[7] 웹사이트 MTBF MTTR MTTF: TPM Indicators https://leancommunit[...] 2021-11-22
_[8] 웹사이트 Reliability Characteristics for Two Subsystems in Series or Parallel or n Subsystems in m_out_of_n Arrangement (by Don L. Lin) http://auroraconsult[...]
_[9] 서적 Reliability, Maintainability and Risk Butterworth-Heinemann
_[10] 웹사이트 MTBF Allocations Analysis1 http://www.angelfire[...] 2016-12-23
_[11] 웹사이트 B10d Assessment – Reliability Parameter for Electro-Mechanical Components https://www.tuv.com/[...] TUVRheinland 2015-07-07
_[12] Q Q98961801
_[13] 문서 JIS Z 8115:2000は、MTBFは「平均故障間動作時間」で、「故障間動作時間の期待値」と定義し、「ある特定期間中のMTBFは、その期間中の総動作時間を総故障数で除した値である。」としている。「平均故障間隔」については、「MTBFという略号は現在この意味では使われない」としている。
_[14] 문서 JIS X 0014「情報処理用語―信頼性、保守性及び可用性」においては、serviceabilityに対応する訳語は「運用性」(サービス性)であり、「保守性」に対応する英語はmaintainabilityである。

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com