표피효과
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
표피 효과는 교류가 흐르는 도체에서 전류가 도체 표면에 집중되는 현상이다. 이는 교류 전류가 생성하는 자기장의 변화가 전류 흐름에 반대하는 역기전력을 유발하기 때문이다. 표피 효과로 인해 도체의 유효 저항이 증가하고, 전류 밀도는 표면에서 가장 크고 내부로 갈수록 감소한다. 표피 깊이는 전류 밀도가 표면 값의 약 37%로 감소하는 깊이를 의미하며, 주파수가 높을수록, 도체의 저항률과 투자율이 클수록 얕아진다. 이러한 현상은 전송선로, 고주파 회로 설계, 전력 시스템 등 다양한 분야에 영향을 미치며, 리츠선, 다층 연도체, 은도금 등을 통해 완화할 수 있다.
일반적으로 전선 형태의 도체는 교류를 통해 전기 에너지 또는 신호를 전달하는 데 사용될 수 있다. 이 전류를 구성하는 전하 운반자(보통 전자)는 전기 에너지원으로부터 발생하는 전기장에 의해 구동된다. 도체의 전류는 도체 내 및 주변에 자기장을 생성한다. 도체의 전류 세기가 변하면 자기장도 변한다. 자기장의 변화는 차례로 전류 세기의 변화에 반대하는 전기장을 생성한다. 이 반대 전기장을 역기전력이라고 한다.[2][3] 역기전력은 도체의 중심에서 가장 강하게/가장 집중되어 있으며, 도체의 외부 피부 근처에서만 전류가 흐르도록 한다.
도체의 교류 전류 밀도 ''J''는 표면 ''J''S에서의 값으로부터 표면으로부터의 깊이 ''d''에 따라 지수적으로 감소한다.[4]
피부 깊이가 전선의 반지름에 비해 작지 않은 경우, 전류 밀도는 베셀 함수로 설명될 수 있다. 다른 필드의 영향에서 벗어난 원형 전선 내부의 전류 밀도는 축으로부터의 거리에 대한 함수로 다음과 같이 주어진다.[7]
2. 원인
구동력에 관계없이 전류 밀도는 도체의 표면에서 가장 크고 도체 내부로 갈수록 감소하는 것으로 나타났다. 이러한 전류 밀도의 감소를 ''표피 효과''라고 하며, ''표피 깊이''는 전류 밀도가 표면 근처 값의 1/e로 떨어지는 깊이를 측정한 것이다. 전류의 98% 이상이 표면으로부터 표피 깊이의 4배 이내의 층에서 흐를 것이다. 이러한 동작은 일반적으로 전선의 단면 전체에 균등하게 분포되는 직류와는 구별된다.
교류는 또한 유도 법칙에 따라 교류 자기장에 의해 도체에서 ''유도''될 수 있다. 따라서 도체에 충돌하는 전자기파는 일반적으로 이러한 전류를 생성하며, 이는 금속에서 전자기파의 감쇠를 설명한다. ''표피 효과''라는 용어는 전기 전류 전송과 관련된 응용 분야와 가장 자주 연관되지만, 표피 깊이는 평면파가 수직 입사로 벌크 재료에 충돌할 때 벌크 재료 내부의 전기장 및 자기장, 유도 전류의 밀도의 지수적 감소를 설명하기도 한다.
교류가 흐르는 도체 내에서는, 그 전류에 의한 자기장이 변화하므로, 그 자기장의 변화를 상쇄하려는 기전력이 발생한다.( 렌츠의 법칙) 그 기전력에 의한 와전류가 중심부에서는 교류 전류의 반대 방향으로 흐르기 때문에, 중심부일수록 전류는 흐르기 어려워진다.[25]
3. 공식
:
여기서 는 '스킨 깊이'라고 불리며, 이는 전류 밀도가 ''J''S의 1/e (약 0.37)로 감소하는 도체 표면 아래의 깊이로 정의된다. 지수의 허수 부분은 전류 밀도의 위상이 스킨 깊이당 1 라디안만큼 위상 지연됨을 나타낸다. 도체 내에서 하나의 완전한 파장은 2 스킨 깊이를 필요로 하며, 이때 전류 밀도는 e−2 (1.87×, 또는 −54.6 dB)로 표면 값에서 감쇠한다. 도체 내의 파장은 진공에서의 파장보다 훨씬 짧으며, 이는 도체 내의 위상 속도가 진공에서의 광속보다 훨씬 느리다는 것과 같다. 예를 들어, 1 MHz의 전파는 진공에서의 파장 가 약 300 m인 반면, 구리에서는 파장이 약 0.5 mm로 줄어들고 위상 속도는 약 500 m/s에 불과하다. 스넬의 법칙과 도체 내의 이 매우 작은 위상 속도의 결과로, 도체에 입사하는 모든 파는, 심지어 접선 입사에서도, 본질적으로 도체의 표면에 수직인 방향으로 굴절된다.[4]
유전 손실이나 자기 손실이 없는 경우 스킨 깊이에 대한 일반적인 공식은 다음과 같다.[5]
:
여기서
보다 훨씬 낮은 주파수에서는 큰 괄호 안의 값이 1에 가깝고, 공식은 일반적으로 다음과 같이 주어진다.
:
이 공식은 강한 원자 또는 분자 공진에서 멀리 떨어진 주파수와 물질의 플라즈마 주파수 및 전도 전자를 포함하는 충돌 사이의 평균 시간의 역수보다 훨씬 낮은 주파수에서 유효하다. 금속과 같은 좋은 도체에서는 이러한 모든 조건이 적어도 마이크로파 주파수까지 보장되므로 이 공식의 유효성을 정당화한다.[6]
그러나 매우 불량한 도체에서는 충분히 높은 주파수에서 큰 괄호 안의 값이 증가한다. 보다 훨씬 높은 주파수에서 스킨 깊이는 점근선 값에 접근한다.
:
이 일반 공식과의 편차는 전도율이 상당히 낮고 진공 파장이 스킨 깊이 자체보다 그다지 크지 않은 주파수의 재료에만 적용된다. 예를 들어, 벌크 실리콘(비도핑)은 불량한 도체이며 100 kHz( = 3 km)에서 약 40 미터의 스킨 깊이를 갖는다. 그러나 주파수가 메가헤르츠 범위로 증가함에 따라 스킨 깊이는 11 미터의 점근선 값 아래로 떨어지지 않는다.
켈빈 경은 1887년에 표피 효과를 설명했다. 도체의 전류 밀도 ''J''는 깊이 ''δ''에 대해, 다음 식으로 감소한다.
:
여기서 d는 표피 깊이로, 전류가 표면 전류의 1/e (약 0.37)가 되는 깊이이며 다음과 같이 계산된다.
:
여기서
d의 두께를 가진 평판이 직류 전류에 대해 나타내는 저항과, 두께가 d보다 훨씬 두꺼운 평판의 교류 전류에 대한 저항은 같다. 교류 전류에 대해 전선은 직류 전류에 대한 두께 d의 파이프와 같은 저항을 나타낸다. 예시로, 원형 단면의 전선의 저항은 대략 다음과 같다.
:
여기서
의 경우 위의 근사는 유효하다.
4. 원형 도선
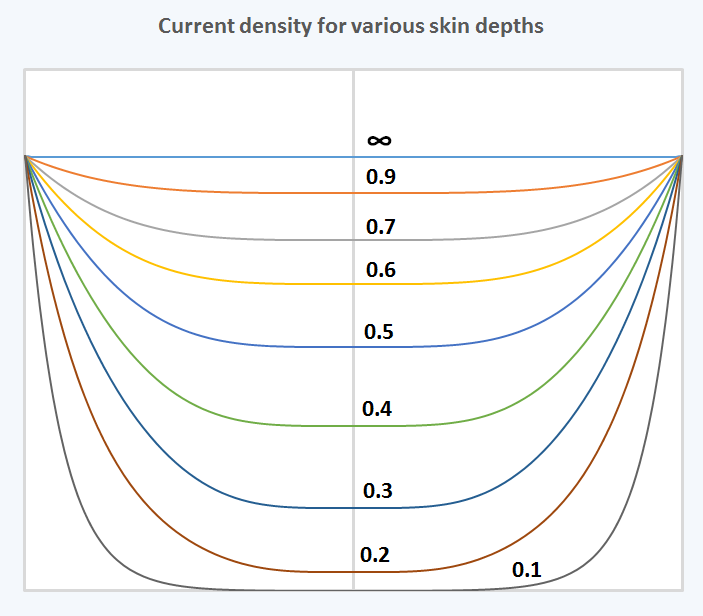
:
여기서
가 복소수이므로, 베셀 함수도 복소수이다. 전류 밀도의 진폭과 위상은 깊이에 따라 변한다.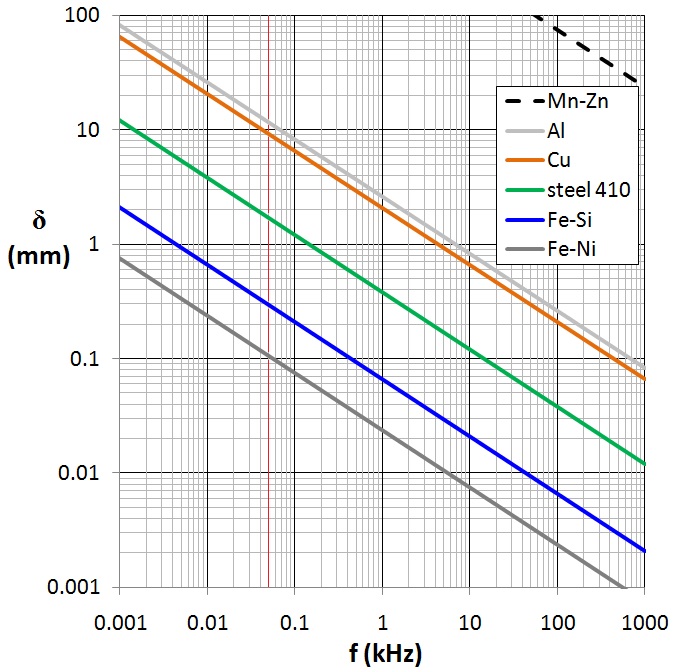
구리선의 경우, 주파수에 대한 표피 깊이 d는 아래 표와 같다.
| 주파수 | 표피 깊이 d |
|---|---|
| 60Hz | 8.57mm |
| 10kHz | 0.66mm |
| 10MHz | 21μm |
4. 1. 임피던스
4. 1. 1. 저항
표피 효과가 단일 전선의 임피던스에 미치는 가장 중요한 영향은 전선의 저항 증가와 그에 따른 손실이다. 큰 도체(δ보다 훨씬 두꺼움) 표면 근처에 국한된 전류로 인한 유효 저항은 해당 재료의 직류 저항률을 기반으로 δ 두께의 층을 통해 전류가 균일하게 흐르는 것처럼 계산할 수 있다. 유효 단면적은 도체의 둘레에 δ를 곱한 값과 대략 같다.따라서 δ에 비해 직경 D가 큰 전선과 같은 긴 원통형 도체는 벽 두께가 δ인 중공 튜브가 직류를 전달하는 것과 ''거의'' 같은 저항을 갖는다. 길이 ℓ 및 저항률 ρ의 전선의 교류 저항은 다음과 같다.
위의 마지막 근사는 를 가정한다.
주파수 f에서 저항이 10% 증가하는 원형 단면 전선의 직경 D에 대한 편리한 공식(F.E. 터먼에게 귀속)은 다음과 같다.[8]
이 교류 저항 증가 공식은 절연 전선에만 정확하다. 예를 들어, 케이블이나 코일과 같은 인접한 전선의 경우 교류 저항은 근접 효과의 영향을 받으며, 이는 교류 저항을 추가적으로 증가시킬 수 있다. 둥근 전선 세그먼트의 단위 길이당 ''내부'' 임피던스는 다음과 같다.[7]
이 임피던스는 전선의 내부 자기 인덕턴스로 인한 복소수 수량에 해당하며, 단위 길이당 직렬로 연결된 저항(실수)과 리액턴스 (허수)에 해당한다.
4. 1. 2. 인덕턴스
전선의 인덕턴스 중 일부는 전선 ''내부''의 자기장에 의한 것으로, 이를 ''내부 인덕턴스''라고 한다. 대부분의 경우 내부 인덕턴스는 전선 ''외부''의 자기장에 의한 유도 효과를 포함하는 외부 인덕턴스보다 작은 값을 가진다. 내부 인덕턴스는 표피 효과에 의해 감소하는데, 표피 깊이가 도체의 크기에 비해 크지 않은 주파수에서 감소한다.[9] 내부 인덕턴스는 낮은 주파수에서 (비자성 전선의 경우 50 nH/m) 값에 접근하며, 전선의 반지름에 관계없이 일정하다. 하지만 표피 깊이와 전선의 반지름 비율이 약 1 미만으로 떨어지면 주파수가 증가함에 따라 감소한다. 이는 아래 표에서 주파수가 증가함에 따라 전화선 인덕턴스가 감소하는 것을 설명한다.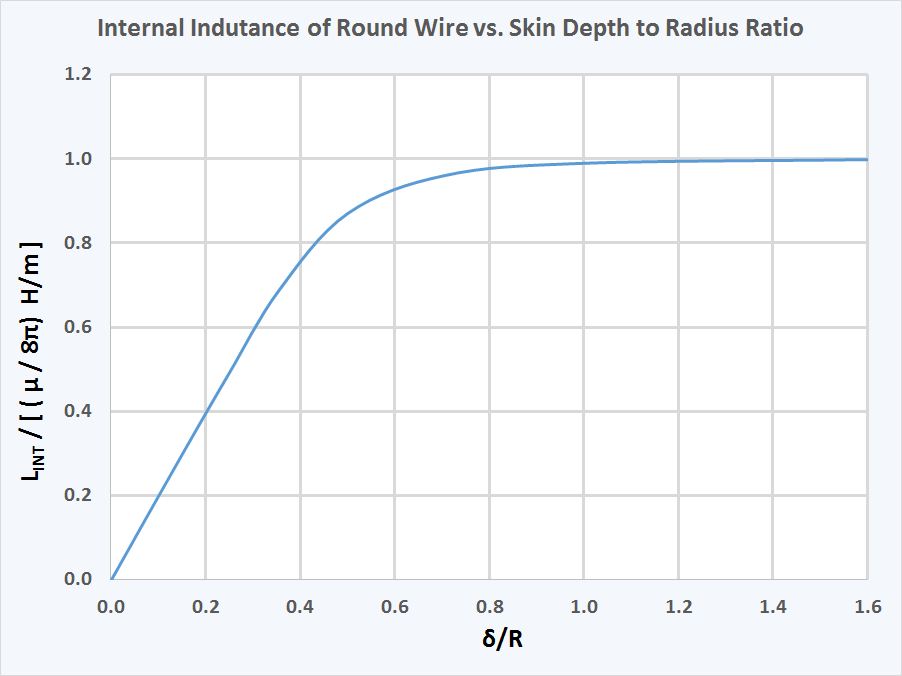
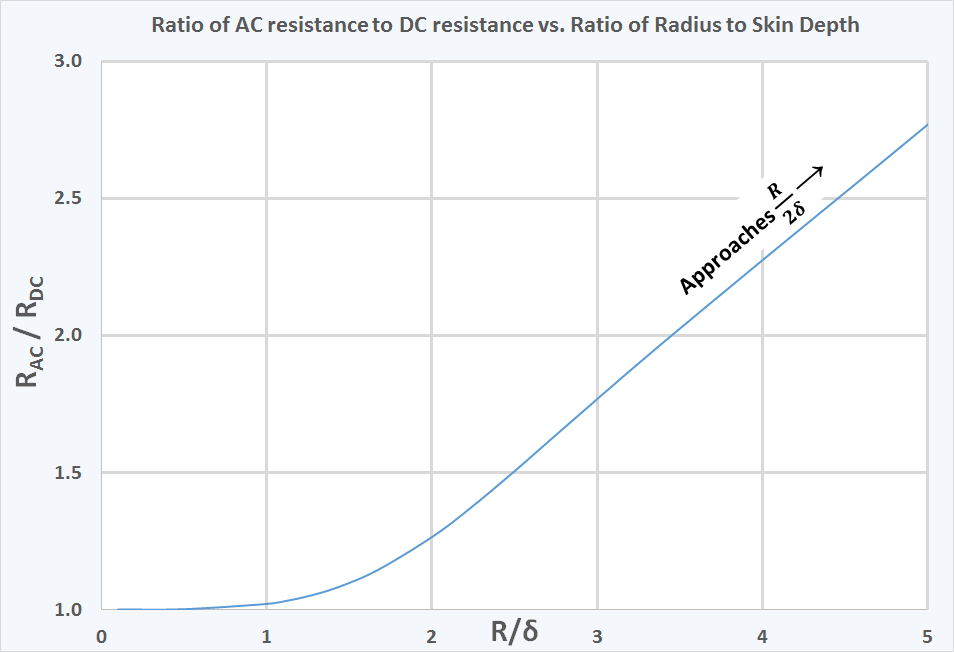
동축 케이블의 경우, 표피 효과로 인해 고주파수에서 전류가 도체 표면에 주로 흐르므로 전선 ''내부''의 자기장(대부분의 전류가 흐르는 깊이 아래의 자기장)이 감소한다. 이는 전선의 자기 인덕턴스에 미미한 영향을 준다. 이 현상에 대한 수학적 처리는 Skilling[10] 또는 Hayt[11]를 참조할 수 있다.
여기서 고려되는 인덕턴스는 회로 소자로 사용되는 코일의 인덕턴스가 아닌, 베어(bare) 도체의 인덕턴스이다. 코일의 인덕턴스는 코일 턴 사이의 상호 인덕턴스에 의해 결정되며, 턴 수의 제곱에 비례하여 증가한다. 단일 전선의 경우, 전선 외부의 자기장과 관련된 ''외부 인덕턴스'' 외에도 전선 내부의 자기장에 의한 ''내부 인덕턴스''가 존재한다. 내부 인덕턴스는 표피 깊이가 전선의 반지름보다 크지 않을 때 감소하며, 이는 고주파에서 발생한다.
단일 전선의 경우, 전선이 길어질수록 내부 인덕턴스 감소는 무시할 수 있다. 그러나 전송선의 경우, 두 번째 도체의 존재로 인해 외부 자기장 범위가 줄어들어 표피 효과로 인한 인덕턴스 감소가 중요해진다. 예를 들어, 전화 꼬임쌍선의 경우, 높은 주파수에서 도체 인덕턴스가 감소한다. 반면, 코일의 경우 외부 인덕턴스가 커서 내부 인덕턴스는 무시된다.
5. 재료의 영향
도체의 투자율과 저항률은 표피 효과에 영향을 미치는 주요 요인이다. 피부 깊이는 저항률의 제곱근에 비례하고, 투자율의 제곱근에 반비례한다.
강자성체인 철은 구리보다 투자율이 약 10,000배 높아 피부 깊이가 매우 얇다. 60 Hz에서 철의 피부 깊이는 약 220 마이크로미터로, 구리의 약 1/38 수준이다. 따라서 철선은 AC 전력선에 적합하지 않으며, 전력 변압기의 적층 손실을 증가시킨다.[15] 이러한 특성 때문에 철봉은 직류 용접에는 적합하지만, 고주파에서는 표피 효과로 인해 사용하기 어렵다. 고주파 용접에는 비자성 봉이 사용된다.[15]
도체 성능이 좋을수록 저항률이 낮아져 피부 깊이가 감소하지만, AC와 DC 저항의 비율은 더 커진다. 예를 들어, 60 Hz에서 2000 MCM (1000 제곱밀리미터) 구리 도체는 DC보다 23% 더 높은 저항을 가지며, 같은 크기의 알루미늄 도체는 DC보다 10% 더 높은 저항을 갖는다.[15]
1 메가헤르츠에서 습한 토양의 피부 효과 깊이는 약 5.0 m이고, 해수는 약 0.25 m이다.[16]
6. 경감 대책
절연 전선을 사용하거나, 다층 연도체를 사용하는 것은 표피 효과를 경감시키는 대책이다.[17] 리츠선(독일어: ''Litzendraht'', 꼬인 전선)은 수 킬로헤르츠에서 약 1 메가헤르츠 사이의 주파수에서 표피 효과를 완화하는 데 사용되는 케이블이다. 리츠선은 여러 개의 절연 전선 가닥을 엮어 만들어, 전체 자기장이 모든 전선에 동일하게 작용하여 전류가 균등하게 분배되도록 한다. 각 가닥에 표피 효과가 거의 영향을 미치지 않으므로, 단일 도체가 겪는 AC 저항 증가를 겪지 않는다.[17]
리츠선은 고주파 변압기의 권선에 사용되어 효율을 높인다. 대형 전력 변압기는 리츠선과 유사한 구조의 가닥 도체를 사용하지만, 더 큰 단면적을 사용한다.[18] 탄소 나노튜브로 구성된 전도성 실[19]은 중파에서 마이크로파 주파수에 이르는 안테나용 도체로 사용될 수 있다. 나노튜브는 표피 깊이보다 훨씬 작아서 실의 전체 단면적을 사용할 수 있으며, 매우 가벼운 안테나가 된다.
고전압, 대전류 가공 전선은 강철 보강 코어가 있는 알루미늄 케이블을 사용한다. 강철 코어의 높은 저항은 AC 전류가 거의 흐르지 않는 표피 깊이보다 훨씬 깊숙이 위치하기 때문에 문제가 되지 않는다. 수천 암페어에 이르는 높은 전류가 흐르는 경우, 고체 도체 대신 튜브를 사용하여 도체 내부를 제거한다. 이는 AC 저항에 거의 영향을 미치지 않지만, 도체의 무게를 줄인다. 튜브형 도체는 전력 개폐소에서 일반적이며, 긴 경간은 물리적인 처짐을 나타내지만, 전기적 성능에는 영향을 미치지 않는다.
고전류 상황에서 표피 효과는 금속이 굽힘 내부에서 압축되고 외부에서 늘어나는 날카로운 굽힘에서도 발생한다. 내부 표면의 짧은 경로는 낮은 저항을 유발하여 전류가 굽힘 내부 표면에 집중된다. 따라서 원형 코어가 있는 변압기는 사각형 또는 직사각형 코어를 가진 변압기보다 효율적이다.
고체 또는 튜브형 도체는 전기 도금을 통해 은으로 도금하여 전도성을 높일 수 있다. 이 기술은 VHF에서 마이크로파 주파수에서 특히 유용하다. 은 도금은 도파관 표면에도 사용되어 전파파의 감쇠를 줄인다. 표피 효과는 와전류를 도파관 구조의 얇은 표면층으로 제한하여 귀금속 사용을 실용적으로 만든다. 구리나 은과 달리 부식되지 않는 금 도금도 사용된다.
최근에는 나노미터 규모의 두께로 비자성 및 강자성 재료를 층상화하는 방법이 매우 높은 주파수에서 표피 효과로 인한 저항 증가를 완화하는 것으로 나타났다.[20] 이는 5G 통신에 영향을 미칠 수 있다.[20]
7. 전자기파
표피 효과는 침투 깊이와 관련이 있다.
전자기파에서 표피 깊이는 전기장과 자기장의 진폭이 로 감소하는 깊이이다. 파동의 세기는 진폭의 제곱에 비례하므로, 세기가 로 감소하는 깊이는 이다. 도파관에서 유도 전류로 인한 손실은 대부분 표면으로부터 표피 깊이 내에서 발생한다. 따라서 표피 깊이가 얕은 재료로 도파관의 표면을 도금하면 손실이 감소한다.
8. 예시
표피 깊이는 다음 공식을 통해 구할 수 있다.
:
여기서
- 미터 단위의 표피 깊이
- 단위의 감쇠
- 진공의 투자율
- 매질의 상대 투자율 (구리의 경우, = 1.00)
- 매질의 투자율
- Ω·m 단위의 매질의 저항률, 전도도의 역수와 같음: (구리의 경우, ρ = 1.68×10-8Ω·m)
- 매질의 전도율 (구리의 경우, 58.5×106S/m)
- Hz 단위의 전류 주파수
금은 저항률이 2.44×10-8Ω·m인 우수한 도체이며, 비자성체이므로 1이다. 50 Hz 주파수에서 금의 표피 깊이는 11.1 mm이다. 반면 납은 저항률이 2.2×10-7Ω·m로 금보다 약 9배 높다. 따라서 납의 50 Hz 표피 깊이는 약 33 mm로 금의 약 3배이다.

고자성 재료는 투자율 이 커서 표피 깊이가 감소한다. 인덕션 쿠커에 일부 스테인리스강 조리 도구를 사용할 수 없는 이유도 이 때문이다.
10 GHz (마이크로파 영역)와 같이 매우 높은 주파수에서는 좋은 도체의 표피 깊이가 매우 작아진다. 예를 들어, 10 GHz에서 알루미늄, 구리, 금, 은의 표피 깊이는 1 마이크로미터 미만이다.
| 도체 | 표피 깊이 (μm) |
|---|---|
| 알루미늄 | 0.820 |
| 구리 | 0.652 |
| 금 | 0.753 |
| 은 | 0.634 |
마이크로파 주파수에서 대부분의 전류는 표면 근처의 얇은 영역에서 흐르므로, 도파관의 옴 손실은 재료의 표면 코팅에만 의존한다. 3 μm 두께의 은 층은 이러한 주파수에서 우수한 도체 역할을 한다.
구리의 표피 깊이는 주파수의 제곱근에 따라 감소한다.
:
| 주파수 | 표피 깊이 (μm) |
|---|---|
| 50 Hz | 9220 |
| 60 Hz | 8420 |
| 10 kHz | 652 |
| 100 kHz | 206 |
| 1 MHz | 65.2 |
| 10 MHz | 20.6 |
| 100 MHz | 6.52 |
| 1 GHz | 2.06 |
60 Hz에서 반경이 8 mm보다 큰 교류 버스바는 구리의 낭비이며, 대전류 AC용 버스바는 기계적 이유를 제외하고는 12 mm를 넘는 경우가 거의 없다.
9. 비정상 표피 효과
고주파수 및 저온 환경에서는 표피 깊이에 대한 일반적인 공식이 적용되지 않는다. 이 효과는 1940년 하인츠 런던에 의해 처음 발견되었으며, 그는 이 현상이 전자의 평균 자유 행로 길이가 고전적인 표피 깊이 범위에 도달하기 때문이라고 정확하게 제안했다.[24] 매티스-바딘 이론은 금속 및 초전도체에 대한 이 특수한 경우를 위해 개발되었다.
참조
[1]
논문
XIII. On electrical motions in a spherical conductor
1883-01-01
[2]
서적
Standard Handbook for Electrical Engineers
McGraw-Hill
[3]
서적
High-Speed Signal propagation Advanced Black Magic
Prentice Hall
[4]
서적
Engineering Electromagnetics
https://archive.org/[...]
McGraw-Hill
[5]
문서
The formula as shown is algebraically equivalent to the formula found on page 130 {{Harvtxt|Jordan|1968|p=130}}
[6]
문서
Note that the above equation for the current density inside the conductor as a function of depth applies to cases where the usual approximation for skin depth holds. In the extreme cases where it doesn't, the exponential decrease with respect to skin depth still applies to the ''magnitude'' of the induced currents, however the imaginary part of the exponent in that equation, and thus the phase velocity inside the material, are altered with respect to that equation.
[7]
서적
Transmission and Distribution of Electrical Energy
Harper & Row
[8]
문서
"{{harvnb|Terman|1943|p=??}}"
[9]
문서
"{{Harvtxt|Hayt|1981|pp=303}}"
[10]
문서
"{{Harvtxt|Skilling|1951|pp=157–159}}"
[11]
문서
"{{Harvtxt|Hayt|1981|pp=434–439}}"
[12]
문서
"{{Harvtxt|Hayt|1981|p=434}}"
[13]
문서
"{{Harvtxt|Reeve|1995|p=558}}"
[14]
문서
"{{Harvtxt|Chen|2004|p=26}}"
[15]
간행물
Standard Handbook for Electrical Engineers
McGraw Hill
[16]
문서
"{{harvnb|Popovic|Popovic|1999|p=385}}"
[17]
문서
"{{harvnb|Xi Nan|Sullivan|2005}}"
[18]
서적
Modern Power Station Practice
Pergamon Press
[19]
웹사이트
Spinning Carbon Nanotubes Spawns New Wireless Applications
https://www.scienced[...]
Sciencedaily.com
2009-03-09
[20]
논문
Study on Cu/Ni nano superlattice conductors for reduced RF loss
https://www.research[...]
2016-03-16
[21]
문서
"{{Harvtxt|Hayt|1981|pp=401}}"
[22]
문서
"{{harvtxt|Jackson|1999|page=353}}"
[23]
문서
"{{harvtxt|Feynman|1964|page=32-11}}"
[24]
논문
The Anomalous Skin Effect
https://www.jstor.or[...]
1952
[25]
서적
Standard handbook for electrical engineers
https://www.worldcat[...]
McGraw-Hill
2000
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com