맨위로가기

피어폰트 소수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

피어폰트 소수는 2u3v + 1 형태의 소수이다. 이 소수는 무한히 많이 존재하는지 여부는 아직 밝혀지지 않았다. 피어폰트 소수는 106 미만에서 42개, 10100까지 795개가 존재하며, 대수적 인수분해의 제한이 거의 없어 메르센 소수와 같은 조건이 없다. 피어폰트 소수는 프로스 정리를 사용하여 소수성을 검증할 수 있으며, 페르마 수의 인수 탐색 과정에서 발견되기도 한다. 피어폰트 소수는 정다각형 작도와 관련이 있으며, N = 2m3nρ (ρ는 서로 다른 피어폰트 소수의 곱) 형태일 때 컴퍼스, 자, 각 삼등분선으로 N변의 정다각형을 작도할 수 있다. 또한, 2u3v − 1 꼴의 제2종 피어폰트 소수와 일반화된 형태의 소수도 존재한다.

더 읽어볼만한 페이지

  • 수론의 미해결 문제 - 오일러-마스케로니 상수
    오일러-마스케로니 상수 \gamma는 조화급수와 자연로그 함수의 차이의 극한으로 정의되는 수학 상수로, 감마 함수, 리만 제타 함수 등 다양한 수학적 개념과 관련되어 있으며 유리수인지 무리수인지 밝혀지지 않은 미해결 문제이다.
  • 수론의 미해결 문제 - 리만 가설
    리만 가설은 리만 제타 함수의 자명하지 않은 모든 영점의 실수부가 1/2이라는 추측으로, 힐베르트 문제와 클레이 수학 연구소의 밀레니엄 문제 중 하나이며 정수론과 복소해석학을 연결하는 다양한 수학적 명제들과 동치이다.
  • 소수 - 소수 (수론)
    소수는 1과 자기 자신만을 약수로 가지는 1보다 큰 자연수이며, 무한히 많고 정수론의 기본 정리에서 중요한 역할을 하며 다양한 분야에 응용된다.
  • 소수 - 디리클레 L-함수
    디리클레 L-함수는 디리클레 지표로 정의되는 복소함수로, 등차수열에 대한 디리클레 정리를 증명하기 위해 도입되었으며, 리만 제타 함수의 일반화이자 오일러 곱, 함수 방정식 등의 성질을 가지며, 모듈러 형식, 타원 곡선과 관련되어 수론적 L-함수 연구의 핵심이고 암호론, 컴퓨터 과학 등에 응용된다.
피어폰트 소수
수 정보
이름피어폰트 소수
명명 유래제임스 피어폰트
항의 수수천 개
연속성 여부무한
상위 집합피어폰트 수
첫 번째 항2, 3, 5, 7, 13, 17, 19, 37, 73, 97, 109, 163, 193, 257, 433, 487, 577, 769, 1153, 1297, 1459, 2593, 2917, 3457, 3889
가장 큰 알려진 항81 × 220,498,148 + 1
OEISA005109
정의
형태(, > 0)
조건이 3-매끄러운 수 (Smooth number)

2. 분포

작은 피어폰트 소수의 분포. 축은 2의 지수와 3의 지수.


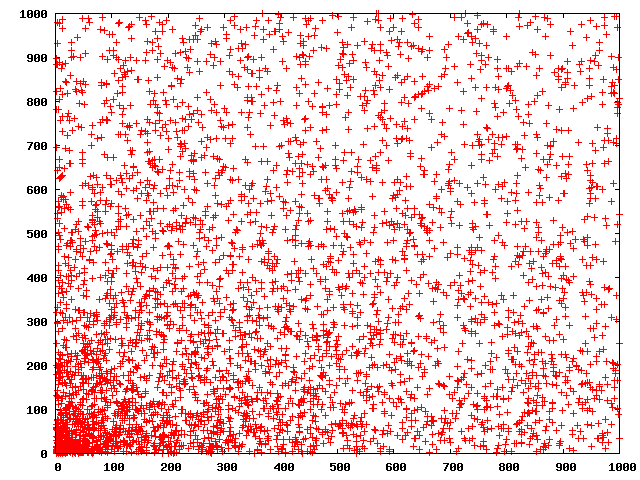
경험적으로 볼 때, 피어폰트 소수는 특별히 희귀하거나 드물게 분포하는 것 같지 않다. 106 미만에는 42개, 109까지는 65개, 1020까지는 157개, 10100까지는 795개의 피어폰트 소수가 존재한다.

피어폰트 소수에는 대수적 인수분해로부터 오는 제약이 거의 없기 때문에, 지수가 소수여야 한다는 메르센 소수의 조건과 같은 특별한 요구 사항은 없다. 따라서 2^u3^v+1 형태의 ''n'' 자릿수 정수 중에서 소수인 것의 비율은, 모든 ''n'' 자릿수 정수 중 소수의 비율과 비슷하게 1/n에 비례할 것으로 예상된다. 이 범위에는 해당 형태의 수가 \Theta(n^2)개 있으므로, \Theta(n)개의 피어폰트 소수가 있을 것으로 추정할 수 있다.

앤드루 M. 글리슨(Andrew M. Gleason)은 이러한 추론을 바탕으로 피어폰트 소수가 무한히 많을 것이라고 추측했다. 더 구체적으로는, 10^n까지 약 9n개의 피어폰트 소수가 존재할 것으로 예상했다.[12] 글리슨의 추측에 따르면, ''N'' 미만의 피어폰트 소수는 \Theta(\log N)개 존재하는 반면, 같은 범위 내의 메르센 소수는 그보다 훨씬 적은 O(\log \log N)개만 존재할 것으로 예상된다.

수학계의 주요 미해결 문제 중 하나는 "피어폰트 소수는 무한히 많이 존재하는가?"이다.

3. 소수 판정법

2^u > 3^v일 때, M=2^u\cdot 3^v + 1 형태의 수는 프로스 수이다. 따라서 이 수가 소수인지 아닌지는 프로스 정리를 이용하여 판정할 수 있다.[2][13]

반면, 2^u < 3^v일 때는 다른 소수 판정법을 사용한다. 이 경우, M=2^u\cdot 3^v + 1에 대해 M-1을 작은 짝수와 큰 3의 거듭제곱의 곱으로 인수분해할 수 있다는 점을 이용한다. 구체적으로는 윌리엄스(Williams)와 자르케(Zarnke)가 개발한 판정법을 사용하는 것이 좋다.[2][13]

4. 페르마 수의 인수로 발견된 피어폰트 소수

지속적인 페르마 수의 인수 탐색 과정에서 일부 피어폰트 소수가 인수로 발견되었다. 다음 표[3]는 페르마 수 F_m = 2^{2^m} + 1을 나누는 피어폰트 소수 p = 3^k \cdot 2^n + 1의 ''m'', ''k'', ''n'' 값과 발견 연도, 발견자를 보여준다.

페르마 수의 인수인 피어폰트 소수
mkn연도발견자
381411903컬렌, 커닝햄 & Western
632671956로빈슨
20712091956로빈슨
45234551956로빈슨
9428294311983켈러
121854121891993더브너
282814282851996타우라
15716711571691995영
21331912133211996영
30308813030931998영
38244713824491999코스그레이브 & 갈로
46107614610812003노하라, Jobling, 월트먼 & 갈로
49572854957322007케이저, Jobling, Penné & 푸게론
67200536720072005쿠퍼, Jobling, 월트먼 & 갈로
2145351121453532003코스그레이브, Jobling, 월트먼 & 갈로
2478782124787852003코스그레이브, Jobling, 월트먼 & 갈로
2543548225435512011브라운, 레이놀즈, Penné & 푸게론


5. 정다각형 작도

종이접기 수학에서 후지타-하토리 공리는 삼차 방정식을 풀 수 있는 점의 작도를 가능하게 한다.[5][15] 이를 통해, 변의 개수 N이 3 이상이고 N = 2m3nρ (m, n ≥ 0, ρ는 서로 다른 피어폰트 소수의 곱) 형태일 때, 정N각형을 종이접기로 만들 수 있다는 결론을 얻을 수 있다.[16] 이는 컴퍼스, 자, 그리고 각의 삼등분선을 사용하여 작도할 수 있는 정다각형의 종류와 동일하다.[1]

컴퍼스와 자만으로 작도할 수 있는 정다각형(작도 가능한 다각형)은 위 조건에서 n=0이고 ρ가 서로 다른 페르마 소수의 곱인 특수한 경우이다. 페르마 소수는 피어폰트 소수의 부분집합이다.[16]

1895년, 제임스 피어폰트는 원뿔 곡선을 이용한 작도 가능성을 연구하며 동일한 종류의 정다각형을 다루었다. 피어폰트 소수라는 이름은 그의 연구에서 유래했다. 피어폰트는 컴퍼스와 자 작도에 더해, 이미 작도된 점들의 좌표를 계수로 가지는 원뿔 곡선을 그릴 수 있는 능력을 추가하는 방식으로 작도법을 일반화했다. 그가 보인 바에 따르면, 이러한 연산으로 작도할 수 있는 정N각형은 N의 오일러 피 함수 φ(N)이 3-smooth한(즉, 소인수가 2와 3뿐인) 경우이다.[6][17] 소수 N의 경우, φ(N) = N-1이므로, 피어폰트의 작도법이 적용되는 소수 각형의 변의 수 N은 정확히 피어폰트 소수가 된다. 그러나 피어폰트는 φ(N)이 3-smooth한 합성수 N의 형태를 명확히 밝히지는 않았다.[6][17] 이후 앤드루 글리슨(Andrew Gleason)이 이러한 합성수를 포함한 모든 N이 앞서 언급한 N = 2m3nρ 형태임을 증명했다.[1][17]

피어폰트 소수가 아닌 가장 작은 소수는 11이다. 따라서 십일각형은 컴퍼스, 자, 각의 삼등분기(또는 종이접기, 원뿔 곡선)를 이용하여 작도할 수 없는 가장 작은 정다각형이다.[1] 3 ≤ N ≤ 21 범위의 다른 모든 정N각형은 이 방법들로 작도할 수 있다.[1]

6. 일반화

'''제2종 피어폰트 소수'''는 2''u''3''v'' − 1 꼴의 소수이다. 이 수들은 다음과 같다.

: 2, 3, 5, 7, 11, 17, 23, 31, 47, 53, 71, 107, 127, 191, 383, 431, 647, 863, 971, 1151, 2591, 4373, 6143, 6911, 8191, 8747, 13121, 15551, 23327, 27647, 62207, 73727, 131071, 139967, 165887, 294911, 314927, 442367, 472391, 497663, 524287, 786431, 995327, ... (OEIS의 수열 A005105)

이 유형의 가장 큰 알려진 소수는 메르센 소수이다. 현재 가장 큰 알려진 메르센 소수는 2^{136279841}-1 (십진수 41,024,320자리)이다. 메르센 소수가 아닌 제2종 피어폰트 소수 중 가장 큰 알려진 소수는 PrimeGrid에서 찾은 3\cdot 2^{22103376}-1이다.[7]

'''일반화된 피어폰트 소수'''는 ''k''개의 고정된 소수 ''p''1 < ''p''2 < ''p''3 < ... < ''p''''k''에 대해 p_1^{n_1} \!\cdot p_2^{n_2} \!\cdot p_3^{n_3} \!\cdot \ldots \cdot p_k^{n_k} + 1 꼴의 소수이다. '''제2종 일반화된 피어폰트 소수'''는 ''k''개의 고정된 소수 ''p''1 < ''p''2 < ''p''3 < ... < ''p''''k''에 대해 p_1^{n_1} \!\cdot p_2^{n_2} \!\cdot p_3^{n_3} \!\cdot \ldots \cdot p_k^{n_k} - 1 꼴의 소수이다. 2보다 큰 모든 소수는 홀수이므로, 두 종류 모두에서 ''p''1은 2여야 한다. 이러한 소수들의 수열은 OEIS에 다음과 같이 나타나 있다.

{p1, p2, p3, ..., pk}+ 1− 1
{2}(OEIS의 수열 A092506)(OEIS의 수열 A000668)
{2, 3}(OEIS의 수열 A005109)(OEIS의 수열 A005105)
{2, 5}(OEIS의 수열 A077497)(OEIS의 수열 A077313)
{2, 3, 5}(OEIS의 수열 A002200)(OEIS의 수열 A293194)
{2, 7}(OEIS의 수열 A077498)(OEIS의 수열 A077314)
{2, 3, 5, 7}(OEIS의 수열 A174144)(OEIS의 수열 A347977)
{2, 11}(OEIS의 수열 A077499)(OEIS의 수열 A077315)
{2, 13}(OEIS의 수열 A173236)(OEIS의 수열 A173062)


참조

[1] 간행물 Angle trisection, the heptagon, and the triskaidecagon
[2] 간행물 On the primality of 2h\cdot 3^n+1
[3] 웹사이트 Fermat factoring status http://www.prothsear[...] Wilfrid Keller
[4] 웹사이트 The largest known primes http://primes.utm.ed[...] 2023-06-17
[4] 웹사이트 The Prime Database: 81*2^20498148+1 https://primes.utm.e[...] 2023-06-17
[5] 간행물 Solving cubics with creases: the work of Beloch and Lill
[6] 간행물 On an undemonstrated theorem of the Disquisitiones Arithmeticæ
[7] 웹사이트 3*2^22103376 - 1 https://primes.utm.e[...]
[8] 서적 ガロワ理論 日本評論社
[9] 문서 3以下の素因数しか持たないこと。
[10] 웹사이트 The largest known primes http://primes.utm.ed[...] 2021-01-02
[11] 웹사이트 The Prime Database: 3*2^16408818+1 https://primes.utm.e[...] 2021-01-02
[12] 간행물 Angle trisection, the heptagon, and the triskaidecagon
[13] 간행물 On the primality of 2h\cdot 3^n+1
[14] 웹사이트 Fermat factoring status http://www.prothsear[...] Wilfrid Keller
[15] 간행물 Solving cubics with creases: the work of Beloch and Lill
[16] 문서 0個の数の積すなわち ρ=1 でもよいとする。空積を参照せよ。
[17] 간행물 On an undemonstrated theorem of the Disquisitiones Arithmeticæ


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com