십일각형

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정십일각형
3. 십일각형의 활용
- 3.1. 외국의 사례
4. 관련 도형
참조

1. 개요

십일각형은 11개의 변과 꼭짓점을 가진 다각형을 의미한다. 정십일각형은 모든 변의 길이와 각의 크기가 같으며, 슐래플리 기호 {11}로 나타낸다. 정십일각형의 내각은 약 147.27도이고, 중심각과 외각은 약 32.72도이다. 자와 컴퍼스로 작도할 수는 없지만, 근사값을 작도하거나 뉴시스 작도 및 종이 접기를 통해 작도할 수 있다. 십일각형은 캐나다 1달러 주화(루니) 및 인도 2루피 주화 등에서 활용되며, 관련 도형으로는 4개의 정규 십일각성이 있다.

더 읽어볼만한 페이지

11 - 십일진법
십일진법은 11을 밑으로 하는 위치 기수법으로, 0부터 9까지의 아라비아 숫자와 10을 나타내는 기호 A를 사용하여 숫자를 표현하며, 컴퓨터 과학, ISBN 검증, 일부 대중문화 작품 등에서 활용된다.
11 - 11-11-11
11-11-11은 2011년 개봉한 미국의 공포 영화로, 아내와 아들을 잃고 신에 대한 믿음을 잃은 작가가 초자연적인 현상을 겪으며 악마의 부활을 막는 과정을 다룬다.
변의 수에 따른 다각형 - 오각형
다섯 변으로 이루어진 다각형인 오각형은 변의 길이와 각의 크기가 모두 같은 정오각형을 포함하며, 정오각형은 컴퍼스와 자로 작도할 수 있고 자연에서도 발견된다.
변의 수에 따른 다각형 - 육각형
육각형은 여섯 변과 꼭짓점으로 이루어진 다각형으로, 특히 모든 변과 각이 같은 정육각형은 평면 테셀레이션이 가능하고 벌집 구조, 건축, 자연 현상, 한국 전통 문양 등 다양한 분야에서 활용된다.

십일각형
개요
이름	십일각형
영어 이름	Hendecagon, Undecagon
변의 수	11
각의 수	11
슈플리 기호	{11}
정십일각형
내각의 크기	147.272727...°
특징	작도 불가능 (자, 컴퍼스)
기타
관련 항목	다각형

2. 정십일각형

정십일각형은 모든 변의 길이와 각의 크기가 같은 십일각형으로, 슐래플리 기호는 {11}이다.

정십일각형은 자와 눈금 없는 자 및 컴퍼스로는 작도할 수 없다.^[6] 다만, 고대 그리스 수학자들은 단위 원에 내접하는 십일각형의 변의 길이를 14/25 단위로 근사했다.^[7]

2. 1. 기하학적 성질

정십일각형의 내각은 147.27 도(=147

\tfrac{3}{11}

도)이다.^[4] 중심각과 외각은 32.72…°이다.^[15] 변의 길이가 ''a''인 정십일각형의 면적은 다음과 같다.^[5]

:

A = \frac{11}{4}a^2 \cot \frac{\pi}{11} \simeq 9.36564\,a^2.

11은 페르마 소수가 아니므로, 정십일각형은 자와 눈금 없는 자 및 컴퍼스로 작도할 수 없다.^[6] 11은 피어폰트 소수가 아니기 때문에, 각 삼등분기를 사용하더라도 정십일각형을 작도할 수 없다.

하지만, 뉴시스 작도를 통해 정십일각형을 정확하게 작도할 수 있으며,^[8] 두 번 접는 종이 접기를 통해서도 작도할 수 있다.^[9]

\cos (2\pi/11)

의 값은 멱근을 사용하여 다음과 같이 나타낼 수 있다.^[15]

:

\begin{align}\cos \frac{2\pi}{11} =& -\frac{1}{10}\\&+\frac{-1+\sqrt{5}+i\sqrt{10+2\sqrt{5}}}{40}\left \lbrace \sqrt[5]{-\frac{11}{4}\left \lbrace 89+25\sqrt{5}+\left (45\sqrt{5-2\sqrt{5}}-5\sqrt{5+2\sqrt{5}} \right )i \right \rbrace }  + \sqrt[5]{-\frac{11}{4}\left \lbrace 89-25\sqrt{5}+\left (5\sqrt{5-2\sqrt{5}}+45\sqrt{5+2\sqrt{5}} \right )i \right \rbrace} \right \rbrace \\&+\frac{-1+\sqrt{5}-i\sqrt{10+2\sqrt{5}}}{40}\left \lbrace \sqrt[5]{-\frac{11}{4}\left \lbrace 89+25\sqrt{5}-\left (45\sqrt{5-2\sqrt{5}}-5\sqrt{5+2\sqrt{5}} \right )i \right \rbrace }  + \sqrt[5]{-\frac{11}{4}\left \lbrace 89-25\sqrt{5}-\left (5\sqrt{5-2\sqrt{5}}+45\sqrt{5+2\sqrt{5}} \right )i \right \rbrace} \right \rbrace \\=& 0.841253\dots\end{align}

2. 2. 작도 불가능성

11은 페르마 소수가 아니므로, 정십일각형은 자와 눈금 없는 자와 컴퍼스로 작도할 수 없다.^[6] 11은 피어폰트 소수가 아니기 때문에, 각 삼등분기를 사용하더라도 정십일각형을 작도할 수 없다.

그러나 뉴시스 작도를 사용하면 정십일각형을 정확하게 작도할 수 있으며,^[8] 두 번 접는 종이 접기를 통해서도 작도할 수 있다.^[9]

2. 3. 근사적 작도

고대 그리스 수학자들은 단위 원에 내접하는 십일각형의 변의 길이를 14/25 단위로 근사했다. 1800년 T. Drummond는 십일각형의 근사적 작도법을 제시했다.^[10] 이 방법은 단위 원의 반지름이 10m일 때 약 2.3mm의 오차를 가진다.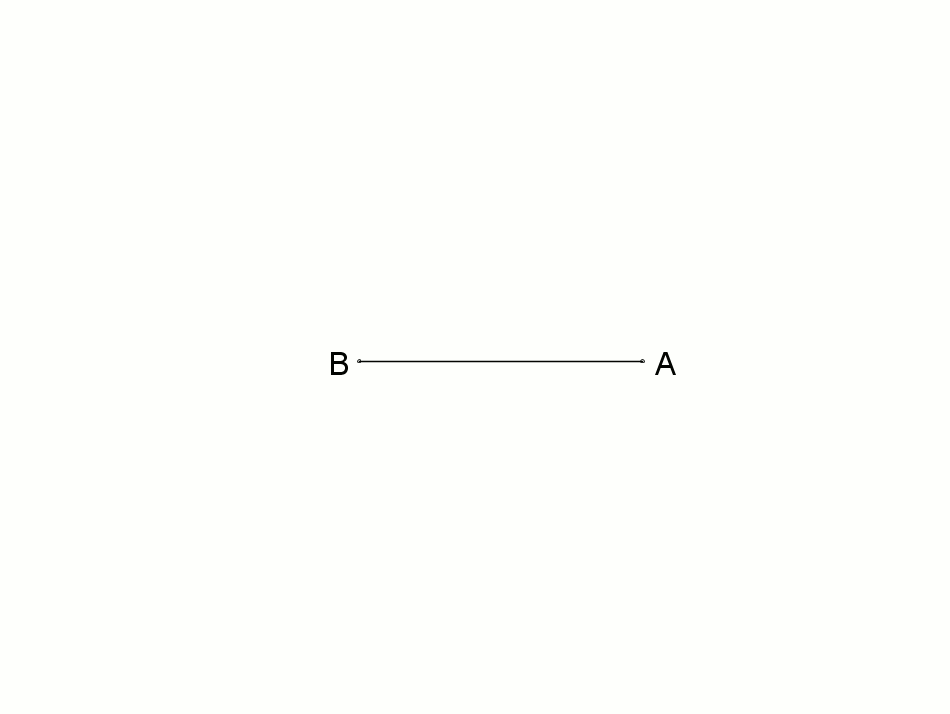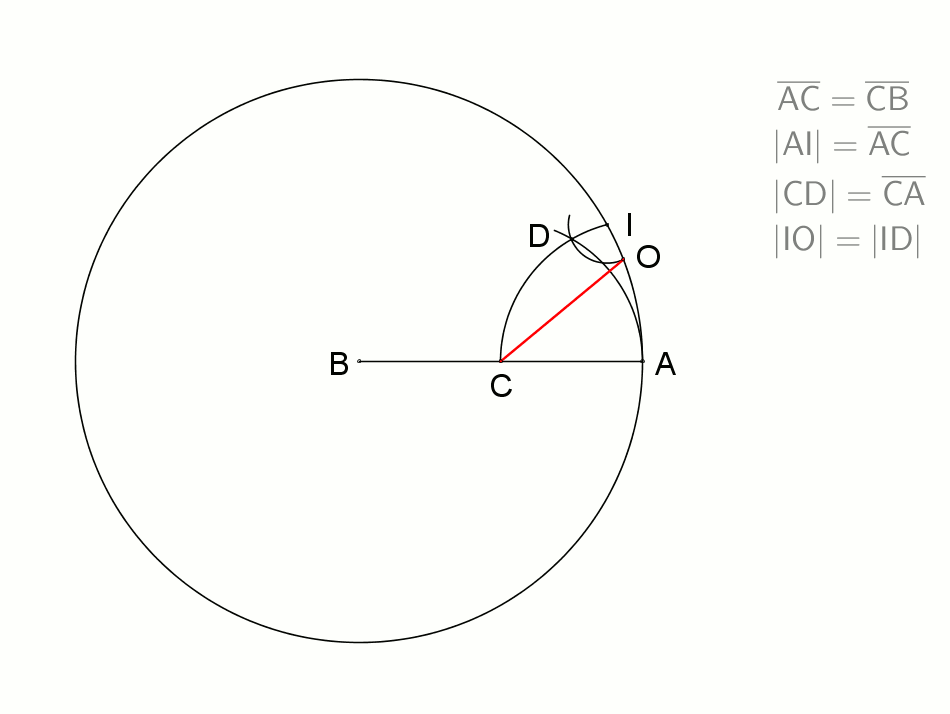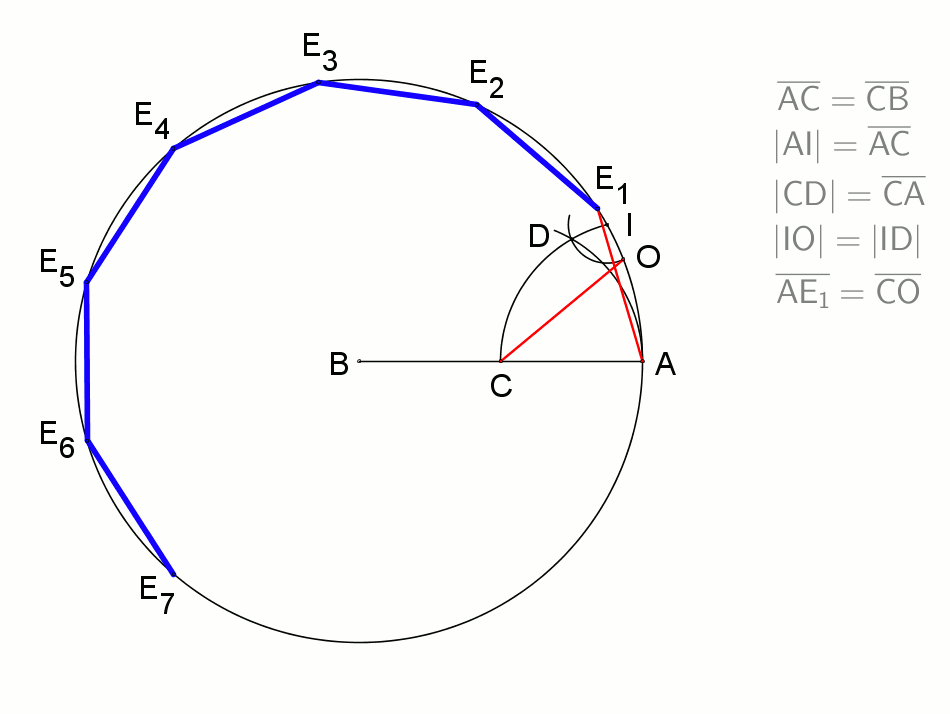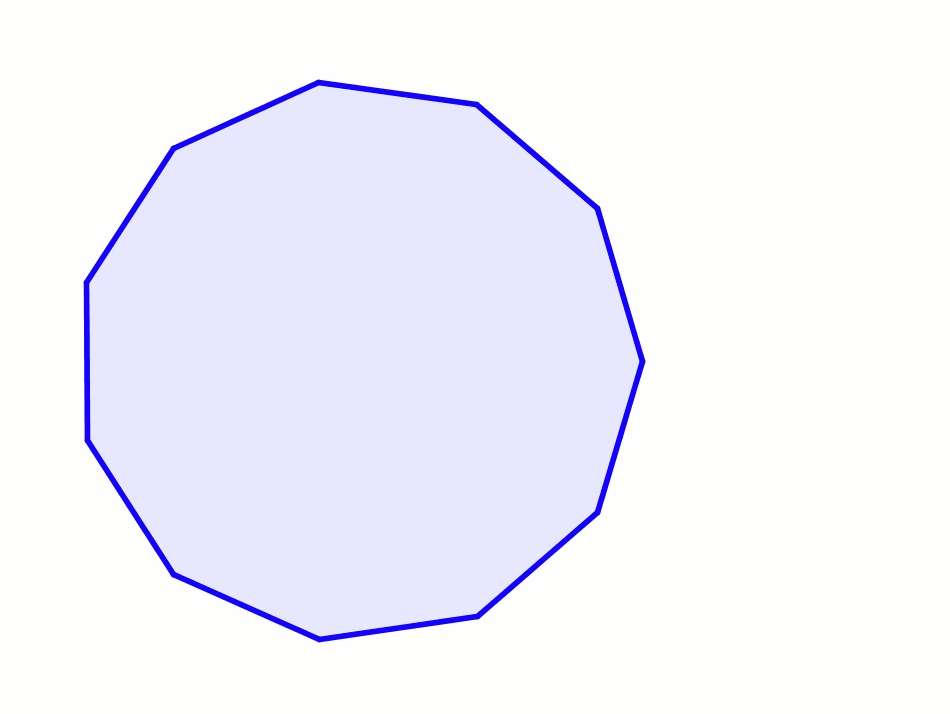

T. Drummond가 제시한 기본 작도의 연속(애니메이션). Anton Ernst Burkhard of Birckenstein의 구리 조각과 일치한다.

다음은 1800년 T. Drummond가 제시한 작도 방법이다.^[10]

반지름 '''A B'''를 그리고, '''C'''에서 이등분한다. 컴퍼스의 열린 간격을 반지름의 절반으로 하여 '''A'''와 '''C'''를 중심으로 '''C D I'''와 '''A D''' 호를 그린다. 거리 '''I D'''를 이용하여 '''I'''에서 호 '''D O'''를 그리고 '''C O'''선을 그린다. 이 선은 실용적으로 충분히 정확한 십일각형의 한 변의 길이이다.

단위 원에서:

작도된 십일각형 변의 길이: $b=0.563692\ldots$
이론적인 십일각형 변의 길이: $a=2\sin(\frac{\pi}{11})=0.563465\ldots$
절대 오차: $\delta=b-a=2.27\ldots\cdot10^{-4}$ – 만약 가 10m라면 이 오차는 약 2.3 mm이다.

2. 4. 대칭성

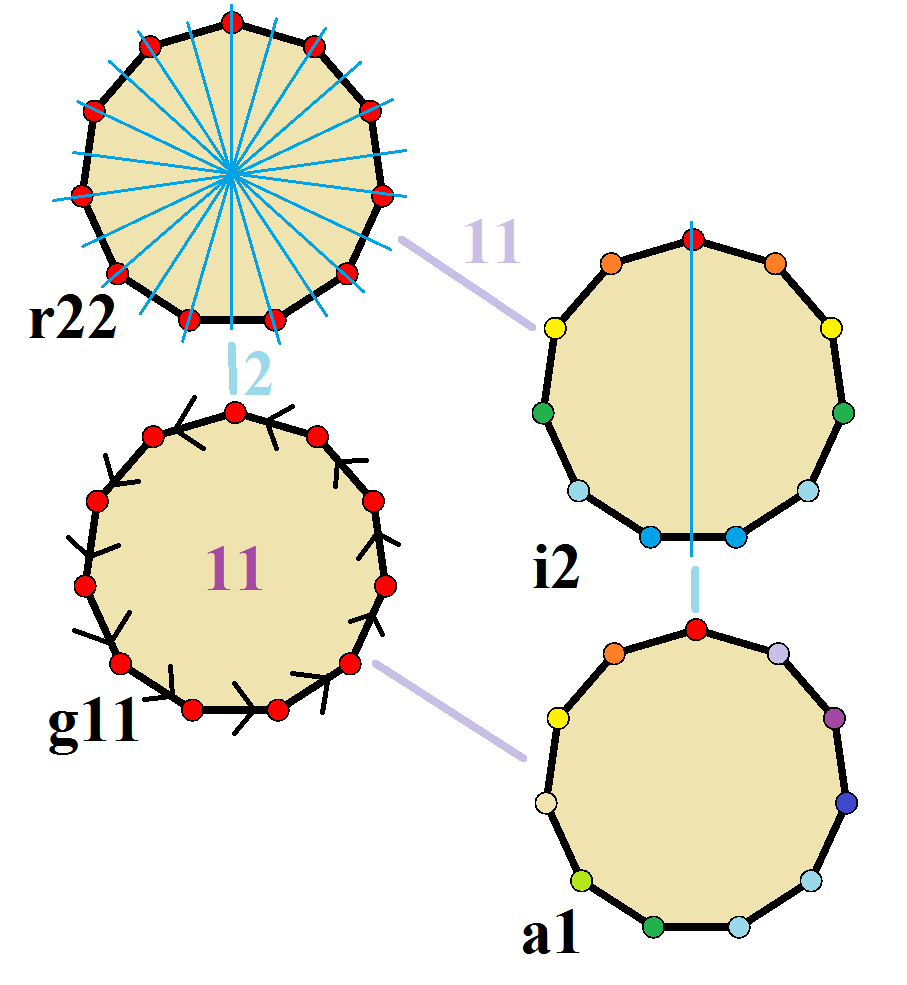
정십일각형의 대칭. 꼭짓점은 대칭 위치에 따라 색상이 지정되어 있다. 파란색 거울 선은 꼭짓점과 변을 통과하여 그려진다. 회전 차수는 중앙에 표시되어 있다.

정십일각형은 Dih₁₁ 대칭(차수 22)을 갖는다. 11은 소수이므로, 이면각 대칭을 갖는 부분군 하나(Dih₁)와 순환군 대칭 두 개(Z₁₁, Z₁)가 존재한다.

이 4개의 대칭은 십일각형에서 4개의 뚜렷한 대칭으로 볼 수 있다. 존 콘웨이는 이러한 대칭을 문자와 군의 차수를 사용하여 표기했다.^[11] 정규 형태의 전체 대칭은 '''r22'''이고, 대칭이 없는 것은 '''a1'''으로 표시된다. 이면각 대칭은 꼭짓점을 통과하는지('''d''', 대각선), 변을 통과하는지('''p''', 수직)에 따라 구분되며, 반사선이 변과 꼭짓점 모두를 통과하는 경우 '''i'''로 표시된다. 가운데 열의 순환 대칭은 중심 회전 차수에 따라 '''g'''로 표시된다.

각 부분군 대칭은 불규칙한 형태에 대해 하나 이상의 자유도를 허용한다. '''g11''' 부분군만이 자유도가 없지만, 유향 변으로 볼 수 있다.

3. 십일각형의 활용

십일각형은 주화 디자인에 활용된 사례가 있다. 캐나다의 1달러 주화(루니)와 미국의 1달러 주화, 인도의 2루피 주화가 그 예이다.

3. 1. 외국의 사례

캐나다 1달러 주화(루니)는 정십일각형 모양과 유사하지만, 엄밀하게는 뢸로 십일각형이다.^[12] 인도 2루피 주화에도 십일각형 디자인이 사용되었다.^[13] 미국의 수잔 B. 앤서니 달러 주화는 가장자리 내부에 십일각형 윤곽을 가지고 있다.

4. 관련 도형

십일각형은 4개의 정규 십일각성과 동일한 11개의 꼭짓점을 공유한다.

{11/2}

{11/3}

{11/4}

{11/5}

참조

_[1] 간행물 Construction of the regular undecagon by a sextic curve
_[2] 서적 Errors of speech and of spelling https://archive.org/[...] W. Tegg and co.
_[3] 웹사이트 Hendecagon – from Wolfram MathWorld http://mathworld.wol[...]
_[4] 서적 Glencoe mathematics: applications and connections https://archive.org/[...] Glencoe/McGraw-Hill
_[5] 서적 Elements of Plane and Spherical Trigonometry: With Their Applications to Mensuration, Surveying, and Navigation https://archive.org/[...] Harper
_[6] 서적 Mathematical Thought From Ancient to Modern Times https://books.google[...] Oxford University Press
_[7] 서적 A History of Greek Mathematics, Vol. II: From Aristarchus to Diophantus https://archive.org/[...] The Clarendon Press
_[8] 논문 https://dx.doi.org/1[...] 2014-05
_[9] 논문 Construction of a regular hendecagon by two-fold origami https://cms.math.ca/[...] 2018-06-20
_[10] 서적 The Young Ladies and Gentlemen's AUXILIARY, in Taking Heights and Distances ... https://books.google[...] 1800
_[11] 서적 The Symmetries of Things 2008
_[12] 간행물 A $1 problem http://www.maa.org/s[...]
_[13] 서적 2013 Standard Catalog of World Coins 2001 to Date https://books.google[...] Krause Publications
_[14] 서적 Unusual World Coins Krause Publications
_[15] 블로그 cos(2π/11) を冪根で求めようとしたらとんでもないことになった(2/11,3/10追加) | てっぃちMarshの数学（Mathematics)教室 https://ameblo.jp/ti[...]
_[16] 논문 On the construction of the regular hendecagon by marked ruler and compass Cambridge University Press
_[17] 논문 Construction of a regular hendecagon by two-fold origami https://cms.math.ca/[...] 2018

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com