해시 테이블

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

해시 테이블은 키를 해시 함수를 통해 배열 인덱스로 변환하여 데이터를 저장하고 검색하는 자료구조이다. 1953년 H. P. Luhn에 의해 처음 사용되었으며, 충돌 해결을 위해 분리 연결법과 개방 주소법을 사용한다. 해시 함수는 해시 테이블의 성능에 중요한 영향을 미치며, 균등 분포를 유지하는 것이 중요하다. 해시 테이블은 동적 크기 조정을 통해 부하율을 관리하며, 재해싱을 통해 테이블 크기를 조정한다. 다양한 프로그래밍 언어에서 연관 배열, 캐시, 집합 등을 구현하는 데 사용되며, C++, Java, Python, JavaScript 등에서 내장된 형태로 제공된다.

더 읽어볼만한 페이지

해싱 - 해시 충돌
해시 충돌은 해시 함수에서 서로 다른 입력값이 동일한 해시값을 생성하는 현상으로, 데이터 수와 해시 값 범위에 따라 발생 가능성이 높아지며 데이터 무결성 및 보안 상의 문제점을 야기하여 해결 방법이 연구되고 있다.
해싱 - HMAC
HMAC(Keyed-Hash Message Authentication Code)는 공유된 비밀 키와 암호화 해시 함수를 사용하여 메시지의 무결성을 검증하는 메시지 인증 코드로서, IPsec, SSH, TLS, JSON 웹 토큰 등 다양한 보안 프로토콜에서 활용된다.
배열 - 원형 버퍼
원형 버퍼는 고정 크기의 자료구조로, 처음과 끝이 연결되어 데이터가 순환하며 저장되는 FIFO 방식의 버퍼이며, 큐 구현, 멀티미디어 스트리밍, 데이터 압축 등에 활용된다.
배열 - 할바흐 배열
할바흐 배열은 특정 면에 자기장을 집중시키고 다른 면에서는 상쇄시키는 배열로, 자장 격리에 유용하며 다양한 산업 및 첨단 기술 분야에 응용된다.

해시 테이블
개요
유형	연관 배열
고안자	아서 새뮤얼 진 아므달 일레인 맥고원
고안 연도	1953년
성능
공간 (평균)	Θ(n)
공간 (최악)	O(n)
검색 (평균)	Θ(1)
검색 (최악)	O(n)
삽입 (평균)	Θ(1)
삽입 (최악)	O(n)
삭제 (평균)	Θ(1)
삭제 (최악)	O(n)
일반 정보
다른 이름	해시 맵 맵 딕셔너리 연관 배열

2. 역사

해시의 개념은 여러 곳에서 독립적으로 발생하였다. 1953년 1월, 한스 피터 룬은 체이닝을 사용한 해싱에 대한 IBM 내부 메모를 작성했다.^[60] 거의 같은 시기에 진 암달, 일레인 M. 맥그로우, 내서니얼 로체스터, 아서 사무엘은 해싱을 사용하는 프로그램을 제공하였다.^[60]

오픈 어드레싱의 첫 번째 예시는 룬의 메모를 기반으로 A. D. 린이 제안했다.^[4] 암달은 선형 탐사를 사용한 오픈 어드레싱의 공로자로 여겨지지만, 안드레이 예르쇼프도 독립적으로 같은 아이디어를 냈다.^[6] W. 웨슬리 피터슨의 논문에서 "오픈 어드레싱"이라는 용어가 처음 사용되었다.^[7]

아놀드 더미는 소수를 모듈로 하는 나머지를 해시 함수로 사용하는 아이디어를 논의하며, 체이닝을 사용한 해싱에 대한 첫 번째 학술 출판물을 냈다. "해싱"이라는 단어는 로버트 모리스의 논문에서 처음 출판되었다. 콘하임과 와이스는 선형 탐사의 알고리즘 분석에 대한 이론적 분석을 처음으로 제출하였다.

2. 1. 한국의 해시 기술 발전

''적재율''

\alpha

은 해시 테이블의 중요한 통계치이며 다음과 같이 정의된다.^[1]

\text{적재율}\ (\alpha) = \frac{n}{m},

여기서

$n$ 은 해시 테이블에 채워진 항목의 수이다.
$m$ 은 버킷의 수이다.

해시 테이블의 성능은 적재율

\alpha

에 따라 저하된다.

소프트웨어는 일반적으로 양호한 성능을 유지하기 위해 적재율

\alpha

가 특정 상수

\alpha_{\max}

이하로 유지되도록 한다. 따라서 적재율

\alpha

가

\alpha_{\max}

에 도달할 때마다 해시 테이블의 크기를 조정하거나 "재해싱"하는 것이 일반적인 접근 방식이다. 마찬가지로 적재율이

\alpha_{\max}/4

이하로 떨어지는 경우에도 테이블의 크기를 조정할 수 있다.^[8]

3. 해시 함수

해시 함수는 해시 테이블에서 키를 기반으로 생성된 해시 값을 인덱스로 사용하는 배열이다. 일반적으로 배열의 인덱스에는 음이 아닌 정수만 사용할 수 있다. 따라서 키를 요약한 값인 해시 값을 인덱스로 사용하여 값을 관리함으로써, 검색 및 추가 작업을 요소 수에 관계없이 상수 시간 ''O''(1)으로 구현한다. 그러나 해시 함수 선택에 따라 성능이 저하되어 최악의 경우 ''O''(n)이 될 수 있다.

해시 값의 균등 분포는 해시 함수의 기본적인 요구 사항이다. 균등하지 않은 분포는 충돌 횟수를 증가시키고 이를 해결하는 비용을 증가시킨다. 균등성은 설계를 통해 보장하기 어려울 때도 있지만, 통계적 검정을 사용하여 경험적으로 평가할 수 있다. 예를 들어, 이산 균등 분포에 대한 피어슨 카이 제곱 검정이 있다.^[14]^[15]

분포는 응용 프로그램에서 발생하는 테이블 크기에 대해서만 균등하면 된다. 특히 테이블 크기를 정확하게 두 배로 늘리거나 줄이는 동적 크기 조정을 사용하는 경우, 해시 함수는 크기가 2의 거듭제곱일 때만 균등해야 한다. 여기서 인덱스는 해시 함수의 비트 범위로 계산할 수 있다. 반면에 일부 해싱 알고리즘은 크기가 소수인 것을 선호한다.^[16]

오픈 어드레싱 방식의 경우, 해시 함수는 두 개 이상의 키를 연속적인 슬롯에 매핑하는 ''클러스터링''도 피해야 한다. 이러한 클러스터링은 적재율이 낮고 충돌이 드물더라도 조회 비용을 급증시킬 수 있다. 널리 사용되는 곱셈 해시는 특히 클러스터링 동작이 좋지 않다고 알려져 있다.^[16]^[4]

K-독립 해싱은 주어진 유형의 해시 테이블에 대해 특정 해시 함수가 나쁜 키 집합을 갖지 않음을 증명하는 방법을 제공한다. 선형 탐사 및 뻐꾸기 해싱과 같은 충돌 해결 방식에 대해 여러 K-독립성 결과가 알려져 있다. K-독립성은 해시 함수가 작동함을 증명할 수 있으므로, 가능한 가장 빠른 해시 함수를 찾는 데 집중할 수 있다.^[17]

3. 1. 정수 해싱

해시 함수

h : U \rightarrow \{0, ..., m-1\}

는 키의 전체 집합

U

를 테이블 내의 인덱스 또는 슬롯으로 매핑한다. 즉,

h(x) \in \{0, ..., m-1\}

이며

x \in U

이다. 해시 함수의 일반적인 구현은 테이블의 모든 요소가 전체 집합

U = \{0, ..., u - 1\}

에서 유래한다는 ''정수 전체 집합 가정''에 기반하며, 여기서

u

의 비트 길이는 컴퓨터 아키텍처의 워드 크기 내로 제한된다.

완전 해시 함수는 주어진 집합

S

에 대해 해시 함수

h

가 단사 함수인 경우를 말한다. 즉, 각 요소

x \in S

가

{0, ..., m-1}

에서 다른 값으로 매핑된다. 완전 해시 함수는 모든 키가 미리 알려져 있는 경우 생성할 수 있다.

''정수 유니버스 가정''에서 사용되는 해싱 기법에는 나눗셈 해싱, 곱셈 해싱, 유니버설 해싱, 동적 완전 해싱, 정적 완전 해싱이 있다.^[13]

3. 1. 1. 나눗셈 해싱

''정수 유니버스 가정''에서 사용되는 해싱 기법에는 나눗셈 해싱, 곱셈 해싱, 유니버설 해싱, 동적 완전 해싱, 정적 완전 해싱이 있다.^[13] 하지만, 나눗셈 해싱이 일반적으로 사용되는 기법이다.^[13]

해시 테이블에서 나누기 방식은 다음과 같다.^[13]

:

h(x)\ =\ x\, \bmod\, m

여기서

h(x)

는

x \in S

의 해시 값이고,

m

은 테이블의 크기이다.

3. 1. 2. 곱셈 해싱

곱셈 해싱 방식은 다음과 같다.

:

h(x) = \lfloor m \bigl((xA) \bmod 1\bigr) \rfloor

여기서

A

는 정수가 아닌 실수 상수이고,

m

은 테이블의 크기이다. 곱셈 해싱의 장점은

m

이 중요하지 않다는 것이다.^[13] 어떤 값

A

라도 해시 함수를 생성하지만, 도널드 커누스는 황금비율을 사용할 것을 제안한다.^[13]

4. 충돌 해결

해싱을 사용하는 탐색 알고리즘은 해시 함수 계산과 충돌 해결 두 부분으로 구성된다. 해시 함수는 탐색 키를 배열 인덱스로 변환하며, 이상적인 경우 서로 다른 두 탐색 키가 동일한 배열 인덱스로 해싱되지 않지만, 현실적으로 이는 불가능하다.^[18] 따라서 충돌 해결이 필요하며, 일반적인 방법으로 분리 연결법과 개방 주소법이 있다.^[19]

여러 키가 같은 해시값을 가지는 것을 '''충돌'''(collision)이라 하며, 키 분포를 미리 알 수 없는 경우 충돌을 피할 수 없다. 충돌 발생 시 대처 방법으로는 개방 주소법과 분리 연결법(체이닝)이 있다.

분리 연결법은 각 버킷에 연결 리스트를 사용하여 충돌을 해결하고, 개방 주소법은 버킷 배열 내에서 탐사를 통해 충돌을 해결한다. 분리 연결법은 적재율이 높아져도 성능 저하가 점진적인 반면, 개방 주소법은 적재율이 1에 가까워질수록 성능이 급격히 저하된다.^[8]

4. 1. 분리 연결법 (Separate Chaining)

분리 연결법(Separate Chaining)은 해시 충돌을 해결하는 한 가지 방법으로, 연쇄법(chaining)이라고도 한다. 이 방법은 동일한 해시 값을 갖는 키들을 링크드 리스트에 저장하는 방식이다.

분리 연결 해시 테이블에서 각 버킷(bucket)은 데이터 목록 또는 배열에 대한 포인터를 저장한다.^[9] 충돌이 발생하면, 해당 버킷의 링크드 리스트에 새로운 키-값 쌍을 추가한다.

일반적으로 크기가 ''N''인 루트 배열을 만들고, 각 루트 배열 요소에 엔트리 리스트(링크드 리스트)를 저장한다. 엔트리를 저장할 때, 해시 함수를 사용하여 키로부터 해시 값을 계산한다. (해시 함수는 0부터 ''N'' - 1 사이의 정수 값을 균일하게 분포시키고 빠르게 계산할 수 있어야 한다.) 해시 값을 ''i''라고 하면, 루트 배열의 ''i''번째 엔트리 리스트에 엔트리를 저장한다. 만약 다른 키가 동일한 해시 값을 가지면(충돌), 같은 엔트리 리스트에 추가한다. 검색 시에는 키를 해시 값으로 변환하여 해당 버킷의 링크드 리스트에서 일치하는 키를 찾는다.

분리 연결법은 적재율(로드 팩터)이 높아져도 성능이 급격히 나빠지지 않고 점진적으로 저하된다.^[8] 일반적으로 분리 연결에서 최상의 성능을 제공하는 최대 적재율(

\alpha_{\max}

) 값은 1과 3 사이이다.^[8]

(하위 섹션의 내용과 중복되어 간략하게 수정)

4. 1. 1. 분리 연결법의 장점

분리 연결(Separate Chaining)은 각 검색 배열 인덱스에 키-값 쌍으로 연결 리스트를 구축한다. 충돌된 항목들은 단일 연결 리스트를 통해 함께 연결되며, 고유한 검색 키를 가진 항목에 접근하기 위해 탐색할 수 있다.^[20] 연결 리스트를 이용한 체이닝은 해시 테이블의 일반적인 구현 방법이다.

키가 정렬되어 있다면, 자기 구성 개념(예: 균형 이진 탐색 트리)을 사용하여 이론적 최악의 경우를

O(\log{n})

으로 줄일 수 있다. (단, 추가적인 복잡성이 있다.)

동적 완전 해싱은 2단계 해시 테이블을 사용하여 검색 복잡도를 최악의 경우

O(1)

로 보장한다. 이 기술에서

k

개의 항목을 가진 버킷은

k^2

개의 슬롯을 가진 완전 해시 테이블로 구성되어, 최악의 경우 상수 시간 검색 및 낮은 상환 삽입 시간을 제공한다.^[21]

융합 트리를 각 버킷에 사용하는 기술은 높은 확률로 모든 연산에 대해 상수 시간을 제공한다.^[22] 분리 연결 구현에서 연결 리스트의 노드가 메모리 전체에 흩어져 있으면 공간 지역성(참조 지역성) 때문에 캐시를 고려하지 않을 수 있다. 따라서 삽입 및 검색 중 리스트 순회는 CPU 캐시 비효율성을 초래할 수 있다.^[23]

캐시를 고려하는 분리 연결 충돌 해결 방법에서는 연결 리스트나 자체 균형 이진 탐색 트리 대신 동적 배열이 캐시 친화적인 것으로 나타났다. 이는 배열의 연속 할당 패턴이 하드웨어 캐시 프리페처(예: TLB)에 의해 활용되어 접근 시간과 메모리 소비를 줄이기 때문이다.^[24]^[25]^[26]

4. 1. 2. 분리 연결법의 단점

분리 연결 해시 테이블은 적재율(로드 팩터)이 증가함에 따라 성능이 점진적으로 저하된다.^[8] 각 버킷에 연결 리스트를 사용하는 경우, 노드들이 메모리 전체에 흩어져 있으면 참조 지역성이 떨어져 CPU 캐시 비효율성을 초래할 수 있다.^[23] 이러한 문제를 해결하기 위해 연결 리스트 대신 동적 배열을 사용하면 연속 할당 패턴 덕분에 캐시 프리페칭이 효율적으로 작동하여 접근 시간과 메모리 소비를 줄일 수 있다.^[24]^[25]^[26]

4. 2. 개방 주소법 (Open Addressing)

해싱을 사용하는 탐색 알고리즘은 해시 함수 계산과 충돌 해결 두 부분으로 구성된다. 해시 함수는 탐색 키를 배열 인덱스로 변환하며, 충돌 해결 방법에는 분리 연결법과 개방 주소법이 있다.^[19]

개방 주소법은 충돌 발생 시 테이블 내의 비어있는 다른 번호를 찾는 방식이다. 이때 해시 함수와는 다른 함수를 사용하여 다음 후보 번호를 구하며, 이 함수는 테이블 내 모든 번호를 주사할 수 있도록 선택된다.

4. 2. 1. 개방 주소법의 종류

개방 주소법은 모든 항목 레코드가 버킷 배열 자체에 저장되고 해시 해결이 '''탐사'''를 통해 수행되는 충돌 해결 기술이다. 새 항목을 삽입할 때 해시된 슬롯에서 시작하여 비어 있는 슬롯을 찾을 때까지 "탐사 시퀀스"를 따라 버킷을 검사한다. 항목을 검색할 때는 대상 레코드를 찾거나 사용하지 않는 배열 슬롯을 찾을 때까지 동일한 시퀀스로 버킷을 스캔하며, 이는 검색 실패를 의미한다.^[27]

잘 알려진 탐사 시퀀스는 다음과 같다.

선형 탐사: 탐사 간격이 고정(일반적으로 1)이다.^[28]
이차 탐사: 탐사 간격이 원래 해시 계산에서 제공된 값에 2차 다항식의 연속 출력을 더하여 증가한다.
이중 해싱: 탐사 간격이 보조 해시 함수에 의해 계산된다.

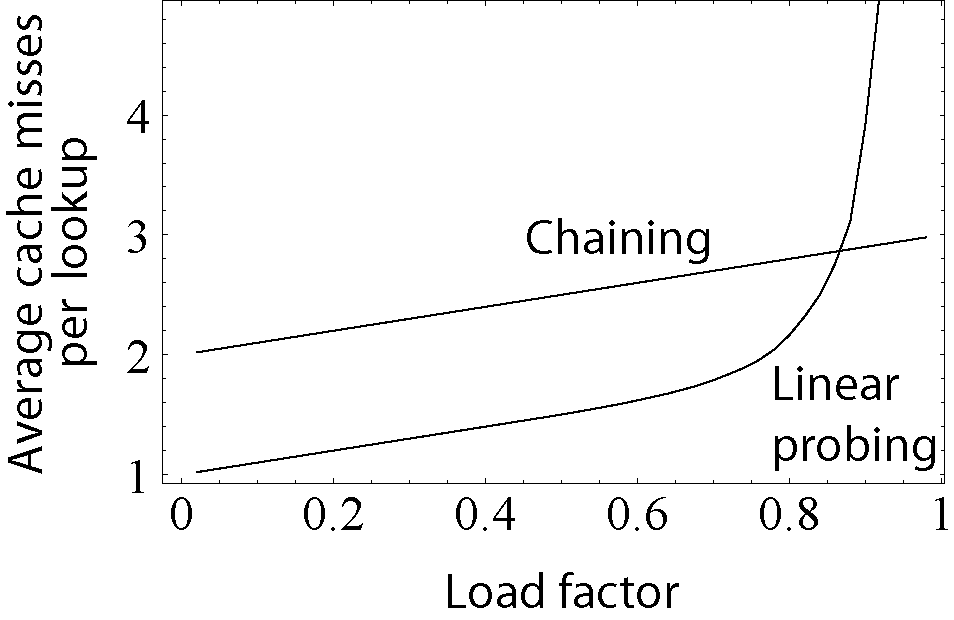
개방 주소법은 로드 팩터

\alpha

가 1에 접근할 때 탐사 시퀀스가 증가하기 때문에 분리 연결(separate chaining)보다 성능이 느릴 수 있다.^[8] 로드 팩터가 1에 도달하면 완전히 채워진 테이블에서 탐사가 무한 루프를 발생시킨다. 선형 탐사의 평균 비용은 해시 함수가 요소들을 테이블 전체에 균등 분포시키는 능력에 따라 달라진다. 이는 클러스터 분석을 피하기 위한 것으로, 클러스터가 형성되면 검색 시간이 증가하기 때문이다.

슬롯이 연속된 위치에 있어 선형 탐사는 CPU 캐시를 더 잘 활용할 수 있으며, 이는 참조 지역성으로 인해 메모리 지연 시간을 줄이는 결과로 이어질 수 있다.^[28]

이 그래프는 체이닝 및 선형 탐사를 사용하여 큰 해시 테이블(캐시 크기를 훨씬 초과)에서 요소를 찾는 데 필요한 평균 CPU 캐시 미스 수를 비교함. 선형 탐사는 더 나은 참조 지역성으로 인해 더 나은 성능을 보이지만 테이블이 가득 차면 성능이 급격히 저하됨.

4. 2. 2. 개방 주소법의 장점

개방 주소법은 모든 항목 레코드가 버킷 배열 자체에 저장되므로 CPU 캐시를 더 잘 활용할 수 있다. 이는 참조 지역성 때문에 메모리 지연 시간을 줄이는 결과로 이어진다.^[28]

4. 2. 3. 개방 주소법의 단점

개방 주소법은 모든 항목 레코드를 버킷 배열 자체에 저장하고 해시 해결을 '''탐사'''를 통해 수행한다. 새 항목을 삽입해야 할 때, 해시된 슬롯에서 시작하여 비어 있는 슬롯을 찾을 때까지 특정 "탐사 시퀀스"를 따라 버킷을 검사한다. 항목을 검색할 때는 대상 레코드를 찾거나 사용하지 않는 배열 슬롯을 찾을 때까지 동일한 시퀀스로 버킷을 스캔하며, 이는 검색 실패를 나타낸다.^[27]

개방 주소법의 성능은 로드 팩터

\alpha

가 1에 접근할 때 탐사 시퀀스가 증가하기 때문에 분리된 체이닝보다 느릴 수 있다.^[8] 로드 팩터가 1에 도달하면, 즉 테이블이 완전히 채워진 경우 탐사가 무한 루프를 발생시킨다. 선형 탐사의 평균 비용은 해시 함수의 요소들을 테이블 전체에 균등 분포시키는 능력에 따라 달라진다. 이는 클러스터 분석을 피하기 위한 것으로, 클러스터가 형성되면 검색 시간이 증가하기 때문이다.

슬롯이 연속된 위치에 있기 때문에 선형 탐사는 CPU 캐시의 더 나은 활용으로 이어질 수 있으며, 이는 참조 지역성으로 인해 메모리 지연 시간을 줄이는 결과를 낳을 수 있다.^[28]

5. 동적 크기 조정

해시 테이블에 항목이 계속 추가되면 부하율(로드 팩터)이 높아진다. 상각된 O(1) 조회 및 삽입 성능을 유지하려면, 해시 테이블의 크기를 동적으로 조정하고 항목들을 새 해시 테이블의 버킷으로 ''재해싱''해야 한다.^[8] 테이블 크기가 바뀌면 나눗셈 연산에 의해 해시 값이 달라지므로, 항목을 그대로 복사할 수 없다.^[37] 항목을 삭제해서 해시 테이블이 "너무 비어"지면, 과도한 메모리 사용량을 줄이기 위해 크기를 조정할 수도 있다.^[38]

일반적으로 원래 해시 테이블 크기의 두 배인 새 해시 테이블을 할당받고, 원래 해시 테이블의 모든 항목의 해시 값을 계산한 다음 새 해시 테이블에 삽입한다. 재해싱은 간단하지만 계산 비용이 많이 든다.^[39]

체이닝 방식에서는 루트 배열이라고 하는 N개 요소의 배열을 준비한다. 루트 배열의 각 요소는 리스트(엔트리 리스트)로, 소수의 엔트리를 저장한다. 엔트리를 저장할 때는 해시 함수를 써서 해시 값을 만든다. 해시 함수는 0부터 N-1까지 정수 값을 생성하며, 균일한 분포와 빠른 계산이 필요하다. 해시 값을 i라고 할 때, 루트 배열의 i번째 엔트리 리스트에 엔트리를 저장한다. 충돌이 발생하면, 엔트리들은 같은 엔트리 리스트에 저장된다.

해시 테이블은 항목 수가 배열 크기에 가까워질수록 충돌이 잦아져 성능이 떨어진다. 이 비율을 ''load factor''(적재율)라고 하며, n/N (n은 항목 수, N은 배열 크기)으로 나타낸다. 체이닝 방식에서는 적재율 증가에 따라 성능이 선형적으로 저하된다.

5. 1. 재해싱 (Rehashing)

해시 테이블에서 항목 수가 증가하면 부하율(로드 팩터)이 높아진다. 조회 및 삽입 연산의 상각된

O(1)

성능을 유지하려면, 해시 테이블의 크기를 동적으로 조정하고 항목들을 새 해시 테이블의 버킷으로 ''재해싱''해야 한다.^[8] 테이블 크기가 바뀌면 나눗셈 연산에 의한 해시 값도 달라지므로, 항목을 그대로 복사할 수는 없다.^[37] 요소를 삭제하여 해시 테이블이 "너무 비어"지면, 과도한 메모리 사용량을 줄이기 위해 크기 조정을 할 수도 있다.^[38]

일반적으로 원래 해시 테이블 크기의 두 배인 새 해시 테이블을 할당받고, 원래 해시 테이블의 모든 항목에 대해 해시 값을 계산한 후 새 해시 테이블에 삽입한다. 재해싱은 간단하지만 계산 비용이 많이 든다.^[39]

해시 테이블은 항목 수가 배열 크기에 가까워질수록 충돌 확률이 높아져 성능이 떨어진다. 이 비율을 ''load factor''(적재율)라고 하며, ''n/N'' (''n''은 항목 수, ''N''은 배열 크기)으로 나타낸다.

체이닝 방식에서는 ''load factor''가 증가하면 성능이 선형적으로 저하된다. 반면 개방 주소법에서는 충돌된 키가 배열의 빈 주소에 저장되므로, ''load factor''가 0.8을 넘으면 성능이 급격히 저하된다.

이 문제를 피하려면 ''load factor''가 일정 값을 초과할 때 더 큰 크기의 해시 테이블을 준비하여 다시 저장하는 '''재해싱''' (rehash)이 필요하다. 이 작업은 모든 요소의 해시 값을 다시 계산하여 새 해시 테이블에 저장하므로 ''O''(n)이지만, 배열 크기를 지수적으로 늘리면 동적 배열의 꼬리 추가 연산처럼 상각 분석을 통해 계산량을 ''O''(1)로 볼 수 있다.

예상되는 항목 수에 대해 미리 충분히 큰 배열을 준비하는 더 간단한 방법도 있지만, 항목 수를 미리 예상할 수 없을 때는 적용하기 어렵다.

5. 1. 1. 재해싱의 대안

분리 연결 해시 테이블은 적재율(데이터 개수 / 버킷 개수)이 증가함에 따라 성능이 점진적으로 저하되며, 크기 조절이 반드시 필요한 시점이 명확하지 않다.^[8] 분리 연결에서 최상의 성능을 보이는 적재율의 최댓값은 일반적으로 1에서 3 사이이다.^[8]

일부 해시 테이블 구현, 특히 실시간 시스템에서는 해시 테이블을 한 번에 확장하는 비용을 감당하기 어려운데, 이는 시간 제약적인 작업을 중단시킬 수 있기 때문이다. 동적 크기 조절을 피할 수 없다면, 점진적으로 크기 조절을 수행하는 것이 해결책이 될 수 있다. 이는 저장 공간의 급격한 증가를 막고, 이전 해시 테이블에서 할당 해제된 큰 메모리 블록으로 인한 메모리 단편화를 방지하여 힙 압축을 유발하는 것을 막는다.^[40] 이러한 경우, 재해싱 작업은 이전 해시 테이블에 할당된 메모리 블록을 확장하여 점진적으로 수행되며, 해시 테이블의 버킷은 변경되지 않는다.

상각 재해싱의 일반적인 방법은 두 개의 해시 함수

h_\text{old}

와

h_\text{new}

를 유지하는 것이다. 새로운 해시 함수에 따라 버킷 항목을 재해싱하는 과정을 ''정리''라고 하며, 이는

\mathrm{Add}(\mathrm{key})

,

\mathrm{Get}(\mathrm{key})

및

\mathrm{Delete}(\mathrm{key})

와 같은 연산을

\mathrm{Lookup}(\mathrm{key}, \text{command})

래퍼를 통해 캡슐화하여 명령 패턴을 통해 구현된다. 버킷의 각 요소가 재해싱되는 절차는 다음과 같다.

$\mathrm{Table}[h_\text{old}(\mathrm{key})]$ 버킷을 정리한다.
$\mathrm{Table}[h_\text{new}(\mathrm{key})]$ 버킷을 정리한다.
''명령''이 실행된다.

선형 해싱은 한 번에 한 버킷씩 테이블을 동적으로 늘리거나 줄일 수 있는 해시 테이블 구현 방식이다.^[41]

6. 성능

분리 연결 해시 테이블은 로드 팩터가 증가함에 따라 성능이 점진적으로 저하되며, 크기 조절이 절대적으로 필요한 고정 지점은 없다.^[8] 분리 연결에서 최상의 성능을 제공하는 $\alpha_{\max}$ 값은 일반적으로 1과 3 사이이다.^[8]

해시 값의 균등 분포는 해시 함수의 기본적인 요구 사항이다. 균등하지 않은 분포는 충돌 횟수를 증가시키고 이를 해결하는 비용을 증가시킨다. 균등성은 설계를 통해 보장하기 어려울 때도 있지만, 통계적 검정을 사용하여 경험적으로 평가할 수 있다. 예를 들어 이산 균등 분포에 대한 피어슨 카이 제곱 검정이 있다.^[14]^[15]

분포는 응용 프로그램에서 발생하는 테이블 크기에 대해서만 균등해야 한다. 특히 테이블 크기를 정확하게 두 배로 늘리거나 줄이는 동적 크기 조정을 사용하는 경우, 해시 함수는 크기가 2의 거듭제곱일 때만 균등해야 한다. 여기서 인덱스는 해시 함수의 비트 범위로 계산할 수 있다. 반면에 일부 해싱 알고리즘은 크기가 소수인 것을 선호한다.^[16]

오픈 어드레싱 방식의 경우, 해시 함수는 두 개 이상의 키를 연속적인 슬롯에 매핑하는 클러스터링도 피해야 한다. 이러한 클러스터링은 적재율이 낮고 충돌이 드물더라도 조회 비용을 급증시킬 수 있다. 널리 사용되는 곱셈 해시는 특히 클러스터링 동작이 좋지 않다고 알려져 있다.^[16]^[4]

K-독립 해싱은 주어진 유형의 해시 테이블에 대해 특정 해시 함수가 나쁜 키 집합을 갖지 않음을 증명하는 방법을 제공한다. 선형 탐사 및 뻐꾸기 해싱과 같은 충돌 해결 방식에 대해 여러 K-독립성 결과가 알려져 있다. K-독립성은 해시 함수가 작동함을 증명할 수 있으므로, 가능한 가장 빠른 해시 함수를 찾는 데 집중할 수 있다.^[17]

해시 테이블의 성능은 해시 함수가 해시 테이블의 항목에 대해 준 무작위 숫자( $\sigma$ )를 생성하는 능력에 달려 있다. 여기서 $K$ , $n$ , $h(x)$ 는 각각 키, 버킷 수 및 해시 함수를 나타내며 $\sigma\ =\ h(K)\ \%\ n$ 이다. 해시 함수가 서로 다른 키( $K_1 \ne K_2,\ h(K_1)\ =\ h(K_2)$ )에 대해 동일한 $\sigma$ 를 생성하면, 이는 ''충돌''을 발생시키며, 이는 다양한 방식으로 처리된다. 해시 테이블에서 연산의 상수 시간 복잡성( $O(1)$ )은 해시 함수가 충돌하는 인덱스를 생성하지 않는다는 조건 하에 전제되며, 따라서 해시 테이블의 성능은 선택된 해시 함수가 인덱스를 분산시키는 능력에 정비례한다.^[42]

7. 응용

해시 테이블은 다양한 종류의 메모리 내 테이블을 구현하는 데 일반적으로 사용되며, 연관 배열을 구현하는 데에도 사용된다.^[43] 디스크 드라이브 기반 데이터 구조 및 데이터베이스 인덱스 (예: dbm)에도 사용될 수 있지만, 이러한 응용 분야에서는 B-트리가 더 널리 사용된다.^[44]

또한, 해시 테이블은 느린 매체에 주로 저장된 데이터에 대한 접근 속도를 높이는 데 사용되는 보조 데이터 테이블인 캐시를 구현하는 데 사용될 수 있다. 이 응용 프로그램에서 해시 충돌은 충돌하는 두 항목 중 하나를 버리는 방식으로 처리할 수 있다. 일반적으로 테이블에 현재 저장된 이전 항목을 지우고 새 항목으로 덮어쓰므로 테이블의 모든 항목은 고유한 해시 값을 갖는다.^[45]^[46]

해시 테이블은 특정 순서 없이 고유한 값을 저장할 수 있는 집합 (자료 구조)의 구현에도 사용될 수 있다. 집합은 요소 검색보다는 컬렉션 내 값의 멤버십을 테스트하는 데 일반적으로 사용된다.^[47] 전치표는 탐색된 각 섹션에 대한 정보를 저장하는 복잡한 해시 테이블이다.^[48]

8. 프로그래밍 언어별 구현

많은 프로그래밍 언어가 해시 테이블 기능을 제공하며, 이는 내장된 연관 배열 또는 표준 라이브러리 모듈 형태로 제공된다.^[49]

언어	자료 구조
자바스크립트	객체^[49], `Map` ^[50]
C++11	`unordered_map`^[51]
Go	내장 `map`^[52]
자바	`HashSet`, `HashMap`, `LinkedHashSet`, `LinkedHashMap` 제네릭 컬렉션^[53]
파이썬	내장 `dict`^[54]
루비	내장 `Hash` (루비 2.4부터 개방 주소 지정 모델 사용)^[55]
러스트	`HashMap`, `HashSet`^[56]
.NET	`HashSet`, `Dictionary`^[57]^[58] ( C#, VB.NET 등에서 사용 가능)^[59]
AWK	연관 배열
Perl	Hash
C++	STL의 `std::unordered_map`
Common Lisp	`hash-table` 클래스
Nim	`std/tables`

자바스크립트에서 "객체"는 키-값 쌍("속성"이라고 함)의 변경 가능한 컬렉션이며, 각 키는 문자열 또는 보장된 고유 "기호"이다. 키로 사용될 때 다른 모든 값은 먼저 문자열로 강제 변환된다. 7가지 "기본" 데이터 유형 외에 자바스크립트의 모든 값은 객체이다.^[49] ECMAScript 2015는 임의의 값을 키로 허용하는 `Map` 데이터 구조도 추가했다.^[50]

참조

_[1] 서적 Introduction to Algorithms Massachusetts Institute of Technology
_[2] 서적 Algorithms and Data Structures Springer 2008
_[3] 웹사이트 Lecture 13: Amortized Algorithms, Table Doubling, Potential Method http://videolectures[...] 2005-09-01
_[4] 서적 The Art of Computer Programming Addison-Wesley
_[5] 서적 Introduction to Algorithms MIT Press and McGraw-Hill
_[6] 서적 Hashing in Computer Science 2010
_[7] 서적 Handbook of Data Structures and Applications 2004
_[8] 웹사이트 CS 312: Hash tables and amortized analysis https://www.cs.corne[...] Cornell University, Department of Computer Science 2008-10-26
_[9] 웹사이트 CS140 Lecture notes -- Hashing http://web.eecs.utk.[...]
_[10] 학술지 Hash Table Methods 1975-03-01
_[11] 학회 Perfect Hashing for Network Applications
_[12] 학회 Hash, displace, and compress http://cmph.sourcefo[...] Springer
_[13] 학술지 Empirical studies of some hashing functions 2003-02-01
_[14] 학술지 On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling https://zenodo.org/r[...]
_[15] 학술지 Karl Pearson and the Chi-Squared Test
_[16] 웹사이트 Prime Double Hash Table https://www.concentr[...] 1997-03-01
_[17] 학술지 New hash functions and their use in authentication and set equality 1981-06-01
_[18] 서적 The Art of Computer Programming: Volume 3: Sorting and Searching https://dl.acm.org/d[...] Addison-Wesley Professional 1998-04-24
_[19] 서적 Algorithms https://algs4.cs.pri[...] Addison-Wesley Professional
_[20] 서적 Introduction to Algorithms Massachusetts Institute of Technology
_[21] 웹사이트 Lecture 2 http://courses.csail[...] 2003-03-01
_[22] 학술지 Examining computational geometry, van Emde Boas trees, and hashing from the perspective of the fusion tree
_[23] 서적 String Processing and Information Retrieval 2005
_[24] 학술지 Engineering scalable, cache and space efficient tries for strings 2010-10-01
_[25] 학회 Cache-conscious Collision Resolution in String Hash Tables 2005-10-01
_[26] 학회 Fast and Compact Hash Tables for Integer Keys http://crpit.com/con[...]
_[27] 서적 Data Structures Using C Prentice Hall
_[28] 서적 Algorithms — ESA 2001
_[29] 서적 The design and analysis of coalesced hashing https://archive.org/[...] Oxford University Press
_[30] 서적 Algorithms — ESA 2001
_[31] 서적 Distributed Computing 2008
_[32] 서적 Robin Hood Hashing https://cs.uwaterloo[...] University of Waterloo, Dept. of Computer Science
_[33] 학술지 Analysis of Robin Hood and Other Hashing Algorithms Under the Random Probing Model, With and Without Deletions 2019-07-01
_[34] 웹사이트 Lecture 13: Hash tables https://www.cs.corne[...] Cornell University, Department of Computer Science
_[35] 웹사이트 JavaHyperText and Data Structure: Robin Hood Hashing https://www.cs.corne[...] Cornell University, Department of Computer Science
_[36] 기술보고서 External Robin Hood Hashing https://legacy.cs.in[...] 2021-11-02
_[37] 웹사이트 Chapter C5: Hash Tables https://people.compu[...] Clemson University 2023-12-04
_[38] 웹사이트 Intro to Algorithms: Resizing Hash Tables https://courses.csai[...] Massachusetts Institute of Technology, Department of Computer Science 2021-11-09
_[39] 서적 Data Structures Using C Oxford University Press 2014
_[40] 학술지 Hash Tables for Embedded and Real-time systems https://users.cs.nor[...] Washington University in St. Louis 2021-11-09
_[41] 학회 Linear hashing: A new tool for file and table addressing https://www.cs.cmu.e[...] Carnegie Mellon University 2021-11-10
_[42] 웹사이트 Analysing and Improving Hash Table Performance https://www.tvandijk[...] University of Twente 2021-12-31
_[43] 서적 Introduction to Algorithms MIT Press and McGraw-Hill
_[44] 웹사이트 Indexes and external sorting https://edux.pjwstk.[...] Polsko-Japońska Akademia Technik Komputerowych 2022-03-26
_[45] 학술지 Cache hit ratio maximization in device-to-device communications overlaying cellular networks 2020-02
_[46] 웹사이트 Understanding Caching https://www.linuxjou[...] Linux Journal 2004-01-01
_[47] 웹사이트 Set & Hash Tables https://userweb.cs.t[...] Texas State University 2014
_[48] 웹사이트 Transposition Table - Chessprogramming wiki https://www.chesspro[...] 2020-05-01
_[49] 웹사이트 JavaScript data types and data structures - JavaScript MDN https://developer.mo[...] 2022-07-24
_[50] 웹사이트 Map - JavaScript MDN https://developer.mo[...] 2023-07-15
_[51] 웹사이트 Programming language C++ - Technical Specification http://www.open-std.[...] International Organization for Standardization 2022-02-08
_[52] 웹사이트 The Go Programming Language Specification https://go.dev/ref/s[...] 2023-01-01
_[53] 웹사이트 Lesson: Implementations (The Java™ Tutorials > Collections) https://docs.oracle.[...] 2018-04-27
_[54] 학술지 Redis rehash optimization based on machine learning
_[55] 웹사이트 Ruby 2.4 Released: Faster Hashes, Unified Integers and Better Rounding https://blog.heroku.[...] 2019-07-03
_[56] 웹사이트 doc.rust-lang.org https://doc.rust-lan[...] 2022-12-14
_[57] 웹사이트 HashSet Class (System.Collections.Generic) https://learn.micros[...] 2023-07-01
_[58] 웹사이트 Dictionary Class (System.Collections.Generic) https://learn.micros[...] 2024-01-16
_[59] 웹사이트 VB.NET HashSet Example https://www.dotnetpe[...]
_[60] 서적 Handbook of Datastructures and Applications https://archive.org/[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com