호너의 방법
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
호너의 방법은 다항식의 값을 효율적으로 계산하는 알고리즘으로, 특히 다항식의 나눗셈과 근을 찾는 데 유용하게 사용된다. 이 방법은 다항식을 곱셈 횟수를 줄여 계산 속도를 향상시키며, 19세기 초 윌리엄 조지 호너에 의해 널리 알려졌지만, 그 이전에도 유사한 방법이 중국, 페르시아 등에서 사용되었다. 호너의 방법은 다항식 계산, 이진 곱셈 및 나눗셈, 다른 기수법 간의 변환 등 다양한 분야에 응용된다.
더 읽어볼만한 페이지
- 대수학 - 다항식
다항식은 변수, 계수, 상수항으로 구성되어 덧셈, 뺄셈, 곱셈, 거듭제곱 연산으로 결합된 항들의 유한한 합으로 표현되는 식이며, 대수 방정식 해를 구하는 데 중요하고 현대 수학에서 폭넓게 활용된다. - 대수학 - 상수
상수는 변하지 않는 일정한 값을 가지는 수로, 함수에서 변수와 대비되며 수식 내에서 고정된 값을 갖고, 원주율, 자연로그의 밑, 허수 i 등이 대표적인 예시이다. - 다항식 - 르장드르 다항식
르장드르 다항식은 르장드르 미분 방정식의 해로 정의되는 직교 다항식 계열로, 생성 함수, 로드리게스 공식, 또는 점화식을 통해 정의될 수 있으며, 물리학, 공학, 수치해석 등 다양한 분야에서 응용된다. - 다항식 - 행렬식
행렬식은 정사각 행렬에 대해 정의되는 값으로, 선형 방정식의 해를 구하고 선형 독립성을 확인하며 기저의 방향과 부피를 계산하는 데 사용되며, 가우스 소거법 등의 계산 기법과 가역성 판단, 고유값 연관성 등의 성질을 갖는다. - 수치해석학 - 수학적 최적화
수학적 최적화는 주어진 집합에서 실수 또는 정수 변수를 갖는 함수의 최댓값이나 최솟값을 찾는 문제로, 변수 종류, 제약 조건, 목적 함수 개수에 따라 다양한 분야로 나뉘며 여러 학문 분야에서 활용된다. - 수치해석학 - 선형대수학
선형대수학은 벡터, 벡터 공간, 행렬 등의 개념으로 선형 방정식과 선형 변환을 연구하는 수학 분야로, 선형성을 활용해 행렬로 표현 및 계산하며, 연립일차방정식 해법, 고유값/고유벡터를 통한 행렬 분석, 벡터 공간의 기저와 차원 등을 다루고 물리학, 공학, 컴퓨터 과학 등 다양한 분야에 응용된다.
| 호너의 방법 | |
|---|---|
| 개요 | |
| 이름 | 호너법 호너의 방법 |
| 영어 이름 | Horner's method |
| 분야 | 수학, 컴퓨터 과학 |
| 종류 | 다항식 계산 알고리즘 |
| 상세 정보 | |
| 발명가 | 윌리엄 조지 호너 |
| 발명 시기 | 1819년 |
| 용도 | 다항식 계산 다항식 나눗셈 기수 변환 |
| 관련 항목 | 조립제법 클렌쇼 알고리즘 데카르트 부호 규칙 |
| 알고리즘 | |
| 입력 | 다항식 계수 (a₀, a₁, ..., aₙ) 계산할 값 (x) |
| 출력 | 다항식 값 (a₀ + a₁x + ... + aₙxⁿ) |
| 단계 | 2. i를 n-1부터 0까지 감소시키면서 다음을 반복: result = result * x + aᵢ |
| 복잡도 | 시간 복잡도: O(n) 공간 복잡도: O(1) |
| 활용 | |
| 다항식 계산 | 주어진 x 값에서 다항식의 값을 효율적으로 계산 |
| 다항식 나눗셈 | 다항식을 (x - r)로 나눌 때 몫과 나머지를 계산 |
| 기수 변환 | 숫자를 한 기수에서 다른 기수로 변환 |
| 장점 | |
| 효율성 | 직접 계산하는 것보다 곱셈과 덧셈 연산 횟수를 줄여 더 효율적 |
| 안정성 | 부동소수점 연산에서 오류 누적을 줄임 |
| 역사적 맥락 | |
| 기원 | 윌리엄 조지 호너가 1819년에 발표했지만, 이미 파올로 루피니가 이전에 발견 |
| 다른 이름 | 호너-루피니 방법이라고도 불림 |
| 참고 자료 | |
| 관련 서적 | 컴퓨터 알고리즘 (Cormen, Leiserson, Rivest, Stein) |
| 외부 링크 | |
| 매스월드 | 호너의 규칙 - 매스월드 |
2. 다항식 계산
주어진 다항식 (여기서 은 상수 계수)의 값을 의 특정 값 에서 계산하는 방법을 설명한다.
이를 위해 새로운 상수 수열을 다음과 같이 재귀적으로 정의한다.
:
그러면 는 의 값이다.
이는 다항식을 다음과 같은 형태로 표현할 수 있기 때문이다.
:
위 식에 를 반복적으로 대입하면 임을 알 수 있다.
계수 로 구성된 일변수 x의 n차 다항식 의 에서의 값 를 구할 때, 각 항을 직접 계산하여 더하는 방법은 n(n+1)/2 회의 곱셈이 필요하다.
하지만, 다항식 p(x)를 으로 변형하면 곱셈 횟수를 n회로 줄일 수 있다. 이처럼 다항식을 변형하여 적은 연산 횟수로 다항식의 값을 구하는 방법을 '''호너의 방법''' (Horner's rule)이라고 한다.
2. 1. 계산 예시
다음은 호너의 방법을 사용하여 다항식의 값을 계산하는 예시이다.'''예시 1:''' 을 에서 평가
조립제법을 사용하면 다음과 같다.
| x0 | x3 | x2 | x1 | x0 |
|---|---|---|---|---|
| 3 | 2 | −6 | 2 | −1 |
| 6 | 0 | 6 | ||
| 2 | 0 | 2 | 5 |
- 세 번째 행의 각 항목은 처음 두 행의 항목을 더한 값이다.
- 두 번째 행의 각 항목은 x값 (이 경우 3)과 바로 왼쪽에 있는 세 번째 행 항목을 곱한 값이다.
- 첫 번째 행의 항목은 평가할 다항식의 계수이다.
다항식 나머지 정리에 의해, 나머지는 와 같으므로, 이다.
이 예제에서 이므로, 세 번째 행의 항목은 순서대로 가 된다.
'''예시 2:''' 을 로 나누는 경우
| 1 | −6 | 11 | −6 | |
|---|---|---|---|---|
| 2 | 2 | −8 | 6 | |
| 1 | −4 | 3 | 0 |
몫은 이고, 나머지는 0이다.
'''예시 3:''' 를 로 나누는 경우
| 4 | −6 | 0 | 3 | −5 | |
|---|---|---|---|---|---|
| 0.5 | 2 | −2 | −1 | 1 | |
| 2 | −2 | −1 | 1 | −4 |
호너의 방법(조립제법)은 다항식 를 형태의 일차식으로 나눌 때 몫과 나머지를 구하는 방법이다. 한국에서는 조립제법이라는 이름으로 고등학교 수학 교육과정에서 다항식 나눗셈을 가르칠 때 사용된다.[1]
세 번째 행은 처음 두 행의 합을 2로 나눈 값이다. 두 번째 행의 각 항목은 1과 왼쪽에 있는 세 번째 행 항목을 곱한 값이다. 따라서,
이다.
3. 다항식 나눗셈 (조립제법)
주어진 다항식은 다음과 같다.
여기서 계수 은 상수이다. 의 특정 값 에서 다항식의 값을 계산하기 위해 다음과 같은 새로운 상수 수열을 재귀적으로 정의한다.
그러면 는 의 값이 된다. 이를 통해 다음 식을 얻을 수 있다.
이 식은 의 결과를 빠르게 제공하며, (즉, )은 나눗셈의 나머지이다. 만약 가 의 근이면 (나머지가 0)이 되고, 는 로 인수분해될 수 있다.[1]
연속적인 값을 찾기 위해, (과 같음)을 먼저 결정하고, 다음 공식을 사용하여 에 도달할 때까지 재귀적으로 계산한다.
3. 1. 나눗셈 예시
다음은 조립제법을 이용한 다항식 나눗셈의 예시이다.
'''예시 1'''
을 으로 나누는 경우:
| x0 | x3 | x2 | x1 | x0 |
|---|---|---|---|---|
| 3 | 2 | −6 | 2 | −1 |
| 6 | 0 | 6 | ||
| 2 | 0 | 2 | 5 |
세 번째 행은 첫 번째 행과 두 번째 행의 합으로 구해진다. 두 번째 행의 각 항은 ''x'' 값 (이 예시에서는 3)과 바로 왼쪽에 있는 세 번째 행의 값을 곱하여 얻어진다. 첫 번째 행은 나누어지는 다항식 의 계수이다. 따라서 를 으로 나눈 나머지는 5이다.
다항식 나머지 정리에 의해 나머지는 이므로, 임을 알 수 있다.
세 번째 행의 값들은 몫인 2차 다항식()의 계수들이고, 나머지는 5이다.
'''예시 2'''
을 로 나누는 경우:
| 1 | −6 | 11 | −6 | |
|---|---|---|---|---|
| 2 | 2 | −8 | 6 | |
| 1 | −4 | 3 | 0 |
몫은 이다.
'''예시 3'''
를 로 나누는 경우:
| 4 | −6 | 0 | 3 | −5 | |
|---|---|---|---|---|---|
| 0.5 | 2 | −2 | −1 | 1 | |
| 2 | −2 | −1 | 1 | −4 |
세 번째 행은 첫 번째 행과 두 번째 행의 합을 2로 나눈 값이다. 두 번째 행의 각 항은 1과 왼쪽에 있는 세 번째 행의 값을 곱하여 얻어진다. 따라서,
'''예시 4'''
을
로 나누는 경우: 몫은
이고, 나머지는
이다.
| 1 | - 5 | + 9 | - 6 | - 16 | + 13 | |
|---|---|---|---|---|---|---|
| + 3 | + 3 | - 6 | ||||
| - 2 | - 2 | + 4 | ||||
| + 3 | - 2 | |||||
| + 1 | - 2 | |||||
| 1 | - 2 | + 1 | + 1 | - 15 | + 11 |
4. 효율성
호너의 방법은 주어진 다항식을 효율적으로 계산하는 방법이다. 일반적인 다항식은 다음과 같이 표현된다.
:
여기서 은 상수 계수이다. 이 다항식을 의 특정 값 에서 계산하려면, 호너의 방법을 사용하면 효율적이다.
호너의 방법은 다음과 같이 다항식을 변형하여 계산한다.
:
이렇게 하면 곱셈 횟수를 줄일 수 있다. 예를 들어, 모노미얼 형태의 차 다항식을 계산하려면 최대 번의 덧셈과 번의 곱셈이 필요하다. 하지만 호너의 방법을 사용하면 번의 덧셈과 번의 곱셈만으로 계산할 수 있다.[3]
이는 알렉산더 오스트로프스키가 1954년에 필요한 덧셈 횟수가 최소임을 증명했고,[4] 빅터 판이 1966년에 곱셈 횟수가 최소임을 증명했다.[5]
컴퓨터 연산에서 호너의 방법은 단순 계산보다 더 빠르고, 메모리 사용량도 적다. 특히, 부동 소수점 연산에서 호너의 방법은 단순 계산보다 더 빠르다.
4. 1. 병렬 계산
호너의 방법은 모든 연산이 순차적으로 종속되어 있어, 최신 컴퓨터의 명령어 수준 병렬 처리 기능을 충분히 활용하기 어렵다는 단점이 있다. 그러나 매우 높은 차수의 다항식을 계산해야 하는 경우, 다항식을 여러 부분으로 나누어 병렬 처리를 할 수 있다.예를 들어, 다항식 는 다음과 같이 두 부분으로 나눌 수 있다.
:
이때, 와 는 각각 호너의 방법을 사용하여 병렬로 계산할 수 있다.
더 일반적으로, 다항식을 ''k''개의 부분으로 나누어 계산할 수 있다.
:
여기서 내부 합산은 호너의 방법을 사용하여 별도로 병렬 계산할 수 있다. 이 방법은 기본적인 호너의 방법보다 약간 더 많은 연산이 필요하지만, 대부분의 연산에 대해 ''k'' 방식의 SIMD 실행을 허용하여 계산 속도를 높일 수 있다. 최신 컴파일러는 이러한 방식으로 다항식을 평가하기도 하지만, 부동 소수점 계산의 경우에는 재결합 수학을 활성화해야 한다.
5. 부동소수점 곱셈과 나눗셈에의 응용
호너의 방법은 마이크로컨트롤러와 같이 하드웨어 곱셈기가 없는 환경에서 이진수 곱셈과 나눗셈을 수행하는 데 유용하다. 곱할 이진수 중 하나를 이고 인 간단한 다항식으로 표현하여 계산을 단순화한다. 이진법에서 이므로, 2의 거듭제곱을 반복적으로 인수분해하여 곱셈을 수행한다.
이진수 곱셈은 산술 시프트 연산, 덧셈 및 뺄셈만으로 빠르게 계산될 수 있다. 이진법에서 2의 거듭제곱을 곱하는 것은 레지스터 시프트 연산으로 간단히 처리된다. 예를 들어, 2를 곱하는 것은 왼쪽 산술 시프트, 2-1을 곱하는 것은 오른쪽 산술 시프트로 계산된다.[7]
5. 1. 응용 예시
호너의 방법은 마이크로컨트롤러에서 하드웨어 곱셈기 없이 이진수 곱셈과 나눗셈을 빠르게 수행하는 효율적인 방법이다. 곱할 이진수 중 하나를 이고, 인 다항식으로 표현한 후, ''x'' (또는 ''x''의 거듭제곱)를 반복적으로 인수분해한다. 이진법에서 이므로, 2의 거듭제곱이 반복적으로 인수분해된다.예를 들어, 0.15625와 ''m''을 곱하는 경우 다음과 같이 계산할 수 있다.
두 이진수 ''d''와 ''m''의 곱은 다음 단계를 통해 계산한다.
# 중간 결과를 저장하는 레지스터를 ''d''로 초기화한다.
# ''m''의 최하위(가장 오른쪽) 비트부터 시작하여, 0이 아닌 비트를 찾는다.
#* 다음으로 유의미한 0이 아닌 비트까지 비트 위치의 개수를 센다. 더 유의미한 비트가 없다면 현재 비트 위치의 값을 사용한다.
#* 해당 값을 사용하여 중간 결과를 저장하는 레지스터에서 왼쪽 시프트 연산을 해당 비트 수만큼 수행한다.
# 0이 아닌 모든 비트를 세었다면, 중간 결과 레지스터는 이제 최종 결과를 담고 있다. 그렇지 않으면 d를 중간 결과에 더하고, ''m''의 다음으로 유의미한 비트로 2단계부터 다시 시작한다.
일반적으로 비트 값()을 갖는 이진수에 대해, 곱은 다음과 같이 표현할 수 있다.
0 값을 갖는 계수를 가진 항을 제거하면, 다음 식을 얻을 수 있다.
분모는 모두 1과 같으므로, 식은 다음과 같이 축소된다.
또는
이진수에서 2의 거듭제곱을 곱하는 것은 레지스터 시프트 연산으로 계산할 수 있다. 즉, 2를 곱하는 것은 왼쪽 산술 시프트이고, 2-1을 곱하는 것은 오른쪽 산술 시프트이다.
따라서 곱셈 결과는 산술 시프트 연산, 덧셈 및 뺄셈만으로 빠르게 계산할 수 있다. 이 방법은 단일 명령 시프트-앤드-어큐뮬레이트를 지원하는 프로세서에서 특히 빠르다.[7]
6. 기타 응용
호너의 방법은 다른 위치적 기수법 간의 변환에도 사용될 수 있다. 이때 'x'는 수 체계의 밑수가 되며, 'a''i' 계수는 주어진 숫자의 밑수 'x' 표현의 자릿수가 된다.[8] 또한 'x'가 행렬인 경우에도 호너의 방법을 사용할 수 있으며, 이 경우 계산 효율성이 더욱 커진다. 그러나 이러한 경우에는 더 빠른 방법이 알려져 있다.[8]
7. 다항식의 근 찾기
뉴턴 방법과 긴 나눗셈 알고리즘을 결합하여 다항식의 실근을 근사할 수 있다. 주어진 다항식에서 가장 큰 영점부터 차례대로 찾아 나가는 방식이다. 이 방법은 다음 두 단계로 이루어진다.[9]
1. 뉴턴 방법을 사용하여 주어진 다항식의 가장 큰 영점을 찾는다.
2. 호너의 방법을 사용하여 찾은 영점으로 다항식을 나누어 차수를 낮춘다.
위의 두 단계를 모든 실근을 찾을 때까지 반복한다. 만약 근사값이 충분히 정확하지 않다면, 그 값을 초기 추측값으로 사용하여 뉴턴 방법을 다시 적용할 수 있다.[9]
7. 1. 근 찾기 예시
다항식
:p|6영어(x) = (x+8)(x+5)(x+3)(x-2)(x-3)(x-7)
를 생각해 보자. 이 다항식은 다음과 같이 전개될 수 있다.
:p|6영어(x) = x6 + 4x5 - 72x4 -214x3 + 1127x2 + 1602x -5040.
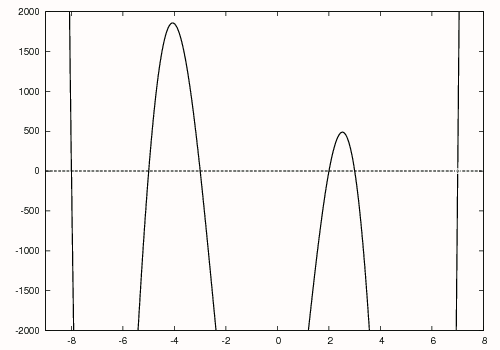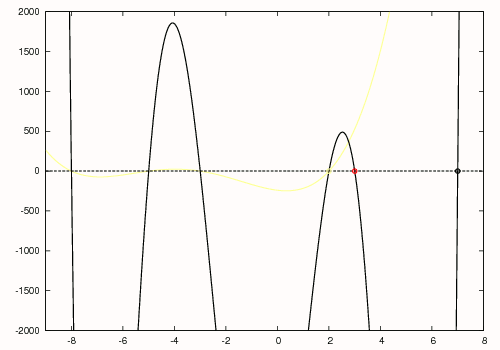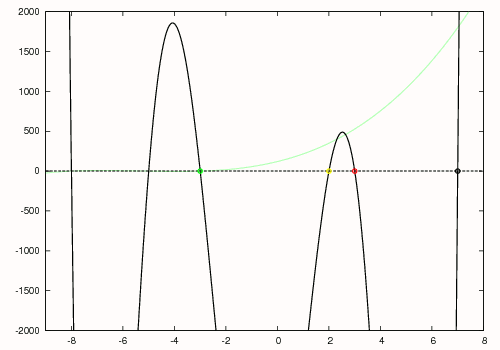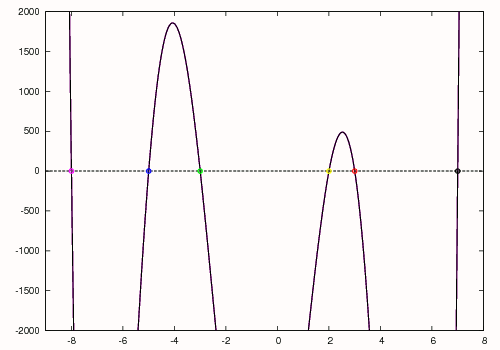
이 다항식의 가장 큰 근이 7임을 알고 있으므로 초기 추측값을 8로 설정할 수 있다. 뉴턴 방법을 사용하면 그림의 오른쪽에 검은색으로 표시된 것처럼 7이라는 첫 번째 근을 찾을 수 있다. 다음으로 p|6영어(x)를 (x-7)로 나누어
:p|5영어(x) = x5 + 11x4 + 5x3 - 179x2 - 126x + 720
을 얻는데, 이것은 그림 오른쪽에 빨간색으로 그려져 있다. 뉴턴 방법을 사용하여 이 다항식의 가장 큰 근을 찾으며, 초기 추측값은 7이다. 이 다항식의 가장 큰 근은 원래 다항식의 두 번째로 큰 근에 해당하며, 3에서 발견되고 빨간색으로 묶여 있다. 이제 5차 다항식을 (x-3)으로 나누어
:p|4영어(x) = x4 + 14x3 + 47x2 - 38x - 240
을 얻는데, 이것은 노란색으로 표시되어 있다. 이 다항식의 근은 다시 뉴턴 방법을 사용하여 2에서 발견되고 노란색으로 묶여 있다. 이제 호너의 방법을 사용하여
:p|3영어(x) = x3 + 16x2 + 79x + 120
을 얻는데, 이것은 녹색으로 표시되어 있으며 -3에서 근을 갖는 것으로 발견되었다. 이 다항식은 더 줄여져
:p|2영어(x) = x2 + 13x + 40
이 되는데, 이것은 파란색으로 표시되어 있으며 -5의 근을 얻는다. 원래 다항식의 마지막 근은 마지막 근을 뉴턴 방법의 초기 추측값으로 사용하거나, p|2영어(x)를 줄이고 선형 방정식을 풀어 찾을 수 있다. 예상되는 근 -8, -5, -3, 2, 3 및 7이 발견되었다.
8. 다항식의 나눗셈 차분
다음과 같은 다항식이 주어졌을 때,
호너의 방법을 수정하여 나눗셈 차분 를 계산할 수 있다.[10] 이 때, 다음과 같이 진행한다.
계산이 완료되면 다음을 얻는다.
이 나눗셈 차분 계산은 와 를 개별적으로 평가하는 것보다 반올림 오류가 적으며, 특히 일 때 그렇다. 이 방법에서 를 대입하면 , 즉 의 도함수를 얻는다.
9. 역사
결과: ''x''=840[11]||right||200px]]
"연속 근사를 통한 모든 차수의 수치 방정식 풀이의 새로운 방법"이라는 제목의 호너의 논문[12]은 1819년 7월 1일 런던 왕립 학회 회의에서 발표되었으며, 1823년에 후속 논문이 발표되었다.[12] 1819년 호너의 논문은 1820년 4월호 ''The Monthly Review: or, Literary Journal''에서 따뜻하고 폭넓게 환영받았지만, 찰스 배비지의 기술 논문은 무시되었다. 1821년 9월 ''The Monthly Review''의 리뷰는 홀드레드가 수치 방정식의 직접적이고 일반적인 실용적 해법을 최초로 발견한 사람이라고 결론지었다. 풀러[13]는 호너의 1819년 논문이 이후 "호너의 방법"으로 알려진 것과 다르며, 이 방법의 우선순위는 홀드레드(1820)에게 주어져야 한다고 밝혔다.
영국 동시대 사람들과 달리, 호너는 아르보가스트의 연구를 비롯한 유럽 대륙의 문헌에 의존했다. 호너는 존 보네캐슬의 대수학 책을 자세히 읽었지만, 파올로 루피니의 연구는 무시했다.
호너가 이 방법을 접근 가능하고 실용적으로 만드는 데 기여했지만, 호너 이전에도 오랫동안 알려져 있었다. 다음은 호너의 방법이 알려진 순서를 역순으로 나열한 것이다.
- 파올로 루피니 (1809년, 루피니 규칙 참조)[14][15]
- 아이작 뉴턴 (1669년)[16][17]
- 14세기 중국 수학자 주세걸[15]
- 13세기 중국 수학자 친 지우샤오 (''수학 구장''에 등장)
- 12세기 페르시아 수학자 샤라프 알딘 알 투시 (삼차 방정식의 일반적인 경우에 이 방법을 처음 사용)[18]
- 11세기 (송나라) 중국 수학자 자 셴
- 유 휘 (3세기)가 편집한 한나라 (기원전 202년~서기 220년)의 중국 작품 ''구장산술''[19]
친 지우샤오는 ''수서구장''(''수학 구장''; 1247)에서 11세기 송나라 수학자 자 셴의 초기 연구에 기반한 다항 방정식 풀이를 위한 호너형 방법들을 제시했다. 요시오 미카미는 ''중국과 일본의 수학 발전'' (1913)에서 "호너의 훌륭한 과정이 유럽보다 적어도 거의 6세기 전에 중국에서 사용되었다는 사실을 누가 부인할 수 있겠는가"라고 썼다.[20]
울리히 리브레히트는 "이 절차는 중국의 발명품이다. 이 방법은 인도에서는 알려지지 않았다."라고 결론지었다. 그는 피보나치가 아랍인들로부터 그것을 배웠고, 아랍인들은 아마도 중국인들에게서 빌려왔을 것이라고 말했다.[21] 제곱근과 세제곱근의 추출은 유 휘가 ''구장산술''의 문제 IV.16 및 22와 관련하여 논의했으며, 7세기 왕 샤오퉁은 계고산경에 기술된 근사법으로 독자들이 삼차 방정식을 풀 수 있다고 가정한다.
참조
[1]
문서
600 years earlier, by the Chinese mathematician [[Qin Jiushao]] and 700 years earlier, by the Persian mathematician [[Sharaf al-Dīn al-Ṭūsī]]
[2]
harvnb
Pan
[3]
harvnb
Pankiewicz
[4]
harvnb
Ostrowski
[5]
harvnb
Pan
[6]
harvnb
Knuth
[7]
harvnb
Kripasagar
[8]
harvnb
Higham
[9]
harvnb
Kress
[10]
harvnb
Fateman
[11]
harvnb
Libbrecht
[12]
harvnb
Horner
[13]
harvnb
Fuller
[14]
harvnb
Cajori
[15]
MacTutor
[16]
문서
Analysis Per Quantitatum Series, Fluctiones ac Differentias : Cum Enumeratione Linearum Tertii Ordinis, Londini. Ex Officina Pearsoniana. Anno MDCCXI, p. 10, 4th paragraph.
[17]
문서
Newton's collected papers, the edition 1779, in a footnote, vol. I, p. 270-271
[18]
harvnb
Berggren
[19]
harvnb
Temple
[20]
harvnb
Mikami
[21]
harvnb
Libbrecht
[22]
문서
"Structure and Interpretation of Computer Programs 2nd Edition,"
https://web.mit.edu/[...]
[23]
harvnb
Cormen
[24]
매스월드
Horner's Rule
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com