NAND 게이트

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 기호
3. 논리
4. 하드웨어 기술 및 핀
5. 구현
6. 기능적 완전성
- 6.1. NAND 게이트를 이용한 다른 논리 게이트 구현 (예시)
참조

1. 개요

NAND 게이트는 NOT(a₁ AND a₂ AND ... AND a_n)와 논리적으로 동일한 논리 게이트이다. MIL/ANSI, IEC, DIN 세 가지 기호로 표현되며, ANSI 기호는 표준 AND 게이트에 도치 버블이 연결된 형태이다. NAND 게이트는 TTL 및 CMOS 집적 회로에서 기본 게이트로 사용되며, 4011, 7400 등의 다양한 IC 제품으로 제공된다. NAND 게이트는 NOR 게이트와 함께 기능적으로 완전하여, 다른 모든 논리 함수를 NAND 게이트만으로 구현할 수 있으며, RS 플립플롭과 같은 순차 회로 구현에도 사용된다.

더 읽어볼만한 페이지

논리 게이트 - AND 게이트
AND 게이트는 모든 입력이 참일 때만 참을 출력하고 하나라도 거짓이면 거짓을 출력하는 논리 게이트로, 논리곱으로 표현되며 다양한 방식으로 구현되어 디지털 시스템의 핵심 구성 요소로 사용된다.
논리 게이트 - OR 게이트
OR 게이트는 두 개 이상의 입력 중 하나라도 참이면 출력이 참이 되는 논리 게이트로, 모든 입력이 거짓일 때만 출력이 거짓이 되며 논리합 연산을 수행하고, 다른 게이트들과 함께 부울 회로 구성, 다양한 하드웨어 구현, NAND/NOR 게이트 대체, XOR 게이트와 구별, 진리표/기호 표현, 와이어드 OR 구현 등의 특징을 가진다.
수리논리학 - 셈
셈은 대상의 개수를 파악하는 기본적인 행위로, 수학에서는 집합의 원소 개수를 파악하는 과정으로 정의되며, 셈의 방식에 따라 결과가 달라질 수 있고, 셈을 배우는 과정은 아동의 교육 및 발달에 중요한 역할을 한다.
수리논리학 - 동치
동치는 두 명제가 모든 경우에 동일한 진리값을 가져 논리적으로 같음을 의미하며, 논리학에서는 논리식 단순화 및 변환에 유용한 다양한 논리적 동치(항등, 지배, 멱등, 이중 부정, 교환, 결합, 분배, 드 모르간, 흡수, 부정 법칙 등)가 존재한다.
수학 - 회귀 분석
회귀 분석은 종속 변수와 하나 이상의 독립 변수 간의 관계를 모델링하고 분석하는 통계적 기법으로, 최소 제곱법 개발 이후 골턴의 연구로 '회귀' 용어가 도입되어 다양한 분야에서 예측 및 인과 관계 분석에 활용된다.
수학 - 수학적 최적화
수학적 최적화는 주어진 집합에서 실수 또는 정수 변수를 갖는 함수의 최댓값이나 최솟값을 찾는 문제로, 변수 종류, 제약 조건, 목적 함수 개수에 따라 다양한 분야로 나뉘며 여러 학문 분야에서 활용된다.

NAND 게이트
논리 게이트
NAND 게이트 기호
기본 정보
종류	논리 게이트
입력	2개 이상
출력	1개
논리 연산	NAND 연산
진리표 (2개 입력 기준)	입력 A: 0, 입력 B: 0, 출력: 1 입력 A: 0, 입력 B: 1, 출력: 1 입력 A: 1, 입력 B: 0, 출력: 1 입력 A: 1, 입력 B: 1, 출력: 0
수학적 표현
표기법	NAND(a₁, a₂, ..., aₙ)
다른 표현	NOT(a₁ AND a₂ AND ... AND aₙ)

2. 기호

NAND 게이트는 세 가지 기호로 표현된다. MIL/ANSI 기호, IEC 기호, DIN 기호(현재는 사용이 권장되지 않음)가 있다. NAND 게이트의 ANSI 기호는 표준 AND 게이트에 반전 버블(inversion bubble)이 연결된 형태이다.

기호	설명
MIL/ANSI 기호	MIL/ANSI 기호
IEC 기호	IEC 기호
DIN 기호	DIN 기호 (현재는 사용이 권장되지 않음)

3. 논리

NAND(''a''₁, ''a''₂, ..., ''a_n'') 함수는 NOT(''a''₁ AND ''a''₂ AND ... AND ''a_n'')와 논리적으로 같다.

A NAND B는 $\overline{A \land B}$ 로 표현할 수 있으며, 여기서 ${\land}$ 기호는 AND를, 윗줄은 식의 부정(NOT)을 의미한다. 즉, 간단히 ${\displaystyle \lnot (A \land B)}$ 이다.

4. 하드웨어 기술 및 핀

NAND 게이트는 TTL 및 CMOS IC에서 기본 게이트로 사용된다.^[1]

표준 4000 시리즈 CMOS IC인 4011은 4개의 독립적인 2입력 NAND 게이트를 포함한다. 이 장치는 여러 반도체 제조업체에서 제공하며, 일반적으로 관통형 DIL 및 SOIC 형식으로 제공된다. 데이터시트는 대부분의 데이터시트 데이터베이스에서 쉽게 구할 수 있다.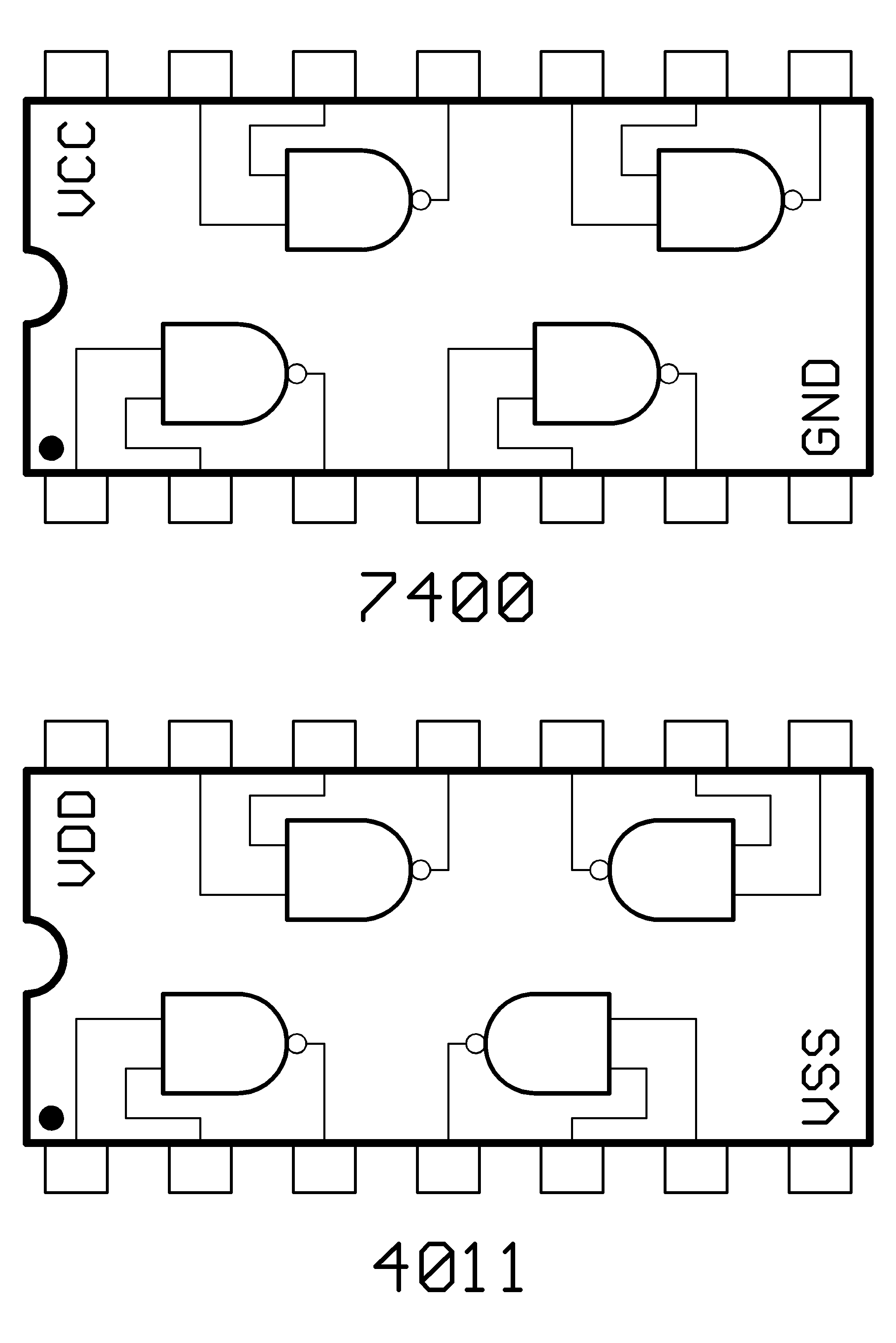

표준 2입력, 3입력, 4입력 및 8입력 NAND 게이트는 다음과 같이 제공된다.

NAND 게이트 IC 종류
CMOS	TTL

NAND 게이트는 범용 논리 IC에서 기본적인 제품으로, 74 시리즈 TTL의 7400, 74HC00 등의 CMOS 버전을 포함하여 여러 가지 변종이 있다.

5. 구현

NAND 게이트는 스위치와 풀업 저항, NMOS, PMOS, CMOS, TTL 등 다양한 방식으로 구현할 수 있다.

NXP반도체가 제조한 74AHC00D 쿼드 2 입력 NAND 게이트의 다이.

기본적인 구현은 스위치 S1 또는 S2 중 하나라도 열려 있으면, 풀업 저항(pull-up resistor) R이 출력 신호 Q를 1(high)로 설정한다. S1과 S2가 모두 닫혀 있으면, 풀업 저항은 스위치에 의해 무시되고 출력은 0(low)이 된다.

디플리션 로드 NMOS 논리(depletion-load NMOS logic) 구현에서, 스위치는 트랜지스터 T2와 T3이고, 트랜지스터 T1은 풀업 저항의 기능을 한다.

CMOS 구현에서, 스위치는 n형 트랜지스터 T3과 T4이고, 풀업 저항은 p형 트랜지스터 T1과 T2로 구성되며, 이는 트랜지스터 T3과 T4의 보수를 형성한다.

CMOS에서 NAND 게이트는 NOR 게이트보다 효율적이다. 이는 p-MOSFET보다 n-MOSFET에서 더 빠른 전하 이동성 때문^[1]이다. 따라서 NAND 게이트에서 구현된 두 개의 p-MOSFET(T1과 T2)의 병렬 연결이 NOR 게이트에서의 직렬 연결보다 유리하다. 이러한 이유로 CMOS 회로에서는 일반적으로 NAND 게이트가 NOR 게이트보다 선호된다.

트랜지스터-트랜지스터 로직(TTL)의 경우, 다수의 에미터를 가진 트랜지스터(멀티 에미터 트랜지스터)를 사용하여 다른 게이트보다 적은 수의 트랜지스터로 구성할 수 있다는 특징이 있으며, 74 시리즈의 첫 번째인 7400이 NAND인 것도 그러한 이유 때문이다. CMOS에서도 특성적으로 불리한 P채널 측이 병렬로, 특성적으로 유리한 N채널 측이 직렬로 구성되므로, 예를 들어 그 반대인 NOR 게이트보다 약간 유리하다.

6. 기능적 완전성

NAND 게이트는 NOR 게이트와 함께 기능적 완전성을 갖는 논리 게이트이다. 즉, NAND 게이트만으로 다른 모든 논리 함수(AND, OR, NOT, XOR 등)를 구현할 수 있다.^[2] 이러한 특성 덕분에 NAND 게이트만으로 복잡한 디지털 회로(예: 프로세서)를 구성할 수 있다.

NOR 논리를 사용하여 NOR 게이트로 NAND 게이트를 만들 수도 있다.^[2]

6. 1. NAND 게이트를 이용한 다른 논리 게이트 구현 (예시)

NAND 게이트는 완전계의 특성을 가지고 있어, NAND 게이트만으로 다른 모든 논리 함수(AND, OR 등)를 구현할 수 있다.^[2] 즉, NAND 게이트만으로 NOT, AND, OR, XOR 등의 기본 논리 회로는 물론, 가산기, 디코더, 인코더 등의 복잡한 조합 회로도 만들 수 있다.

'''NOT 게이트''': 입력 A를 NAND 게이트의 두 입력에 모두 연결하면 NOT A를 얻을 수 있다.
'''AND 게이트''': NAND 게이트의 출력에 NOT 게이트를 연결하면 AND 게이트를 얻을 수 있다.
'''OR 게이트''': 두 개의 NOT 게이트를 각각 NAND 게이트의 입력에 연결하고, 그 출력들을 다시 NAND 게이트에 연결하면 OR 게이트를 얻을 수 있다.

참조

_[1] 웹사이트 Digital circuits, sizing, output impedance, rise and fall time. https://inst.eecs.be[...] 2007-07-06
_[2] 서적 Logic and Computer Design Fundamentals, Third Edition Prentice Hall 2004

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com