NOT 게이트
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
NOT 게이트는 입력 신호를 반전시키는 디지털 논리 게이트이다. 입력이 1이면 0을, 0이면 1을 출력하며, 논리 부정 연산자(¬)와 동일하다. NOT 게이트는 AND, OR 게이트와 함께 모든 부울 회로를 구성하는 데 사용되며, 삼각형 또는 직사각형 모양의 기호로 표시된다. 전자 회로에서는 트랜지스터를 사용하여 구현되며, CMOS 인버터는 전력 소비를 줄이는 데 효과적이다. 또한, NAND 또는 NOR 게이트를 사용하여 NOT 게이트를 만들 수 있으며, 전압 전달 곡선을 통해 성능을 측정한다. CMOS 인버터는 아날로그 선형 증폭기로도 사용될 수 있다.
더 읽어볼만한 페이지
- 논리 게이트 - NAND 게이트
NAND 게이트는 모든 입력이 1일 때 0을 출력하고 그 외에는 1을 출력하는 논리 게이트로서, 다양한 기호로 표현되며, AND 연산의 결과를 부정하는 연산을 수행하고, 여러 방식으로 구현될 수 있으며, 기능적으로 완전하여 디지털 회로 설계에 필수적이다. - 논리 게이트 - AND 게이트
AND 게이트는 모든 입력이 참일 때만 참을 출력하고 하나라도 거짓이면 거짓을 출력하는 논리 게이트로, 논리곱으로 표현되며 다양한 방식으로 구현되어 디지털 시스템의 핵심 구성 요소로 사용된다. - 집적 회로 - 실시간 시계
실시간 시계(RTC)는 CPU 개입 없이 독립적으로 시간을 유지하며, 저전력 소비와 시간 민감 작업의 부담 감소, 절전 모드 유지를 위해 디지털 카운터 회로, 결정 진동자, 배터리 등으로 구성되어 PC 메인보드에 부착되거나 사우스브리지 칩 또는 마이크로컨트롤러에 내장된다. - 집적 회로 - NMOS 논리
NMOS 논리는 n형 MOSFET만을 사용하여 논리 게이트를 구현하는 방식으로, 저항을 부하로 사용하여 NOR 게이트 등을 구현할 수 있지만, Low에서 High로의 전환 속도가 느리고 전력 소비가 높아 CMOS 논리에 밀려 현재는 제한적으로 사용된다. - 표시 이름과 문서 제목이 같은 위키공용분류 - 라우토카
라우토카는 피지 비치레부섬 서부에 위치한 피지에서 두 번째로 큰 도시이자 서부 지방의 행정 중심지로, 사탕수수 산업이 발달하여 "설탕 도시"로 알려져 있으며, 인도에서 온 계약 노동자들의 거주와 미 해군 기지 건설의 역사를 가지고 있고, 피지 산업 생산의 상당 부분을 담당하는 주요 기관들이 위치해 있다. - 표시 이름과 문서 제목이 같은 위키공용분류 - 코코넛
코코넛은 코코넛 야자나무의 열매로 식용 및 유지로 사용되며, 조리되지 않은 과육은 100g당 354kcal의 열량을 내는 다양한 영양 성분으로 구성되어 있고, 코코넛 파우더의 식이섬유는 대부분 불용성 식이섬유인 셀룰로오스이며, 태국 일부 지역에서는 코코넛 수확에 훈련된 원숭이를 이용하는 동물 학대 문제가 있다.
| NOT 게이트 | |
|---|---|
| 기본 정보 | |
 | |
| 종류 | 논리 게이트 |
| 표준 | IEC 60617-12 |
| 기능 | 논리적 부정(NOT) |
| 진리표 입력 | A |
| 진리표 출력 | Q = ¬A |
| 논리식 | Q = ¬A |
| 구현 | |
| 소자 | 바이폴라 접합 트랜지스터 전계효과 트랜지스터 저항 |
| 패키지 | 집적 회로 |
| 사용 예시 | CMOS TTL |
| 관련 정보 | |
| 관련 게이트 | AND 게이트 OR 게이트 NAND 게이트 NOR 게이트 XOR 게이트 XNOR 게이트 |
2. 설명
NOT 게이트는 1이 입력되면 0을 출력하고, 0이 입력되면 1을 출력한다. 따라서 입력값을 반전시킨다. 일반적으로 비트의 이러한 반전을 "플리핑(flipping)"이라고 부른다.[1] 1과 0 대신 참과 거짓, 또는 높음과 낮음과 같은 다른 기호 쌍을 사용할 수 있다.
이는 수리 논리의 논리 부정 연산자(¬)와 동일하다. 입력이 하나뿐이므로 단항 연산이며 가장 단순한 형태의 진리표를 갖는다. 또한 0과 1을 바꾸어 이진수의 1의 보수를 생성하기 때문에 보수 게이트라고도 한다.[2]
NOT 게이트는 AND 게이트, OR 게이트와 함께 모든 부울 회로를 구성할 수 있는 세 가지 기본 논리 게이트 중 하나이다. 이 세 가지 게이트로 이진 수학의 모든 함수를 구현할 수 있으며, 다른 모든 논리 게이트는 이 세 가지 게이트로 만들 수 있다.[3]
"프로그래밍 가능 반전기" 또는 "제어 반전기"라는 용어는 NOT 게이트가 아니라 XOR 게이트를 지칭한다. XOR 게이트는 NOT 게이트처럼 조건부로 작동할 수 있기 때문이다.[1][3]
| NOT 게이트 진리표 | |
|---|---|
| 입력 | 출력 |
| 0 | 1 |
| 1 | 0 |
NOT 게이트는 0이 입력되면 1을, 1이 입력되면 0을 출력하여 입력값을 반전시킨다. 이러한 동작은 "플리핑(flipping)"이라고도 불린다.[1] 참과 거짓, 높음과 낮음 등 다른 기호 쌍을 1과 0 대신 사용할 수 있다.
3. 심볼
인버터 회로의 전통적인 기호는 작은 원("버블")에 닿는 삼각형이다. 입력 및 출력 라인이 기호에 부착된다. 버블은 일반적으로 출력 라인에 부착된다. 액티브 로우 입력을 나타내기 위해 때로는 버블이 대신 입력 라인에 배치된다.[4] 때로는 기호의 원 부분만 사용되며 다른 게이트의 입력 또는 출력에 부착된다. NAND 및 NOR의 기호는 이런 방식으로 형성된다.[3]
변수 위에 가로 막대 또는 오버라인 ( ‾ )은 NOT 게이트에 의해 수행되는 부정(또는 반전 또는 보수)을 나타낼 수 있다.[4] 변수 앞에 슬래시(/)가 사용되기도 한다.[3]
NOT 게이트를 나타내는 기호는 3종류(ANSI, IEC, DIN)가 있다.ANSI 기호 IEC 기호 DIN 기호 -- -- --
4. 회로 및 동작
NOT 게이트는 수리 논리에서 논리 부정(¬) 연산자와 같으며, 입력이 하나뿐이므로 단항 연산이다. 가장 단순한 진리표를 가지며, 이진수의 1의 보수를 만들기 때문에 보수 게이트라고도 불린다.[2]
AND 게이트, OR 게이트와 함께 NOT 게이트는 모든 부울 회로를 구성할 수 있는 세 가지 기본 논리 게이트 중 하나이다. 이 세 가지 게이트로 이진 수학의 모든 함수를 구현할 수 있고, 다른 모든 논리 게이트도 이 세 가지 게이트로 만들 수 있다.[3]
디지털 회로는 논리 0과 1에 해당하는 고정된 전압 레벨에서 작동하며, NOT 게이트는 이 두 전압 레벨을 바꾸는 기본 논리 게이트 역할을 한다. 구현에 따라 실제 전압은 다르지만, TTL 회로에서는 보통 0V와 +5V가 사용된다.NOT 게이트 진리표 입력 (A) 출력 (NOT A) 0 1 1 0
4. 1. 전자 회로 구현
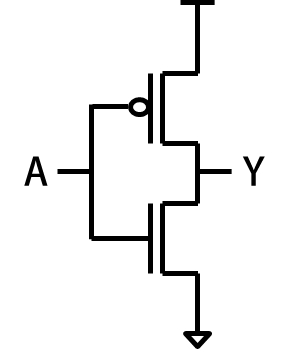
A에 0이 인가되면 PMOS가 켜지고(Turn-on) VDD로부터 전류가 흘러 Y에 전하를 축적시키며 1의 출력값을 갖는다. 반대로 A에 1이 인가되면 NMOS가 켜지고 축적된 전하가 GND로 빠져나가 0의 출력값을 갖는다.
인버터 회로는 입력의 반대 논리 레벨을 나타내는 전압을 출력한다. 즉, 입력 신호를 반전시키는 기능을 수행한다. 입력이 낮으면(0) 출력은 높아지고(1), 입력이 높으면(1) 출력은 낮아진다(0).
인버터는 NMOS 트랜지스터 하나와 저항을 결합하거나, PMOS 트랜지스터 하나와 저항을 결합하여 구성할 수 있다. 이러한 "저항 드레인" 방식은 한 종류의 트랜지스터만 사용하므로 제작 비용이 저렴하다. 그러나 저항을 통해 항상 전류가 흐르기 때문에 전력 소비가 크고 처리 속도가 느리다는 단점이 있다.
CMOS 구성은 두 개의 상보적인 트랜지스터(NMOS와 PMOS)를 사용하여 인버터를 구현한다. 이 방식은 두 논리 상태 중 항상 하나의 트랜지스터만 켜지므로 전력 소비를 크게 줄일 수 있다.[5] 또한, NMOS 또는 PMOS만 사용한 방식에 비해 저항이 낮아 처리 속도도 향상된다.
인버터는 저항-트랜지스터 로직(RTL) 또는 트랜지스터-트랜지스터 로직(TTL) 구성에서 바이폴라 접합 트랜지스터(BJT)를 사용하여 구성할 수도 있다.
4. 2. 디지털 구성 요소
반전기는 디지털 전자 공학의 기본적인 구성 요소이다. 멀티플렉서, 디코더, 상태 기계 등 다양한 디지털 장치에 사용된다.
헥스 반전기는 6개의 반전기를 포함하는 집적 회로이다. 예를 들어 14핀 7404 TTL 칩과 16핀 CMOS 4049 칩이 있는데, 이 중 2개는 전원/참조용으로, 12개는 6개 반전기의 입출력용으로 사용된다(4049는 2개의 미사용 핀이 있다).
4. 2. 1. 분석적 표현
NOT gate영어의 해석적 표현은 다음과 같다.[1]
:
5. 대안
특정 NOT 게이트를 사용할 수 없는 경우, 범용 NAND 게이트 또는 NOR 게이트[6]를 사용하여 NOT 게이트를 구현할 수 있다. XOR 게이트의 한쪽 입력을 High로 설정하여 NOT 게이트처럼 동작하게 할 수도 있다.
| 원하는 게이트 | NAND 구성 | NOR 구성 |
|---|---|---|
 | -- |  |
6. 성능 측정
디지털 인버터의 품질은 출력 전압 대 입력 전압의 그래프인 전압 전달 곡선(VTC)을 사용하여 측정하는 경우가 많다. 이러한 그래프에서 잡음 내성, 이득 및 작동 논리 레벨을 포함한 장치 매개변수를 얻을 수 있다.[1]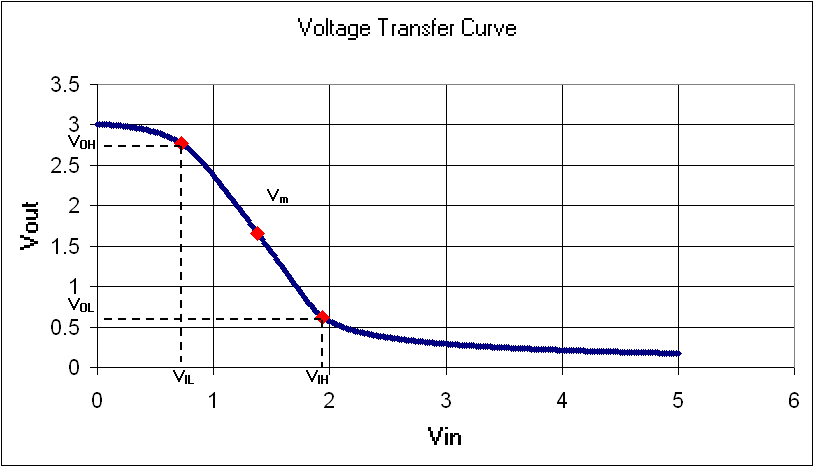
이상적으로 VTC는 반전된 계단 함수 형태로 나타난다. 이는 "켜짐"과 "꺼짐" 사이의 정확한 전환을 나타내지만, 실제 장치에서는 점진적인 전환 영역이 존재한다. VTC는 낮은 입력 전압의 경우 회로가 높은 전압을 출력하고, 높은 입력의 경우 출력이 낮은 레벨로 감소함을 나타낸다. 이 전환 영역의 기울기는 품질의 척도이며, 가파른(수직에 가까운) 기울기는 정확한 전환을 생성한다.[1]
잡음에 대한 내성은 각 작동 영역(켜짐/꺼짐)에 대해 최소 입력과 최대 출력을 비교하여 측정할 수 있다.[1]
7. 아날로그적 이용
CMOS 인버터 디지털 논리 게이트는 전이 영역이 가파르고 대략 선형이므로, 적절하게 바이어스하면 고이득 아날로그 선형 증폭기로 사용할 수 있다.[7][8][9][10][11] 여러 개의 NOT 게이트를 결합하여 연산 증폭기를 구성할 수도 있다.[12] 최대 이득은 입력과 출력 동작점이 동일한 전압일 때 달성되며, 이는 출력과 입력 사이에 저항을 연결하여 바이어스할 수 있다.[13]
NOT 게이트는 아날로그적으로 보면 반전 증폭기 또는 반전 버퍼로 동작한다. 하지만 이는 보장된 이용법은 아니며, 내부 소자의 임계값, 전원 전압, 입력 전위 관계에 따라 관통 전류가 흐를 가능성도 있으므로 주의가 필요하다. 이러한 NOT 게이트의 아날로그적 특성을 이용한 전자공작 사례가 종종 보인다.
참조
[1]
서적
Crypto 101
https://github.com/c[...]
[2]
웹사이트
2.9 Digital Logic Gates
https://www.uobabylo[...]
[3]
서적
Practical Programmable Circuits: A Guide to PLDs, State Machines, and Microcontrollers
https://books.google[...]
Elsevier Science
[4]
웹사이트
Logic NOT Gate Tutorial
https://www.electron[...]
2013-08-20
[5]
서적
Digital electronics and logic design
https://books.google[...]
PHI Learning Pvt. Ltd.
2002
[6]
서적
Logic and computer design fundamentals
https://books.google[...]
Prentice Hall
2004
[7]
웹사이트
Application Note 88: CMOS Linear Applications
https://www.elektron[...]
2003-04-00
[8]
웹사이트
CMOS gate as linear amplifier
http://melbmcu.weebl[...]
2023-05-18
[9]
Youtube
CMOS Inverters as Analog Amplifiers (Adventures in Field Programmable Analog Arrays)
https://www.youtube.[...]
2023-05-18
[10]
웹사이트
CMOS-Inverter-as-an-Amplifier Analog-CMOS-Design Electronics Tutorial
https://www.electron[...]
2023-05-18
[11]
웹사이트
Activity: CMOS Amplifier stages - ADALM2000 [Analog Devices Wiki]
https://wiki.analog.[...]
2023-05-18
[12]
웹사이트
A true op-amp made from inverters
https://www.edn.com/[...]
2023-05-18
[13]
학술지
CMOS Inverter as Analog Circuit: An Overview
2019-09-20
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com

