맨위로가기

그래프 신경망

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

그래프 신경망(GNN)은 그래프 구조의 데이터를 처리하기 위한 인공 신경망의 한 종류이다. GNN은 순열 등변성, 지역 풀링, 전역 풀링 등의 아키텍처를 가지며, 메시지 전달 층을 통해 노드 간의 정보 교환을 구현한다. GNN은 Weisfeiler-Leman 그래프 동형성 테스트보다 표현력이 제한적일 수 있지만, 다양한 분야에서 응용되고 있다. 주요 모델로는 그래프 컨볼루션 네트워크(GCN), 그래프 어텐션 네트워크(GAT), 게이티드 그래프 시퀀스 신경망(GGS-NN) 등이 있다. GNN은 생명 과학, 소셜 네트워크 분석, 조합 최적화, 사이버 보안, 수도 시스템 등 다양한 분야에 활용된다.

2. 아키텍처

일반적인 GNN의 아키텍처는 다음과 같은 기본적인 층을 구현한다:[25]


  • 순열 등변성(Permutation equivariant)
  • 지역 풀링(Local pooling)
  • 전역 풀링(Global pooling): 'readout' 층이라고도 한다.


GNN은 Weisfeiler-Leman 그래프 동형성 테스트보다 더 표현력이 있을 수 없다는 것이 입증되었다.[26][27] 이는 GNN으로 구별할 수 없는 서로 다른 그래프 구조(예: 동일한 원자를 가지지만 다른 화학 결합을 갖는 분자)가 존재한다는 것을 의미한다. 단순 복합체와 같은 고차원 기하학에서 작동하는 더 강력한 GNN을 설계할 수 있다.[32][49] 미래 아키텍처가 메시지 전달 기본 요소를 극복할 수 있을지는 열린 연구 문제이다.[28]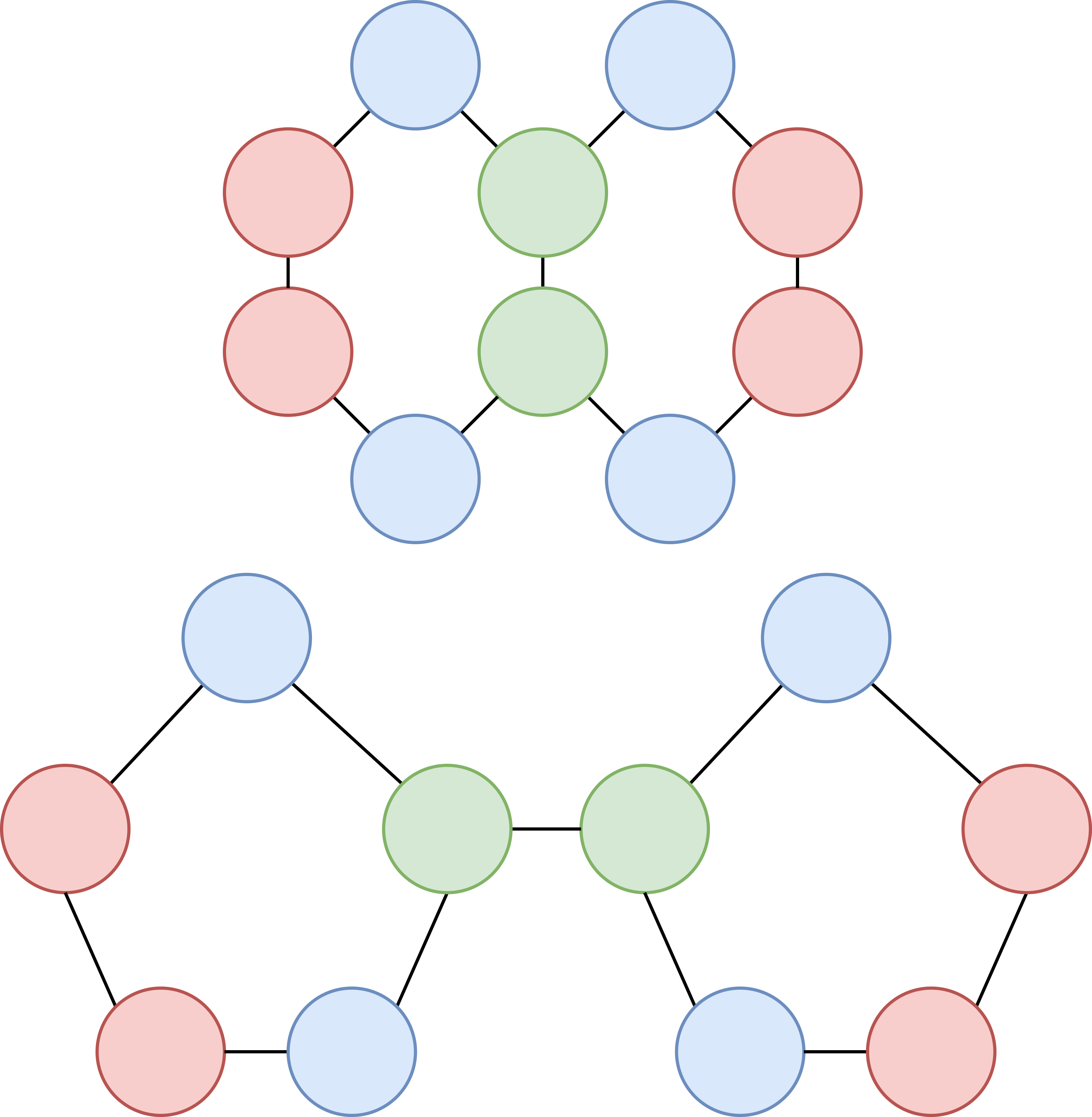

비동형 그래프는 Weisfeiler-Lehman 그래프 동형성 테스트의 제한으로 인해 GNN으로 구별할 수 없다. 색상은 노드 특징을 나타낸다.

2. 1. 순열 등변성(Permutation Equivariant) 층

순열 등변성 층은 그래프의 표현을 동일한 그래프의 업데이트된 표현으로 사상한다. 문헌에서 순열 등변성 층은 그래프 노드 간의 쌍별 메시지 전달을 통해 구현된다.[25][28] 직관적으로, 메시지 전달 층에서 노드는 바로 이웃한 노드로부터 받은 *메시지*를 *집계*하여 자신의 표현을 *업데이트*한다. 따라서 각 메시지 전달 층은 GNN의 수용 필드를 홉 단위로 증가시킨다.

2. 2. 지역 풀링(Local Pooling) 층

지역 풀링 층은 다운샘플링을 통해 그래프를 더 작은 규모로 만든다. 이는 컨볼루션 신경망의 풀링 층과 유사한 역할을 한다.[25] k-최근접 이웃 풀링, Top-k 풀링,[33] Self-attention 풀링[34] 등이 있다.

Top-k 풀링과 Self-attention 풀링 방법에 대해 알아보자.[30] 각 경우, 입력은 노드 특징의 행렬 \mathbf{X}와 그래프 인접 행렬 \mathbf{A}로 표현된 초기 그래프이다. 출력은 노드 특징의 새로운 행렬 \mathbf{X}'와 새로운 그래프 인접 행렬 \mathbf{A}'이다.

먼저, 학습 가능한 사영 벡터 \mathbf{p}를 설정하여 각 그래프 노드에 대한 스칼라 사영 값을 계산한다.

:\mathbf{y} = \frac{\mathbf{X}\mathbf{p}}{\Vert\mathbf{p}\Vert}

Top-k 풀링 층[33]은 다음과 같이 계산된다.

:\mathbf{X}' = (\mathbf{X} \odot \text{sigmoid}(\mathbf{y}))_{\mathbf{i}}

:\mathbf{A}' = \mathbf{A}_{\mathbf{i}, \mathbf{i}}

여기서 \mathbf{i} = \text{top}_k(\mathbf{y})는 가장 높은 Top-k 사영 점수를 가진 노드의 부분 집합을 나타내고, \odot는 원소별 행렬 곱셈을 나타내며, \text{sigmoid}(\cdot)는 시그모이드 함수이다. 가장 높은 Top-k 사영 점수를 가진 노드는 새로운 인접 행렬 \mathbf{A}'에 유지된다. \text{sigmoid}(\cdot) 연산은 사영 벡터 \mathbf{p}를 역전파를 통해 학습 가능하게 한다.[33]

Self-attention 풀링 층[34]을 계산하기 위해, 먼저 일반적인 순열 등변 GNN 층(예: GCN, GAT, MPNN)을 설정한다.

:\mathbf{y} = \text{GNN}(\mathbf{X}, \mathbf{A})

Self-attention 풀링 층은 다음과 같이 공식화될 수 있다.

:\mathbf{X}' = (\mathbf{X} \odot \mathbf{y})_{\mathbf{i}}

:\mathbf{A}' = \mathbf{A}_{\mathbf{i}, \mathbf{i}}

여기서 \mathbf{i} = \text{top}_k(\mathbf{y})는 투영 점수가 가장 높은 상위 k개 노드의 하위 집합을 나타내고, \odot는 원소별 행렬 곱셈을 나타낸다.

Self-attention 풀링 층은 Top-k 풀링 층의 확장으로 볼 수 있다. Top-k 풀링과 달리 Self-attention 풀링에서 계산된 Self-attention 점수는 그래프 특징과 그래프 토폴로지를 모두 고려한다.

2. 3. 전역 풀링(Global Pooling) 층

''readout'' 층이라고도 하는 전역 풀링 층은 전체 그래프의 고정 크기 표현을 제공한다. 전역 풀링 층은 순열 불변성을 가져야 하며, 그래프 노드 및 엣지의 순서 변경이 최종 출력에 영향을 미치지 않아야 한다.[30] 예로는 요소별 합계, 평균 또는 최댓값이 있다.

3. 메시지 전달 층

메시지 전달 층은 그래프를 동일 그래프의 업데이트된 표현으로 매핑하는 순열 등변 레이어이다. 이는 메시지 전달 신경망(MPNN)으로 표현할 수 있다.[25]

MPNN 레이어의 출력은 그래프의 각 노드 u \in V에 대한 노드 표현 \mathbf{h}_u이며, 이는 노드/그래프 분류 또는 에지 예측과 같은 다운스트림 작업에 사용될 수 있다.

MPNN에서 그래프 노드는 직접적인 이웃으로부터 정보를 집계하여 표현을 업데이트한다. n개의 MPNN 레이어를 쌓으면 하나의 노드가 최대 n "홉" 떨어진 노드와 통신할 수 있다. 모든 노드가 다른 모든 노드로부터 정보를 받도록 하려면 그래프 지름과 동일한 수의 MPNN 레이어를 쌓아야 한다.

MPNN의 기본 공식, 과도한 스무딩 및 과도한 압착 문제, 주요 모델(GCN, GAT, GGS-NN)에 대한 자세한 내용은 하위 섹션을 참조할 수 있다.

3. 1. 기본 공식

G = (V,E)를 그래프라고 하자. 여기서 V는 노드 집합이고 E는 에지 집합이다. N_u를 노드 u \in V의 이웃이라고 하자. 또한, \mathbf{x}_u를 노드 u \in V의 특징이라고 하고, \mathbf{e}_{uv}를 에지 (u, v) \in E의 특징이라고 하자. 메시지 전달 신경망(MPNN) 레이어는 다음과 같이 표현할 수 있다.[25]

:\mathbf{h}_u = \phi \left( \mathbf{x}_u, \bigoplus_{v \in N_u} \psi(\mathbf{x}_u, \mathbf{x}_v, \mathbf{e}_{uv}) \right)

여기서 \phi와 \psi는 미분 가능한 함수 (예: 인공 신경망)이고, \bigoplus는 임의의 수의 입력을 수용할 수 있는 순열 불변량 집계 연산자이다 (예: 요소별 합계, 평균 또는 최대). 특히, \phi와 \psi는 각각 '업데이트' 및 '메시지' 함수라고 한다. 직관적으로, MPNN 계산 블록에서 그래프 노드는 이웃으로부터 수신한 '메시지'를 '집계'하여 표현을 '업데이트'한다.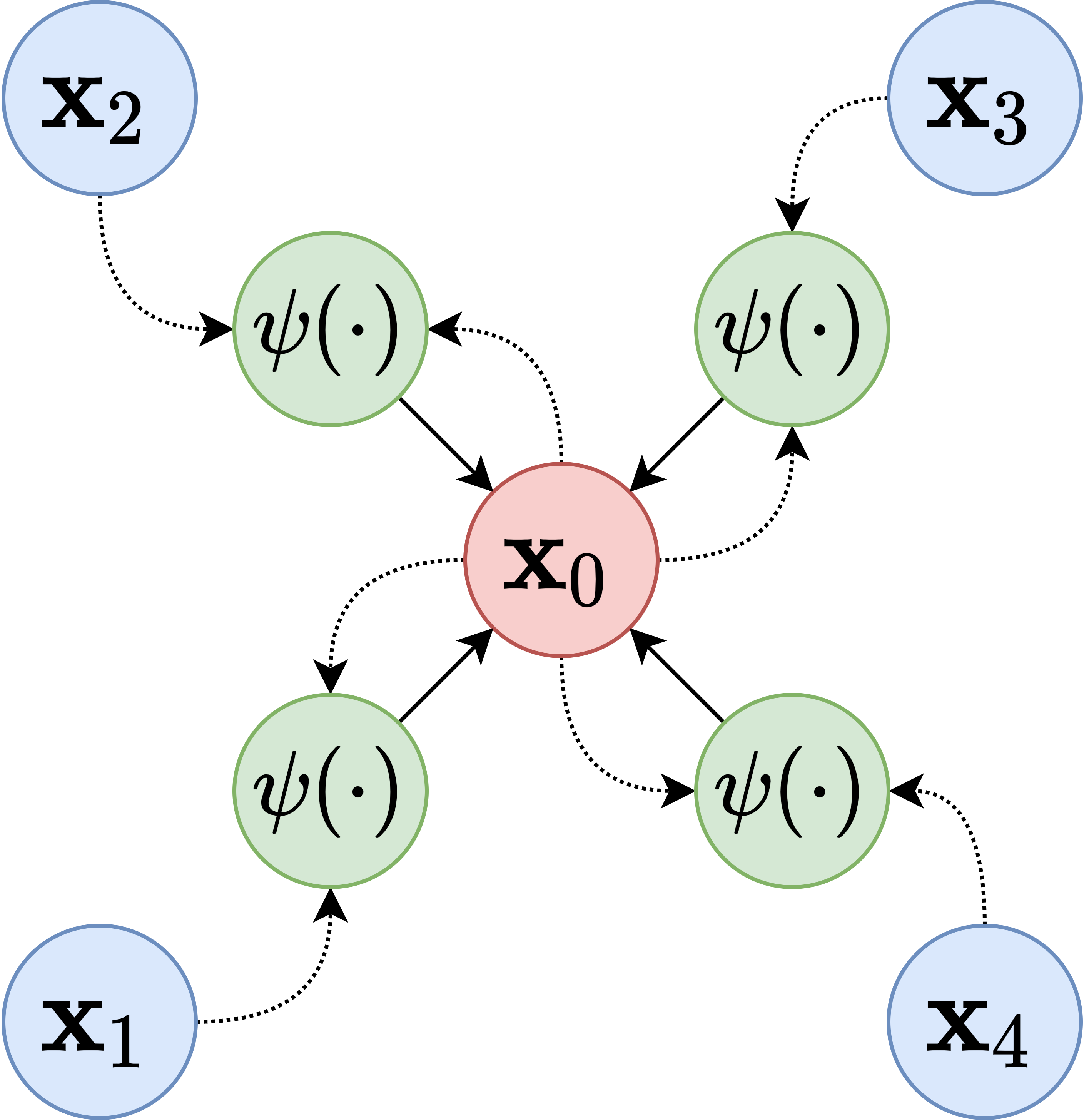

메시지 전달 신경망(MPNN) 레이어에서 노드 표현 업데이트. 노드 \mathbf{x}_0은 모든 직접적인 이웃 \mathbf{x}_1에서 \mathbf{x}_4까지 전송된 메시지를 수신한다. 메시지는 송신자와 수신자의 특징을 모두 고려하는 메시지 함수 \psi를 통해 계산된다.

3. 2. 과도한 스무딩 및 과도한 압착 문제

여러 층의 메시지 전달 신경망(MPNN)을 쌓으면 과도한 스무딩(oversmoothing)[36] 및 과도한 압착(over-squashing)[35]과 같은 문제가 발생할 수 있다.

  • 과도한 스무딩: 노드 표현이 서로 구별할 수 없게 되는 현상이다.[36]
  • 과도한 압착: 장거리 의존성을 고정 크기 표현으로 압축하면서 발생하는 병목 현상이다.[35]


이러한 문제를 완화하기 위한 해결책은 다음과 같다.

  • 잔차 신경망과 유사한 스킵 연결(skip connection)[21][47]
  • 게이트 업데이트 규칙[48]
  • 점핑 지식(jumping knowledge)[50]
  • 마지막 레이어를 완전 인접 레이어(fully-adjacent layer)로 수정. 즉, 그래프를 완전 그래프로 간주하여 장거리 의존성이 필요한 문제에서 과도한 압착을 완화[35]

3. 3. 주요 모델

그래프 신경망의 주요 모델로는 그래프 컨볼루션 네트워크 (GCN), 그래프 어텐션 네트워크 (GAT), 게이티드 그래프 시퀀스 신경망 (GGS-NN) 등이 있다. GCN은 토마스 키프와 맥스 웰링이, GAT는 페타르 벨리치코비치 등이, GGS-NN은 위자 리 등이 소개했다. 각 모델에 대한 자세한 내용은 하위 섹션을 참조하면 된다.

3. 3. 1. 그래프 컨볼루션 네트워크 (GCN, Graph Convolutional Network)

그래프 컨볼루션 네트워크(GCN, Graph Convolutional Network)는 2017년 토마스 키프(Thomas Kipf)와 맥스 웰링(Max Welling)에 의해 처음 소개되었다.[20]

GCN은 컨볼루션 신경망을 그래프 구조 데이터로 일반화한 것으로, 그래프에 대한 국소적 스펙트럼 필터의 1차 근사를 정의한다.

GCN 레이어의 공식 표현은 다음과 같다.

:\mathbf{H} = \sigma\left(\tilde{\mathbf{D}}^{-\frac{1}{2}} \tilde{\mathbf{A}} \tilde{\mathbf{D}}^{-\frac{1}{2}} \mathbf{X} \mathbf{\Theta}\right)

여기서 각 항목은 다음과 같다.

  • \mathbf{H} : 노드 표현 \mathbf{h}_u의 행렬
  • \mathbf{X} : 노드 특징 \mathbf{x}_u의 행렬
  • \sigma(\cdot) : 활성 함수 (예: ReLU)
  • \tilde{\mathbf{A}} : 자기 루프가 추가된 그래프 인접 행렬
  • \tilde{\mathbf{D}} : 자기 루프가 추가된 그래프 차수 행렬
  • \mathbf{\Theta} : 학습 가능한 매개변수의 행렬


특히, \mathbf{A}를 그래프 인접 행렬이라고 하면, \tilde{\mathbf{A}} = \mathbf{A} + \mathbf{I} 및 \tilde{\mathbf{D}}_{ii} = \sum_{j \in V} \tilde{A}_{ij}로 정의할 수 있으며, 여기서 \mathbf{I}는 항등 행렬을 나타낸다. 이 정규화는 \tilde{\mathbf{D}}^{-\frac{1}{2}} \tilde{\mathbf{A}} \tilde{\mathbf{D}}^{-\frac{1}{2}}의 고유값이 [0, 1] 범위 내에 있도록 보장하여, 수치적 안정성 문제를 피하고 기울기 폭주/소실을 방지한다.

GCN의 한계는 다차원 에지 특징 \mathbf{e}_{uv}을 허용하지 않는다는 것이다.[20] 그러나 A_{uv} = w_{uv}를 적용하여, 즉 인접 행렬의 각 0이 아닌 항목을 해당 에지의 가중치로 설정하여, 각 에지에 스칼라 가중치 w_{uv}를 연결하는 것은 가능하다.

3. 3. 2. 그래프 어텐션 네트워크 (GAT, Graph Attention Network)

페타르 벨리치코비치 등이 2018년에 소개하였다.[22]

그래프 신경망과 어텐션 레이어를 결합한 것이다. 그래프 신경망에서 어텐션 레이어를 구현하면 전체 데이터에 집중하는 대신 데이터에서 중요한 정보에 어텐션 또는 초점을 맞출 수 있다.

멀티 헤드 GAT 레이어는 다음과 같이 표현할 수 있다.

: \mathbf{h}_u = \overset{K}{\underset{k=1}{\Big\Vert}} \sigma \left(\sum_{v \in N_u} \alpha_{uv} \mathbf{W}^k \mathbf{x}_v\right)

여기서 K는 어텐션 헤드의 수이고, \Big\Vert는 벡터 연결을 나타내며, \sigma(\cdot)는 활성 함수 (예: ReLU)이고, \alpha_{ij}는 어텐션 계수이며, W^k는 k번째 어텐션 헤드에 대한 학습 가능한 매개변수의 행렬이다.

최종 GAT 레이어의 경우, 활성 함수를 적용하기 전에 각 어텐션 헤드의 출력이 평균화된다. 공식적으로, 최종 GAT 레이어는 다음과 같이 쓸 수 있다.

: \mathbf{h}_u = \sigma \left(\frac{1}{K}\sum_{k=1}^K \sum_{v \in N_u} \alpha_{uv} \mathbf{W}^k \mathbf{x}_v\right)

머신 러닝에서의 어텐션은 인지적 어텐션을 모방하는 기술이다. 그래프 학습의 맥락에서 어텐션 계수 \alpha_{uv}는 노드 v \in V에 대해 노드 u \in V가 ''얼마나 중요한지''를 측정한다.

정규화된 어텐션 계수는 다음과 같이 계산된다.

:\alpha_{uv} = \frac{\exp(\text{LeakyReLU}\left(\mathbf{a}^T [\mathbf{W} \mathbf{x}_u \Vert \mathbf{W} \mathbf{x}_v \Vert \mathbf{e}_{uv}]\right))}{\sum_{z \in N_u}\exp(\text{LeakyReLU}\left(\mathbf{a}^T [\mathbf{W} \mathbf{x}_u \Vert \mathbf{W} \mathbf{x}_z \Vert \mathbf{e}_{uz}]\right))}

여기서 \mathbf{a}는 학습 가능한 가중치의 벡터이고, \cdot^T는 전치를 나타내며, \mathbf{e}_{uv}는 엣지 특징(있는 경우)이며, \text{LeakyReLU}는 수정된 ReLU 활성 함수이다. 어텐션 계수는 다른 노드 간에 쉽게 비교할 수 있도록 정규화된다.[22]

GCN은 어텐션 계수가 학습 가능하지 않고 고정되어 있으며 엣지 가중치 w_{uv}와 동일한 GAT의 특수한 경우로 볼 수 있다.

3. 3. 3. 게이티드 그래프 시퀀스 신경망 (GGS-NN, Gated Graph Sequence Neural Network)

위자 리 등에 의해 2015년에 소개된[48] 게이티드 그래프 시퀀스 신경망(GGS-NN)은 Scarselli 등의 GNN 공식을 확장하여 시퀀스를 출력한다.[15] 메시지 전달 프레임워크는 게이티드 순환 유닛(GRU) 셀에 대한 업데이트 규칙으로 구현된다.

GGS-NN은 다음과 같이 표현할 수 있다.

:\mathbf{h}_u^{(0)} = \mathbf{x}_u \, \Vert \, \mathbf{0}

:\mathbf{m}_u^{(l+1)} = \sum_{v \in N_u} \mathbf{\Theta} \mathbf{h}_v

:\mathbf{h}_u^{(l+1)} = \text{GRU}(\mathbf{m}_u^{(l+1)}, \mathbf{h}_u^{(l)})

여기서 \Vert는 벡터 결합을 나타내고, \mathbf{0}은 영벡터이며, \mathbf{\Theta}는 학습 가능한 파라미터 행렬이고, \text{GRU}는 GRU 셀이며, l은 시퀀스 인덱스를 나타낸다. GGS-NN에서 노드 표현은 GRU 셀의 은닉 상태로 간주된다. 초기 노드 특징 \mathbf{x}_u^{(0)}는 GRU 셀의 은닉 상태 차원까지 영으로 채워진다. 동일한 GRU 셀이 각 노드의 표현을 업데이트하는 데 사용된다.

4. 지역 풀링 층

지역 풀링 계층은 다운샘플링을 통해 그래프를 축소한다. 여기서는 몇 가지 학습 가능한 지역 풀링 전략을 제시한다.[30] 각 경우, 입력은 노드 특징의 행렬 \mathbf{X}와 그래프 인접 행렬 \mathbf{A}로 표현된 초기 그래프이고, 출력은 노드 특징의 새로운 행렬 \mathbf{X}'와 새로운 그래프 인접 행렬 \mathbf{A}'이다.

지역 풀링에는 Top-k 풀링과 Self-attention 풀링등이 존재한다. Top-k 풀링은 사영 벡터를 활용하여 각 노드의 사영 값을 계산하고, 가장 높은 Top-k 사영 점수를 가진 노드를 유지한다. Self-attention 풀링은 그래프 특징과 그래프 토폴로지를 모두 고려하여 self-attention 점수를 계산한다.

4. 1. Top-k 풀링

먼저 다음을 설정한다.

:\mathbf{y} = \frac{\mathbf{X}\mathbf{p}}{\Vert\mathbf{p}\Vert}

여기서 \mathbf{p}는 학습 가능한 사영 벡터이다. 사영 벡터 \mathbf{p}는 각 그래프 노드에 대한 스칼라 사영 값을 계산한다.

그런 다음 Top-k 풀링 레이어[33]는 다음과 같이 공식화할 수 있다.

:\mathbf{X}' = (\mathbf{X} \odot \text{sigmoid}(\mathbf{y}))_{\mathbf{i}}

:\mathbf{A}' = \mathbf{A}_{\mathbf{i}, \mathbf{i}}

여기서 \mathbf{i} = \text{top}_k(\mathbf{y})는 가장 높은 Top-k 사영 점수를 가진 노드의 부분 집합을 나타내고, \odot는 원소별 행렬 곱셈을 나타내며, \text{sigmoid}(\cdot)는 시그모이드 함수이다. 즉, 가장 높은 Top-k 사영 점수를 가진 노드는 새로운 인접 행렬 \mathbf{A}'에 유지된다. \text{sigmoid}(\cdot) 연산은 사영 벡터 \mathbf{p}를 역전파를 통해 학습 가능하게 만든다. 그렇지 않으면 이산 출력을 생성할 것이다.[33]

4. 2. Self-attention 풀링

Self-attention 풀링 계층[34]은 다음과 같이 공식화될 수 있다.

:\mathbf{X}' = (\mathbf{X} \odot \mathbf{y})_{\mathbf{i}}

:\mathbf{A}' = \mathbf{A}_{\mathbf{i}, \mathbf{i}}

여기서 \mathbf{i} = \text{top}_k(\mathbf{y})는 투영 점수가 가장 높은 상위 k개 노드의 하위 집합을 나타내고, \odot는 원소별 행렬 곱셈을 나타낸다.

Self-attention 풀링 계층은 top-k 풀링 계층의 확장으로 볼 수 있다. Top-k 풀링과 달리 self-attention 풀링에서 계산된 self-attention 점수는 그래프 특징과 그래프 토폴로지를 모두 고려한다.[30]

5. 응용 분야

그래프 신경망(GNN)은 여러 분야에 응용된다. 생물학 분야에서는 단백질 접힘 문제를 해결하는 알파폴드 개발에 쓰였고,[37][38][50] 소셜 네트워크 분석, 추천 시스템 개발에도 활용된다.[39][40] GNN은 조합 최적화 알고리즘의 구성 요소로도 사용되어 최단 경로 문제 해결, 칩 배치 등에 쓰인다.[42][48][43][41] 사이버 보안 분야에서는 컴퓨터 네트워크의 이상 징후를 탐지하여 악성 프로세스를 식별하고, 횡적 이동을 탐지하는 데 사용된다.[8][9][10] 수도 시스템의 수요 예측 및 메타모델 개발에도 GNN이 활용된다.[11][12]

5. 1. 생명 과학

그래프 신경망은 생물학의 단백질 접힘 문제를 해결하기 위해 구글의 딥마인드가 개발한 인공지능 프로그램인 알파폴드의 주요 구성 요소 중 하나이다. 알파폴드는 여러 CASP 대회에서 1위를 차지했다.[37][38][50]

5. 2. 소셜 네트워크 분석

소셜 네트워크는 소셜 그래프로 자연스럽게 표현되기 때문에 그래프 신경망(GNN)의 주요 응용 분야이다. GNN은 사회적 관계와 항목 관계를 기반으로 추천 시스템을 개발하는 데 사용된다.[39][40]

5. 3. 조합 최적화

그래프 신경망(GNN)은 여러 조합 최적화 알고리즘의 기본 구성 요소로 사용된다.[42] 예시로는 주어진 그래프에 대한 최단 경로 또는 오일러 회로 계산,[48] 수작업으로 만들어진 인간의 해결책보다 우수하거나 경쟁력 있는 칩 배치 도출,[43] 분기 한정법에서 전문적으로 설계된 분기 규칙 개선 등이 있다.[41]

5. 4. 사이버 보안

컴퓨터 네트워크는 그래프로 볼 수 있으며, 그래프 신경망(GNN)을 사용하여 이상 징후를 탐지할 수 있다.[8] 그래프에서 나타나는 이상 징후는 네트워크 내의 악의적인 활동과 관련이 있는 경우가 많다. GNN은 개별 노드[8]와 경로[9]에서 이러한 이상 징후를 식별하여 악성 프로세스를 탐지하는 데 사용된다. 또한, 횡적 이동을 탐지하기 위해 엣지 레벨[10]에서도 GNN이 활용된다.

5. 5. 수도 시스템

수도 시스템도 참고

수도 시스템은 그래프로 모델링될 수 있으며, 이는 GNN의 직접적인 적용이 가능하다. 이러한 종류의 알고리즘은 수요 예측[11]에 적용되어, 예측 능력을 향상시키기 위해 구역 측정 지역을 상호 연결한다. 이 알고리즘을 수도 시스템 모델링에 적용한 또 다른 사례는 메타모델 개발[12]이다.

참조

[1] 논문 A Deep Learning Approach to Antibiotic Discovery https://pubmed.ncbi.[...] 2020-02-20
[2] 간행물 Analyzing Learned Molecular Representations for Property Prediction https://arxiv.org/ab[...] 2024-12-20
[3] 논문 Powerful antibiotics discovered using AI https://www.nature.c[...] 2020-02-20
[4] 논문 HyGAnno: Hybrid graph neural network-based cell type annotation for single-cell ATAC sequencing data https://academic.oup[...] 2024-04-05
[5] 논문 A graph-convolutional neural network model for the prediction of chemical reactivity 2019-01-02
[6] 웹사이트 Deep Graph Library (DGL) https://www.dgl.ai/ 2024-09-12
[7] 간행물 FluxML/GeometricFlux.jl https://github.com/F[...] FluxML 2024-02-03
[8] 논문 Threatrace: Detecting and Tracing Host-Based Threats in Node Level Through Provenance Graph Learning https://ieeexplore.i[...] 2022
[9] 논문 You Are What You Do: Hunting Stealthy Malware via Data Provenance Analysis. 2020
[10] 논문 Euler: Detecting Network Lateral Movement via Scalable Temporal Link Prediction https://www.ndss-sym[...] 2022
[11] 논문 Graph Convolutional Recurrent Neural Networks for Water Demand Forecasting https://agupubs.onli[...] AGU 2024-06-11
[12] 논문 Shall we always use hydraulic models? A graph neural network metamodel for water system calibration and uncertainty assessment https://www.scienced[...] 2024-06-11
[13] 논문 Graph Neural Networks for Natural Language Processing: A Survey https://www.nowpubli[...] 2023
[14] 논문 Graph Neural Networks: Foundations, Frontiers, and Applications https://graph-neural[...] 2022
[15] 논문 The Graph Neural Network Model https://ieeexplore.i[...] 2009
[16] 논문 Neural Network for Graphs: A Contextual Constructive Approach https://ieeexplore.i[...]
[17] 논문 A Gentle Introduction to Graph Neural Networks https://distill.pub/[...] 2021-09-02
[18] 논문 Understanding Convolutions on Graphs https://distill.pub/[...] 2021-09-02
[19] 논문 Neural Message Passing for Quantum Chemistry http://proceedings.m[...] 2017-07-17
[20] 논문 Semi-supervised classification with graph convolutional networks https://ieeexplore.i[...] 2016
[21] 논문 Inductive Representation Learning on Large Graphs https://cs.stanford.[...] 2017
[22] 간행물 Graph Attention Networks 2018-02-04
[23] 웹사이트 Stanford Large Network Dataset Collection https://snap.stanfor[...] 2021-07-05
[24] 논문 Combinatorial optimization with graph convolutional networks and guided tree search 2018
[25] 간행물 Geometric Deep Learning: Grids, Groups, Graphs Geodesics and Gauges 2021-05-04
[26] 간행물 The Weisfeiler–Lehman Method and Graph Isomorphism Testing 2011-01-27
[27] 간행물 How Powerful are Graph Neural Networks? 2019-02-22
[28] 간행물 Message passing all the way up
[29] 논문 Learning representations of irregular particle-detector geometry with distance-weighted graph networks 2019
[30] 간행물 Graph Pooling for Graph Neural Networks: Progress, Challenges, and Opportunities 2022
[31] 간행물 Topological deep learning: Going beyond graph data 2022
[32] 간행물 Weisfeiler and Lehman Go Topological: Message Passing Simplicial Networks 2021
[33] 간행물 Graph U-Nets 2019
[34] 간행물 Self-Attention Graph Pooling 2019
[35] 간행물 On the Bottleneck of Graph Neural Networks and its Practical Implications 2021
[36] 논문 Measuring and Relieving the Over-Smoothing Problem for Graph Neural Networks from the Topological View 2020
[37] 뉴스 Google's DeepMind predicts 3D shapes of proteins https://www.theguard[...] 2020-11-30
[38] 웹사이트 DeepMind's protein-folding AI has solved a 50-year-old grand challenge of biology https://www.technolo[...] 2020-11-30
[39] 서적 Graph Neural Networks for Social Recommendation 2019
[40] 서적 Graph Convolutional Neural Networks for Web-Scale Recommender Systems 2018
[41] 간행물 Exact Combinatorial Optimization with Graph Convolutional Neural Networks 2019
[42] 간행물 Combinatorial optimization and reasoning with graph neural networks
[43] 논문 A graph placement methodology for fast chip design 2021
[44] 간행물 Fast Graph Representation Learning with PyTorch Geometric 2019
[45] 웹사이트 Tensorflow GNN https://github.com/t[...] 2022-06-30
[46] 웹사이트 jraph https://github.com/d[...] 2022-06-30
[47] 간행물 Optimization of Graph Neural Networks: Implicit Acceleration by Skip Connections and More Depth 2021
[48] 간행물 Gated Graph Sequence Neural Networks 2016
[49] 서적 Discrete Calculus: Applied Analysis on Graphs for Computational Science http://leogrady.net/[...] Springer 2011
[50] 간행물 Representation Learning on Graphs with Jumping Knowledge Networks 2018
[51] 웹사이트 GraphNeuralNetworks.jl https://github.com/C[...] 2023-09-21
[52] 저널 HyGAnno: Hybrid graph neural network-based cell type annotation for single-cell ATAC sequencing data 2023-12-01
[53] 저널 A graph-convolutional neural network model for the prediction of chemical reactivity 2019-01-02
[54] 웹인용 GraphNeuralNetworks.jl https://github.com/C[...] 2023-09-21
[55] 인용 FluxML/GeometricFlux.jl https://github.com/F[...] FluxML 2024-02-03


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com