시그모이드 함수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

시그모이드 함수는 실수 값을 입력받아 0과 1 사이의 값을 출력하는 유계, 미분 가능 함수이다. 단조 함수이며, 종 모양의 미분 그래프와 점대칭 그래프를 가지며, 로짓 함수는 시그모이드 함수의 역함수이다. 로지스틱 함수, 쌍곡탄젠트 함수, 아크탄젠트 함수, 오차 함수 등이 시그모이드 함수의 예시이며, 인공 신경망, 통계학, 생물학, 농업, 오디오 신호 처리, 생화학, 컴퓨터 그래픽 등 다양한 분야에서 활용된다.

더 읽어볼만한 페이지

초등 특수 함수 - 지수 함수
지수 함수는 양의 상수 *a*를 밑으로 하는 *y = a^x* 형태의 함수이며, 특히 자연로그의 역함수인 *e^x*는 다양한 정의와 응용을 가지며 복소수로 확장될 수 있다.
초등 특수 함수 - 제곱근
제곱근은 x² = a를 만족하는 x 값으로, a가 양수일 때 두 개의 제곱근을 가지며, 수학, 물리학, 기하학 등 다양한 분야에서 중요한 개념이고, 무리수와도 관련되어 행렬이나 연산자에도 확장된다.
인공신경망 - 인공 뉴런
인공 뉴런은 인공신경망의 기본 요소로서, 입력 신호에 가중치를 곱하고 합산하여 활성화 함수를 거쳐 출력을 생성하며, 생물학적 뉴런을 모방하여 설계되었다.
인공신경망 - 퍼셉트론
퍼셉트론은 프랭크 로젠블랫이 고안한 인공신경망 모델로, 입력 벡터에 가중치를 곱하고 편향을 더한 값을 활성화 함수에 통과시켜 이진 분류를 수행하는 선형 분류기 학습 알고리즘이며, 초기 신경망 연구의 중요한 모델로서 역사적 의미를 가진다.

시그모이드 함수

2. 정의

시그모이드(sigmoid^영어)는 시그모이드 곡선(sigmoid curve^영어)이라고도 하며, 그리스 문자의 시그마(단어 중간에서는 σ^el이지만 여기서는 단어의 마지막 형태인 ς^el를 의미)와 유사한 형태를 띤다는 의미이다. 시그모이드 함수는 모든 실수 입력 값에 대해 정의되고 각 지점에서 음수가 아닌 도함수를 가지며^[3]^[2] 정확히 하나의 변곡점을 갖는 유계, 미분 가능한 실수 함수이다.^[9]

표준 시그모이드 함수는 로짓(logit)의 역함수이며, 통계 처리의 수치 계산 라이브러리에서는 표준 시그모이드 함수를 '''expit''' 함수라고 부르기도 한다.

일반적으로 시그모이드 함수는 <math>(-\infty, \infty) \rightarrow (0,1) </math> 의 단조 증가연속 함수이며, 단 하나의 변곡점을 갖는다. <math>y=0</math> 과 <math>y=1</math> 을 점근선으로 가진다.

<math>x=0</math> 에서 변곡점은 <math>(0,\frac{1}{2})</math> 이다. 시그모이드 함수의 그래프는 <math>(0,\frac{1}{2})</math> 을 중심으로 점대칭이다.

역함수는 로짓 함수로 나타낼 수 있다. 특히, 표준 시그모이드 함수와 로짓 함수는 서로 역함수이다.

도함수와 이계도함수는 시그모이드 함수 자신을 사용하여 간단하게 나타낼 수 있다.

3. 성질

일반적으로 시그모이드 함수는 단조 함수이며, 도함수는 종 모양 함수이다. 연속적이고 음이 아닌 종 모양 함수(국소 최댓값은 하나이며, 퇴화되지 않는 한 국소 최솟값 없음)의 적분은 시그모이드 형태를 띤다. 따라서 많은 일반적인 확률 분포의 누적 분포 함수는 시그모이드 형태이다. 오차 함수는 정규 분포의 누적 분포 함수와 관련이 있으며, 아크탄젠트 함수는 코시 분포의 누적 분포 함수와 관련이 있다.

시그모이드 함수는 x 값이 양 또는 음의 무한대로 갈 때 한 쌍의 수평 점근선에 의해 제한된다. 시그모이드 함수는 특정 값보다 작은 값에서는 볼록 함수이고, 그 값보다 큰 값에서는 오목 함수이다. 예시로 든 많은 경우에서 그 값은 0이다.

$(-\infty, \infty) \rightarrow (0,1)$ 의 단조 증가연속 함수이며, 단 하나의 변곡점을 갖는다.

$y=0$ 과 $y=1$ 을 점근선으로 가지며, 다음이 성립한다.

: $\begin{align}\lim_{x \rightarrow \infty} \varsigma _a (x) &= 1 \\\lim_{x \rightarrow -\infty} \varsigma _a (x) &= 0 \\\lim_{x \rightarrow \pm \infty} \varsigma _a' (x) &= 0\end{align}$

또한, $x=0$ 에서는 다음이 성립한다.

: $\begin{align}\varsigma_a (0) &= \frac{1}{2} \\\varsigma_a' (0) &= \frac{a}{4} \\\varsigma_a'' (0) &= 0\end{align}$

즉, 변곡점은 $(0,\frac{1}{2})$ 이다.

시그모이드 함수의 그래프는 $(0,\frac{1}{2})$ 을 중심으로 점대칭이다. 즉, $\varsigma_a (x) - \frac{1}{2}$ 는 기함수이며, $\varsigma_a (-x) = 1 - \varsigma_a (x)$ 를 만족한다.

역함수는 다음과 같다.

: $\varsigma_a^{-1} (y) = \frac{1}{a} \ln \left( \frac{y}{1-y} \right) = \frac{1}{a} \operatorname{logit} y$

로짓 함수로 나타낼 수 있으며, 표준 시그모이드 함수와 로짓 함수는 서로 역함수이다.

도함수와 이계도함수는 다음과 같다.

: $\begin{align}\varsigma _a' (x) &= \frac{a e^{-ax}}{(1 + e^{-ax} )^2} = a \varsigma_a (x) \{ 1 - \varsigma_a (x) \} \\\varsigma _a'' (x) &= a^2 \varsigma_a (x) \{ 1 - \varsigma_a (x) \} \{ 1 - 2 \varsigma_a (x) \}\end{align}$

시그모이드 함수 자신을 사용하여 간단하게 나타낼 수 있다.

자연 로그와 관련하여 미분하면 다음과 같다.

: $\begin{align}\frac{d}{dx} \ln(\varsigma _a (x)) &= a \varsigma _a (-x) = a (1 - \varsigma_a (x)) \\\frac{d}{dx} \ln(1 - \varsigma _a (x)) &= -a \varsigma _a (x)\end{align}$

4. 여러 가지 시그모이드 함수

여러 시그모이드 함수들의 비교. 모든 함수는 원점에서 기울기가 1이 되도록 정규화되어 있다.

시그모이드 함수는 다양한 종류가 있으며, 각각 다른 특성과 활용 분야를 가진다. 대표적인 예는 다음과 같다:

로지스틱 함수:

:

f(x) = \frac{1}{1 + e^{-x}}

쌍곡탄젠트 (로지스틱 함수를 평행이동하고 상수를 곱한 것과 같음):

:

f(x) = \tanh x = \frac{e^x-e^{-x}}{e^x+e^{-x}}

아크탄젠트 함수:

:

f(x) = \arctan x

오차 함수:

:

f(x) = \operatorname{erf}(x) = \frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2} \, dt

일부 대수함수, 예를 들어:

:

f(x) = \frac{x}{\sqrt{1+x^2}}

^[4]

연속적이고 음이 아닌 "범프 모양" 함수의 적분은 S자형이므로, 많은 일반적인 확률 분포의 누적 분포 함수 역시 S자형이다. 정규 분포의 누적 분포 함수와 관련된 오차 함수가 그 예이다.

4. 1. 로지스틱 함수

가장 대표적인 시그모이드 함수로, 다음 식으로 표현된다.^[4] 통계학, 머신러닝 등 다양한 분야에서 사용된다.

:

f(x) = \frac{1}{1 + e^{-x}}

표준 시그모이드 함수는 로짓(logit)의 역함수이며, 통계 처리의 수치 계산 라이브러리에서는 표준 시그모이드 함수를 '''expit''' 함수라고 부르기도 한다.

로지스틱 함수

:

N = \frac{K}{1 + \exp{r K (t_0 - t)}}

에서

r = a, K = 1, t_0 = 0

으로 했을 경우에 해당한다.

4. 2. 쌍곡탄젠트 함수

쌍곡탄젠트 함수는 로지스틱 함수를 평행이동하고 상수를 곱한 것과 같다. 수식은 다음과 같다.

:

f(x) = \tanh x = \frac{e^x-e^{-x}}{e^x+e^{-x}}

시그모이드 함수는 쌍곡탄젠트 함수를 사용하여 다음과 같이 나타낼 수 있다.

:

\varsigma_a (x) = \frac{\tanh(a x / 2) + 1}{2}

4. 3. 아크탄젠트 함수

:

f(x) = \arctan x

아크탄젠트는 시그모이드 함수의 한 종류이다.

4. 4. 오차 함수

::

f(x) = \operatorname{erf}(x) = \frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2} \, dt

정규 분포의 누적 분포 함수와 관련된 오차 함수는 시그모이드 함수의 한 예이다.^[4]

4. 5. 구데르만 함수

구데르만 함수( Gudermannian function^영어)는 다음과 같이 정의된다.

:

f(x) = \operatorname{gd}(x) = \int_0^x \frac{dt}{\cosh t} = 2\arctan\left(\tanh\left(\frac{x}{2}\right)\right)

이는 시그모이드 함수의 한 종류이다.

4. 6. 일반화 로지스틱 함수

로지스틱 함수

::

f(x) = \frac{1}{1 + e^{-x}}

쌍곡탄젠트 (위의 로지스틱 함수를 평행이동하고 상수를 곱한 것과 같음)

::

f(x) = \tanh x = \frac{e^x-e^{-x}}{e^x+e^{-x}}

아크탄젠트 함수

::

f(x) = \arctan x

오차 함수

::

f(x) = \operatorname{erf}(x) = \frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2} \, dt

일부 대수함수, 예를 들어:

::

f(x) = \frac{x}{\sqrt{1+x^2}}

^[4]

일반화 로지스틱 함수

::

f(x) = \left(1 + e^{-x} \right)^{-\alpha}, \quad \alpha > 0

4. 7. 대수 함수

Algebraic function^영어의 한 예로 다음 식이 있다.

:

f(x) = \frac{x}{\sqrt{1+x^2}}

^[4]

5. 응용

시그모이드 함수는 다양한 분야에서 응용된다.

학습 곡선과 같이, 작은 값에서 시작해 시간이 지남에 따라 가속화하다가 절정에 이르는 자연 현상을 모델링할 때 시그모이드 함수가 사용된다.^[11]^[5]
강산과 강염기 사이의 적정 곡선은 pH 척도의 로그 특성 때문에 시그모이드 형태를 띤다.
로지스틱 함수는 타입 III 유넘을 활용하여 효율적으로 계산할 수 있다.^[7]

5. 1. 인공신경망

인공 신경망에서 시그모이드 함수는 뉴런의 활성화 함수로 사용되어, 입력 신호에 대한 뉴런의 반응을 비선형적으로 조절한다. 과거에는 시그모이드 함수가 주로 사용되었지만, 기울기 소실 문제 등의 단점으로 인해 최근에는 ReLU와 같은 다른 활성화 함수들이 더 많이 사용되는 추세이다.

인공 신경망에서는 효율을 높이기 위해 매끈하지 않은 하드 시그모이드 함수들이 사용되기도 한다. 시그모이드 함수는 미분 함수를 자기 자신으로 간단히 유도할 수 있기 때문에, 미분 성분이 필요한 역전파 알고리즘에 적합하다. 신경망에서 활성 함수 등으로 사용되며, 다차원 버전은 소프트맥스 함수라고 한다.^[7]

5. 2. 통계학

로지스틱 회귀 분석에서 확률 모델을 구축하는 데 로지스틱 함수가 사용된다.^[10]

5. 3. 생물학

학습 곡선과 같은 여러 자연적인 현상은 작은 값에서 시작하여 시간이 지남에 따라 가속화하였다가 절정에 근접하는 모습을 보인다. 구체적인 수학적 모델이 없을 때 시그모이드 함수가 자주 사용된다.^[11]^[5]

반 겐후텐-굽타 모델은 반전된 S-곡선을 기반으로 하며, 작물 수확량의 토양 염도에 대한 반응에 적용된다.

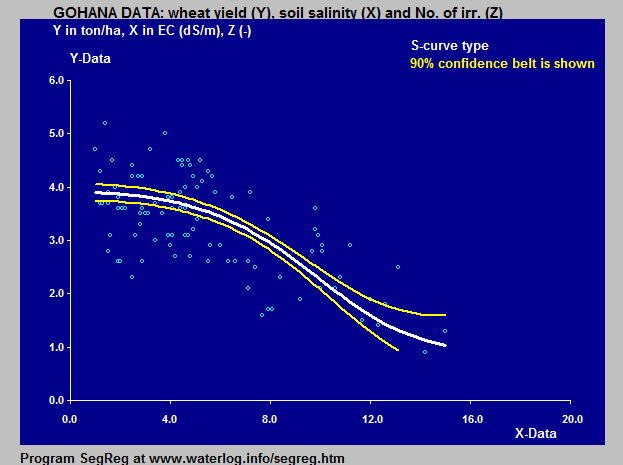
밀 수확량과 토양 염도의 관계를 모델링하기 위한 반전된 로지스틱 S-곡선

작물 수확량(밀)의 토양 염도와 토양 내 지하수위 깊이에 대한 반응에 대한 로지스틱 S-곡선의 적용 예시는 농업에서의 작물 반응 모델링에서 보여진다.^[10]

5. 4. 농업

반 겐후텐-굽타 모델은 반전된 S-곡선을 기반으로 하며, 작물 수확량의 토양 염도에 대한 반응에 적용된다.

작물 수확량(밀)의 토양 염도와 토양 내 지하수위 깊이에 대한 반응에 대한 로지스틱 S-곡선의 적용 예시는 농업에서의 작물 반응 모델링에서 볼 수 있다.

5. 5. 오디오 신호 처리

오디오 신호 처리에서, 시그모이드 함수는 아날로그 회로의 클리핑 소리를 흉내내기 위해 웨이브 셰이퍼 전달 함수로 사용된다.^[6]

5. 6. 생화학 및 약리학

생화학 및 약리학에서, 힐 방정식 및 힐-랭뮤어 방정식은 시그모이드 함수이다.^[5]

5. 7. 컴퓨터 그래픽

컴퓨터 그래픽 및 실시간 렌더링에서, 일부 시그모이드 함수는 두 값 사이의 색상 또는 기하학을 부드럽게 혼합하고, 눈에 보이는 이음새나 불연속성이 없도록 사용된다.

5. 8. 기타

복잡한 시스템의 학습 곡선과 같은 많은 자연 현상은 시간이 지남에 따라 가속화되고 정점에 도달하는 작은 시작점으로부터의 진행을 나타낸다. 특정 수학적 모델이 없을 경우, 시그모이드 함수가 종종 사용된다.^[5]

반 겐후텐-굽타 모델은 반전된 S-곡선을 기반으로 하며, 작물 수확량의 토양 염도에 대한 반응에 적용된다. 작물 수확량(밀)의 토양 염도와 토양 내 지하수위 깊이에 대한 반응에 대한 로지스틱 S-곡선의 적용 예시는 농업에서의 작물 반응 모델링에서 볼 수 있다.

인공 신경망에서, 때로는 효율성을 위해 비매끄러운 함수가 사용되는데, 이를 하드 시그모이드라고 한다.

오디오 신호 처리에서, 시그모이드 함수는 아날로그 회로의 클리핑 사운드를 에뮬레이션하기 위해 웨이브 셰이퍼 전달 함수로 사용된다.^[6]

생화학 및 약리학에서, 힐 및 힐-랭뮤어 방정식은 시그모이드 함수이다.

컴퓨터 그래픽 및 실시간 렌더링에서, 일부 시그모이드 함수는 두 값 사이의 색상 또는 기하학을 부드럽게 혼합하고, 눈에 보이는 이음새나 불연속성이 없도록 사용된다.

강산과 강염기 사이의 적정 곡선은 pH 척도의 로그 특성으로 인해 시그모이드 형태를 갖는다.

로지스틱 함수는 타입 III 유넘을 활용하여 효율적으로 계산할 수 있다.^[7]

참조

_[1] 웹사이트 Smooth Transition Function in One Dimension | Smooth Transition Function Series Part 1 https://www.youtube.[...] 2022-08-16
_[2] 논문 Entropic analysis of biological growth models https://ieeexplore.i[...] 1993-12
_[3] 서적 From Natural to Artificial Neural Computation 1995
_[4] 논문 Some extensions in continuous methods for immunological correlates of protection 2015-12-28
_[5] 논문 Variational Gaussian process classifiers 2000-11
_[6] 서적 Physical Audio Signal Processing https://ccrma.stanfo[...] W3K Publishing 2020-03-28
_[7] 웹사이트 Beating Floating Point at its Own Game: Posit Arithmetic http://www.johngusta[...] 2019-12-28
_[8] 웹사이트 grex --- Growth-curve Explorer https://github.com/o[...] 2022-08-25
_[9] 서적 From Natural to Artificial Neural Computation
_[10] 문서 Software to fit an S-curve to a data set https://www.waterlog[...]
_[11] 저널 Variational Gaussian process classifiers