깎은 정사면체
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
깎은 정사면체는 정사면체의 각 꼭짓점을 잘라내어 얻는 다면체이다. 4개의 정삼각형과 4개의 정육각형으로 이루어져 있으며, 18개의 모서리와 12개의 꼭짓점을 갖는다. 모서리 길이가 a일 때, 겉넓이는 7√3a², 부피는 (23√2/12)a³이다. 깎은 정사면체는 정사면체와 동일한 대칭성을 가지며, 깎은 정사면체 그래프는 12개의 꼭짓점과 18개의 모서리를 가진 연결된 3차 그래프이다.
더 읽어볼만한 페이지
- 아르키메데스의 다면체 - 다듬은 정육면체
깎은 정육면체는 정육면체의 꼭짓점을 잘라 만든 다면체로, 6개의 정팔각형과 8개의 정삼각형으로 구성되고, 마름모 입방팔면체 등과 연관되며, 데카르트 좌표계와 트리보나치 수열로 꼭짓점 위치를 나타낼 수 있고, 키랄성 및 팔면체 대칭성을 가지며 여러 분야에 활용됩니다. - 아르키메데스의 다면체 - 깎은 정이십면체
깎은 정이십면체는 정이십면체의 꼭짓점을 잘라낸 아르키메데스의 다면체로, 32개의 면, 90개의 변, 60개의 꼭짓점을 가지며, 축구공, 풀러렌 분자 등 다양한 분야에서 활용된다. - 평면 그래프 - 다듬은 정육면체
깎은 정육면체는 정육면체의 꼭짓점을 잘라 만든 다면체로, 6개의 정팔각형과 8개의 정삼각형으로 구성되고, 마름모 입방팔면체 등과 연관되며, 데카르트 좌표계와 트리보나치 수열로 꼭짓점 위치를 나타낼 수 있고, 키랄성 및 팔면체 대칭성을 가지며 여러 분야에 활용됩니다. - 평면 그래프 - 정이십면체
정이십면체는 20개의 정삼각형 면으로 이루어진 볼록 정다면체로, 정반오각기둥 양쪽에 정오각뿔을 붙인 형태이며, 정십이면체와 쌍대 관계를 가지고 다양한 분야에서 활용된다.
| 깎은 정사면체 | |
|---|---|
| 개요 | |
| 종류 | 아르키메데스 다면체, 균일 다면체, 골드버그 다면체 |
| 면의 수 | 8 |
| 면의 종류 | 정육각형 4개, 정삼각형 4개 |
| 변의 수 | 18 |
| 꼭짓점의 수 | 12 |
| 쌍대 | 삼각뿔 사면체 |
| 대칭군 | 사면체 대칭 (Th) |
| 꼭짓점 도형 | 3.6.6 |
| 슐레플리 기호 | t{3, 3} |
| 위토프 기호 | 2 3 | 3 |
| 성질 | 볼록 다면체 |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
2. 구성
깎은 정사면체는 정사면체의 각 꼭짓점을 잘라내는 깎기 과정을 통해 만들 수 있다.[1] 깎은 정사면체는 4개의 정삼각형 면과 4개의 정육각형 면, 18개의 모서리, 12개의 꼭짓점을 갖는다.[2] 모서리 길이가 1일 때, 12개 꼭짓점의 데카르트 좌표는 다음과 같다.
한 모서리의 길이가 인 깎은 정사면체의 겉넓이 와 부피 는 다음과 같다.
증가 깎은 정사면체는 깎은 정사면체의 육각형 면에 삼각 돔을 붙여 만든 존슨의 다면체이다. 삼각깎은 정사면체는 깎은 정사면체의 삼각면에 세 개의 사면체를 더하여 구성한 다면체이다. 준정다면체로 분류되며, 삼각깎은 정사면체 벌집 구조와 같이 3차원 공간에서 테셀레이션될 수 있다.[1]
[1]
서적
An Atlas of Graphs
이는 마이너스 부호가 짝수 개인 점이다.
3. 성질
:
:
변의 길이가 인 경우, 깎은 정사면체의 표면적 는 4개의 정육각형과 4개의 정삼각형의 면적의 합이며, 부피 는 다음과 같다.
깎은 정사면체에서 삼각형과 육각형 사이의 이면각은 약 109.47°이며, 인접한 육각형 면 사이의 이면각은 약 70.53°이다. 깎은 정사면체의 가장 조밀한 쌓기는 로 추정된다. 깎은 정사면체에 대해 이것이 가능한 최상의 쌓기라는 수학적 증거는 없지만, 1에 가까운 값과 발견의 독립성으로 인해 훨씬 더 조밀한 쌓기가 발견될 가능성은 낮다.성질 값 외접구 반지름 중간접구 반지름 내접구 반지름 (삼각형) 내접구 반지름 (육각형) 겉넓이 부피 이면각 (3-6) 109.4712206° 이면각 (6-6) 70.52877936° 별 모양의 수 8 (표면만...4, 뒷면 사용...4)
4. 관련 다면체
J. B. 프리아우프의 이름을 따서 명명된 ''프리아우프 다면체''는 금속 원소 화합물로 형성된 금속간 화합물 구조로 설명된다.[2] 이는 마그네슘 아연 MgZn2와 같은 복합 금속 합금 결정에서 발견될 수 있다.[3] 프리아우프 다면체는 깎은 정사면체의 낮은 대칭 버전으로, 3차원 대칭군이 8차 이이각형군인 깎인 사각 이면체로 해석된다.
깎은 정사면체를 절단하면 54개의 모서리, 32개의 꼭짓점, 20개의 면(4개의 육각형, 4개의 구각형, 12개의 사다리꼴)이 생성된다. 이 다면체는 2010년 FIFA 월드컵을 위해 디자인된 자블라니 공의 기본 기하학으로 아디다스에서 사용되었다.[4]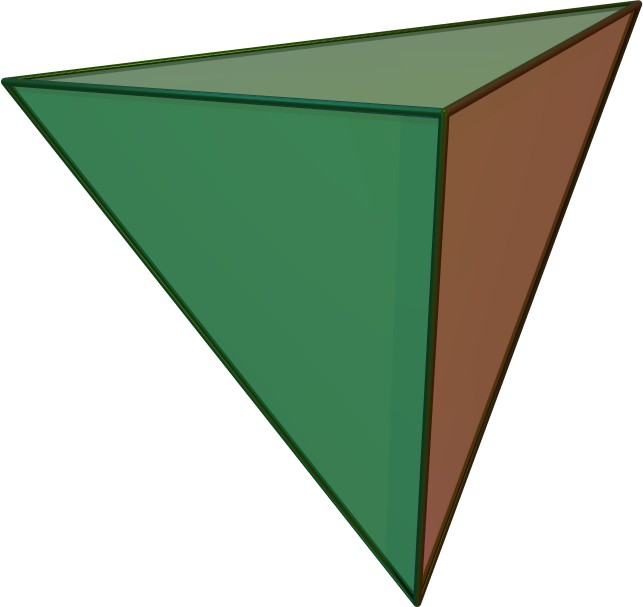
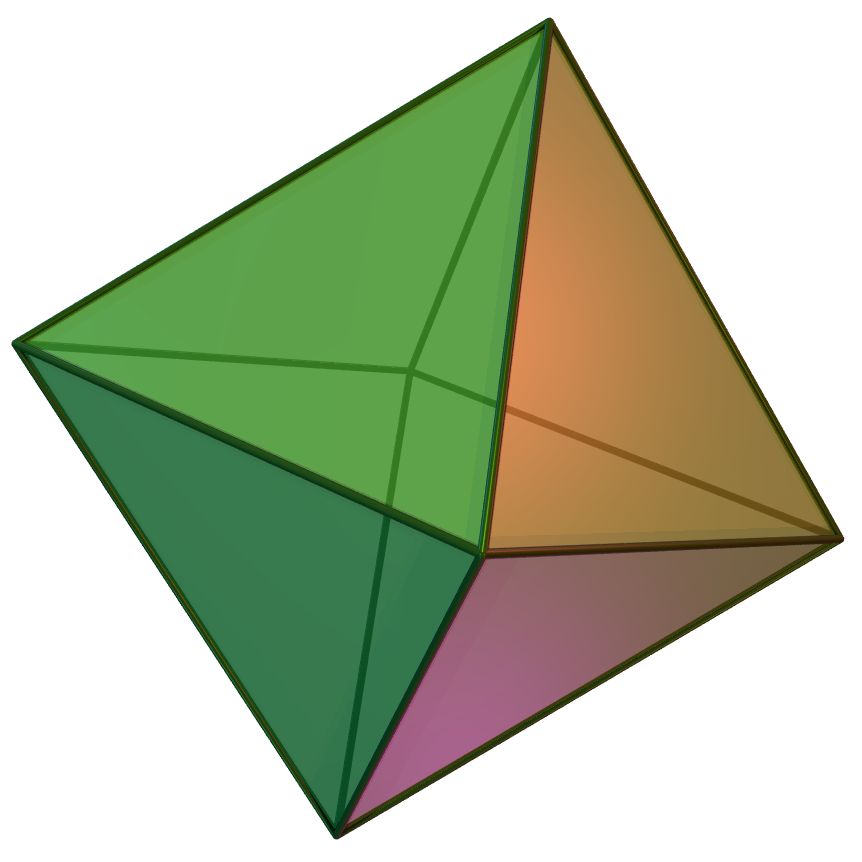
(절단면을 깊게)
5. 깎은 정사면체 그래프
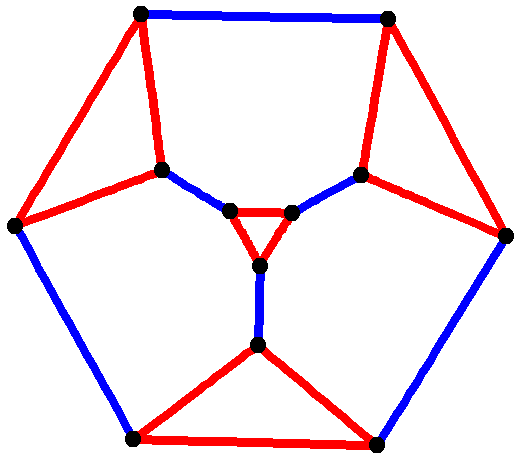
수학의 그래프 이론 분야에서, '''깎은 정사면체 그래프'''는 아르키메데스 그래프이며, 아르키메데스 다면체 중 하나인 깎은 정사면체의 꼭짓점과 모서리의 그래프이다. 이것은 12개의 꼭짓점과 18개의 모서리를 갖는다.[1] 이것은 연결된 3차 그래프이며,[2] 연결된 3차 추이 그래프이다.[3]
6. 예시
참조
[2]
서적
An Atlas of Graphs
[3]
서적
An Atlas of Graphs
[4]
논문
Regular-faced convex polyhedra
[5]
논문
Crystalline Assemblies and Densest Packings of a Family of Truncated Tetrahedra and the Role of Directional Entropic Forces
[6]
서적
Multi-shell Polyhedral Clusters
https://books.google[...]
Springer
[7]
논문
The crystal structure of the intermetallic compounds
[8]
논문
Tilings with congruent tiles
[9]
서적
Mathematical Physics: Proceedings of the 13th Regional Conference, Antalya, Turkey, 27–31 October 2010
World Scientific
[10]
논문
96.45 Can you 'bend' a truncated truncated tetrahedron?
[11]
arXiv
A Packing of Truncated Tetrahedra that Nearly Fills All of Space
[12]
논문
Convex polyhedra with regular faces
[13]
서적
Principles of Inorganic Materials Design
https://books.google[...]
John Wiley & Sons
[14]
서적
Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem
https://books.google[...]
Hindustan Book Agency
[15]
서적
The Geometrical Foundation of Natural Structure: A Source Book of Design
https://archive.org/[...]
Dover Publications, Inc.
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com