대기 확산 모델링

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

대기 확산 모델링은 대기 중 오염 물질의 이동과 확산을 예측하는 기술이다. 대기 확산 모델링은 대기층, 특히 행성 경계층(PBL) 내 오염 물질 확산을 이해하는 데 중요하다. 가우시안 방정식과 브릭스 플룸 상승 방정식은 대기 오염 물질 확산을 모델링하는 데 사용되는 주요 도구이다. 다양한 대기 확산 모델이 존재하며, ADMS, AERMOD, CALPUFF, HYSPLIT 등이 있다. 대기 질 모델링 그룹, 대기 자원 연구소 등 여러 기관이 대기 확산 모델링과 관련되어 있다.

더 읽어볼만한 페이지

대기 오염 - 질소 산화물
질소 산화물은 질소와 산소의 화합물로, 주로 일산화 질소와 이산화 질소를 지칭하며, 고온 연소 과정에서 발생하여 대기 환경 오염 및 인체에 유해한 영향을 미치고 아산화 질소는 오존층 파괴의 주범으로 알려져 질소 산화물 배출량 감축을 위한 기술이 활용되고 있다.
대기 오염 - 먼지
먼지는 0.001~1000μm 크기의 다양한 고체 입자로, 총먼지, 초미세먼지 등으로 나뉘며 무기, 유기, 혼합분진으로 분류되고, 발생원에 따라 건강과 환경에 다양한 영향을 미치며, 집먼지진드기, 우주 먼지 등도 포함된다.
환경공학 - 슬러리
슬러리는 액체에 고체 입자가 분산된 혼합물로, 농도에 따라 다양하게 존재하며 유동성을 이용해 성형하거나 특정 목적의 재료, 시멘트나 석탄 슬러리 등으로 산업 분야에서 활용되고, 계산을 통해 고체 비율, 액체 질량, 체적 분율 등을 파악한다.
환경공학 - 투수성 포장
투수성 포장은 빗물을 투과시켜 지하로 스며들게 하는 포장 방식으로, 물 튀김 방지, 열섬 현상 완화 등에 기여하지만, 시공 및 유지 관리 비용이 높고 내구성이 낮다는 특징을 갖는다.

대기 확산 모델링
개요
유형	대기 오염 모델
목적	대기 오염 물질의 확산 시뮬레이션
적용 분야	대기 질 관리 산업 안전 환경 영향 평가 재난 대응
모델 종류
가우시안 플룸 모델	단순한 모델로 계산 속도가 빠르다. 대기 안정도와 풍속이 일정하다는 가정하에 적용된다.
라그랑주 모델	입자 추적 모델이라고도 한다. 대기 중 입자의 움직임을 추적하여 확산을 계산한다.
오일러리안 모델	격자 기반 모델이라고도 한다. 공간을 격자로 나누고 각 격자에서의 농도 변화를 계산한다.
전산 유체 역학 (CFD) 모델	복잡한 지형이나 건물 주변의 확산을 시뮬레이션하는 데 사용된다. 높은 계산 비용이 필요하다.
입력 변수
배출원 정보	배출 위치 배출 높이 배출 유량 배출 온도 배출 속도 오염 물질의 종류
기상 조건	풍향 풍속 대기 안정도 기온 습도 강수량
지형 정보	지표면 높이 지표면 거칠기 건물 정보
모델 평가
측정 데이터 비교	모델 예측 결과와 실제 측정 데이터를 비교하여 모델의 정확도를 평가한다.
통계 지표 사용	평균 제곱근 오차 (RMSE) 상관 계수 (Correlation coefficient) 평균 절대 오차 (MAE)
모델링 소프트웨어
AERMOD	미국 환경 보호국 (EPA)에서 개발한 대기 확산 모델.
CALPUFF	장거리 확산 모델.
WRF-Chem	기상 모델과 화학 수송 모델을 결합한 모델.

2. 대기의 층

지구 대기는 대기 중 오염 물질이 어디로 확산되는지 이해하는 데 필요한 층들로 구성되어 있다. 지구 표면에서 위로 올라가면서, 행성 경계층(PBL), 자유 대류권, 성층권, 중간권 등으로 구성된다.

많은 대기 확산 모델은 주로 행성 경계층(PBL) 내의 대기 오염 물질 확산을 모델링하기 때문에 '경계층 모델'이라고 불린다. '중규모 모델'은 수평적으로 최대 수백 킬로미터까지 확장되는 확산 모델링 기능을 가지는데, 이는 중간권에서 확산을 모델링한다는 의미는 아니다.

2. 1. 대류권 (Troposphere)

지구 대기에 대한 이해는 대기 중 오염 물질이 어디로 확산되는지 파악하는 데 필수적이다. 지구 표면에 가장 가까운 층은 대류권으로, 해수면에서 약 18km 높이까지 뻗어 있으며 전체 대기의 질량의 약 80%를 포함한다. 대류권의 상부(즉, 기온 역전층 위)는 ''자유 대류권''이라고 불리며, 대류권계면(대류권과 성층권 사이의 경계)까지 뻗어 있다. 열대 및 중위도 지역의 주간에는 자유 대류층이 전체 대류권을 구성할 수 있으며, 이는 열대 수렴대에서 최대 10km에 달한다.^[1]

2. 2. 성층권 (Stratosphere)

지구 대기의 성층권은 대류권 상층부(약 18km)에서 약 50km까지 뻗어 있는 층이다. 지구 대기의 층은 대기 중 오염 물질이 확산되는 위치를 파악하는 데 중요한 역할을 한다.

2. 3. 중간권 (Mesosphere)

Mesosphere^영어은 지구 대기의 세 번째 층으로, 고도 50km에서 약 80km까지 뻗어 있다. 80 km 이상에는 다른 층이 있지만, 대기 확산 모델링과 관련하여 중요하지 않다.^[1]

2. 4. 행성 경계층 (Planetary Boundary Layer, PBL)

지구 대기의 층에 대한 이해는 대기 중 오염 물질이 어디로 확산되는지 파악하는 데 필수적이다. 지구 표면에 가장 가까운 층은 대류권으로, 해수면에서 약 18km 높이까지 뻗어 있으며 전체 대기의 질량의 약 80%를 포함한다. 성층권은 18km에서 약 50km까지, 중간권은 50km에서 약 80km까지 뻗어 있다. 80km 이상에도 다른 층이 있지만, 대기 확산 모델링에서는 중요하지 않다.

대류권의 가장 낮은 부분은 행성 경계층(PBL) 또는 대기 경계층이라고 불린다. PBL의 공기 온도는 고도가 높아짐에 따라 감소하다가 더 따뜻한 공기가 더 차가운 공기보다 대기 상층부에 위치하는 기온 역전층의 일종인 ''캡핑 역전''에 도달한다.

많은 대기 확산 모델은 주로 PBL 내의 대기 오염 물질 확산을 모델링하기 때문에 ''경계층 모델''이라고 불린다. ''중규모 모델''은 수평적으로 최대 수백 킬로미터까지 확장되는 확산 모델링 기능을 가지는데, 이는 중간권에서 확산을 모델링한다는 의미는 아니다.

2. 4. 1. 혼합층 (Mixing Layer)

지구 대기를 이해하는 것은 대기 중 오염 물질이 어디로 확산되는지 파악하는 데 중요하다. 지구 표면에 가장 가까운 층은 대류권이다. 대류권의 가장 낮은 부분은 행성 경계층(PBL) 또는 대기 경계층이라고 불린다. PBL의 공기 온도는 고도가 높아짐에 따라 감소하다가 기온 역전층의 일종인 ''캡핑 역전''에 도달한다. 캡핑 역전 아래의 PBL 영역을 대류성 행성 경계층이라고 하며, 일반적으로 높이가 1.5km에서 2km 사이이다.

PBL은 지구 표면에서 바람의 난류 역학이 가장 강하기 때문에 공기 중 오염 물질의 이동과 확산에서 중요하다. 지구 표면과 기온 역전층의 바닥 사이의 PBL 부분을 혼합층이라고 한다. 대기 중으로 방출되는 거의 모든 공기 중 오염 물질은 혼합층 내에서 이동하고 확산된다. 일부 배출물은 기온 역전층을 관통하여 PBL 위의 자유 대류권으로 들어간다.

2. 4. 2. 자유 대류권 (Free Troposphere)

대류권의 상부(즉, 기온 역전층 위)는 ''자유 대류권''이라고 불리며, 대류권계면(대류권과 성층권 사이의 지구 대기 경계)까지 뻗어 있다.^[1] 열대 및 중위도 지역의 주간에는 자유 대류층이 전체 대류권을 구성할 수 있으며, 이는 열대 수렴대에서 최대 10km에 달한다.^[1]

일부 오염 물질 배출은 PBL 위의 자유 대류권으로 기온 역전층을 관통하여 들어간다.^[1]

3. 가우시안 대기 오염 물질 확산 방정식

대기 오염 확산에 관한 연구는 1930년대부터 시작되었다. Bosanquet와 Pearson은 초기 대기 오염 물질 플룸 확산 방정식 중 하나를 유도했지만,^[2] 이 방정식은 정규 분포를 가정하지 않았고 오염 물질 플룸의 지면 반사 효과도 고려하지 않았다.

이후, 구형 모델은 안정성 등급(대기 오염 확산 용어 참조)에 기반하여 $\sigma_y$ 와 $\sigma_z$ 를 결정하는 반면, 최신 모델은 모닌-오부호프 유사성 이론을 사용하여 이러한 매개변수를 도출한다.

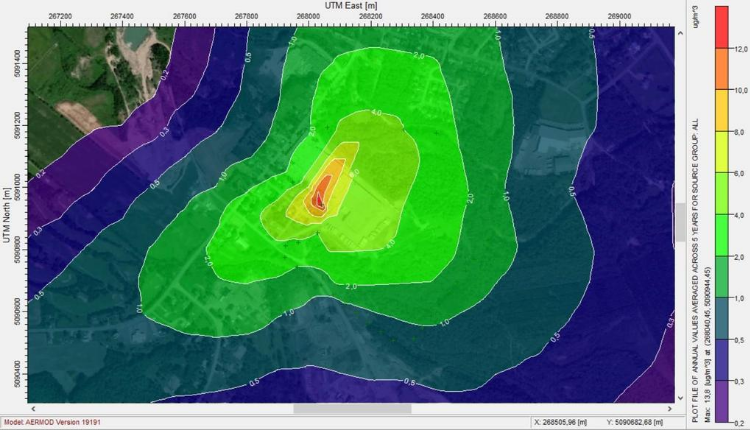
대기 오염 물질 농도 계산 결과는 공간적 변화를 가시화하기 위해 대기 오염 물질 농도 등고선으로 표현된다. 이 등고선은 민감한 수용체 위치와 겹쳐져 대기 오염 물질과 관심 지역 간의 공간적 관계를 나타낼 수 있다.

3. 1. 가우시안 방정식

1947년, Sir Graham Sutton은^[3] 플룸의 수직 및 횡풍 확산에 대한 정규 분포 가정을 포함하고 플룸의 지면 반사 효과도 포함하는 대기 오염 물질 플룸 확산 방정식을 유도했다.

엄격한 환경 규제의 출현으로 1960년대 후반부터 오늘날까지 대기 오염 물질 플룸 확산 계산 사용이 크게 증가했다. 이 기간 동안 개발된 대기 확산 모델의 대부분은 아래에 제시된 '''대기 오염 확산 용어에 대한 지속적이고 부유하는 대기 오염 플룸의 가우시안 확산 모델링을 위한 완전 방정식'''에 기반한다:^[4]^[5]

C = \frac{\;Q}{u}\cdot\frac{\;f}{\sigma_y\sqrt{2\pi}}\;\cdot\frac{\;g_1 + g_2 + g_3}{\sigma_z\sqrt{2\pi}}

여기서:
$f$	= 횡풍 확산 매개변수
	= $\exp\;[-\,y^2/\,(2\;\sigma_y^2\;)\;]$
$g$	= 수직 확산 매개변수 = $\,g_1 + g_2 + g_3$
$g_1$	= 반사 없음 수직 확산
	= $\; \exp\;[-\,(z - H)^2/\,(2\;\sigma_z^2\;)\;]$
$g_2$	= 지면 반사에 대한 수직 확산
	= $\;\exp\;[-\,(z + H)^2/\,(2\;\sigma_z^2\;)\;]$
$g_3$	= 상층 반전에 대한 수직 확산
	= $\sum_{m=1}^\infty\;\big\{\exp\;[-\,(z - H - 2mL)^2/\,(2\;\sigma_z^2\;)\;]$
	$+\, \exp\;[-\,(z + H + 2mL)^2/\,(2\;\sigma_z^2\;)\;]$
	$+\, \exp\;[-\,(z + H - 2mL)^2/\,(2\;\sigma_z^2\;)\;]$
	$+\, \exp\;[-\,(z - H + 2mL)^2/\,(2\;\sigma_z^2\;)\;]\big\}$
$C$	= 배출 농도(g/m³)로, 다음 위치에 있는 임의의 수용체에 대한 값이다.
	x (미터): 대기 오염 확산 용어에서 배출원 지점의 하향풍
	y (미터): 배출 플룸 중심선에서 횡풍
	z (미터): 지상 높이
$Q_{}$	= 오염 물질 배출율(g/s)
$u$	= 플룸 중심선을 따라 수평 풍속(m/s)
$H$	= 지상 높이 대비 배출 플룸 중심선의 높이(m)
$\sigma_z$	= 배출 분포의 수직 표준 편차(m)
$\sigma_y$	= 배출 분포의 수평 표준 편차(m)
$L_{}$	= 지상 높이에서 상층 반전 하단까지의 높이(m)
$\exp$	= 지수 함수

위의 방정식은 지면으로부터의 상향 반사뿐만 아니라 대기 중에 존재하는 반전 층 바닥으로부터의 하향 반사도 포함한다.

$g_3$ 에서 네 개의 지수 항의 합은 상당히 빠르게 최종 값으로 수렴한다. 대부분의 경우, ''m'' = 1, ''m'' = 2 및 ''m'' = 3으로 일련의 합계를 구하면 적절한 해를 제공한다.

$\sigma_z$ 와 $\sigma_y$ 는 대기 안정성 등급(즉, 주변 대기의 난류의 척도)과 수용체까지의 하향풍 거리에 대한 함수이다. 오염 물질 배출 확산 정도에 영향을 미치는 가장 중요한 두 변수는 배출원 지점의 높이와 대기 난류의 정도이다. 난류가 많을수록 확산 정도가 좋아진다.

$\sigma_y$ 와 $\sigma_z$ 에 대한 방정식은 다음과 같다.^[6]^[7]

$\sigma_y$ (x) = exp(I_y + J_yln(x) + K_y[ln(x)]²)

$\sigma_z$ (x) = exp(I_z + J_zln(x) + K_z[ln(x)]²)

( $\sigma_z$ 와 $\sigma_y$ 및 x의 단위는 미터)

계수	A	B	C	D	E	F
I_y	-1.104	-1.634	-2.054	-2.555	-2.754	-3.143
J_y	0.9878	1.0350	1.0231	1.0423	1.0106	1.0148
K_y	-0.0076	-0.0096	-0.0076	-0.0087	-0.0064	-0.0070
I_z	4.679	-1.999	-2.341	-3.186	-3.783	-4.490
J_z	-1.7172	0.8752	0.9477	1.1737	1.3010	1.4024
K_z	0.2770	0.0136	-0.0020	-0.0316	-0.0450	-0.0540

안정성 등급 분류는 F. Pasquill에 의해 제안되었다.^[8] 여섯 가지 안정성 등급은 다음과 같다.

A: 극도로 불안정
B: 중간 불안정
C: 약간 불안정
D: 중립
E: 약간 안정
F: 중간 안정

대기 오염 물질 농도에 대한 계산 결과는 연구 중인 넓은 지역에 걸쳐 오염 수준의 공간적 변화를 보여주기 위해 종종 대기 오염 물질 농도 등고선으로 표현된다. 이러한 방식으로 등고선은 민감한 수용체 위치에 오버레이될 수 있으며 대기 오염 물질과 관심 지역의 공간적 관계를 나타낸다.

구형 모델은

\sigma_y

와

\sigma_z

의 결정을 위해 안정성 등급(대기 오염 확산 용어 참조)에 의존하는 반면, 보다 최근 모델은 이러한 매개변수를 도출하기 위해 점점 더 모닌-오부호프 유사성 이론에 의존한다.

3. 2. 방정식의 변수

1947년 Sir Graham Sutton은^[3] 플룸의 수직 및 횡풍 확산에 대한 정규 분포 가정을 포함하고 플룸의 지면 반사 효과도 포함하는 대기 오염 물질 플룸 확산 방정식을 유도했다.

엄격한 환경 규제의 출현으로, 1960년대 후반부터 오늘날까지 대기 오염 물질 플룸 확산 계산 사용이 크게 증가했다. 이 기간 동안 대기 오염 물질 배출 확산을 계산하기 위한 수많은 컴퓨터 프로그램이 개발되었으며, 이를 "대기 확산 모델"이라고 불렀다. 이러한 모델의 대부분의 기반은 아래에 제시된 '''대기 오염 확산 용어에 대한 지속적이고 부유하는 대기 오염 플룸의 가우시안 확산 모델링을 위한 완전 방정식'''이었다:^[4]^[5]

C = \frac{\;Q}{u}\cdot\frac{\;f}{\sigma_y\sqrt{2\pi}}\;\cdot\frac{\;g_1 + g_2 + g_3}{\sigma_z\sqrt{2\pi}}

여기서:
$f$	= 횡풍 확산 매개변수
	= $\exp\;[-\,y^2/\,(2\;\sigma_y^2\;)\;]$
$g$	= 수직 확산 매개변수 = $\,g_1 + g_2 + g_3$
$g_1$	= 반사 없음 수직 확산
	= $\; \exp\;[-\,(z - H)^2/\,(2\;\sigma_z^2\;)\;]$
$g_2$	= 지면 반사에 대한 수직 확산
	= $\;\exp\;[-\,(z + H)^2/\,(2\;\sigma_z^2\;)\;]$
$g_3$	= 상층 반전에 대한 수직 확산
	= $\sum_{m=1}^\infty\;\big\{\exp\;[-\,(z - H - 2mL)^2/\,(2\;\sigma_z^2\;)\;]$
	$+\, \exp\;[-\,(z + H + 2mL)^2/\,(2\;\sigma_z^2\;)\;]$
	$+\, \exp\;[-\,(z + H - 2mL)^2/\,(2\;\sigma_z^2\;)\;]$
	$+\, \exp\;[-\,(z - H + 2mL)^2/\,(2\;\sigma_z^2\;)\;]\big\}$
$C$	= 배출 농도(g/m³)로, 다음 위치에 있는 임의의 수용체에서:
	x 미터, 대기 오염 확산 용어에서 배출원 지점의 하향풍
	y 미터, 배출 플룸 중심선에서 횡풍
	z 미터, 지상 높이
$Q_{}$	= 오염 물질 배출율(g/s)
$u$	= 플룸 중심선을 따라 수평 풍속(m/s)
$H$	= 지상 높이 대비 배출 플룸 중심선의 높이(m)
$\sigma_z$	= 배출 분포의 수직 표준 편차(m)
$\sigma_y$	= 배출 분포의 수평 표준 편차(m)
$L_{}$	= 지상 높이에서 상층 반전 하단까지의 높이(m)
$\exp$	= 지수 함수

위의 방정식은 지면으로부터의 상향 반사뿐만 아니라 대기 중에 존재하는 반전 층 바닥으로부터의 하향 반사도 포함한다.

$g_3$ 에서 네 개의 지수 항의 합은 상당히 빠르게 최종 값으로 수렴한다. 대부분의 경우, ''m'' = 1, ''m'' = 2 및 ''m'' = 3으로 일련의 합계를 구하면 적절한 해를 제공한다.

$\sigma_z$ 와 $\sigma_y$ 는 대기 안정성 등급(즉, 주변 대기의 난류의 척도)과 수용체까지의 하향풍 거리에 대한 함수이다. 오염 물질 배출 확산 정도에 영향을 미치는 가장 중요한 두 변수는 배출원 지점의 높이와 대기 난류의 정도이다. 난류가 많을수록 확산 정도가 좋아진다.

$\sigma_y$ 와 $\sigma_z$ 에 대한 방정식^[6]^[7]은 다음과 같다.

$\sigma_y(x)$ = exp(I_y + J_yln(x) + K_y[ln(x)]²)

$\sigma_z(x)$ = exp(I_z + J_zln(x) + K_z[ln(x)]²)

( $\sigma_z$ 와 $\sigma_y$ 및 x의 단위는 미터)

계수	A	B	C	D	E	F
I_y	-1.104	-1.634	-2.054	-2.555	-2.754	-3.143
J_y	0.9878	1.0350	1.0231	1.0423	1.0106	1.0148
K_y	-0.0076	-0.0096	-0.0076	-0.0087	-0.0064	-0.0070
I_z	4.679	-1.999	-2.341	-3.186	-3.783	-4.490
J_z	-1.7172	0.8752	0.9477	1.1737	1.3010	1.4024
K_z	0.2770	0.0136	-0.0020	-0.0316	-0.0450	-0.0540

안정성 등급 분류는 F. Pasquill에 의해 제안되었다.^[8] 여섯 가지 안정성 등급은 다음과 같다.

A: 극도로 불안정
B: 중간 불안정
C: 약간 불안정
D: 중립
E: 약간 안정
F: 중간 안정

4. 브릭스 플룸 상승 방정식

가우스 대기 오염 물질 확산 방정식은 오염 물질 플룸의 중심선 높이 ''H''를 입력값으로 필요로 한다. ''H''는 실제 배출원의 높이 ''H''_s와 플룸의 부력으로 인한 상승 높이 Δ''H''의 합이다.

1960년대 후반부터 2000년대 초반까지 개발된 대부분의 대기 확산 모델은 Δ''H''를 결정하기 위해 브릭스 방정식을 사용했다. 브릭스는 1965년에 플룸 상승 관찰 및 비교 결과를 처음 발표했다.^[9] 1968년에는 CONCAWE(네덜란드 기관) 후원 심포지엄에서 여러 플룸 상승 모델을 비교했고,^[10] 같은 해 슬레이드가 편집한 간행물에서 플룸 상승 모델 비교 분석 섹션을 작성했다.^[11] 1969년에는 플룸 상승 문헌에 대한 비판적 검토를 통해 "브릭스 방정식"으로 알려진 방정식을 제안했으며,^[12] 이후 1971년과 1972년에 수정했다.^[13]^[14]

4. 1. 플룸의 분류

G.A. 브릭스는 대기 오염 플룸을 다음과 같이 네 가지 범주로 나누었다.

잔잔한 주변 공기 조건에서의 차가운 제트 플룸
바람이 부는 주변 공기 조건에서의 차가운 제트 플룸
잔잔한 주변 공기 조건에서의 뜨겁고 부력 있는 플룸
바람이 부는 주변 공기 조건에서의 뜨겁고 부력 있는 플룸

브릭스는 차가운 제트 플룸의 궤적은 초기 속도 운동량에 의해 지배되며, 뜨겁고 부력 있는 플룸의 궤적은 부력 운동량에 의해 지배된다고 보았다. 브릭스가 제시한 플룸 상승 방정식 중에서 널리 사용되는 "브릭스 방정식"은 구부러진 뜨겁고 부력 있는 플룸에 대한 방정식이다.^[12]

일반적으로 구부러진 뜨겁고 부력 있는 플룸에 대한 브릭스 방정식은 대형 발전소에서 화석 연료를 연소하는 증기 발생 보일러의 굴뚝 가스 배출과 같은 전형적인 연소원에서 발생하는 플룸에 대한 관찰 및 데이터를 기반으로 한다. 이러한 굴뚝 배출 속도는 6m/s~30m/s 범위, 배출 온도는 120°C~260°C 범위였다.

브릭스 방정식에 사용되는 매개변수
매개변수	설명
Δh	플룸 상승 (단위: m)
F	부력 계수 (단위: m⁴s⁻³)
x	플룸 소스에서 하류 거리 (단위: m)
x_f	플룸 소스에서 최대 플룸 상승 지점까지의 하류 거리 (단위: m)
u	실제 굴뚝 높이에서의 풍속 (단위: m/s)
s	안정도 매개변수 (단위: s⁻²)

4. 2. 브릭스 방정식

가우스 대기 오염 물질 확산 방정식(위에서 논의됨)은 오염 물질 플룸의 지면 위 중심선 높이 ''H''를 필요로 한다. ''H''는 ''H''_s (오염 물질 플룸의 실제 배출원 지점의 물리적 높이)와 Δ''H'' (플룸의 부력으로 인한 플룸 상승)의 합이다.

Δ''H''를 결정하기 위해, 1960년대 후반과 2000년대 초반 사이에 개발된 대부분의 대기 확산 모델은 브릭스 방정식이라고 알려진 것을 사용했다. G.A. 브릭스는 1965년에 처음으로 플룸 상승 관찰 및 비교 결과를 발표했다.^[9] 1968년, CONCAWE(네덜란드 기관)가 후원한 심포지엄에서 그는 당시 문헌에서 이용 가능한 많은 플룸 상승 모델을 비교했다.^[10] 같은 해에 브릭스는 슬레이드가 편집한 간행물의 플룸 상승 모델 비교 분석에 관한 섹션도 작성했다.^[11] 그 후 1969년에는 전체 플룸 상승 문헌에 대한 그의 고전적인 비판적 검토가 이어졌으며, 여기에서 그는 "브릭스 방정식"으로 널리 알려지게 된 일련의 플룸 상승 방정식을 제안했다. 이후 브릭스는 1969년의 플룸 상승 방정식을 1971년과 1972년에 수정했다.^[13]^[14]

브릭스는 대기 오염 플룸을 다음과 같은 네 가지 일반적인 범주로 나누었다.

잔잔한 주변 공기 조건에서 차가운 제트 플룸
바람이 부는 주변 공기 조건에서 차가운 제트 플룸
잔잔한 주변 공기 조건에서 뜨겁고 부력 있는 플룸
바람이 부는 주변 공기 조건에서 뜨겁고 부력 있는 플룸

브릭스는 차가운 제트 플룸의 궤적은 초기 속도 운동량에 의해 지배되며, 뜨겁고 부력 있는 플룸의 궤적은 초기 속도 운동량이 상대적으로 중요하지 않을 정도로 부력 운동량에 의해 지배된다고 생각했다. 브릭스가 위 플룸 범주 각각에 대한 플룸 상승 방정식을 제안했지만, 널리 사용되는 "브릭스 방정식"은 그가 구부러진 뜨겁고 부력 있는 플룸에 대해 제안한 방정식이라는 점을 강조하는 것이 중요하다.

일반적으로, 구부러진 뜨겁고 부력 있는 플룸에 대한 브릭스의 방정식은 대형 발전소에서 화석 연료를 태우는 증기 발생 보일러의 굴뚝 가스 굴뚝과 같은 전형적인 연소원에서 발생하는 플룸에 대한 관찰 및 데이터를 기반으로 한다. 따라서 굴뚝 배출 속도는 20ft/s~100ft/s 범위에 있었고 배출 온도는 약 121.1°C~약 260.0°C 범위에 있었다.

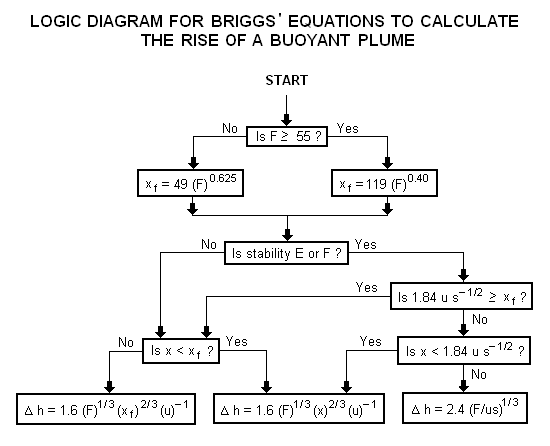
구부러진 부력 플룸의 플룸 상승 궤적을 얻기 위해 브릭스 방정식^[4]을 사용하는 논리 다이어그램은 다음과 같다.

where:
Δh	= 플룸 상승, m 단위
F	= 부력 계수, m⁴s⁻³ 단위
x	= 플룸 소스에서 하류 거리, m 단위
x_f	= 플룸 소스에서 최대 플룸 상승 지점까지의 하류 거리, m 단위
u	= 실제 굴뚝 높이에서의 풍속, m/s 단위
s	= 안정도 매개변수, s⁻² 단위

브릭스 방정식에 사용된 위 매개변수는 베이촉의 책^[4]에서 논의되었다.

5. 대기 확산 모델의 종류

대기 확산 모델 목록에서 더 광범위한 모델 목록과 각 모델에 대한 간략한 설명을 확인할 수 있다.

5. 1. 주요 모델 목록

ADMS
AERMOD

ATSTEP
CALPUFF
CMAQ
DISPERSION21
FLACS
FLEXPART

HYSPLIT
ISC3
NAME
MERCURE
OSPM
Fluidyn-Panache
RIMPUFF
SAFE AIR
PUFF-PLUME
[http://cerea.enpc.fr/polyphemus/ POLYPHEMUS]
[http://cerea.enpc.fr/munich/ MUNICH]

6. 관련 기관 및 기타 정보

이 섹션에서는 대기 확산 모델링과 관련된 기관 및 기타 정보들을 확인할 수 있다.

'''관련 기관:'''

대기 질 모델링 그룹
대기 자원 연구소
핀란드 기상 연구소
KNMI, 왕립 네덜란드 기상 연구소
덴마크 국립 환경 연구소
스웨덴 기상 수문 연구소
TA Luft
영국 대기 확산 모델링 연락 위원회
영국 확산 모델링 국
사막 연구소
VITO(벨기에)
스웨덴 국방 연구 기관(FOI)

'''기타:'''

대기 오염 확산 용어
대기 확산 모델 목록
이동 배출 측정 시스템(PEMS)
도로 대기 확산 모델링
대기 확산 모델링에 유용한 변환 및 공식
대기 오염 예측

6. 1. 관련 기관

대기 질 모델링 그룹
대기 자원 연구소
핀란드 기상 연구소
KNMI, 왕립 네덜란드 기상 연구소
덴마크 국립 환경 연구소
스웨덴 기상 수문 연구소
TA Luft
영국 대기 확산 모델링 연락 위원회
영국 확산 모델링 국
사막 연구소
VITO(벨기에)
스웨덴 국방 연구 기관(FOI)

6. 2. 기타

대기 오염 확산 용어
대기 확산 모델 목록
이동 배출 측정 시스템(PEMS)
도로 대기 확산 모델링
대기 확산 모델링에 유용한 변환 및 공식
대기 오염 예측

참조

_[1] 논문 Reduction of air pollution potential through environmental planning https://www.tandfonl[...]
_[2] 논문 The spread of smoke and gases from chimneys
_[3] 논문 The problem of diffusion in the lower atmosphere
_[4] 서적 Fundamentals Of Stack Gas Dispersion author-published
_[5] 서적 Workbook of atmospheric dispersion estimates: an introduction to dispersion modeling https://archive.org/[...] CRC Press
_[6] 서적 Atmospheric chemistry and physics: from air pollution to climate change Wiley
_[7] 보고서 Handbook on Atmospheric Diffusion https://www.osti.gov[...] U.S. Department of Energy Report
_[8] 서적 Atmospheric Diffusion (3rd Edition). F. Pasquill and F. B. Smith. Ellis Horwood, (John Wiley & Sons) Chichester, 1983 Quarterly Journal of the Royal Meteorological Society 1984-04-00
_[9] 논문 A plume rise model compared with observations
_[10] 논문 CONCAWE meeting: discussion of the comparative consequences of different plume rise formulas
_[11] 보고서 Meteorology and atomic energy 1968 Air Resources Laboratory, U.S. Dept. of Commerce
_[12] 보고서 Plume Rise USAEC Critical Review Series
_[13] 논문 Some recent analyses of plume rise observation Proc. Second Internat'l. Clean Air Congress, Academic Press, New York
_[14] 논문 Discussion: chimney plumes in neutral and stable surroundings
_[15] 서적 二訂･大気汚染対策の基礎知識丸善

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com