정규 분포
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
정규 분포는 평균과 분산으로 정의되는 확률 분포로, 통계학에서 가장 널리 사용되는 분포 중 하나이다. 1733년 아브라암 드무아브르에 의해 처음 소개되었으며, 피에르시몽 라플라스, 카를 프리드리히 가우스 등에 의해 연구되었다. 정규 분포는 종 모양의 대칭적인 곡선 형태를 가지며, 중심 극한 정리에 따라 독립적인 확률 변수의 합이 정규 분포에 가까워지는 특성을 보인다. 다양한 분야에서 응용되며, 특히 자연 현상, 측정 오차, 금융 시장 분석 등에 활용된다. 표준 정규 분포, 다변량 정규 분포 등 여러 변형이 존재하며, 가설 검정, 신뢰 구간 설정, 모수 추정 등 통계적 추론에 널리 사용된다.
아브라암 드무아브르는 1733년에 쓴 글에서 특정 이항 분포의 이 클 때 그 분포의 근사치를 계산하는 것과 관련하여 정규분포를 처음 소개하였고, 이 글은 그의 저서 《우연의 교의》(The Doctrine of Chances) 2판(1738년)에 다시 실렸다.[90] 피에르시몽 라플라스는 그의 저서 《확률론의 해석이론》(Théorie analytique des probabilités)(1812년)에서 이 결과를 확장하였고 이는 오늘날 드무아브르-라플라스 정리로 알려져있다.
정규 분포는 확률 밀도 함수가 다음과 같은 형태(가우스 함수라고 불림)로 주어지는 확률 분포이다.[84]
정규분포에서는 기댓값, 최빈값, 중앙값이 모두 로 같다. 정규분포의 기댓값은 특정 수식으로 계산할 수 있는데, 이 과정에서 첫 번째 적분은 홀함수의 적분으로 0이 되고, 두 번째 적분은 가우스 적분으로 적분값이 로 알려져 있어, 결국 기댓값은 가 된다.
2. 역사
라플라스는 실험 오차를 분석하면서 정규분포를 사용했다.[72] 1805년에는 아드리앵마리 르장드르가 최소제곱법을 도입했고, 카를 프리드리히 가우스는 1794년부터 이 방법을 사용해왔다고 주장했는데 1809년에는 실험 오차가 정규분포를 따른다는 가정하에 최소제곱법을 이론적으로 엄밀히 정당화했다.
일부 저자들은 1738년에 드 무아브르에게 정규 분포의 발견을 돌린다.[66][67] 그는 이항 전개에서 1733년에 팸플릿으로 처음 발표하고, 1738년에 공개적으로 발표한 확률의 원리의 두 번째 판에 해당 내용을 게시했다. 드 무아브르는 이 전개의 중간 항이 대략 의 크기를 가지며, "만약 ''m'' 또는 ''n''이 무한히 큰 양이라면, 중간 항으로부터 ''ℓ''만큼 떨어진 항이 중간 항에 대한 비율의 로그는 이다."라는 것을 증명했다.[68] 비록 이 정리가 정규 확률 법칙의 첫 번째 모호한 표현으로 해석될 수 있지만, 스티글러는 드 무아브르 자신은 자신의 결과를 이항 계수의 근사 규칙 이상으로 해석하지 않았으며, 특히 드 무아브르는 확률 밀도 함수에 대한 개념이 없었다고 지적한다.[69]
1823년 가우스는 그의 논문에서 최소제곱법, 최대 우도법, 그리고 ''정규 분포''와 같은 몇 가지 중요한 통계적 개념을 소개했다. 가우스는 어떤 알려지지 않은 양 ''V''의 측정을 나타내기 위해 ''M'', ''M''′, ''M''′′ 등을 사용했으며, 관찰된 실험 결과를 얻을 확률을 최대화하는 가장 가능성이 높은 추정치를 찾았다. 그의 표기법에서 φΔ는 Δ 크기의 측정 오차의 확률 밀도 함수이다. 함수 ''φ''가 무엇인지 알 수 없었기 때문에 가우스는 그의 방법이 잘 알려진 답, 즉 측정값의 산술 평균으로 축소되도록 요구했다.[70] 가우스는 이러한 원리에서 시작하여 위치 매개변수의 추정치로 산술 평균의 선택을 합리화하는 유일한 법칙은 오차의 정규 법칙임을 증명한다.
:
여기서 ''h''는 "관측의 정밀도 척도"이다. 가우스는 이러한 정규 법칙을 실험에서 오차에 대한 일반적인 모델로 사용하여 현재 비선형 최소제곱법 가중 최소제곱법으로 알려진 방법을 공식화했다.[71]
가우스가 정규 분포 법칙을 처음 제안했지만, 라플라스는 중요한 기여를 했다.[72] 라플라스는 1774년에 여러 관측값을 집계하는 문제를 처음 제기했지만, 그의 해결책은 라플라스 분포로 이어졌다. 라플라스는 1782년에 적분의 값을 처음 계산하여 정규 분포에 대한 정규화 상수를 제공했다.[73] 이 업적에 대해 가우스는 라플라스의 우선권을 인정했다.[74] 마지막으로, 1810년 라플라스는 정규 분포의 이론적 중요성을 강조하는 근본적인 중심 극한 정리를 증명하여 학회에 제시했다.[75]
1809년에 아일랜드계 미국인 수학자 로버트 에이드리언이 가우스와 동시에 독립적으로 정규 확률 법칙에 대한 통찰력 있지만 결함이 있는 두 가지 유도를 발표했다는 점은 주목할 만하다.[76] 그의 작품은 1871년 애비에 의해 발굴될 때까지 과학계에서 거의 주목받지 못했다.[77]
19세기 중반에 맥스웰은 정규 분포가 단순히 편리한 수학적 도구일 뿐만 아니라 자연 현상에서도 발생할 수 있음을 증명했다.[78] 특정 방향으로 분해된 속도가 ''x''와 ''x'' + ''dx'' 사이에 있는 입자의 수는 다음과 같다.
:
오늘날 이 개념은 영어로 일반적으로 '''정규 분포''' 또는 '''가우스 분포'''로 알려져 있다.
"벨 커브"라는 이름은 1872년에 2변수 정규 분포에 대해 "종 모양 곡면"이라는 말을 사용한 에 거슬러 올라간다. "정규 분포"라는 말은 찰스 샌더스 퍼스, 프랜시스 골턴, 빌헬름 렉시스의 3인에 의해 1875년경에 독립적으로 도입되었다.
가우스는 응용 분야와 관련된 "정규 방정식"과 관련하여 이 용어를 만든 것으로 보이며, 여기서 정규는 일반적인 의미가 아닌 직교의 기술적인 의미를 갖는다.[79] 그러나 19세기 말에는 일부 저자들이 "정규 분포"라는 이름을 사용하기 시작했는데, 여기서 "정규"라는 단어는 형용사로 사용되었고, 이 분포가 전형적이고 일반적인 것으로 간주되어 정규적임을 반영하는 것으로 여겨졌다. 퍼스는 한때 "정규"를 다음과 같이 정의했다. "... '정규'는 실제로 발생하는 것의 평균(또는 다른 종류의 평균)이 아니라, 장기적으로 어떤 상황에서 '발생할' 것의 평균이다."[80] 20세기 초 칼 피어슨은 이 분포를 지칭하는 용어로 ''정규''를 대중화했다.[81]
또한, 현대 표기법에서 표준 편차 ''σ''를 사용하여 분포를 처음으로 쓴 사람도 피어슨이었다. 이 직후 1915년, 로널드 피셔는 정규 분포 공식에 위치 매개변수를 추가하여 오늘날과 같은 방식으로 표현했다.
:
평균이 0이고 분산이 1인 정규 분포를 나타내는 "표준 정규"라는 용어는 1950년대에 일반화되었으며, P. G. Hoel (1947)의 ''수리 통계학 입문''과 A. M. Mood (1950)의 ''통계 이론 입문''과 같은 대중적인 교과서에 등장했다.[82]
3. 정의
:
이 분포는 로 표기한다.[84] 여기서 N는 "정규 분포"를 나타내는 영어 "normal distribution"의 머리글자에서 따온 것이다.[84]
확률 변수 가 평균 와 표준 편차 를 갖는 정규 분포를 따르면 다음과 같이 쓸 수 있다.
평균이 , 분산이 인 정규 분포는 지수족을 형성하며, 자연 매개변수는 및 이고 자연 통계량은 ''x'' 및 ''x''2이다. 정규 분포에 대한 이중 기대 매개변수는 및 이다.
일부에서는 분포의 폭을 정의하는 매개변수로 표준 편차 또는 분산 대신 정밀도 를 사용할 것을 주장한다. 정밀도는 일반적으로 분산의 역수 로 정의된다.[10] 이 경우 분포에 대한 공식은 다음과 같다.
또는 표준 편차의 역수 를 "정밀도"로 정의할 수 있으며, 이 경우 정규 분포의 표현식은 다음과 같다.
3. 1. 일반 정규 분포
모든 정규 분포는 표준 정규 분포의 변형으로, 정의역이 σ (표준 편차)만큼 팽창되고 μ (평균)만큼 평행 이동된 것이다.
만약 Z가 표준 정규 편차라면, X = σZ + μ는 기대값 μ와 표준 편차 σ를 갖는 정규 분포를 갖게 된다. 이는 표준 정규 분포 Z가 σ만큼 척도/팽창되고 μ만큼 이동되어 X라고 불리는 다른 정규 분포를 생성할 수 있다는 것과 같다. 반대로, X가 매개변수 μ와 σ²를 갖는 정규 편차라면, 이 X 분포는 공식 Z = (X - μ) / σ를 통해 재조정 및 이동하여 표준 정규 분포로 변환할 수 있다. 이 변량은 X의 표준화된 형태라고도 불린다.[84]
평균을 μ, 분산을 σ² > 0으로 하는 (1차원) 정규 분포는 확률 밀도 함수가 다음과 같은 형태 (가우스 함수라고 불림)
:
로 주어지는 확률 분포를 말한다.[84] 이 분포를 N(μ, σ²)로 표기한다.[84] (N는 "정규 분포"를 나타내는 영어 "normal distribution"의 머리글자에서 따온 것이다)[84]
3. 2. 표준 정규 분포
정규 분포 밀도 함수에서 를 통해 X(원점수)를 Z(Z점수)로 정규화함으로써 평균이 0, 표준편차가 1인 표준 정규 분포를 얻을 수 있다.[84]
z-분포라고도 부르며, z-분포로 하는 검정(test)을 z검정(z-test)이라고 한다. '''표준 정규 분포''' 또는 '''단위 정규 분포'''는 정규 분포의 가장 간단한 경우로, 이고 일 때의 특수한 경우이며, 다음 확률 밀도 함수로 설명된다.
변수 는 평균이 0이고 분산과 표준 편차가 1이다. 밀도 는 에서 최고점 를 가지며 과 에서 변곡점을 가진다.
표준 가우스 분포(표준 정규 분포, 평균 0, 분산 1)의 확률 밀도는 종종 그리스 문자 (Φ)로 표기한다.[8] 그리스 문자 Φ의 다른 형태인 도 자주 사용된다.
정규 분포는 또는 로 표기한다.[9] 따라서 확률 변수 가 평균 와 표준 편차 를 갖는 정규 분포를 따르면 다음과 같이 쓸 수 있다.
특히 , 일 때, 이 분포는 (1차원) '''표준 정규 분포''' (또는 기준정규분포)라고 불린다. 즉, 표준 정규 분포 는
가 되는 확률 밀도 함수를 갖는 확률 분포이다.[84]
4. 성질
정규분포는 절대근사하며, 평균과 표준편차가 주어졌을 때 엔트로피를 최대화하는 분포이다. 정규분포곡선은 좌우 대칭이며 하나의 꼭지를 가지고, 중앙값에 사례 수가 모여있고 양극단으로 갈수록 X축에 무한히 접근하지만 X축에 닿지는 않는다.[91]
에서 k값에 따라 구해지는 값을 '''불확실성'''(uncertainty)이라고 한다. 예를 들어, 는 95% 불확실성을 의미한다. 는 50% 불확실성이며, '''확률오차'''(probable error)라고도 하는데, 이는 관측값이 전체 관측값의 50%에 있을 확률을 의미한다.[92]
오차 함수 는 평균 0, 분산 1/2의 정규 분포를 갖는 임의 변수가 범위에 속할 확률을 나타낸다. 이 적분은 초등 함수로 표현될 수 없으며, 특수 함수라고도 한다. 그러나 많은 수치 근사값이 알려져 있다. 두 함수는 서로 밀접하게 관련되어 있으며, 누적 분포 함수는 다음과 같이 표현된다.
표준 정규 누적 분포 함수의 여집합 는 Q-함수라고 불리며[11][12], 표준 정규 임의 변수 의 값이 를 초과할 확률 를 제공한다.[13]
표준 정규 누적 분포 함수 의 그래프는 점 (0,1/2)에 대해 2배의 회전 대칭을 가지며, 그 부정 적분은 특정 형태로 표현될 수 있다. 또한, 부분 적분법을 사용하여 급수로 전개될 수 있으며, 큰 ''x''에 대한 누적 분포 함수의 점근 전개 역시 부분 적분법을 사용하여 유도될 수 있다.[14]
정규 분포에서 추출된 값의 약 68%는 평균에서 표준 편차 ''σ'' 1개 이내, 약 95%는 2 표준 편차 이내, 약 99.7%는 3 표준 편차 이내에 있다.[6] 이를 68–95–99.7 (경험적) 규칙 또는 ''3-시그마 규칙''이라고 한다.
정규 편차가 와 사이의 범위에 속할 확률은 특정 수식으로 계산되며, 일 때 12자리 유효 숫자로 나타낸 값은 다음 표와 같다.OEIS 1 0.682689492137 0.317310507863 3.15148718753 A178647 2 0.954499736104 0.045500263896 21.9778945080 A110894 3 0.997300203937 0.002699796063 370.398347345 A270712 4 0.999936657516 0.000063342484 15787.1927673 5 0.999999426697 0.000000573303 1744277.89362 6 0.999999998027 0.000000001973 506797345.897
큰 의 경우, 근사식을 사용할 수 있다. 정규 분포는 처음 두 개(즉, 평균과 분산)를 제외한 큐뮬런트가 0인 유일한 분포이며, 주어진 평균과 분산에 대해 최대 엔트로피 확률 분포를 갖는 연속 분포이기도 하다.[16][17] 정규 분포는 평균과 분산이 서로 독립적인 유일한 분포이다.[18][19]
정규 분포는 타원 분포의 하위 클래스이며, 평균에 대해 대칭 분포이고, 전체 실수선에서 0이 아닌 값을 갖는다. 따라서 양수이거나 심하게 왜곡된 변수에는 적합한 모델이 아닐 수 있으며, 이러한 변수는 로그 정규 분포 또는 파레토 분포와 같은 다른 분포로 더 잘 설명될 수 있다.
정규 밀도의 값은 값 가 평균에서 여러 표준 편차 이상 떨어져 있을 때 거의 0에 가깝다. 따라서 상당한 비율의 이상치가 예상될 경우 적절한 모델이 아닐 수 있으며, 이러한 경우 더 헤비 테일 분포를 가정하고 적절한 강건 통계적 추론 방법을 적용해야 한다.
가우스 분포는 안정 분포의 한 종류에 속하며, 독립 동일 분포의 합의 흡인자이다. 가우스를 제외한 모든 안정 분포는 헤비 테일과 무한 분산을 갖는다. 이는 안정적이고 확률 밀도 함수가 해석적으로 표현될 수 있는 몇 안 되는 분포 중 하나이며, 나머지 분포는 코시 분포와 레비 분포이다.
실수 확률 변수 의 적률생성함수는 실수 매개변수 의 함수로서 의 기댓값이다. 정규 분포의 경우, 적률생성함수는 존재하며 특정 형태로 주어진다. 누적률생성함수는 적률생성함수의 로그이며, 2차 다항식으로 처음 두 개의 누적률만 0이 아니며, 평균과 분산이다.
일부 저자는 특성함수를 사용하는 것을 선호한다. 이 0으로 접근하는 극한에서, 확률 밀도 는 특정 지점에서 0으로 접근하지만, 다른 지점에서는 한없이 커진다. 하지만 적분값은 1로 유지된다. 따라서, 정규 분포는 일 때 일반적인 함수로 정의될 수 없다. 하지만, 분산이 0인 정규 분포는 일반화 함수로 정의할 수 있으며, 특히 디랙 델타 함수를 평균만큼 평행이동한 것으로 정의할 수 있다. 이 경우 누적 분포 함수는 평균만큼 평행이동된 헤비사이드 계단 함수가 된다.
정규 분포의 추가적인 성질은 다음과 같다.
# 어떤 확률 변수의 특성 함수가 특정 형태를 띠면, '''마르친키에비츠 정리'''에 따르면 그 확률 변수는 정규 확률 변수이다.[46]
# 결합 정규 분포이고 상관관계가 없는 경우 두 확률 변수는 독립이다.[31][32][증명
# 두 정규 분포 간의 쿨백-라이블러 발산과 헬린저 거리는 특정 수식으로 주어진다.[33]
# 정규 분포의 피셔 정보 행렬은 대각 행렬이며 특정 형태를 취한다.[34]
# 정규 분포 평균의 켤레 사전 분포는 또 다른 정규 분포이다.[34]
# 정규 분포군은 지수족을 형성하며, 자연 지수족을 형성한다.
# 정규 분포군은 상수 곡률을 갖는 통계적 다양체를 형성한다.[35]
# 독립적인 확률 변수들의 최댓값은 특정 값 이하이다.[36]
임의의 양의 정수에 대해, 평균과 분산을 갖는 모든 정규 분포는 독립적인 정규 확률 변수의 합의 분포이다. 이 성질을 무한 분할 가능성이라고 한다.[44]
반대로, 독립적인 확률 변수의 합이 정규 분포를 갖는다면, 각 확률 변수 모두 정규 확률 변수여야 한다.[45] 이 결과는 크라메르 분해 정리로 알려져 있다. 크라메르 정리는 독립적인 비-가우시안 변수의 선형 결합은 결코 정확히 정규 분포를 가질 수 없음을 의미한다.[46]
카츠-번스타인 정리는 독립적인 두 확률 변수의 합과 차가 독립적이면, 두 확률 변수 모두 반드시 정규 분포를 가져야 한다고 명시한다.[47][48]
더 일반적으로, 독립적인 확률 변수들의 두 선형 결합이 독립적이기 위한 조건이 특정 형태로 주어진다.[47]
정규 분포는 재생성을 갖는다. 즉, 독립적인 정규 분포를 따르는 확률 변수들의 선형 결합 또한 정규 분포를 따른다.
300px
정규 분포에서 무작위 표본을 추출할 때, 평균에서 벗어나는 정도에 따라 표본이 포함될 확률이 결정된다.[84] 정규 분포는 t-분포나 F-분포와 같은 여러 분포의 기본이 되며, 통계적 추론에서 다양하게 활용된다. 정규 분포를 따르는 확률 변수를 표준화하면 표준 정규 분포를 따르게 되며, 이를 통해 표준 정규 분포표를 이용하여 확률을 구할 수 있다. 불연속 값을 갖는 확률 변수에 대한 검정의 경우에도 정규 분포를 근사적으로 사용할 수 있다.신뢰 구간 신뢰도 위험률 백분율 백분율 비율 0.318639σ 25% 75% 3/4 0.674490σ 50% 50% 1/2 0.994458σ 68% 32% 1/3.125 1σ 68.2689492% 31.7310508% 1/3.1514872 1.281552σ 80% 20% 1/5 1.644854σ 90% 10% 1/10 1.959964σ 95% 5% 1/20 2σ 95.4499736% 4.5500264% 1/21.977895 2.575829σ 99% 1% 1/100 3σ 99.7300204% 0.2699796% 1/370.398 3.290527σ 99.9% 0.1% 1/1000 3.890592σ 99.99% 0.01% 1/10000 4σ 99.993666% 0.006334% 1/15787 4.417173σ 99.999% 0.001% 1/100,000 4.5σ 99.9993204653751% 0.0006795346249% 1/14,7159.5358 4.891638σ 99.9999% 0.0001% 1/1,000,000 5σ 99.9999426697% 0.0000573303% 1/1,744,278 5.326724σ 99.99999% 0.00001% 1/10,000,000 5.730729σ 99.999999% 0.000001% 1/100,000,000 6σ 99.9999998027% 0.0000001973% 1/5,0679,7346 6.109410σ 99.9999999% 0.0000001% 1/100,000,000 6.466951σ 99.99999999% 0.00000001% 1/1,000,000,000 6.806502σ 99.999999999% 0.000000001% 1/10,000,000,000 7σ 99.9999999997440% 0.000000000256% 1/3906,8221,5445
4. 1. 누적 분포 함수
표준 정규 분포의 누적 분포 함수(CDF)는 대문자 그리스 문자 로 표시되며, 다음과 같은 적분으로 나타낼 수 있다.
의 도함수 군(群)의 재귀적 특성은 분포의 알려진 값 의 임의의 점에 대해 재귀적 항목을 사용하여 빠르게 수렴하는 테일러 급수 전개를 쉽게 구성하는 데 사용될 수 있다.
여기서:
위의 테일러 급수 전개의 응용은 뉴턴 방법을 사용하여 계산을 역으로 수행하는 것이다. 즉, 누적 분포 함수 의 값을 알고 있지만, 해당 를 얻기 위해 필요한 x 값을 모르는 경우, 뉴턴 방법을 사용하여 x를 찾을 수 있으며, 위에서 언급한 테일러 급수 전개를 사용하여 계산 횟수를 최소화할 수 있다. 뉴턴 방법은 이 문제를 해결하는 데 이상적인데, 그 이유는 의 1차 도함수, 즉 표준 정규 분포의 적분은 표준 정규 분포이며, 뉴턴 방법 해에서 쉽게 사용할 수 있기 때문이다.
해결하려면 원하는 에 대한 알려진 근사해 를 선택한다. 은 분포표의 값일 수도 있고, 원하는 계산 방법을 사용하여 를 계산한 지능적인 추정치일 수도 있다. 이 값과 위의 테일러 급수 전개를 사용하여 계산을 최소화한다.
계산된 과 원하는 (이를 라고 부릅니다)의 차이가 10−5, 10−15 등과 같이 허용 가능한 작은 오차보다 작아질 때까지 다음 과정을 반복한다.
여기서
: 은 과 를 사용하여 테일러 급수 해에서 얻은 이다.
반복적인 계산이 선택된 허용 가능한 작은 값보다 작은 오차로 수렴되면, ''x''는 원하는 값 의 를 얻기 위해 필요한 값이 된다.
표준 정규 누적 분포 함수는 과학 및 통계 계산에서 널리 사용된다.
Φ(''x'') 값은 수치 적분, 테일러 급수, 점근 급수 및 연분수와 같은 다양한 방법을 통해 매우 정확하게 근사될 수 있다. 원하는 정확도 수준에 따라 다른 근사가 사용된다.
여기서 ''ϕ''(''x'')는 표준 정규 확률 밀도 함수이고, ''b''0 = 0.2316419, ''b''1 = 0.319381530, ''b''2 = −0.356563782, ''b''3 = 1.781477937, ''b''4 = −1.821255978, ''b''5 = 1.330274429이다.
를 기반으로 임의의 정밀도로 를 계산하는 간단한 알고리즘을 제안했다. 이 알고리즘의 단점은 계산 시간이 비교적 느리다는 것이다(예를 들어, 일 때 16자리 정밀도로 함수를 계산하는 데 300번 이상 반복해야 한다).
\left(\approx 1.1 \times 10^{-16}\right)
보다 작다.
에 대해
이고 에 대해,
Shore (1982)는 신뢰성 공학 및 재고 분석과 같은 공학 및 운영 연구의 확률적 최적화 모델에 통합될 수 있는 간단한 근사를 도입했다. 로 표시하면, 분위 함수에 대한 가장 간단한 근사는 다음과 같다.
이 근사는 ''z''에 대해 0.026의 최대 절댓값 오차를 제공한다(, 에 해당). 의 경우 ''p''를 로 바꾸고 부호를 변경한다. 약간 덜 정확한 또 다른 근사는 단일 매개변수 근사이다.
후자는 정규 분포의 손실 적분에 대한 간단한 근사를 도출하는 데 사용되었다. 이 손실 적분은 다음과 같이 정의된다.
이 근사는 오른쪽 꼬리 부분에 특히 정확하다(z≥1.4에 대해 10−3의 최대 오차). 응답 모델링 방법론(RMM, Shore, 2011, 2012)을 기반으로 하는 누적 분포 함수에 대한 매우 정확한 근사는 Shore (2005)에 나와 있다.
더 많은 근사는 오차 함수#기본 함수를 이용한 근사에서 찾을 수 있다. 특히, 누적 분포 함수 와 분위 함수 에 대해서도 전체 영역에서 작은 ''상대'' 오차는 2008년 Sergei Winitzki에 의해 명시적으로 가역적인 공식을 통해 달성된다.
4. 2. 분위수 함수
정규 분포의 분위수 함수(quantile function)는 누적 분포 함수의 역함수이다. 표준 정규 분포의 분위수 함수는 프로빗 함수라고 하며, 역 오차 함수로 표현할 수 있다.
:
평균 와 분산 을 갖는 정규 확률 변수의 경우, 분위수 함수는 다음과 같다.
:
표준 정규 분포의 분위수(quantile) 는 일반적으로 로 표시된다. 이러한 값은 가설 검정, 신뢰 구간 구성 및 Q–Q plot에 사용된다. 정규 확률 변수 는 확률 로 를 초과하고, 확률 로 구간 밖에 위치한다. 특히, 분위수 는 1.96이므로, 정규 확률 변수는 단 5%의 경우에만 구간 밖에 위치한다.
다음 표는 확률 로 가 범위 에 위치하도록 하는 분위수 를 제공한다. 이러한 값은 표본 평균 및 정규(또는 asymptotically normal) 분포를 갖는 기타 통계적 추정량(estimator)에 대한 허용 구간(tolerance interval)을 결정하는 데 유용하다.[15]
| 0.80 | 1.281551565545 | 0.999 | 3.290526731492 |
| 0.90 | 1.644853626951 | 0.9999 | 3.890591886413 |
| 0.95 | 1.959963984540 | 0.99999 | 4.417173413469 |
| 0.98 | 2.326347874041 | 0.999999 | 4.891638475699 |
| 0.99 | 2.575829303549 | 0.9999999 | 5.326723886384 |
| 0.995 | 2.807033768344 | 0.99999999 | 5.730728868236 |
| 0.998 | 3.090232306168 | 0.999999999 | 6.109410204869 |
5. 관련 분포
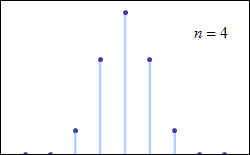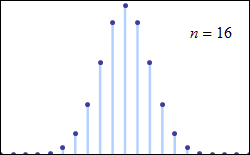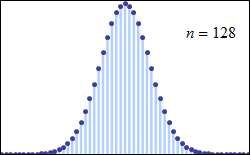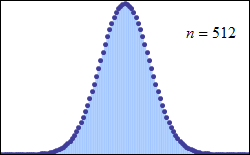
중심 극한 정리는 특정 조건에서 많은 확률 변수의 합이 근사적으로 정규 분포를 따른다고 설명한다. 이 정리는 독립적이지 않거나 동일하게 분포되지 않은 변수에도 적용될 수 있으며, 종속 정도와 분포의 적률에 특정 제약 조건이 따른다.
실제에서 접하는 많은 검정 통계량, 점수, 추정량은 특정 확률 변수의 합을 포함하며, 영향 함수를 사용하여 더 많은 추정량을 확률 변수의 합으로 나타낼 수 있다. 중심 극한 정리는 이러한 통계적 매개변수가 점근적으로 정규 분포를 가질 것임을 의미한다.
중심 극한 정리는 또한 특정 분포를 정규 분포로 근사할 수 있음을 의미한다. 예를 들어:
- 이항 분포는 표본 크기가 크고 성공 확률이 0 또는 1에 너무 가깝지 않은 경우 근사적으로 정규 분포를 따른다.
- 푸아송 분포는 모수가 큰 경우 근사적으로 정규 분포를 따른다.[37]
- 카이제곱 분포는 자유도가 큰 경우 근사적으로 정규 분포를 따른다.
- 스튜던트 t-분포는 자유도가 클 때 근사적으로 정규 분포를 따른다.
이러한 근사의 정확도는 근사가 필요한 목적과 정규 분포로의 수렴 속도에 따라 달라진다. 일반적으로 분포의 꼬리 부분에서 덜 정확하다. 베리-에센 정리는 중심 극한 정리의 근사 오차에 대한 일반적인 상한을 제공하며, 에지워스 전개는 근사의 개선을 제공한다.
이 정리는 많은 균일 잡음 소스의 합을 가우시안 잡음으로 모델링하는 것을 정당화하는 데에도 사용될 수 있다.
5. 1. 중심 극한 정리
중심 극한 정리는 특정 조건에서 많은 확률 변수의 합이 근사적으로 정규 분포를 따른다는 것을 의미한다. 독립적이고 동일한 분포를 따르는 확률 변수 이 평균 0과 분산 을 가질 때, 으로 스케일 조정된 평균인 의 확률 분포는 이 증가함에 따라 평균 0과 분산 을 갖는 정규 분포에 가까워진다.[84]
이 정리는 종속성과 분포의 적률에 특정 제약 조건이 있는 경우, 독립적이지 않거나 동일하게 분포되지 않은 변수로 확장될 수 있다. 많은 검정 통계량, 점수, 추정량은 확률 변수의 합을 포함하며, 영향 함수를 통해 더 많은 추정량을 확률 변수의 합으로 나타낼 수 있다. 중심 극한 정리는 이러한 통계적 매개변수가 점근적으로 정규 분포를 갖는다는 것을 보여준다.
중심 극한 정리는 또한 특정 분포를 정규 분포로 근사할 수 있게 한다. 예를 들면 다음과 같다.
- 이항 분포 는 이 크고 가 0 또는 1에 너무 가깝지 않은 경우 근사적으로 정규 분포를 가지며, 평균은 , 분산은 이다.
- 모수 의 푸아송 분포는 가 큰 경우 평균 와 분산 를 갖는 근사적으로 정규 분포를 따른다.[37]
- 카이제곱 분포 는 가 큰 경우 평균 와 분산 를 갖는 근사적으로 정규 분포를 따른다.
- 스튜던트 t-분포 는 가 클 때 평균 0과 분산 1을 갖는 근사적으로 정규 분포를 따른다.
이러한 근사의 정확도는 근사가 필요한 목적과 정규 분포로의 수렴 속도에 따라 달라진다. 일반적으로 분포의 꼬리 부분에서 덜 정확하다. 베리-에센 정리는 중심 극한 정리의 근사 오차에 대한 일반적인 상한을 제공하며, 에지워스 전개는 근사를 개선한다.
"독립 동일 분포를 따르는 확률 변수 의 값의 산술 평균 의 확률 분포는, 에 표준 편차가 존재한다면, 의 분포의 모양에 관계없이, 이 한없이 커졌을 때 정규 분포에 수렴한다"라는 정리이다.[84]
이 때문에 대표본의 "평균값"의 통계에는 정규 분포가 가정되는 경우가 많다. 단, "확률 변수 의 값" 자체는 을 아무리 늘려도 의 분포를 따를 뿐, 정규 분포에 수렴하는 일은 없다. 예를 들어, 하나의 주사위를 던졌을 때 눈의 분포는 주사위를 아무리 많이 던져도 1부터 6의 균등 분포이다. 정규 분포에 수렴하는 것은 나온 눈의 평균값의 분포이다.
5. 2. 정규 분포와 관련된 연산
하나 이상의 독립 또는 상관 정규 변수의 모든 함수의 확률 밀도, 누적 분포, 및 역 누적 분포는 레이 트레이싱[38]의 수치적 방법으로 계산할 수 있다. 다음은 몇 가지 특수한 경우이다.
만약 가 평균 와 분산 를 갖는 정규 분포를 따른다면:
- 임의의 실수 와 에 대해 또한 정규 분포를 따르며, 평균은 이고 분산은 이다. 즉, 정규 분포군은 선형 변환에 대해 닫혀 있다.
- 의 지수는 로그 정규 분포를 따른다: .
- 의 표준 시그모이드는 로짓 정규 분포를 따른다: .
- 의 절댓값은 접힌 정규 분포를 가진다. 만약 이면, 이는 반 정규 분포라고 알려져 있다.
- 정규화된 잔차의 절댓값인 는 자유도 1인 카이 분포를 따른다: .
- 의 제곱은 자유도 1인 비중심 카이제곱 분포를 따른다: . 만약 이면, 이 분포는 간단히 카이제곱 분포라고 불린다.
- 정규 변수 의 로그 우도는 단순히 해당 확률 밀도 함수의 로그이다: 이는 표준 정규 변수의 스케일 조정 및 이동된 제곱이므로, 스케일 조정 및 이동된 카이제곱 분포 변수로 분포된다.
- 구간 로 제한된 변수 의 분포는 절단 정규 분포라고 불린다.
- 는 위치 0과 척도 를 갖는 레비 분포를 가진다.
- 독립적인 정규 변량의 모든 선형 결합은 정규 변량이다.
- 만약 이 독립적인 표준 정규 확률 변수라면, 그 제곱의 합은 자유도를 갖는 카이제곱 분포를 따른다:
- 만약 이 평균 와 분산 을 갖는 독립적인 정규 분포 확률 변수라면, 그들의 표본 평균은 표본 표준 편차와 독립적이며,[41] 이는 바수 정리 또는 코크란 정리를 사용하여 증명할 수 있다.[42] 이 두 양의 비율은 자유도를 갖는 스튜던트 t-분포를 따를 것이다:
- 만약 , 이 독립적인 표준 정규 확률 변수라면, 그들의 정규화된 제곱합의 비율은 F-분포를 따르며, 자유도는 이다:[43]
- 정규 벡터의 이차 형식, 즉 여러 개의 독립 또는 상관된 정규 변수의 이차 함수 는 일반화된 카이제곱 분포 변수이다.
분할 정규 분포는 서로 다른 정규 분포의 밀도 함수의 크기가 조절된 부분을 결합하고, 밀도가 1이 되도록 재조정하는 것으로 가장 직접적으로 정의된다. 절단 정규 분포는 단일 밀도 함수의 일부를 재조정하여 얻는다.
정규 분포는 재생성을 갖는다. 즉, 확률 변수 이 독립적으로 각각 정규 분포 를 따른다면, 그 선형 결합 또한 정규 분포 를 따른다.
6. 통계적 추론
정규 분포는 t-분포나 F-분포와 같은 여러 분포의 기본이 될 뿐만 아니라, 실제 통계적 추론에서도 가설 검정, 구간 추정 등 다양한 상황에서 활용된다.
정규 분포 를 따르는 확률 변수 가 주어졌을 때, 로 표준화하면 확률 변수 는 표준 정규 분포를 따른다. 대학 수준의 통계학 입문 수업에서 반드시 수행하는 과정이며, 값을 구함으로써 '''표준 정규 분포표'''라고 불리는 변수에 대응하는 확률을 나타내는 일람표를 이용하여 컴퓨터 없이 정규 분포를 따르는 사건의 확률을 구할 수 있다.
불연속 값을 갖는 확률 변수에 대한 검정의 경우에도 연속 변수와 유사한 방식으로 정규 분포를 근사적으로 사용할 수 있다. 이는 표본의 크기 이 크고 데이터의 계급 폭이 좁을수록 근사의 정확도가 높아진다.
어떤 현상에 대해 법칙성을 찾거나 이론을 구축하려 할 때, 그 확률 분포가 아직 알려지지 않은 경우, 정규 분포라고 가정하여 추론하는 경우가 드물지 않지만, 잘못된 결론에 도달할 가능성이 있다. 표본 데이터가 정규 분포에 근사하는지 판단하기 위해서는 첨도와 왜도를 조사하거나, 히스토그램을 보거나, 정규 Q-Q 플롯을 확인하거나, 샤피로-윌크 검정이나 콜모고로프-스미르노프 검정(정규 분포)을 이용하는 방법 등이 일반적으로 사용된다.
정규 분포 에서 무작위 표본 를 추출할 때, 평균 에서 벗어나는 정도가 이하의 범위에 가 포함될 확률은 68.27%, 이하면 95.45%, 그리고 이면 99.73%가 된다.[84]
| 신뢰 구간 | 신뢰도 | 위험률 | ||
|---|---|---|---|---|
| 백분율 | 백분율 | 비율 | ||
| 0.318 639 | 25% | 75% | ||
| 0.674490 | 50% | 50% | ||
| 0.994458 | 68% | 32% | ||
| 1 | 68.2689492% | 31.7310508% | ||
| 1.281552 | 80% | 20% | ||
| 1.644854 | 90% | 10% | ||
| 1.959964 | 95% | 5% | ||
| 2 | 95.4499736% | 4.5500264% | ||
| 2.575829 | 99% | 1% | ||
| 3 | 99.7300204% | 0.2699796% | ||
| 3.290527 | 99.9% | 0.1% | ||
| 3.890592 | 99.99% | 0.01% | ||
| 4 | 99.993666% | 0.006334% | ||
| 4.417173 | 99.999% | 0.001% | ||
| 4.5 | 0.0006795346249% | |||
| 4.891638 | 99.9999% | 0.0001% | ||
| 5 | 99.9999426697% | 0.0000573303% | ||
| 5.326724 | 99.99999% | 0.00001% | ||
| 5.730729 | 99.999999% | 0.000001% | ||
| 99.9999998027% | 0.0000001973% | |||
| 6.109410 | 99.9999999% | 0.0000001% | ||
| 6.466951 | 99.99999999% | 0.00000001% | ||
| 6.806502 | 99.999999999% | 0.000000001% | ||
| 7 | 99.9999999997440% | 0.000000000256% |
6. 1. 모수 추정
정규 분포의 모수를 알지 못하고, 대신 이를 추정하려는 경우가 많다. 즉, 정규 모집단에서 추출한 표본 이 있을 때, 모수 와 의 근사값을 알고자 한다. 이 문제에 대한 표준적인 접근 방식은 로그 우도 함수를 최대화해야 하는 최대 우도 방법이다.와 에 대해 미분하고, 결과로 얻은 1차 조건 시스템을 풀면 최대 우도 추정량이 생성된다.
그러면 은 다음과 같다.
평균의 표준 오차도 참고
추정량 는 모든 관측치의 산술 평균이므로 표본 평균이라고 한다. 통계량 는 에 대해 완전 통계량이며 충분 통계량이므로, 레만-셰페 정리에 따라 는 균일 최소 분산 불편 추정량 (UMVU)이다.[50] 유한 표본에서 정규 분포를 따른다.
이 추정량의 분산은 역 피셔 정보 행렬 의 ''μμ''-원소와 같다. 이는 이 추정량이 효율적인 추정량임을 의미한다. 실용적으로 중요한 사실은 의 표준 오차가 에 비례한다는 것이다. 즉, 표준 오차를 10분의 1로 줄이려면 표본의 점 수를 100배 늘려야 한다. 이 사실은 여론 조사에 대한 표본 크기 결정과 몬테카를로 시뮬레이션의 시행 횟수 결정에 널리 사용된다.
점근 이론 (통계학)의 관점에서 볼 때, 는 일치 추정량이다. 즉, 일 때 로 확률 수렴한다. 또한, 이 추정량은 점근적 정규성을 가지며, 이는 유한 표본에서 정규적이라는 사실의 간단한 따름 정리이다.
추정량 는 표본의 분산()이므로 표본 분산이라고 불린다. 실제로는 대신 다른 추정량을 사용하는 경우가 많다. 이 다른 추정량은 로 표시되며, 이것 또한 표본 분산이라고 불리며 용어의 모호성을 나타낸다. 그 제곱근 는 표본 표준 편차라고 불린다. 추정량 는 분모에 ''n'' 대신 을 가진다는 점에서 와 다르다(소위 베셀의 수정):
와 의 차이는 큰 ''n''에 대해서는 무시할 정도로 작아진다. 그러나 유한 표본에서 를 사용하는 이유는 가 편향되어 있는 반면, 는 기본 매개변수 의 불편 추정량이기 때문이다. 또한, 레만-셰페 정리에 의해 추정량 는 균일 최소 분산 불편(UMVU)이며,[50] 이는 모든 불편 추정량 중에서 "최고"의 추정량임을 나타낸다. 그러나 편향된 추정량 가 평균 제곱 오차 (MSE) 기준에서 보다 낫다는 것을 보일 수 있다. 유한 표본에서 와 는 모두 자유도를 갖는 카이제곱 분포를 따른다.
이 식의 첫 번째 식은 의 분산이 와 같고, 이는 역 피셔 정보 행렬 의 ''σσ'' 요소보다 약간 크다는 것을 보여준다. 따라서 는 에 대한 효율적인 추정량이 아니며, 더 나아가 가 UMVU이므로 에 대한 유한 표본 효율 추정량은 존재하지 않는다고 결론지을 수 있다.
점근 이론을 적용하면 두 추정량 와 는 모두 일치 추정량, 즉 표본 크기 로 갈 때 확률적으로 로 수렴한다. 두 추정량은 모두 점근적으로 정규 분포를 따른다.
특히 두 추정량 모두 에 대해 점근적으로 효율적이다.
독립 동일 분포(i.i.d.)를 따르는 크기 ''n''의 정규 분포 데이터 포인트 집합 '''X'''에 대해, 각 개별 포인트 ''x''가 을 따르고 분산 σ2이 알려진 경우, 공액 사전 분포도 정규 분포를 따른다.
이는 분산을 정밀도로 재작성하여 더 쉽게 나타낼 수 있다. 즉, τ = 1/σ2을 사용한다. 그러면 이고 이면 다음과 같이 진행한다.
먼저, 우도 함수는 (평균으로부터의 차이의 합에 대한 위의 공식을 사용하여) 다음과 같다.
그런 다음, 다음과 같이 진행한다.
위의 유도 과정에서, 두 개의 이차식의 합에 대한 위의 공식을 사용했고, ''μ''를 포함하지 않는 모든 상수 인자를 제거했다. 결과는 평균이 이고 정밀도가 인 정규 분포의 커널이다. 즉,
이는 사전 매개변수와 관련하여 사후 매개변수에 대한 일련의 베이즈 업데이트 방정식으로 작성할 수 있다.
즉, 총 정밀도가 ''nτ''인 (또는 동등하게, 총 분산이 ''n''/''σ''2인) ''n''개의 데이터 포인트와 값의 평균 을 결합하려면, 데이터의 총 정밀도를 사전 총 정밀도에 더하여 새로운 총 정밀도를 구하고, 각 데이터와 관련된 총 정밀도로 가중치를 부여한 데이터 평균과 사전 평균의 가중 평균인 ''정밀도 가중 평균''을 통해 새로운 평균을 형성한다. 정밀도가 관측의 확실성을 나타낸다고 생각하면 이는 논리적으로 타당하다. 사후 평균의 분포에서 각 입력 구성 요소는 해당 확실성에 의해 가중되며, 이 분포의 확실성은 개별 확실성의 합이다. (이것에 대한 직관은 "전체는 부분의 합보다 크다(또는 작다)"라는 표현과 비교해 보라. 또한 사후 지식은 사전 지식과 우도의 조합에서 나오므로, 구성 요소보다 더 확실하다는 것은 합리적이다.)
위의 공식은 정밀도와 관련하여 정규 분포에 대한 공액 사전 분포의 베이즈 분석을 수행하는 것이 더 편리한 이유를 보여준다. 사후 정밀도는 사전 및 우도 정밀도의 합이며, 사후 평균은 위에서 설명한 대로 정밀도 가중 평균을 통해 계산된다. 동일한 공식은 모든 정밀도를 역으로 하여 분산과 관련하여 작성할 수 있으며, 더 보기 흉한 공식이 생성된다.
독립 동일 분포를 따르는 크기 ''n''의 데이터 포인트 집합 '''X'''에 대해, 각 개별 점 ''x''가 를 따르며 알려진 평균 μ를 갖는 경우, 분산의 공액 사전 분포는 역 감마 분포 또는 스케일링된 역 카이제곱 분포를 갖는다. 두 분포는 서로 다른 모수화를 제외하고 동일하다. 역 감마 분포가 더 일반적으로 사용되지만, 편의상 스케일링된 역 카이제곱 분포를 사용한다. σ2에 대한 사전 분포는 다음과 같다.
위에서 얻은 가능도 함수는 분산의 관점에서 다음과 같이 작성된다.
여기서
그런 다음:
위의 내용은 또한 스케일링된 역 카이제곱 분포이며, 여기서
또는 동등하게
역 감마 분포의 관점에서 재매개변수화하면 결과는 다음과 같다.
데이터 점 '''X'''의 크기가 ''n''이고 각 개별 점 ''x''가 를 따르며, 평균 μ와 분산 σ2를 알 수 없는 일련의 독립 동일 분포(i.i.d.) 정규 분포 데이터에 대해, 결합된 (다변량) 켤레 사전 분포가 평균과 분산 위에 배치되며, 이는 정규-역감마 분포로 구성된다.
논리적으로, 이것은 다음과 같이 시작된다.
# 알 수 없는 평균과 알려진 분산의 경우를 분석하면, 업데이트 방정식이 데이터 점의 평균과 데이터 점의 총 분산으로 구성된 데이터에서 계산된 충분 통계량을 포함하고, 이는 차례로 알려진 분산을 데이터 점 수로 나눈 값에서 계산된다.
# 알 수 없는 분산과 알려진 평균의 경우를 분석하면, 업데이트 방정식이 데이터 점 수와 제곱 편차 합으로 구성된 데이터에 대한 충분 통계량을 포함하고 있음을 알 수 있다.
# 사후 업데이트 값은 추가 데이터가 처리될 때 사전 분포 역할을 한다는 것을 명심해야 한다. 따라서, 가능한 한 동일한 의미를 유지하면서 방금 설명한 충분 통계량 측면에서 사전 분포에 대해 논리적으로 생각해야 한다.
# 평균과 분산이 모두 알 수 없는 경우, 평균과 분산 위에 독립적인 사전 분포를 배치할 수 있으며, 평균의 고정된 추정치, 총 분산, 분산 사전 분포를 계산하는 데 사용된 데이터 점의 수, 제곱 편차 합을 사용할 수 있다. 그러나 실제로는 평균의 총 분산이 알 수 없는 분산에 의존하고, 분산 사전 분포에 들어가는 제곱 편차 합이 알 수 없는 평균에 의존한다는 점에 유의해야 한다. 실제로, 후자의 의존성은 상대적으로 중요하지 않다. 실제 평균을 이동하면 생성된 점이 동일한 양만큼 이동하고 평균적으로 제곱 편차는 동일하게 유지된다. 그러나 평균의 총 분산의 경우에는 그렇지 않다. 알 수 없는 분산이 증가함에 따라 평균의 총 분산도 비례적으로 증가하며, 이 의존성을 포착하고 싶다.
# 이것은 사전 분포와 관련된 가상 관측의 평균을 지정하는 하이퍼파라미터와 가상 관측의 수를 지정하는 다른 매개변수를 사용하여 알 수 없는 분산에 대한 평균의 ''조건부 사전 분포''를 생성할 것을 제안한다. 이 수는 분산에 대한 스케일링 매개변수 역할을 하여, 실제 분산 매개변수에 대한 평균의 전체 분산을 제어할 수 있게 한다. 분산에 대한 사전 분포도 두 개의 하이퍼파라미터를 가지며, 하나는 사전 분포와 관련된 가상 관측의 제곱 편차 합을 지정하고 다른 하나는 다시 가상 관측의 수를 지정한다. 각 사전 분포는 가상 관측의 수를 지정하는 하이퍼파라미터를 가지며, 각 경우 이는 해당 사전 분포의 상대 분산을 제어한다. 이들은 두 개의 별도 하이퍼파라미터로 제공되므로 두 사전 분포의 분산(또는 신뢰도)을 개별적으로 제어할 수 있다.
# 이것은 정의된 두 분포의 곱인 정규-역감마 분포로 바로 이어지며, 켤레 사전 분포가 사용되고 (분산에 대한 역감마 분포와 분산에 ''조건부''인 평균에 대한 정규 분포) 방금 정의된 동일한 네 개의 매개변수를 사용한다.
사전 분포는 일반적으로 다음과 같이 정의된다.
업데이트 방정식은 유도될 수 있으며 다음과 같다.
각각의 가상 관측 수는 실제 관측 수를 더한다. 새로운 평균 하이퍼파라미터는 다시 가중 평균이며, 이번에는 상대 관측 수에 의해 가중된다. 마지막으로, 에 대한 업데이트는 알려진 평균의 경우와 유사하지만, 이 경우 제곱 편차 합은 실제 평균 대신 관측된 데이터 평균에 대해 취해지며, 결과적으로 사전 분포와 데이터 평균 간의 편차에서 비롯된 추가 오류 소스를 처리하기 위해 새로운 상호 작용 항을 추가해야 한다.
6. 2. 가설 검정
정규성 검정은 주어진 데이터 집합 {''x''1, ..., ''x''n''}이 정규 분포에서 나왔을 가능성을 평가하는 방법이다. 일반적으로 귀무 가설 ''H''0은 관측치가 지정되지 않은 평균 ''μ''와 분산 ''σ''2를 가진 정규 분포를 따른다는 것이며, 대립 가설 ''Ha''는 분포가 임의적이라는 것이다. 이 문제에 대해 40개 이상의 많은 검정이 고안되었으며, 그중 더 두드러진 검정은 다음과 같다.'''진단 플롯'''은 직관적이지만, 귀무 가설을 수용하거나 기각하기 위해 비공식적인 인간의 판단에 의존하므로 주관적이다.
- Q-Q 플롯(정규 확률도 또는 랭킷 플롯이라고도 함) — 데이터 집합에서 정렬된 값을 표준 정규 분포에서 해당 분위수의 예상 값에 대해 플롯한 것이다. 즉, 플롯 포인트 ''pk''가 ''pk'' = (''k'' − ''α'')/(''n'' + 1 − 2''α'')와 같고 ''α''가 0과 1 사이의 조정 상수인 (Φ−1(''pk''), ''x''(''k'')) 형태의 점을 플롯한 것이다. 귀무 가설이 참이라면, 플롯된 점은 대략 직선 위에 놓여야 한다.
- P-P 플롯 – Q-Q 플롯과 유사하지만 훨씬 덜 자주 사용된다. 이 방법은 인 점 (Φ(''z''(''k'')), ''pk'')을 플롯하는 것으로 구성된다. 정규 분포 데이터를 위해 이 플롯은 (0, 0)과 (1, 1) 사이의 45° 선 위에 있어야 한다.
'''적합성 검정''':
''모멘트 기반 검정'':
- 다고스티노 K-제곱 검정
- 자르크-베라 검정
- 샤피로-윌크 검정: Q-Q 플롯의 선이 ''σ''의 기울기를 갖는다는 사실에 기반한다. 이 검정은 해당 기울기의 최소 제곱 추정치를 표본 분산 값과 비교하고, 이 두 양이 유의하게 다르면 귀무 가설을 기각한다.
''경험적 분포 함수를 기반으로 한 검정'':
- 앤더슨-달링 검정
- 릴리에포스 검정 (콜모고로프-스미르노프 검정의 변형)
어떤 현상에 대해 법칙성을 찾거나 이론을 구축하려 할 때, 그 확률 분포가 아직 알려지지 않은 경우, 정규 분포라고 가정하여 추론하는 경우가 드물지 않지만, 잘못된 결론에 도달할 가능성이 있다. 표본 데이터가 정규 분포에 근사하는지 판단하기 위해서는 첨도와 왜도를 조사하거나, 히스토그램을 보거나, 정규 Q-Q 플롯을 확인하거나, 샤피로-윌크 검정이나 콜모고로프-스미르노프 검정(정규 분포)을 이용하는 방법 등이 일반적으로 사용된다.
6. 3. 신뢰 구간
코크란의 정리에 따르면, 정규 분포의 경우 표본 평균 와 표본 분산 ''s''2는 독립이며, 이는 그들의 결합 분포를 고려하는 데 아무런 이득이 없음을 의미한다.[51] 이 ''t''-통계량의 분포를 역으로 하면 ''μ''에 대한 신뢰 구간을 구성할 수 있다. 유사하게, 통계량 ''s''2의 ''χ''2 분포를 역으로 하면 ''σ''2에 대한 신뢰 구간을 얻을 수 있다.[52]여기서 ''tk,p''와 는 각각 ''t''-분포와 ''χ''2-분포의 ''p''번째 분위수이다. 이 신뢰 구간은 ''신뢰 수준'' (1 - ''α'')이며, 이는 실제 값 ''μ''와 ''σ''2가 이러한 구간 밖에 있을 확률 (또는 유의 수준)이 ''α''임을 의미한다. 실제에서는 일반적으로 ''α'' = 5%를 사용하며, 95% 신뢰 구간을 얻는다. ''σ''에 대한 신뢰 구간은 ''σ''2에 대한 구간 경계의 제곱근을 취하여 구할 수 있다.
근사 공식은 와 ''s''2의 점근 분포로부터 파생될 수 있다.


