보외법
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
보외법은 수치 데이터가 없는 범위의 값을 추정하는 방법으로, 기존 데이터 포인트를 기반으로 한다. 선형 외삽, 다항식 외삽, 원뿔 곡선 외삽, 프렌치 커브 외삽, 기하학적 외삽 등 다양한 방법이 존재하며, 적용할 외삽 방법의 선택은 데이터 생성 프로세스에 대한 사전 지식에 따라 달라진다. 외삽의 품질은 해당 방법이 함수에 대해 갖는 가정에 의해 제한되며, 잘못된 가정을 적용하거나 신뢰 구간을 고려하지 않으면 부정확한 결과를 초래할 수 있다. 복소 평면에서의 외삽이나 고속 외삽과 같은 특수한 경우도 존재하며, 외삽 논증과 같은 비공식적인 추론 방식에도 활용된다.
더 읽어볼만한 페이지
- 보간법 - 선형 보간법
선형 보간법은 두 점 사이의 값을 직선으로 추정하는 방법으로, 다양한 분야에서 활용되지만 비선형 데이터에는 정확도가 낮아 다른 방법으로 대체될 수 있다. - 보간법 - 스플라인 보간법
스플라인 보간법은 주어진 데이터 점들을 부드럽게 연결하는 곡선을 생성하는 방법으로, 원래 기술 도면을 그릴 때 사용된 탄성 자에서 유래되었으며, 수학적으로는 일련의 다항식을 사용하여 곡선을 모델링하고, 3차 스플라인을 포함한 다양한 형태가 존재하며, 컴퓨터 그래픽스 등 다양한 분야에서 활용된다. - 점근 해석 - 마스터 정리
마스터 정리는 분할 정복 알고리즘의 시간 복잡도 분석 도구로서, 점화식을 세 가지 경우로 나누어 재귀 알고리즘의 효율성을 파악하고, 다양한 정렬 및 일반 알고리즘 분석에 활용되지만, 특정 조건에서는 적용이 제한될 수 있습니다. - 점근 해석 - 섭동 이론
섭동 이론은 정확히 풀리는 문제에 작은 변화가 있을 때 급수로 표현하여 근사해를 구하는 방법으로, 초기 해에 보정항을 더하는 방식으로 고전역학, 양자역학 등 다양한 분야에서 활용되며 섭동 형태와 적용 차수에 따라 구분된다.
| 보외법 |
|---|
2. 방법
어떤 보외법을 적용할 것인지는 기존 데이터 포인트를 생성한 프로세스에 대한 ''사전 지식''에 달려있다. 일부 전문가들은 보외법 평가에 인과 관계를 사용하는 것을 제안하기도 한다.[2] 예를 들어, 데이터가 연속적인지, 매끄러운지, 주기성을 가질 수 있는지 등을 고려해야 한다.
보외법은 수치 데이터를 함수에 적용하여 수치 데이터가 없는 범위 밖의 값을 추정하는 방법이다. 가장 간단한 방법으로는 선형 보간법을 데이터 범위 밖의 점에 적용하는 선형 외삽이 있다. 그 외에도 리처드슨 외삽, 에이트켄의 델타 제곱 가속법, 스테펜센 변환 등이 있다.[10]
2. 1. 선형 외삽
선형 외삽은 알려진 데이터의 끝점에서 접선을 생성하고 그 한계를 넘어 연장하는 것을 의미한다. 선형 외삽은 대략 선형 함수이거나 알려진 데이터를 크게 벗어나지 않는 그래프를 확장하는 데에만 좋은 결과를 제공한다.[2]외삽할 지점 $x_*$에 가장 가까운 두 데이터 점이 $(x_{k-1},y_{k-1})$ 및 $(x_k, y_k)$인 경우, 선형 외삽은 다음 함수를 제공한다.
:$y(x_*) = y_{k-1} + \frac{x_* - x_{k-1}}{x_{k}-x_{k-1}}(y_{k} - y_{k-1}).$
(이는 $x_{k-1} < x_* < x_k$인 경우 선형 보간과 동일하다). 포함할 데이터 점에 대해 회귀와 유사한 기법을 사용하여 선형 보간법의 기울기를 평균화하여 두 개 이상의 점을 포함하는 것이 가능하다. 이는 선형 예측과 유사하다.
수치 데이터를 함수에 적용하여 수치 데이터가 없는 범위(밖)의 값을 추정하는 방법으로, 가장 간단한 방법은 선형 보간법을 데이터 범위 밖의 점에 적용하는 선형 외삽(직선 외삽)이 있다. 그 외에도 리처드슨 외삽, 에이트켄의 델타 제곱 가속법, 스테펜센 변환 등이 있다.[10]
2. 2. 다항식 외삽
어떤 외삽 방법을 적용할 것인지에 대한 적절한 선택은 기존 데이터 포인트를 생성한 프로세스에 대한 ''사전 지식''에 달려 있다. 일부 전문가들은 외삽 방법의 평가에 인과 관계를 사용하는 것을 제안했다.[2] 중요한 질문은 예를 들어 데이터가 연속적이고, 매끄럽고, 어쩌면 주기적이라고 가정할 수 있는지 등이다.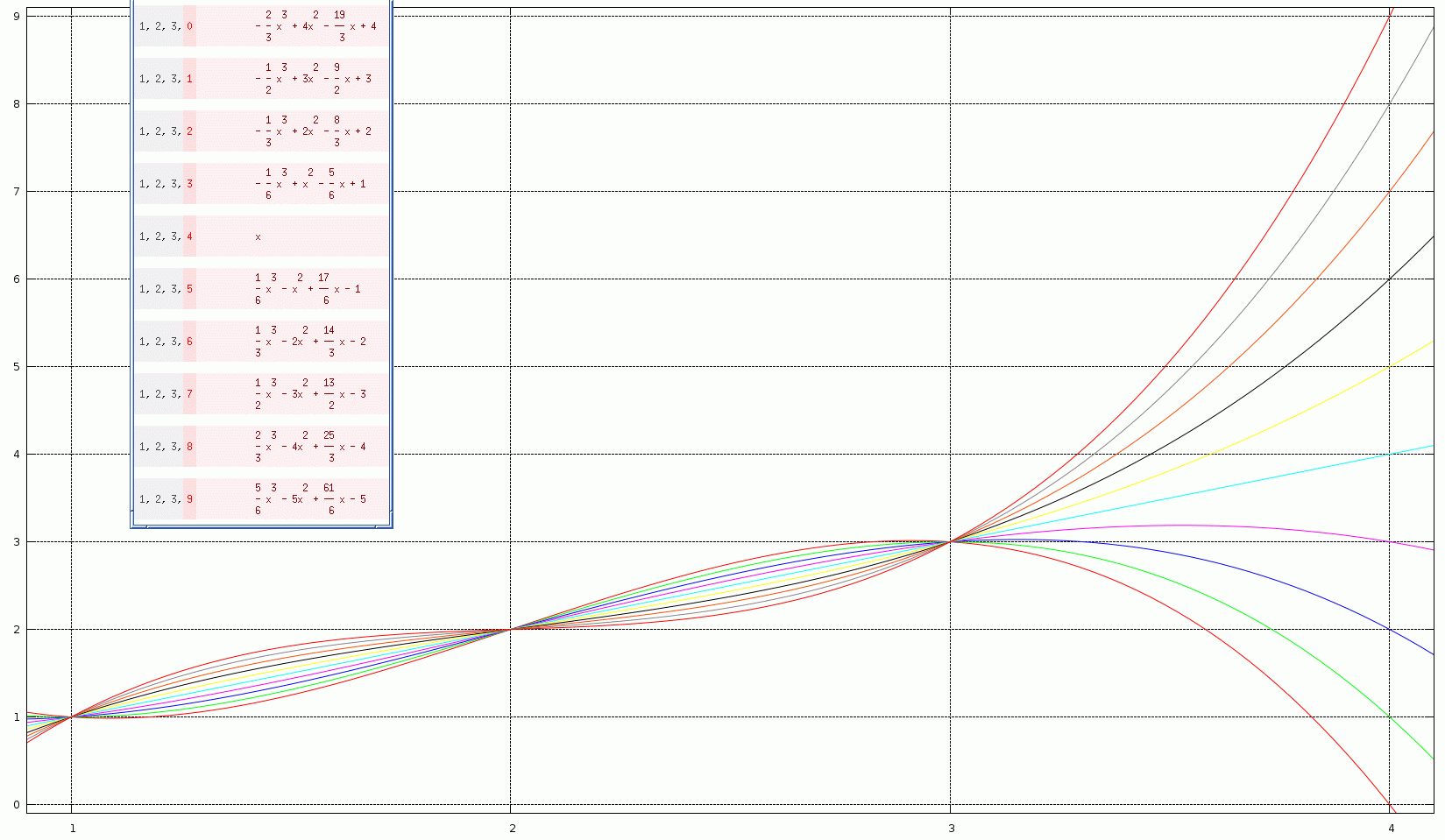
다항식 곡선은 전체 알려진 데이터를 통해 생성되거나, 끝 부분 근처에서만 생성될 수 있다(선형 외삽의 경우 두 점, 2차 외삽의 경우 세 점 등). 결과 곡선은 알려진 데이터의 끝을 넘어 확장될 수 있다. 다항식 외삽은 일반적으로 라그랑주 보간법을 사용하거나, 데이터에 맞는 뉴턴 급수를 생성하기 위해 뉴턴의 유한 차분법을 사용하여 수행된다. 결과 다항식은 데이터를 외삽하는 데 사용될 수 있다.
고차 다항식 외삽은 주의해서 사용해야 한다. 위의 그림에 있는 예제 데이터 세트 및 문제의 경우, 1차 이상(선형 외삽)은 사용 불가능한 값을 생성할 수 있다. 외삽 값의 오차 추정은 다항식 외삽의 차수와 함께 증가한다. 이는 룬게 현상과 관련이 있다.
해당 수치 데이터를 어떠한 함수에 적용하여 수치 데이터가 없는 범위(밖)의 값을 추정하는 방법이다. 가장 간단한 방법으로는 선형 보간법을 데이터 범위 밖의 점에 적용하는 외삽(선형 외삽, 직선 외삽)이 있다. 그 외에도 리처드슨 외삽, 에이트켄의 델타 제곱 가속법, 스테펜센 변환 등이 있다.[10]
2. 3. 원뿔 곡선 외삽
원뿔 곡선은 알려진 데이터의 끝 부분에 있는 다섯 개의 점을 사용하여 만들 수 있다. 생성된 원뿔 곡선이 타원 또는 원인 경우, 외삽하면 다시 루프를 돌며 자체적으로 다시 연결된다. 외삽된 포물선 또는 쌍곡선은 자체적으로 다시 연결되지는 않지만 X축을 기준으로 다시 곡선을 그릴 수 있다. 이러한 유형의 외삽은 원뿔 곡선 템플릿(종이) 또는 컴퓨터를 사용하여 수행할 수 있다.[2]2. 4. 프렌치 커브 외삽
프렌치 커브 외삽법은 지수적 경향을 띠지만 가속 또는 감속 요소를 가진 모든 분포에 적합한 방법이다.[3] 이 방법은 1987년부터 영국에서 HIV/AIDS의 성장과 변종 CJD의 예측을 제공하는 데 성공적으로 사용되었다. 또 다른 연구에 따르면, 외삽법은 더 복잡한 예측 전략과 동일한 품질의 예측 결과를 생성할 수 있다.[4]2. 5. 기하학적 외삽 (오차 예측 포함)
어떤 외삽 방법을 적용할 것인지는 기존 데이터 포인트를 생성한 프로세스에 대한 ''사전 지식''에 달려 있다. 일부 전문가들은 외삽 방법의 평가에 인과 관계를 사용하는 것을 제안했다.[2] 예를 들어 데이터가 연속적이고, 매끄럽고, 어쩌면 주기적이라고 가정할 수 있는지 등이 중요한 질문이 된다.세 점과 "모멘트" 또는 "인덱스"를 사용하여 생성할 수 있으며, 이 유형의 외삽법은 알려진 시퀀스 데이터베이스(OEIS)의 상당 부분에서 예측 정확도가 100%이다.[5]
오차 예측을 통한 외삽의 예시는 다음과 같다.
- 시퀀스 = [1, 2, 3, 5]
- f1(x, y)|f1(x, y)|영어 = x / y
- d1|d1영어 = f1(3, 2)|f1(3, 2)영어
- d2|d2영어 = f1(5, 3)|f1(5, 3)영어
- m = sequence(5)
- n = sequence(3)
- f(m, n, d1|d1영어, d2|d2영어) = round(( n * d1|d1영어 - m ) + ( m * d2|d2영어 )) = round(( 3 * 1.5 - 5 ) + ( 5 * 1.66 )) = 8
수치 데이터를 어떠한 함수에 적용하여 수치 데이터가 없는 범위(밖)의 값을 추정하는 방법이 외삽이다. 가장 간단한 방법으로는 선형 보간법을 데이터 범위 밖의 점에 적용하는 외삽(선형 외삽, 직선 외삽)이 있다. 그 외에도 리처드슨 외삽, 에이트켄의 델타 제곱 가속법, 스테펜센 변환 등이 있다.[10]
2. 6. 기타 외삽 방법
어떤 외삽 방법을 적용할 것인지에 대한 적절한 선택은 기존 데이터 포인트를 생성한 프로세스에 대한 ''사전 지식''에 달려 있다. 일부 전문가들은 외삽 방법의 평가에 인과 관계를 사용하는 것을 제안했다.[2] 중요한 질문은 예를 들어 데이터가 연속적이고, 매끄럽고, 어쩌면 주기적이라고 가정할 수 있는지 등이다.해당 수치 데이터를 어떠한 함수에 적용하여 수치 데이터가 없는 범위(밖)의 값을 추정하는 방법이다. 가장 간단한 방법으로는 선형 보간법을 데이터 범위 밖의 점에 적용하는 외삽(선형 외삽, 직선 외삽)이 있다. 그 외에도 리처드슨 외삽, 에이트켄의 델타 제곱 가속법, 스테펜센 변환 등이 있다.[10]
3. 외삽의 품질 및 한계
일반적으로 특정 외삽법의 품질은 해당 방법이 함수에 대해 갖는 가정에 의해 제한된다. 만약 해당 방법이 데이터가 매끄럽다고 가정한다면, 매끄럽지 않은 함수는 제대로 외삽되지 않을 것이다.
복잡한 시계열과 관련하여, 일부 전문가들은 인과적 힘의 분해를 통해 외삽을 수행할 때 더 정확하다는 것을 발견했다.[6]
함수에 대한 적절한 가정이 있더라도, 외삽은 함수로부터 심하게 벗어날 수 있다. 고전적인 예는 sin(''x'') 및 관련 삼각 함수의 잘린 멱급수 표현이다. 예를 들어, ''x'' = 0 근처의 데이터만 취하면, 함수가 sin(''x'') ~ ''x''처럼 동작한다고 추정할 수 있다. ''x'' = 0 근처에서 이것은 훌륭한 추정이다. 그러나 ''x'' = 0에서 멀어지면, 외삽은 sin(''x'')가 구간 [-1, 1]에 있는 동안 임의로 ''x''-축에서 멀어진다. 즉, 오차가 무한정 증가한다.
''x'' = 0 주변의 sin(''x'') 멱급수에서 더 많은 항을 사용하면 ''x'' = 0 근처의 더 넓은 구간에서 더 나은 일치를 얻을 수 있지만, 선형 근사보다 훨씬 빠르게 ''x''-축에서 벗어나는 외삽을 생성할 것이다.
이러한 발산은 외삽 방법의 특정 속성이며, 외삽 방법이 가정하는 함수 형태가 (의도하지 않게 또는 추가 정보로 인해 의도적으로) 외삽되는 함수의 본질을 정확하게 나타낼 때만 피할 수 있다. 특정 문제의 경우, 이러한 추가 정보를 사용할 수 있지만, 일반적인 경우에는 실용적인 작은 집합의 잠재적 동작으로 모든 가능한 함수 동작을 만족시키는 것은 불가능하다.
외삽의 신뢰성은 예측 신뢰 구간으로 표시된다. 예측 신뢰 구간은 이론적으로 가질 수 없는 값을 포함할 수 있으며, 이러한 경우 외삽 결과를 그대로 사용하는 것은 잘못된 결과를 초래할 수 있다. 예를 들어, 유한한 값만 가지는 변수에 대해 무한대를 정의역으로 포함하는 함수(일차 함수 등)를 선택하는 경우가 이에 해당한다.[11]
- 새로운 질병의 사망률은 처음에는 급격히 상승할 수 있다. 이때, 사망률 그래프를 선형적으로 외삽하면, 인구 전체가 수년 내에 이 질병으로 사망한다는 결과를 초래할 수 있다. 실제로는, 환자가 사망한 후, 생존자는 이 질병에 걸리는 것을 피하는 행동을 하게 되므로, 새롭게 발견된 질병의 사망률은 감소한다. 더 나아가, 생존자가 처음부터 이 질병에 대해 면역을 가지고 있을 수도 있고, 질병의 유행에 직면함으로써 후천적으로 면역을 얻을 수도 있다. 질병의 유행과 사망률 상승에 따라, 치료법도 발전할 수 있다.
- 호수의 수량이 시간이 지남에 따라 감소하는 경우 선형 외삽을 수행하면, 어떤 미래 시점에서 수량이 0이 된다. 그 이후 기간은 마이너스 수량이 예측되지만, 이는 비합리적이다.
4. 복소 평면에서의 외삽
복소해석학에서 외삽법 문제는 변수 변환 ẑ|제트영어 = 1/z을 통해 보간법 문제로 변환될 수 있다. 이 변환은 복소 평면 내의 단위원 부분을 복소 평면 외부 부분과 교환한다. 특히, 콤팩트화 무한대 점은 원점으로, 원점은 무한대로 매핑된다. 하지만 이 변환에는 주의를 기울여야 하는데, 원래 함수가 샘플링된 데이터로는 나타나지 않는 무한대에서 극점과 다른 수학적 특이점과 같은 "특징"을 가질 수 있기 때문이다.
또 다른 외삽법 문제는 해석적 연속 문제와 느슨하게 관련되어 있는데, (일반적으로) 함수의 멱급수 표현이 수렴하는 한 지점에서 확장되어 더 큰 수렴 반경을 갖는 멱급수를 생성한다. 즉, 작은 영역의 데이터 집합을 사용하여 함수를 더 큰 영역으로 외삽한다.
해석적 연속은 초기 데이터에서는 나타나지 않는 함수의 특징에 의해 방해받을 수 있다.
또한, 파데 근사 및 레빈형 수열 변환과 같은 수열 변환을 외삽 방법으로 사용하여 원래의 수렴 반경 밖에서 발산하는 멱급수의 합을 구할 수 있다. 이 경우, 종종 유리 근사를 얻는다.
5. 고속 외삽
추출된 데이터는 종종 커널 함수로 합성된다. 데이터가 추출된 후 데이터의 크기는 N배 증가하며, 여기서 N은 대략 2~3이다. 이 데이터를 알려진 커널 함수로 합성해야 하는 경우, 고속 푸리에 변환(FFT)을 사용하더라도 수치 계산이 Nlog(N)배 증가한다. 추출된 데이터의 일부에 대한 기여도를 분석적으로 계산하는 알고리즘이 존재한다. 계산 시간은 원래 합성곱 계산과 비교하여 생략될 수 있다. 따라서 이 알고리즘을 사용하면 추출된 데이터를 사용한 합성곱 계산이 거의 증가하지 않는다. 이를 고속 추출이라고 한다. 고속 추출은 CT 영상 재구성에 적용되었다.[7]
6. 외삽 논증
확장 주장은 사실로 알려진 값의 범위를 넘어선 무언가가 아마도 사실일 것이라고 주장하는 비공식적이고 정량화되지 않은 주장이다. 예를 들어, 사람들은 확대경을 통해 보는 것의 현실을 믿는다. 왜냐하면 그것은 육안으로 보는 것과 일치하지만 그 범위를 넘어서기 때문이다. 사람들은 광학 현미경을 통해 보는 것을 믿는다. 왜냐하면 그것은 확대경을 통해 보는 것과 일치하지만 그 범위를 넘어서기 때문이다. 전자 현미경도 마찬가지이다. 이러한 주장은 생물학에서 동물 연구에서 인간으로, 예비 연구에서 더 광범위한 집단으로 확장하는 데 널리 사용된다.[8]
미끄러운 경사 주장과 마찬가지로, 확장 주장은 알려진 범위를 얼마나 넘어 확장되는지 등의 요인에 따라 강하거나 약할 수 있다.[9]
7. 잘못된 사용 예
외삽법의 신뢰성은 예측 신뢰 구간으로 표시된다. 예측 신뢰 구간은 이론적으로 불가능한 값을 포함할 수 있으며, 이러한 경우 외삽 결과를 그대로 사용하면 잘못된 결과를 초래할 수 있다. 예를 들어, 유한한 값만 가지는 변수에 대해 무한대를 정의역으로 포함하는 함수(일차 함수 등)를 선택하는 경우가 이에 해당한다.[11]
- 새로운 질병의 사망률은 처음에는 급격히 상승할 수 있다. 이때, 사망률 그래프를 선형적으로 외삽하면, 인구 전체가 수년 내에 이 질병으로 사망한다는 잘못된 결과를 낼 수 있다. 실제로는 환자가 사망한 후, 생존자는 이 질병을 피하는 행동을 하게 되므로, 새롭게 발견된 질병의 사망률은 감소한다. 또한, 생존자가 처음부터 이 질병에 대해 면역을 가지고 있거나, 질병 유행에 직면하여 후천적으로 면역을 얻을 수도 있다. 질병의 유행과 사망률 상승에 따라, 치료법도 발전할 수 있다.
- 호수의 수량이 시간이 지남에 따라 감소하는 경우 선형 외삽을 수행하면, 특정 미래 시점에 수량이 0이 된다는 예측이 가능하다. 그러나 그 이후 기간은 마이너스 수량이 예측되는데, 이는 비합리적이다.
참조
[1]
웹사이트
Extrapolation
http://www.merriam-w[...]
[2]
논문
Causal Forces: Structuring Knowledge for Time-series Extrapolation
https://repository.u[...]
2012-01-10
[3]
웹사이트
AIDSCJDUK.info Main Index
http://www.AIDSCJDUK[...]
[4]
논문
Forecasting by Extrapolation: Conclusions from Twenty-Five Years of Research
https://repository.u[...]
2012-01-10
[5]
웹사이트
Probnet: Geometric Extrapolation of Integer Sequences with error prediction
https://hackage.hask[...]
2023-03-14
[6]
논문
Decomposition by Causal Forces: A Procedure for Forecasting Complex Time Series
https://repository.u[...]
[7]
논문
Reconstruction from truncated projections using mixed extrapolations of exponential and quadratic functions.
https://web.archive.[...]
2014-06-03
[8]
서적
Across the Boundaries: Extrapolation in Biology and Social Science
https://oxford.unive[...]
Oxford University Press
2007
[9]
논문
Arguments whose strength depends on continuous variation
http://ojs.uwindsor.[...]
2021-06-29
[10]
서적
Cで学ぶ数値計算アルゴリズム
共立出版
[11]
서적
Identification Problems in the Social Sciences
Harvard University Press
1999
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com