분산 분석

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

분산 분석(ANOVA)은 둘 이상의 그룹 간의 평균 차이를 검정하는 데 사용되는 통계적 방법이다. 이 방법은 18세기 후반부터 발전해왔으며, 로널드 피셔에 의해 "분산"이라는 용어가 도입되고 공식적인 분석이 제안되면서 널리 알려지게 되었다. 분산 분석은 실험 설계, 특히 대상에 대한 처치의 무작위 할당을 기반으로 하며, 고정 효과, 무선 효과, 혼합 효과 모형 등 다양한 모형을 사용한다. 일원 분산 분석, 이원 분산 분석, 다변량 분산 분석 등 여러 종류가 있으며, 사후 검정을 통해 구체적인 그룹 간의 차이를 확인할 수 있다. 분산 분석은 사회과학, 의학, 공학 등 다양한 분야에서 활용되며, SAS, SPSS, R 등 여러 소프트웨어를 통해 수행할 수 있다. 하지만 데이터의 정규성, 등분산성 등의 가정을 충족해야 하며, 불균형 데이터와 복잡한 사회 현상에 대한 해석에 주의를 기울여야 한다.

더 읽어볼만한 페이지

분산 분석 - 다층 모형
다층 모형은 계층 구조 데이터 분석에 사용되는 통계 방법으로, 변수의 측정 수준을 명확히 하고 고정 효과와 변량 효과를 동시에 고려하며, 무작위 절편 모형, 무작위 기울기 모형 등 다양한 종류가 있다.
분산 분석 - 등분산성
등분산성은 통계학에서 모수 추정치의 통계량들이 동일한 분산을 갖는 성질로, 고전적 회귀 모형 등에서 오차항의 분산이 모든 관찰값에 대해 동일하다는 가정이며, 바틀렛 검정 등으로 검정할 수 있다.
실험 설계 - 무작위 대조 시험
실험 설계 - 실험군과 대조군
실험군과 대조군은 임상 연구에서 새로운 방법이나 약물의 효과를 평가하기 위해 사용되는 두 그룹으로, 대조군은 비교 기준이 되며, 실험군은 새로운 치료법을 받는 그룹이다.

분산 분석
개요
학문 분야	통계학
하위 분야	실험 설계, 회귀 분석, 분산 성분 분석
다른 이름	ANOVA (Analysis of Variance)
목표
목표	둘 이상의 모집단 평균 간에 유의미한 차이가 있는지 여부를 테스트합니다. 여러 그룹 간의 평균 차이를 조사합니다.
기본 원리
기본 원리	각 그룹 내 변동과 그룹 간 변동을 비교합니다. 그룹 간 변동이 그룹 내 변동보다 충분히 크면 그룹 평균 간에 유의미한 차이가 있다고 결론 내립니다.
종류
종류	일원 분산 분석 (One-way ANOVA) 이원 분산 분석 (Two-way ANOVA) 다변량 분산 분석 (MANOVA) 반복 측정 분산 분석 (Repeated Measures ANOVA)
가정
가정	각 그룹 내 데이터가 정규 분포를 따릅니다. 각 그룹의 분산이 동일합니다 (등분산성). 데이터가 독립적입니다.
활용
활용	의학 연구: 신약의 효과 비교, 치료법 비교 마케팅: 광고 효과 비교, 제품 선호도 조사 심리학: 실험 결과 분석, 그룹 간 차이 분석 공학: 제품 성능 비교, 설계 변수 영향 분석
관련 개념
관련 개념	F-검정 t-검정 카이제곱 검정 유의 수준 p-값

2. 역사

분산 분석은 20세기에 결실을 맺었지만, 그 기원은 스티글러에 따르면 수세기 전으로 거슬러 올라간다.^[1] 여기에는 가설 검정, 제곱합의 분할, 실험 기술, 그리고 가법 모형 등이 포함된다. 로널드 피셔는 1918년 The Correlation between Relatives on the Supposition of Mendelian Inheritance 논문에서 "분산"이라는 용어를 처음 제안했으며,^[9] 1925년 저서 ''Statistical Methods for Research Workers''을 통해 분산 분석을 널리 알렸다.

2. 1. 초기 발전

분산 분석은 20세기에 결실을 맺었지만, 스티글러에 따르면 그 기원은 수세기 전으로 거슬러 올라간다.^[1] 여기에는 가설 검정, 제곱합의 분할, 실험 기술, 그리고 가법 모형이 포함된다. 1770년대에 라플라스는 가설 검정을 수행했다.^[2] 1800년경, 라플라스와 가우스는 관측값을 결합하기 위한 최소제곱법을 개발했는데, 이는 당시 천문학 및 측지학에서 사용되던 방법보다 개선된 것이었다. 또한 제곱합에 대한 많은 연구를 시작했다. 라플라스는 (전체 제곱합이 아닌) 잔차 제곱합으로부터 분산을 추정하는 방법을 알고 있었다.^[3] 1827년까지, 라플라스는 대기 조석 측정에 관한 분산 분석 문제를 해결하기 위해 최소제곱법을 사용하고 있었다.^[4] 1800년 이전에, 천문학자들은 반응 시간으로 인한 관측 오류("개인 방정식")를 분리해냈고, 오류를 줄이는 방법을 개발했다.^[5] 개인 방정식 연구에 사용된 실험 방법은 이후 새롭게 등장한 심리학 분야에서도 받아들여졌으며,^[6] 심리학은 무작위화와 블라인딩이 곧 추가된 강력한(완전 요인) 실험 방법을 개발했다.^[7] 1885년에 가법 효과 모형에 대한 명확한 비수학적 설명이 제공되었다.^[8]

로널드 피셔는 "분산"이라는 용어를 도입했으며, 1918년 이론 인구 유전학에 관한 논문인 ''The Correlation between Relatives on the Supposition of Mendelian Inheritance''에서 분산의 공식적인 분석을 제안했다.^[9] 데이터 분석에 분산 분석을 처음 적용한 것은 1921년에 발표된 ''Studies in Crop Variation I''이었다.^[10] 이 논문은 시계열의 변동을 연간 원인과 느린 악화로 나타내는 요소로 나누었다. 1923년에는 위니프레드 매켄지와 함께 ''Studies in Crop Variation II''를 출판하여, 서로 다른 품종으로 파종하고 다른 비료 처리를 받은 플롯에서 수확량의 변동을 연구했다.^[11] 분산 분석은 피셔의 1925년 저서 ''Statistical Methods for Research Workers''에 포함되면서 널리 알려지게 되었다.

무작위화 모형은 여러 연구자에 의해 개발되었다. 최초의 연구는 1923년 예르지 네이만에 의해 폴란드어로 출판되었다.^[12]

3. 기본 원리 및 가정

분산 분석(ANOVA)은 여러 집단 간의 평균 차이를 비교하는 통계적 방법이다. 기본 원리는 집단 간 분산과 집단 내 분산을 비교하는 것이다. 이를 통해 집단 간 평균 차이가 통계적으로 유의미한지 검정한다.^[15]^[16]^[17]^[18]

분산 분석은 다음과 같은 가정을 기반으로 한다.^[15]^[16]^[17]^[18]

독립성: 각 관측치는 서로 독립적이어야 한다. 이는 통계적 분석을 단순화하기 위한 가정이다.
정규성: 각 집단의 데이터는 정규 분포를 따라야 한다. 또는, 잔차의 분포가 정규 분포를 따라야 한다.
등분산성: 각 집단의 분산은 동일해야 한다. 이를 분산의 동질성(등분산성)이라고도 한다.

이러한 가정들은 오차가 독립적이고 동일한 정규 분포를 따른다는 것을 의미한다. 즉, 오차(

\varepsilon

)는 독립적이며,

\varepsilon \thicksim N(0, \sigma^2).

를 따른다.

하지만, 분산 분석의 일반적인 경우에는 위와 같은 가정이 반드시 필요하지는 않다. F 검정은 지속적인 관심사와 실질적인 제약 사항을 갖는다.

무작위 대조 실험에서 처리는 실험 단위(Unit)에 무작위로 할당되며, 이러한 무작위화는 객관적이며 실험 수행 전에 선언된다. 객관적인 무작위 할당은 찰스 샌더스 퍼스와 로널드 피셔의 아이디어를 따라 귀무 가설의 유의성을 검증하는 데 사용된다.

로섬스테드 실험 연구소의 프랜시스 J. 앤스콤과 아이오와 주립 대학교의 오스카 켐프손은 '단위 처리 가산성'을 가정하여 설계 기반 분석을 개발했다.^[19] 켐프손과 데이비드 R. 콕스는 그들의 저서에서 단위 처리 가산성에 대해 논의했다.^[20]^[21]

정규 모형 기반 분산 분석은 잔차의 독립성, 정규성, 등분산성을 가정하는 반면, 무작위화 기반 분석은 잔차의 등분산성만 가정한다(단위-처리 가산성의 결과). 두 분석 모두 등분산성을 필요로 한다.

3. 1. F 분포

F분포는 분산의 비교를 통해 얻어진 분포 비율이다.^[27] 이 비율을 이용하여 각 집단의 모집단 분산에 차이가 있는지, 또는 모집단 평균에 차이가 있는지 검정한다. F는 다음과 같이 계산된다: F = (군간변동)/(군내변동). 만약 군내변동이 크다면 집단 간 평균 차이를 확인하기 어렵다. 분산분석은 집단 간 분산의 동질성을 가정하므로, 분산 차이가 크다면 그 차이를 유발하는 변인을 찾아 제거해야 한다. 그렇지 않으면 분산분석의 신뢰도가 낮아진다.^[27]

분산 분석에서는 다음 가정을 전제로 한다.^[27]

정규성 가정: 각 모집단에서 변인 Y는 정규분포를 따른다. 각 모집단의 Y 평균은 다를 수 있다.
분산의 동질성 가정: Y의 모집단 분산은 각 모집단에서 동일하다.
관찰의 독립성 가정: 각 모집단에서 크기가 다른 표본들이 독립적으로 표집된다.

각 표본에서 산출된 모집단 분산 추정치의 비율, 즉 F = s₁² / s₂²을 구한다. 이 값을 'F' 또는 'F 통계치'라고 한다. F 값들은 특정한 이론적 확률분포를 따르는데, 이것이 바로 F 분포이다.^[27]

''F'' 검정은 총 편차의 요인을 비교하는 데 사용된다. 예를 들어, 일원 또는 단일 요인 분산 분석에서 통계적 유의성은 F 검정 통계량을 비교하여 검정한다.^[27]

F = \frac{\text{처리 간 분산}}{\text{처리 내 분산}} =

여기서 ''MS''는 평균 제곱,

I

는 처리 수,

n_T

는 총 사례 수이다.^[27]

I - 1

을 분자 자유도로,

n_T - I

를 분모 자유도로 사용하여 ''F''-분포와 비교한다. 검정 통계량이 각각 카이제곱 분포를 따르는 두 개의 스케일링된 제곱합의 비율이기 때문에 ''F''-분포를 사용하는 것은 자연스럽다.^[27]

F의 기대값은

1 + {n \sigma^2_\text{처리}} / {\sigma^2_\text{오차}}

이며(

n

은 처리 표본 크기), 처리 효과가 없는 경우 1이다. F 값이 1 이상으로 증가함에 따라 귀무 가설과 일치하지 않는 증거가 증가한다. F를 증가시키는 두 가지 명백한 실험 방법은 표본 크기를 늘리고 엄격한 실험 제어를 통해 오차 분산을 줄이는 것이다.^[27]

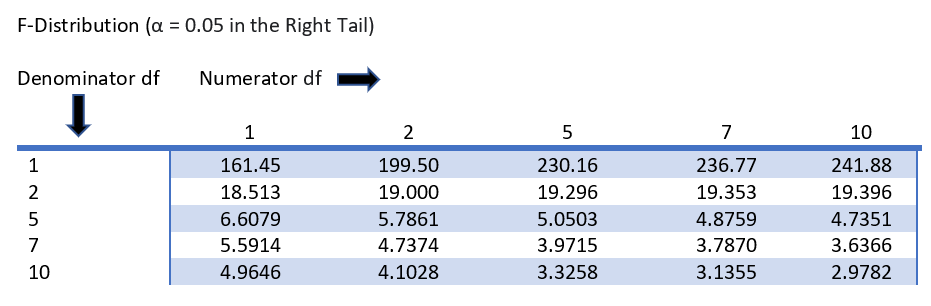
일원 분산 분석의 통계적 유의성을 확인하기 위해 자유도를 사용하여 알파 수준의 F-확률 표를 참조. F-통계량을 계산한 후, 각 자유도의 교차점에서 값을 비교하며, 이를 임계값이라고도 함. F-통계량의 크기가 임계값보다 크면, 알파 수준에서 통계적 유의성이 있다고 말할 수 있음.

ANOVA 가설 검정을 결론짓는 두 가지 방법이 있으며, 둘 다 동일한 결과를 생성한다.^[27]

교과서적인 방법은 F의 관찰된 값을 표에서 결정된 F의 임계값과 비교하는 것이다. F의 임계값은 분자와 분모의 자유도와 유의 수준(''α'')의 함수이다. F ≥ F_임계이면 귀무 가설을 기각한다.
컴퓨터 방법은 관찰된 값보다 크거나 같은 F 값의 확률(p-값)을 계산한다. 이 확률이 유의 수준(''α'') 이하이면 귀무 가설을 기각한다.

ANOVA ''F''-검정은 고정된 오차를 발생시키는 동안 제2종 오류를 최소화하는 의미에서 거의 최적임이 알려져 있다(즉, 고정된 유의 수준에 대해 검정력을 최대화). 예를 들어, 다양한 의료 치료법이 정확히 동일한 효과를 갖는지 테스트하기 위해, ''F''-검정의 ''p''-값은 순열 검정의 p-값에 가깝게 근사된다. 근사는 설계가 균형을 이룰 때 특히 가깝다.^[27]^[38] 이러한 순열 검정은 최대 검정력을 가진 검정을 모든 대립 가설에 대해 특징짓는다고 로젠바움에 의해 관찰되었다.^[39] ANOVA ''F''-검정(모든 처리가 정확히 동일한 효과를 가진다는 귀무 가설)은 많은 대립 분포에 대한 견고성 때문에 실용적인 검정으로 권장된다.^[40]^[41]

3. 2. 기본 가정

F분포는 분산의 비교를 통해 얻어진 분포 비율이다. 이 비율을 이용하여 각 집단의 모집단 분산이 차이가 있는지에 대한 검정과 모집단 평균이 차이가 있는지 검정하는 방법으로 사용한다. 즉, F = (군간 변동)/(군내 변동)이다. 만약 군내 변동이 크다면 집단 간 평균 차이를 확인하는 것이 어렵다. 분산분석에서는 집단 간의 분산의 동질성을 가정하고 있기 때문에, 만약 분산의 차이가 크다면 그 차이를 유발한 변인을 찾아 제거해야 한다. 그렇지 못하면 분산분석의 신뢰도는 나빠지게 된다.

분산 분석은 선형 모형의 관점에서 제시될 수 있으며, 이는 응답의 확률 분포에 대해 다음과 같은 가정을 한다.^[15]^[16]^[17]^[18]

정규성: 잔차의 분포는 정규 분포를 따른다.
독립성: 통계적 분석을 단순화하는 모형의 가정이다.
분산의 동일성(또는 "동질성", 등분산성): 그룹 내 데이터의 분산은 동일해야 한다.

교과서 모형의 개별 가정은 오차가 고정 효과 모형에 대해 독립적이고 동일하며 정규 분포를 따른다는 것을 의미한다. 즉, 오차(

\varepsilon

)는 독립적이며,

:

\varepsilon \thicksim N(0, \sigma^2).

분산 분석의 일반적인 경우에 필요한 가정은 없지만, 분산 분석 가설 검정에 사용되는 F 검정은 지속적인 관심사인 가정과 실질적인 제약 사항을 갖는다.

정규 모형 기반 분산 분석은 잔차의 독립성, 정규성, 등분산성을 가정한다. 무작위화 기반 분석은 잔차의 등분산성만 가정하며(단위-처리 가산성의 결과로), 실험의 무작위화 절차를 사용한다. 이 두 분석 모두 등분산성을 필요로 하는데, 정규 모형 분석의 가정으로서, 그리고 무작위화와 가산성의 결과로서 무작위화 기반 분석에 필요하다.

4. 분산 분석 모형

실험계획법에 따라 분산 분석 모형은 세 가지로 구분된다. 수준을 선택하는 방법에 따라 모수인자와 변량인자가 있으며, 이에 따라 다음과 같은 분산분석 모형이 있다.

고정 효과 모형 (Fixed-effects model, 모수 인자 모형): 실험자가 실험 대상에 하나 이상의 처리를 적용하여 반응 변수 값이 변경되는지 확인하는 상황에 적용된다.
무선 효과 모형 (Random-effects model, 변량인자 모형): 수준의 선택이 임의적으로 이루어지며 각 수준이 기술적 의미를 가지고 있지 않은 효과 인자를 사용한다. 예를 들어 원료의 종류 같은 것들이 있다.^[13]
혼합 효과 모형 (Mixed-effects model, 혼합인자 모형): 고정 효과 인자와 무선 효과 인자가 함께 사용된 경우를 말한다.^[1]

4. 1. 고정 효과 모형 (Fixed-effects model)

고정 효과 모형(Fixed-effects model, 모수 인자 모형)은 실험자가 실험 대상에 하나 이상의 처리를 적용하여 반응 변수 값이 변경되는지 확인하는 상황에 적용된다. 이를 통해 실험자는 전체 모집단에서 처리가 생성할 반응 변수 값의 범위를 추정할 수 있다.^[75]

고정 효과 인자는 수준의 선택이 기술적으로 정해져 있고 각 수준이 기술적 의미를 가지고 있는 효과 인자를 말한다. 예를 들어 온도, 압력 같은 것들이다. 모수 인자만 사용된 경우 고정 효과 모형이라고 한다. 이 경우 각 수준에서의 모평균 값의 추정에 의미를 두고 있다.

예를 들어, 대학 또는 학과에서 좋은 입문 교재를 찾기 위해 교육 실험을 수행할 수 있으며, 각 교재를 처리 방법으로 간주할 수 있다. 고정 효과 모형은 후보 교재 목록을 비교한다.

분산 분석은 선형 모형의 관점에서 제시될 수 있으며, 이는 응답의 확률 분포에 대해 다음과 같은 가정을 한다.^[15]^[16]^[17]^[18]

독립성 - 이는 통계적 분석을 단순화하는 모형의 가정이다.
정규성 - 잔차의 분포는 정규 분포를 따른다.
분산의 동일성(또는 "동질성"), 등분산성이라고 함 - 그룹 내 데이터의 분산은 동일해야 한다.

교과서 모형의 개별 가정은 오차가 고정 효과 모형에 대해 독립적이고 동일하며 정규 분포를 따른다는 것을 의미한다. 즉, 오차(

\varepsilon

)는 독립적이며,

\varepsilon \thicksim N(0, \sigma^2).

4. 2. 무선 효과 모형 (Random-effects model)

무선 효과 인자는 수준의 선택이 임의적으로 이루어지며 각 수준이 기술적 의미를 가지고 있지 않은 효과 인자를 말한다. 예를 들어 원료의 종류 같은 것들이다.^[13] 무선 효과 인자만 사용된 경우 '''무선 효과 모형'''(Random-effects model, 변량인자 모형)이라고 한다. 이 경우 각 수준은 임의적으로 결정되었기 때문에 각 수준의 모평균값 추정은 의미가 없으며, 단지 인자에 의한 산포의 정도를 추정하는 것에 의미를 두고 있다.^[13]

랜덤 효과 모형(2형)은 처치가 고정되지 않은 경우에 사용된다. 이는 다양한 요인 수준이 더 큰 모집단에서 표본 추출될 때 발생한다. 수준 자체가 확률 변수이기 때문에, 몇 가지 가정과 처치 대조 방법(단순 차이의 다변수 일반화)은 고정 효과 모형과 다르다.^[13]

대학 또는 학과에서 좋은 입문 교재를 찾기 위해 교육 실험을 수행할 수 있으며, 각 교재를 처리 방법으로 간주할 수 있다. 고정 효과 모형은 후보 교재 목록을 비교한다. 랜덤 효과 모형은 무작위로 선택된 교재 목록 간에 중요한 차이가 있는지 여부를 결정한다.^[13]

4. 3. 혼합 효과 모형 (Mixed-effects model)

'''혼합 효과 모형'''(Mixed-effects model, 혼합인자 모형)은 고정 효과 인자와 무선 효과 인자가 함께 사용된 경우를 말한다.^[1] 혼합 효과 모형은 고정 효과와 랜덤 효과 유형의 실험 요소를 모두 포함하며, 두 유형에 대해 적절히 다른 해석과 분석을 수행한다.^[1]

예를 들어, 대학 또는 학과에서 좋은 입문 교재를 찾기 위해 교육 실험을 수행할 수 있으며, 각 교재를 처리 방법으로 간주할 수 있다.^[1] 이때 고정 효과 모형은 후보 교재 목록을 비교한다.^[1] 반면 랜덤 효과 모형은 무작위로 선택된 교재 목록 간에 중요한 차이가 있는지 여부를 결정한다.^[1] 혼합 효과 모형은 (고정된) 기존 교재를 무작위로 선택된 대안과 비교한다.^[1]

고정 및 랜덤 효과를 정의하는 것은 여러 상반된 정의로 인해 파악하기 어려운 것으로 알려져 있다.^[1]

5. 분산 분석의 종류

분산 분석은 독립 변수와 종속 변수의 수, 실험 설계 방식에 따라 다양하게 분류된다.

많은 통계학자들은 분산 분석을 실험 설계를 기반으로 분류하며,^[56] 특히 대상에 대한 처치의 무작위 할당을 명시하는 프로토콜을 기반으로 한다. 할당 메커니즘에 대한 프로토콜 설명에는 처치의 구조와 모든 블록화에 대한 사양이 포함되어야 한다. 적절한 통계 모델을 사용하여 관찰 데이터에 분산 분석을 적용하는 것도 일반적이다.^[57]

일부 인기 있는 설계는 다음과 같은 유형의 분산 분석을 사용한다.

일원 분산 분석은 둘 이상의 독립 그룹(평균) 간의 차이를 테스트하는 데 사용된다. 예를 들어, 작물에 대한 다양한 수준의 요소 시비, 여러 다른 박테리아 종에 대한 항생 작용의 여러 수준,^[58] 또는 환자 그룹에 대한 일부 약물의 효과의 다른 수준 등이 있다.
요인 분산 분석은 요인이 둘 이상일 때 사용된다.
반복 측정 분산 분석은 각 요인에 대해 동일한 피험자를 사용하는 경우(예: 종단 연구) 사용된다.
다변량 분산 분석 (MANOVA)은 반응 변수가 둘 이상일 때 사용된다.

5. 1. 일원 분산 분석 (One-way ANOVA)

One-way ANOVA^영어는 하나의 독립 변수에 따른 종속 변수의 평균 차이를 검정하는 데 사용된다. 예를 들어, 학력 수준에 따른 소득 차이를 분석하는 경우가 이에 해당한다.

분산 분석(ANOVA)에서 독립 변수는 요인(factor)으로 표현되며, 종속 변인은 1개, 독립 변인의 집단도 1개인 경우를 일원 분산 분석이라고 한다. 독립 변인의 집단이 2개 이상이므로 사후 분석을 실시한다.

예시는 다음과 같다.

가구 소득(독립 변인)에 따른 식료품 소비 정도(종속 변인)의 차이를 분석할 수 있다. 가구 소득 집단은 저소득, 중산층, 고소득층 등 2개 이상으로 구분된다.
한국, 중국, 일본 3개국(독립 변인: 국적, 집단 3개) 10세 남아의 체중(종속 변인) 비교를 할 수 있다.

일반적으로 일원 분산 분석은 최소 세 그룹 간의 차이를 테스트하는 데 사용된다. 비교할 평균이 두 개뿐일 때는 t-검정과 분산 분석 ''F''-검정은 동일하며, F = t² 의 관계를 가진다.

5. 2. 이원 분산 분석 (Two-way ANOVA)

이원 분산 분석(two-way ANOVA)은 두 개 이상의 독립 변수가 종속 변수의 평균에 미치는 영향을 검정하는 데 사용되는 통계 방법이다. 이 분석 방법은 각 독립 변수의 주효과뿐만 아니라, 독립 변수 간의 상호작용 효과도 함께 분석할 수 있다는 장점이 있다.

예를 들어, 학력과 성별이 휴대폰 요금에 미치는 영향을 분석하는 경우를 생각해 보자. 이 경우 학력과 성별은 독립 변수가 되고, 휴대폰 요금은 종속 변수가 된다. 이원 분산 분석을 통해 학력과 성별 각각이 휴대폰 요금에 미치는 영향(주효과)과 더불어, 학력과 성별의 조합이 휴대폰 요금에 미치는 영향(상호작용 효과)을 파악할 수 있다.^[32]

또 다른 예로, 한국, 중국, 일본 세 국가 간에 성별과 학력에 따른 체중 비교를 하는 경우를 들 수 있다. 이 경우 독립 변수는 성별과 학력 두 가지이며, 각 독립 변수는 세 국가(한국, 중국, 일본)라는 집단을 가진다. 종속 변수는 체중이 된다.

이원 분산 분석은 여러 요인의 효과를 동시에 연구하는 데 매우 효율적이다. 특히, 요인 실험 설계에서 널리 사용되며, 여러 요인 간의 상호작용을 파악하는 데 유용하다. 하지만 상호작용이 유의미하게 나타날 경우, 결과 해석이 복잡해질 수 있으므로 주의해야 한다. "유의미한 상호작용은 종종 주 효과의 유의성을 가릴 수 있다."^[45] 따라서, 상호작용이 발견되면 그래프 등을 활용하여 시각적으로 분석하고, 필요한 경우 회귀 분석 등 추가적인 분석을 수행하는 것이 좋다.

5. 3. 다원 변량 분산 분석 (MANOVA)

다변량 분산 분석(MANOVA)은 반응 변수가 둘 이상일 때 사용된다.^[56] 이는 단순한 분산분석을 확장하여 두 개 이상의 종속 변인이 서로 관계된 상황에 적용시킨 것이다. 둘 이상의 집단 간 차이를 검증할 수 있다.

5. 4. 공분산 분석 (ANCOVA)

다원 변량 분산 분석에서 특정한 독립 변인에 초점을 맞추고 다른 독립 변인은 통제 변수로 하여 분석하는 방법이다. 특정한 사항을 제한하여 분산 분석을 하는 것이다.^[1] 예를 들어, 교육 프로그램의 효과를 평가할 때, 학생들의 사전 지식을 공변량으로 통제하여 분석하는 경우가 이에 해당한다.

6. 추가 검사 (사후 검정)

분산 분석에서 통계적으로 유의미한 결과가 나타나면, 어떤 그룹이 다른 그룹과 유의미하게 다른지, 또는 다양한 가설을 검정하기 위해 추가적인 검정을 수행할 수 있다. 이러한 추가 검사를 사후 검정이라고 한다. 사후 검정은 데이터를 보기 전에 계획된 것인지, 아니면 데이터를 본 후에 고안된 것인지에 따라 구분된다.

사후 검정은 개별 그룹 평균을 비교하는 단순 비교일 수도 있고, 여러 그룹의 평균을 묶어서 비교하는 복합 비교일 수도 있다. 독립 변수가 정렬된 수준을 포함하는 경우, 선형이나 이차 관계와 같은 경향을 검사할 수도 있다. 사후 검정에는 다중 비교 문제를 조정하는 방법이 포함되는 경우가 많다.^[76]

특정 그룹, 변수, 요인 등이 통계적으로 다른 평균을 갖는지 확인하기 위한 사후 검정에는 투키 HSD, 던컨의 새로운 다중 범위 검정 등이 있다. 이러한 검정 결과는 비통계학적 청중에게 더 명확하게 전달하기 위해 간결 문자 디스플레이 (CLD) 방법론을 사용하기도 한다.^[76]

7. 활용 및 응용

분산 분석은 분리 가능한 부분으로 구성되며, 분산의 원천 분할 및 가설 검정을 개별적으로 사용할 수 있다. 분산 분석은 다른 통계 도구를 지원하는 데 사용된다. 회귀 분석은 먼저 데이터를 더 복잡한 모델에 적합시키는 데 사용된 다음, 분산 분석은 데이터를 적절하게 설명하는 간단한 모델을 선택하기 위해 모델을 비교하는 데 사용된다.^[42]

실험 설계에서는 요인의 변화가 반응에 통계적으로 유의미한 변화를 일으키는지 확인하기 위해 분산 분석이 활용된다. 실험은 반복적인 과정이므로, 한 실험의 결과는 다음 실험 계획을 변경하는 데 영향을 준다.

7. 1. 사회과학 분야

분산 분석은 여론 조사, 정책 효과 평가, 교육 프로그램 효과 분석 등 다양한 사회과학 연구에 활용된다. 그러나 무작위 실험이 아닌 관찰 연구에서 얻은 데이터에 적용될 때는 무작위화의 보증이 부족하여, '주관적인' 모델을 사용해야 한다.^[30] 관찰 연구에서 얻은 처치 효과 추정치는 일관성이 없는 경우가 많으므로, 통계 모델과 관찰 데이터는 신중하게 다루어야 할 가설을 제시하는 데 유용하다.^[31]

분산 분석은 여러 요인의 효과를 연구하는 것으로 일반화될 수 있다. 요인 실험은 각 요인의 모든 수준 조합에서 관측치가 포함될 때를 말하며, 일련의 단일 요인 실험보다 효율적이다.^[43] 여러 요인의 효과를 연구하기 위해 분산 분석을 사용할 때는 주 효과와 상호 작용 항에 대한 가설 검정이 필요하며, 상호 작용 항이 많아지면 거짓 양성이 발생할 위험이 증가한다. 다행히 경험에 따르면 고차 상호 작용은 드물다.^[44]

상호 작용을 감지하는 능력은 다중 요인 분산 분석의 주요 장점이지만, 상호 작용이 발생하면 주의해야 한다. 상호 작용 항을 먼저 테스트하고, 상호 작용이 발견되면 분산 분석 범위를 넘어서 분석을 확장해야 한다. 상호 작용은 실험 데이터의 해석을 복잡하게 만들기 때문에 유의성 계산이나 추정된 처리 효과를 액면 그대로 받아들일 수 없다.^[45] 이해를 돕기 위해 그래픽 방법을 사용하거나 회귀 분석을 활용하는 것이 좋다.

7. 2. 의학 분야

분산 분석은 의학 분야에서 신약의 효과를 검증하거나, 여러 치료 방법을 비교하고, 질병 발생 요인을 분석하는 등 다양한 연구에 활용된다.

7. 3. 공학 분야

분산 분석은 제품 품질 개선, 생산 공정 최적화, 신기술 효과 검증 등 다양한 연구에 활용된다. 분산 분석은 여러 요인의 효과를 연구하는 데 사용될 수 있으며, 이를 요인 실험이라고 한다. 요인 실험은 단일 요인 실험보다 효율적이며, 요인의 수가 증가함에 따라 효율성이 더욱 증가한다.^[43]

다중 요인 분산 분석에서는 상호 작용을 감지하는 것이 중요한 장점이다. 한 번에 하나의 요인만 테스트하면 상호 작용이 드러나지 않아 실험 결과가 일관성이 없어 보일 수 있다.^[43] 그러나 상호 작용이 발생하면 주의해야 한다. 상호 작용 항을 먼저 테스트하고, 상호 작용이 발견되면 분산 분석의 범위를 넘어서 분석을 확장해야 한다. 유의미한 상호 작용은 주 효과의 유의성을 가릴 수 있으므로,^[45] 이해를 돕기 위해 그래픽 방법을 사용하거나 회귀 분석을 활용하는 것이 좋다.

다중 요인 분산 분석에서는 비용 절감을 위해 반복을 최소화하거나, 효과가 통계적으로 유의하지 않은 경우 그룹을 결합하는 등의 기법을 사용할 수 있다.^[47]

8. 한계 및 주의점

분산 분석은 통계적 유의성 검정의 한 종류이다. 미국 심리학회를 비롯한 여러 단체에서는 통계적 유의성만을 보고하는 것은 부적절하며, 신뢰 구간을 함께 제시하는 것이 바람직하다는 견해를 갖고 있다.^[54]

균형 잡힌 실험(각 처리 조건에 동일한 수의 표본이 있는 실험)은 해석이 비교적 용이하지만, 불균형 실험(각 처리 조건에 표본 수가 다른 실험)은 더 복잡하다. 일원 분산 분석에서는 불균형 데이터에 대한 조정이 비교적 쉽지만, 불균형 분석은 강건성과 검정력이 모두 떨어진다.^[60] 더 복잡한 설계에서는 불균형으로 인해 문제가 더 복잡해진다. 균형 데이터에서는 주효과와 상호작용이 직교성을 갖지만, 불균형 데이터에서는 이러한 직교성이 나타나지 않아 일반적인 분산 분석 기법을 적용할 수 없다.^[61] 따라서 불균형 요인 분석은 균형 설계보다 훨씬 어렵다. 일반적으로 분산 분석은 불균형 데이터에도 적용할 수 있지만, 제곱합, 평균 제곱, F-비율은 변동 요인을 고려하는 순서에 따라 달라진다.^[42]

9. 관련 소프트웨어

SAS나 SPSS와 같은 주요 통계 패키지로 분산 분석을 실행할 수 있다. R 언어에도 분산 분석과 관련된 함수가 있다. 또한 분산 분석 및 그에 따른 다중 비교(multiple comparison)에 특화된 소프트웨어도 있으며, 대부분은 프리웨어이다.

js-STAR^[67]

: 다나카 사토시(신슈 대학) 교수가 제작한 "STAR"를 자바스크립트로 이식한 것이다. 3요인까지의 분산 분석, 단순 주효과 검정 및 다중 비교(LSD법, HSD법, Bonferroni법, Holm법)를 한 번에 수행할 수 있다. χ² 검정이나 상관계수 등도 다룰 수 있다. 웹상에서 바로 사용할 수 있으며, 다운로드도 가능하다. 인터페이스가 단순하고, 사용법도 알기 쉽다.

ANOVA4 on the Web^[68]

: 키리키 켄시 (히로시마 여학원 대학)가 제작하였다. 4요인까지의 분산 분석 및 다중 비교(Ryan법)가 한 번에 가능하다. 브라우저에서 바로 작동하며, 설치가 필요 없다.

분산 분석 프로그램 (AIST-ANOVA)^[69]

: 산업기술종합연구소 계측 표준 종합 센터 계측 표준 부문 물성 통계과 응용 통계 연구실에서 개발한, Excel의 애드인이다. 10요인까지의 분산 분석을 수행할 수 있다.

Excel NAG 통계 해석 애드인^[70]

: Excel에 분산 분석 함수를 추가하는 애드인이다. 아카데믹 버전, 무료 체험판도 있다.

ezANOVA^[71]

: 단독으로 동작하는 소프트웨어이므로 브라우저나 Excel을 필요로 하지 않는다.

MAANOVA^[72]

: MATLAB에서 분산 분석을 수행한다.

Origin

: Origin에서 분산 분석을 수행한다. 일원 배치/이원 배치, 반복이 있는 배치, Post-hoc 검정 등을 포함한다.

그 외에 범용 언어인 C 언어의 프로그램^[73], R 언어로 독자적으로 작성된 함수^[74] 등도 있다. 각 프로그래밍 언어를 사용할 수 있는 계산기 환경과 조작 능력이 필요하다.

참조

_[1] 논문 Stigler (1986)
_[2] 논문 Stigler (1986, p 134)
_[3] 논문 Stigler (1986, p 153)
_[4] 논문 Stigler (1986, pp 154–155)
_[5] 논문 Stigler (1986, pp 240–242)
_[6] 논문 Stigler (1986, Chapter 7 – Psychophysics as a Counterpoint)
_[7] 논문 Stigler (1986, p 253)
_[8] 논문 Stigler (1986, pp 314–315)
_[9] 간행물 The Correlation Between Relatives on the Supposition of Mendelian Inheritance Philosophical Transactions of the Royal Society of Edinburgh 1918
_[10] 논문 ) Studies in Crop Variation. I. An Examination of the Yield of Dressed Grain from Broadbalk
_[11] 논문 ) Studies in Crop Variation. II. The Manurial Response of Different Potato Varieties
_[12] 논문 Scheffé (1959, p 291, "Randomization models were first formulated by Neyman (1923) for the completely randomized design, by Neyman (1935) for randomized blocks, by Welch (1937) and Pitman (1937) for the Latin square under a certain null hypothesis, and by Kempthorne (1952, 1955) and Wilk (1955) for many other designs.")
_[13] 논문 Montgomery (2001, Chapter 12: Experiments with random factors)
_[14] 논문 Gelman (2005, pp. 20–21)
_[15] 서적 Statistical Methods
_[16] 논문 Cochran & Cox (1992, p 48)
_[17] 논문 Howell (2002, p 323)
_[18] 서적 Statistics for business and economics West Pub. Co
_[19] 논문 Anscombe (1948)
_[20] 서적 Design and Analysis of Experiments, Volume 2: Advanced Experimental Design https://books.google[...] John Wiley 2005
_[21] 서적 Planning of Experiments Wiley 1992
_[22] 문서 Unit-treatment additivity is simply termed additivity in most texts. Hinkelmann and Kempthorne add adjectives and distinguish between additivity in the strict and broad senses. This allows a detailed consideration of multiple error sources (treatment, state, selection, measurement and sampling) on page 161.
_[23] 논문 Kempthorne (1979, p 30)
_[24] 논문 Cox (1958, Chapter 2: Some Key Assumptions)
_[25] 논문 Hinkelmann and Kempthorne (2008, Volume 1, Throughout. Introduced in Section 2.3.3: Principles of experimental design; The linear model; Outline of a model)
_[26] 논문 Hinkelmann and Kempthorne (2008, Volume 1, Section 6.3: Completely Randomized Design; Derived Linear Model)
_[27] 논문 Hinkelmann and Kempthorne (2008, Volume 1, Section 6.6: Completely randomized design; Approximating the randomization test)
_[28] 논문 Bailey (2008, Chapter 2.14 "A More General Model" in Bailey, pp. 38–40)
_[29] 논문 Hinkelmann and Kempthorne (2008, Volume 1, Chapter 7: Comparison of Treatments)
_[30] 문서 Kempthorne (1979, pp 125–126, "The experimenter must decide which of the various causes that he feels will produce variations in his results must be controlled experimentally. Those causes that he does not control experimentally, because he is not cognizant of them, he must control by the device of randomization." "[O]nly when the treatments in the experiment are applied by the experimenter using the full randomization procedure is the chain of inductive inference sound. It is ''only'' under these circumstances that the experimenter can attribute whatever effects he observes to the treatment and the treatment only. Under these circumstances his conclusions are reliable in the statistical sense.")
_[31] 문서 Freedman {{full citation needed|date=November 2012}}
_[32] 논문 Montgomery (2001, Section 3.8: Discovering dispersion effects)
_[33] 논문 Hinkelmann and Kempthorne (2008, Volume 1, Section 6.10: Completely randomized design; Transformations)
_[34] 논문 Bailey (2008)
_[35] 논문 Montgomery (2001, Section 3-3: Experiments with a single factor: The analysis of variance; Analysis of the fixed effects model)
_[36] 서적 Cochran & Cox 1992
_[37] 서적 Cochran & Cox 1992
_[38] 서적 Hinkelmann and Kempthorne 2008
_[39] 서적 Rosenbaum 2002
_[40] 서적 Moore and McCabe 2003
_[41] 서적 Moore & McCabe 2003
_[42] 서적 Gelman 2008
_[43] 서적 Montgomery 2001
_[44] 서적 Belle 2008
_[45] 서적 Montgomery 2001
_[46] 서적 Cox 1958
_[47] 서적 Montgomery 2001
_[48] 서적 Wilkinson 1999
_[49] 서적 Montgomery 2001
_[50] 서적 Howell 2002
_[51] 서적 Howell 2002
_[52] 서적 Howell 2002
_[53] 서적 Moore and McCabe 2003
_[54] 서적 Wilkinson 1999
_[55] 서적 Montgomery 2001
_[56] 서적 Cochran & Cox 1957
_[57] 웹사이트 ANOVA Design https://bluebox.crei[...] 2023-01-23
_[58] 웹사이트 One-way/single factor ANOVA https://web.archive.[...]
_[59] 논문 The Probable Error of a Mean http://dml.cz/bitstr[...]
_[60] 서적 Montgomery 2001
_[61] 서적 Montgomery 2001
_[62] 서적 Gelman 2005
_[63] 서적 Montgomery 2001
_[64] 서적 Howell 2002
_[65] 서적 Howell 2002
_[66] 서적 Montgomery 2001
_[67] 웹사이트 js-STAR 2012 http://www.kisnet.or[...] 2012-04-04
_[68] 웹사이트 ANOVA4 on the Web http://www.hju.ac.jp[...] 2012-04-04
_[69] 웹사이트 不確かさWeb 分散分析プログラム http://www.nmij.jp/s[...] 2012-04-04
_[70] 웹사이트 Excel NAG 統計解析アドイン http://www.nag-j.co.[...] 2012-04-04
_[71] 웹사이트 ezANOVA free statistical software http://www.mccauslan[...] 2012-04-04
_[72] 웹사이트 maanova http://www.bioconduc[...] 2012-04-04
_[73] 웹사이트 ２因子多水準分散分析 http://web.sapmed.ac[...] 2012-04-04
_[74] 웹사이트 R Language http://web.sfc.keio.[...] 2012-04-04
_[75] 문서 "[[PSPP]], Univariate Analysis) Help-Reference Manual-GLM"
_[76] 문서 PSPP ,One-way ANOVA,Post-Hoc

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com