삼체 문제

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 수학적 기술
- 3.1. 제한 삼체 문제
4. 해의 성질
5. 천문학적 응용
6. 기타
참조

1. 개요

삼체 문제는 세 개의 질점을 가진 물체가 서로 중력의 영향을 받으며 움직이는 고전역학의 문제이다. 1687년 아이작 뉴턴에 의해 연구가 시작되었으며, 달의 운동 연구에 적용되었다. 1890년 앙리 푸앵카레는 일반해를 구하는 것이 불가능함을 증명했고, 20세기 초 칼 선드만은 해석적 해가 존재함을 증명했지만 실제 적용은 어려웠다.

수학적으로는 뉴턴 운동 방정식 또는 해밀턴 역학으로 표현되며, 에너지, 운동량, 각운동량 등이 보존된다. 일반 삼체 문제는 10개의 운동 적분이 존재하지만, 17개의 적분이 필요하므로 구적 가능하지 않다. 제한 삼체 문제는 세 번째 물체의 질량이 매우 작은 경우로, 두 물체의 운동은 케플러 운동으로 주어지고 세 번째 물체의 궤도를 구하는 문제로 단순화된다. 원형 제한 삼체 문제는 회전 좌표계를 사용하여 계산을 용이하게 한다.

삼체 문제는 특수해, 주기해, 적분 불가능성, 특이점, 최종 운동 등 다양한 해의 성질을 갖는다. 특수해로는 오일러와 라그랑주의 해가 있으며, 8자 궤도 해와 같은 주기해도 존재한다. 일반적인 폐쇄 형식 해는 존재하지 않으며, 슨드만의 급수는 실제 사용에 어려움이 있다. 특이점으로는 충돌 특이점과 비충돌 특이점이 있으며, 비충돌 특이점은 존재하지 않음이 증명되었다. 최종 운동은 쌍곡선-타원형 운동, 포물선 운동 등으로 분류된다.

천문학에서는 달의 운동 연구에 활용되었으며, 쌍성 형성에 기여한다. 또한 중력파 검출을 통해 이중 블랙홀 형성 시나리오의 중요한 요소로 검토되고 있다. 수치 적분을 통해 임의의 정밀도로 해결할 수 있으며, n체 문제의 특수한 경우이다. 헬륨 원자는 중력 삼체 문제의 양자역학적 유사체로 볼 수 있으며, 일반 상대성 이론을 사용하여 연구하기도 한다.

더 읽어볼만한 페이지

천체역학 - 공전
공전은 천문학에서 어떤 천체가 다른 천체의 중심 주위를 회전하는 운동을 의미하며, 태양계 행성, 위성, 은하 내 항성 등 다양한 천체에서 관찰되고, 케플러의 법칙에 따라 공전 주기가 결정된다.
천체역학 - 중력
중력은 질량을 가진 두 물체 사이에 작용하는 인력으로, 그 크기는 두 물체의 질량의 곱에 비례하고 거리의 제곱에 반비례하며, 지구에서는 물체를 아래로 떨어뜨리는 힘으로 작용하고, 일반 상대성 이론에서는 시공간의 곡률로 설명되며, 현대 물리학에서는 양자 중력 이론과 중력파 관측을 통해 연구되고 있다.
고전역학 - 천체역학
천체역학은 중력에 의해 지배되는 천체의 운동을 다루는 학문으로, 케플러 운동 법칙, 섭동 이론, 다체 문제 등을 포함하며, 뉴턴의 만유인력 법칙과 해석역학을 기반으로 발전하여 우주 탐사 및 행성 형성 연구에 기여한다.
고전역학 - 해밀토니언 (양자역학)
양자역학에서 해밀토니언은 계의 총 에너지를 나타내는 연산자로서, 고전역학의 해밀토니안에서 유래하며 슈뢰딩거 방정식을 통해 계의 시간적 진화를 결정하고, 그 고유값은 허용된 에너지 준위를 나타낸다.
물리학 개념 - 절연체
절연체는 전기 전도성을 막아 전기의 흐름을 제어하고 안전을 확보하며, 밴드 이론에 따라 큰 띠틈을 가져 외부 전압이 띠틈을 넘어서면 절연 파괴가 발생하며, 유리에서 세라믹, 고분자 복합 재료 등으로 제작되어 전선, 케이블 등 다양한 분야에 사용된다.
물리학 개념 - 전기 전도체
전기 전도체는 전기를 잘 통하는 물질로, 금속, 전해질, 초전도체, 반도체 등이 있으며, 구리, 은, 알루미늄 등 다양한 재료가 전선 등에 사용된다.

삼체 문제

2. 역사

아이작 뉴턴이 그의 저서 프린키피아에서 세 천체의 궤도에 대한 문제를 다루면서 삼체 문제가 시작되었다.^[27] 뉴턴은 중력을 주고받으며 움직이는 세 물체의 운동을 연구하고, 달 이론에 적용하여 달의 운동을 연구하는 첫 단계를 밟았다.^[29] 이후 이 문제는 다른 행성들과 지구 및 태양 간의 상호 작용에도 적용되었다.^[28]

장 르 롱 달랑베르와 알렉시 클레로는 삼체 문제에 대한 경쟁적인 분석 결과를 1747년에 프랑스 과학 아카데미에 제출했다.^[31] 1740년대 파리에서 그들의 연구와 관련하여 "삼체 문제"(Problème des trois Corps|프랑스어 발음^프랑스어)라는 이름이 일반적으로 사용되기 시작했으며, 1761년에 장 르 롱 달랑베르가 출판한 기록에 따르면 이 이름은 1747년에 처음 사용되었다고 한다.^[32] 피에르시몽 라플라스, 조제프루이 라그랑주 등도 삼체 문제를 연구하였다.

1890년에 앙리 푸앵카레는 삼체 문제의 일반해를 구하는 것은 불가능하다는 것을 증명하였는데,^[54] 이는 훗날 혼돈 이론의 모태가 되었다. 푸앵카레는 안정 다양체, 불안정 다양체가 교차하기 때문에 발생하는 호모클리닉 궤도라고 불리는 매우 복잡한 운동의 거동 개념에 도달했다.^[55]

칼 프리티오프 슨드만은 1912년에 삼체 문제에 대한 해석적 해가 존재함을 증명했지만,^[35] 이 해는 실제 적용이 어려웠다.

3. 수학적 기술

삼체 문제의 수학적 표현은 질량이 $m_i$ 인 세 물체의 위치 벡터 $\mathbf{r_i} = (x_i, y_i, z_i)$ 에 대한 뉴턴 운동 방정식으로 표현할 수 있다.^[3]

$\begin{align}\ddot\mathbf{r}_{\mathbf{1}} &= -G m_2 \frac{\mathbf{r_1} - \mathbf{r_2}}{|\mathbf{r_1} - \mathbf{r_2}|^3} - G m_3 \frac{\mathbf{r_1} - \mathbf{r_3}}{|\mathbf{r_1} - \mathbf{r_3}|^3}, \\\ddot\mathbf{r}_{\mathbf{2}} &= -G m_3 \frac{\mathbf{r_2} - \mathbf{r_3}}{|\mathbf{r_2} - \mathbf{r_3}|^3} - G m_1 \frac{\mathbf{r_2} - \mathbf{r_1}}{|\mathbf{r_2} - \mathbf{r_1}|^3}, \\\ddot\mathbf{r}_{\mathbf{3}} &= -G m_1 \frac{\mathbf{r_3} - \mathbf{r_1}}{|\mathbf{r_3} - \mathbf{r_1}|^3} - G m_2 \frac{\mathbf{r_3} - \mathbf{r_2}}{|\mathbf{r_3} - \mathbf{r_2}|^3}.\end{align}$

여기서 $G$ 는 중력 상수이다.

이 문제는 해밀턴 역학으로도 표현할 수 있는데, 이 경우 위치 $\mathbf{r_i}$ 및 운동량 $\mathbf{p_i}$ 의 각 구성 요소에 대해 18개의 1차 미분 방정식 집합으로 설명된다.

$\frac{d \mathbf{r_i}}{dt} = \frac{\partial \mathcal{H}}{\partial \mathbf{p_i}}, \qquad \frac{d\mathbf{p_i}}{dt} = -\frac{\partial \mathcal{H}}{\partial \mathbf{r_i}},$

여기서 $\mathcal{H}$ 는 해밀토니안이다.

$\mathcal{H} = -\frac{G m_1 m_2}$

-\frac{G m_2 m_3}

-\frac{G m_3 m_1}

+ \frac{\mathbf{p_1}^2}{2m_1} + \frac{\mathbf{p_2}^2}{2m_2} + \frac{\mathbf{p_3}^2}{2m_3}.

이 경우

\mathcal{H}

는 단순히 중력과 운동 에너지를 합한 시스템의 총 에너지이다.

제

i = 1, 2, 3

번째 물체의 운동 방정식은, 그 위치 벡터를

\boldsymbol{r}_i (t)

, 질량을

m_i

, 시간을

t

, 중력 상수를

G

로 할 때, 다음 식으로 주어진다.^[56]^[57]

:

m_i \frac{ d^2 \boldsymbol{r}_i }{ d t^2 } = - \sum_{j \neq i} G m_i m_j \frac{ \boldsymbol{r}_i - \boldsymbol{r}_j }{ | \boldsymbol{r}_i - \boldsymbol{r}_j |^3 }

일반 삼체 문제는, 이 3개의 연립미분 방정식을 풀어, 벡터 함수

\boldsymbol{r}_1 (t)

,

\boldsymbol{r}_2 (t)

,

\boldsymbol{r}_3 (t)

를 구하는 문제이다.

이 계에는 다음과 같은 10개의 운동 적분(오일러 적분)이 존재한다.^[58]

에너지 $E = \sum_i \frac{ 1 }{ 2 } m_i \boldsymbol{v}_i^2 - \frac{ 1 }{ 2 } \sum_{i \neq j} G \frac{ m_i m_j }{ | \boldsymbol{r}_i - \boldsymbol{r}_j | }$
운동량 벡터 $\boldsymbol{P} = \sum_i m_i \boldsymbol{v}_i$
각운동량 벡터 $\boldsymbol{L} = \sum_i m_i \boldsymbol{r}_i \times \boldsymbol{v}_i$
질량 중심 위치 벡터 $\boldsymbol{G} = \sum_i m_i \boldsymbol{r}_i - \boldsymbol{P} t$

이 계의 자유도는 18이므로, 삼체 문제가 구적 가능하기 위해서는 총 17개의 적분이 필요하지만, 이 외의 운동 적분은 존재하지 않으며, 적분의 수가 7개 부족하다. 따라서 삼체 문제는 구적 가능하지 않다.

삼체 문제의 해는 라그랑주 점과 같은 예외를 제외하고는 주로 섭동론이나 N체 시뮬레이션 등을 이용하여 산출된다.

3. 1. 제한 삼체 문제

셋째 물체의 질량이 첫 번째 물체 및 두 번째 물체의 질량에 비해 충분히 작을 때(

m_3 \ll m_1, m_2

) 첫 번째 물체 및 두 번째 물체의 운동 방정식에서 셋째 물체에 의한 중력의 기여를 무시할 수 있다. 이 근사 하에서의 삼체 문제를 특히 '''제한 삼체 문제'''라고 부른다.

제한 삼체 문제에서는 첫 번째 물체 및 두 번째 물체의 운동은 케플러 운동이며, 구할 수 있다. 따라서 이 경우, 두 물체가 만드는 중력장 내에서 운동하는 셋째 물체의 궤도를 구하는 것이 주된 문제가 된다.^[53]

:

\frac{ d^2 \boldsymbol{r} }{ d t^2 } = - \sum_{j = 1, 2} G m_j \frac{ \boldsymbol{r} - \boldsymbol{r}_j ( t ) }{ | \boldsymbol{r} - \boldsymbol{r}_j ( t ) | }

대부분의 경우 제한 삼체 문제 중 두 물체가 타원 궤도를 그리는 상황이 관심의 대상이 된다. 특히 그 궤도가 원 궤도 (이심률

e = 0

)인 경우를 circular restricted three-body problem|원 제한 삼체 문제^영어라고 부른다. 이 경우 공동 회전 좌표계에서는 첫 번째 몸체 및 두 번째 몸체가 정지하여 수학적인 취급이 용이해지므로, 공동 회전 좌표계를 사용하여 계산하는 경우가 많다. 이 좌표계에서 원 제한 삼체 문제의 운동 방정식은 원심력과 코리올리력을 포함하는 다음 형태를 취한다.^[53]

:

\ddot{x} = n^2 x + 2 n \dot{y} - G m_1 \frac{ x + a_1 }{ | \boldsymbol{r} + a_1 \hat{\textbf{x}} |^3 } - G m_2 \frac{ x - a_2 }{ | \boldsymbol{r} - a_2 \hat{\textbf{x}} |^2 }

:

\ddot{y} = n^2 y - 2 n \dot{x} - G m_1 \frac{ y }{ | \boldsymbol{r} + a_1 \hat{\textbf{x}} |^3 } - G m_2 \frac{ y }{ | \boldsymbol{r} - a_2 \hat{\textbf{x}} |^2 }

:

\ddot{z} = - G m_1 \frac{ z }{ | \boldsymbol{r} + a_1 \hat{\textbf{x}} |^3 } - G m_2 \frac{ z }{ | \boldsymbol{r} - a_2 \hat{\textbf{x}} |^2 }

여기서

a

를 두 물체 운동의 궤도 장반경으로 하여

a_1 = \frac{ m_2 }{ m_1 + m_2 } a

,

a_2 = \frac{ m_1 }{ m_1 + m_2 } a

이며, 첫 번째 몸체는 좌표

( - a_1, 0, 0 )

에, 두 번째 몸체는 좌표

( a_2, 0, 0 )

에 있는 것으로 했다. 또한

\hat{\textbf{x}}

는

x

축 단위 벡터이다. 원 제한 삼체 문제에는 야코비 적분으로 알려진 보존량

:

C_\mathrm{J} = \frac{ 2 G m_1 }{ | \boldsymbol{r} + a_1 \hat{\textbf{x}} | } + \frac{ 2 G m_2 }{ | \boldsymbol{r} - a_2 \hat{\textbf{x}} | } + n^2 ( x^2 + y^2 ) - ( \dot{x}^2 + \dot{y}^2 + \dot{z}^2 )

가 존재한다.^[53]

또한 첫 번째 몸체 또는 두 번째 몸체의 근방에는 그 천체의 중력이 강한 영향력을 가지고 있는, 지배적인 영역이 존재하며, 힐 권이라고 불린다.^[59]

4. 해의 성질

두 개의 질점이 서로 뉴턴 중력을 미치며 운동할 때, 그 궤도는 타원, 포물선, 쌍곡선 중 하나가 된다(케플러의 법칙). 삼체 문제는 이 계에 또 하나의 질점이 더해진 경우의 진화를 구하는 것으로, 태양-지구-달계나 태양-목성-토성계 등, 천체 역학의 다양한 국면에서 필요하기 때문에 오래 전부터 연구되어 왔다.

삼체 문제를 간단하게 만들기 위해 몇 가지 가정을 사용하기도 한다. 삼체 모두 동일 평면상에서 운동한다고 가정하는 '''평면 삼체 문제''', 삼체 중 하나의 질량이 다른 두 체에 영향을 미치지 않을 정도로 작다고 가정하는 '''제한 삼체 문제'''가 있다. 특히 제한 삼체 문제에서 나머지 두 체의 궤도를 원 궤도로 가정하는 경우를 '''원 제한 삼체 문제'''라고 부른다.

원 제한 삼체 문제에서의 라그랑주 점이나, 삼체의 질량이 같은 경우 8자형 궤도를 그리는 8자형 해^[53] 등이 특수 해로 알려져 있다.

삼체 문제가 구적 가능한가에 대한 적분 가능성에 대한 부정적인 결과는 프랑스의 수학자 앙리 푸앵카레에 의해 도출되었다.^[54] 푸앵카레는 제한 삼체 문제를 고찰하여, 운동을 결정하는 제1 적분이 일종의 섭동 급수로는 표현될 수 없다는 것을 보였다 (푸앵카레 정리). 또한, 안정 다양체, 불안정 다양체가 교차하기 때문에 발생하는 호모클리닉 궤도라는 매우 복잡한 운동의 거동 개념에 도달했다.^[55]

이러한 연구는 카오스 현상 연구와 현대적인 역학계 이론 발전의 계기가 되었다.

4. 1. 특수해

레온하르트 오일러는 1767년에 세 물체가 매 순간 공선상(일직선상)에 놓이는 세 가지 종류의 주기 해를 발견했다.^[53] 1772년에는 조제프루이 라그랑주가 세 물체가 매 순간 정삼각형을 이루는 해를 발견했다.^[60] 오일러의 공선 해와 라그랑주의 정삼각형 해는 삼체 문제의 중심 배치를 형성하며, 질량비에 관계없이 유효하고 물체들은 케플러 궤도를 따라 움직인다. 이 네 가지 종류의 해는 명시적인 해석 공식을 갖는 유일하게 알려진 해이다. 원형 제한 삼체 문제의 특수한 경우, 이 해들은 주 물체와 함께 회전하는 좌표계에서 라그랑주 점으로 불리는 점이 되며, L₁, L₂, L₃, L₄, L₅로 표시된다. 이 중 L₁, L₂, L₃는 세 물체가 일직선상에 놓이는 오일러의 직선 해이고, L₄와 L₅는 라그랑주의 해의 대칭적인 예이다.^[61]

원 제한 삼체 문제에서, 공전 회전계에서 제3체가 정지할 수 있는 5개의 점을 라그랑주 점이라고 부른다.

1993년, 산타페 연구소의 물리학자 크리스 무어는 세 개의 동일한 질량이 8자 모양으로 움직이는 각운동량 영점 해를 발견했다.^[15] 2000년, 수학자 알랭 솅시너와 리처드 몽고메리는 그 형식적 존재를 증명했다.^[16]^[17] 이 해는 질량 및 궤도 매개변수의 작은 섭동에 대해 수치적으로 안정적인 것으로 나타났지만, 안정성 영역이 좁아 실제로 관측될 가능성은 낮다고 주장되어 왔다.^[18]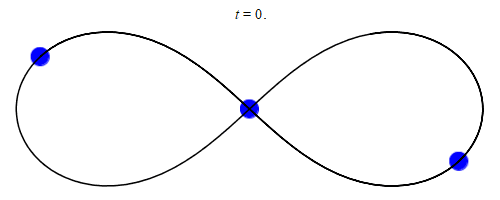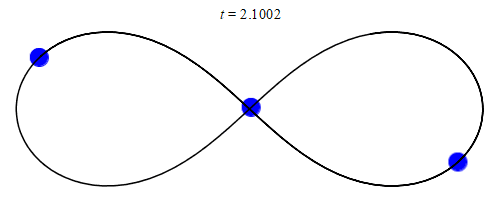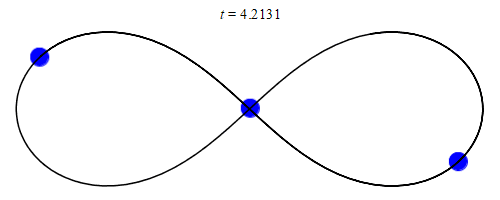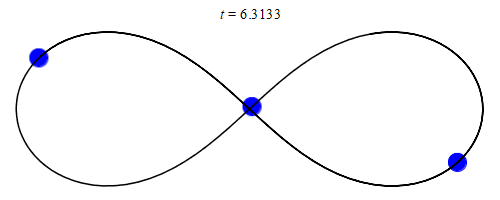

삼체 문제의 8자 궤도 해의 한 주기 T ≃ 6.3259에 대한 애니메이션

^[13]

2013년, 베오그라드 물리학 연구소의 물리학자 밀로반 슈바코프와 벨코 드미트라시노비치는 동일 질량, 각운동량 영점 삼체 문제에 대한 13개의 새로운 해 집합을 발견했다.^[8]^[14]

4. 2. 주기해

앙리 푸앵카레는 제한 삼체 문제에 무한히 많은 주기해(일정 시간 후 초기 상태로 돌아오는 해)가 존재함을 증명했다.^[66]^[67] 푸앵카레는 이러한 주기해가 난공불락으로 여겨졌던 문제에 접근할 수 있는 유일한 돌파구라고 비유했다.

컴퓨터 시대에 들어서면서 다양한 주기해를 수치적으로 계산하는 것이 가능해졌다. 1963년 리처드 아렌스토프는 제한 삼체 문제의 주기해인 Arenstorf orbit을 수치적으로 계산했다.^[70] 1967년 Szebehely 등은 피타고라스 삼체 문제 연구를 통해 주기해를 수치적으로 구성했다.^[71] 1970년대에는 미셸 에농 등에 의해 Broucke-Hadjidemetriou-Hénon family로 알려진 주기해 족이 발견되었다.^[72]^[73]^[74]^[75]^[76]^[77]^[78]^[79]

1990년대에는 세 물체가 하나의 닫힌 곡선 위를 움직이는 해(예: 8자 모양의 "8자 해")가 증명되어 주목받았다.^[80]^[81]^[82] 이 해는 카를레스 시모에 의해 n-body choreography|춤 해^영어로 명명되었으며, 유사한 방법을 통해 n체 문제의 주기해도 다수 얻어졌다.^[83]

4. 3. 적분 불가능성

앙리 푸앵카레는 삼체 문제가 구적 가능한지에 대한 적분 가능성에 대한 부정적인 결과를 도출했다.^[54] 1889년 스웨덴 겸 노르웨이 국왕 오스카르 2세의 환갑을 축하하기 위해 개최된 콘테스트에서, 푸앵카레는 몇 가지 가정을 둔 제한 삼체 문제를 고찰하여, 운동을 결정하는 제1 적분이 일종의 섭동 급수로는 표현될 수 없다는 것을 보였다 (푸앵카레 정리).^[54] 또한 푸앵카레는 이 연구 과정에서 안정 다양체, 불안정 다양체가 교차하기 때문에 발생하는 호모클리닉 궤도라고 불리는 매우 복잡한 운동의 거동 개념에 도달했다.^[55]

이러한 삼체 문제를 시초로 하는 적분 가능성 및 카오스 현상의 연구는 현대적인 역학계 이론의 발전에 계기가 되었다.

삼체 문제에 대한 일반적인 폐쇄 형식 해는 존재하지 않는다.^[1] 즉, 유한한 수의 표준 수학적 연산으로 표현될 수 있는 일반적인 해가 없다. 또한, 특별한 경우를 제외하고는 세 물체의 움직임은 일반적으로 반복되지 않는다.^[8]

4. 4. 특이점

n체 문제에서 유한 시간 $t \in [0, t^* )$ 내의 해 $( r_1 ( t ), r_2 ( t ), r_3 ( t ) )$를 시간 $t = t^* < \infty$ 이후로 연장할 수 없을 때, 그 점을 특이점(singularity)이라 부른다.^[93] 극한 $t \to t^*$에서 입자 좌표가 유한한 값으로 수렴하면, 이는 입자 간 충돌을 의미하므로^[92] 충돌 특이점(collision singularity)이라고 한다. 반면, 좌표가 유한값으로 수렴하지 않는 경우를 비충돌 특이점(non-collision singularity)이라 부른다.^[93] 하지만, 삼체 문제에서는 폴 팡르베가 비충돌 특이점이 존재하지 않음을 증명하였다(이 연구는 팡르베 추측의 시발점이 되었다).^[93]

툴리오 레비-치비타와 카를 순드만은 20세기 초 연구를 통해 삼체 문제에서 이체 충돌은 정칙 특이점이며, 적절한 좌표 변환을 통해 제거할 수 있음을 보였다.^[94]^[95]^[96]^[97] (자세한 내용은 레비-치비타 변환 참조). 반면, 삼체 동시 충돌은 지겔(1941)에 의해 진성 특이점이며, 정칙화될 수 없음이 밝혀졌다.^[98] 순드만은 삼체 충돌이 일어나려면 계의 총 각운동량이 0이어야 함을 증명하였다.^[99] (카를 바이어슈트라스는 순드만보다 먼저 이 사실을 알았으나, 증명을 발표하지는 않았다.^[100]) 또한, 순드만은 이 결과를 바탕으로 총 각운동량이 0이 아닌 초기 조건에 대해 모든 시간 $t$에서 수렴하는 삼체 문제의 무한 급수 해를 실제로 구성하여 그 존재를 증명하였다.^[101]^[102] 그러나 이 무한 급수 해는 수렴 속도가 매우 느려, 이 해로부터 유의미한 결론을 도출하는 것은 현실적으로 불가능하다.^[103]

1974년, McGehee는 현재 McGehee 변환이라 불리는 좌표 변환을 고안하고, 삼체 충돌 부근의 거동을 다루는 블로우 업(blow up) 기법을 개발하였다.^[104] 이 방법은 이후 연구에서 자주 활용되고 있다.^[108]

4. 5. 최종 운동

Chazy (1922)는^[106] 삼체 문제의 특이점이 없는 해가 시간이 무한대로 흐를 때 (

t \to \infty

) 다음 7가지 패턴 중 하나를 따른다고 결론지었다.^[107]

두 물체 간 거리가 모두 무한대로 발산하는 경우 ( $r_j \to \infty$ ( $j = 1, 2, 3$ )). 이 경우, 극한 $r_j / t \to C_j$ 가 존재하며, 그 값에 따라 다음 세 가지 패턴으로 분류된다.
쌍곡선 운동 (The hyperbolic motions) $H$ : $C_j > 0$ ( $j = 1, 2, 3$ ).
쌍곡선-포물선 운동 (The hyperbolic-parabolic motions) $HP_i$ : $C_i = 0$ 및 $C_j > 0$ ( $j \neq i$ ).
포물선 운동 (The parabolic motions) $P$ : $C_j = 0$ ( $j = 1, 2, 3$ ).
한 쌍의 두 물체 간 거리가 유계 ( $\sup_{t > 0} \{ r_i ( t ) \} < \infty$ )이며, 나머지 두 물체 간 거리는 무한대로 발산하는 ( $r_j \to \infty$ ( $j \neq i$ )) 경우. 이 경우에도 극한 $r_j / t \to C_j$ 에 따라 다음 두 가지 패턴으로 분류된다.
쌍곡선-타원 운동 (The hyperbolic-elliptic motions) $HE_i$ : $C_j > 0$ ( $j \neq i$ ).
포물선-타원 운동 (The parabolic-elliptic motions) $PE_i$ : $C_j = 0$ ( $j \neq i$ ).
그 외의 두 가지 패턴.
유계 운동 (The bounded motions) $B$ : $\sup_{t > 0} \{ r_1 ( t ), r_2 ( t ), r_3 ( t ) \} < \infty$ .
진동 운동 (The oscillatory motions) $OS$ : $\varlimsup_{t \to \infty} \sup_j \{ r_j ( t ) \} = \infty$ 및 $\varliminf_{t \to \infty} \sup_j \{ r_j ( t ) \} < \infty$ .

이 중 진동 운동^[108]의 경우, Chazy는 이론적으로 가능성을 제시했지만, 실제로 삼체 문제에서 존재하는지는 불분명했다. 1960년 Sitnikov^[109]가 제한 삼체 문제(현재 시트니코프 문제로 알려진 배열)에서 진동 운동 해가 존재함을 증명했다.

5. 천문학적 응용

달의 운동은 주로 지구의 중력장에 의해 발생하지만, 태양의 중력 또한 무시할 수 없는 영향을 미친다. 달의 궤도에 대한 이론은 삼체 문제로 정식화되었으며, 그 운동을 정확하게 구하기 위해 알렉시스 클레로, 조지 윌리엄 힐, 샤를 외젠 들로네, 어니스트 윌리엄 브라운 등의 연구에 의해 발전했다.^[62]

항성계 역학에서 삼체 상호 작용은 쌍성 형성의 중요한 경로이며, 계 전체의 진화에 영향을 미친다.^[108] 근접 쌍성의 로슈 모델은 원 제한 삼체 문제에 기초한다.^[115]

2010년대 중력파 직접 검출은 Binary black hole|이중 블랙홀^영어의 실재를 증명했고, 그 기원 문제를 제기했다.^[116] 삼체 상호작용은 이중 블랙홀 형성 시나리오의 중요한 요소 중 하나로 검토되고 있다.^[117]^[118]

6. 기타

컴퓨터 수치 적분을 통해 삼체 문제를 임의의 정밀도로 해결할 수 있지만, 높은 정밀도를 위해서는 많은 CPU 시간이 필요하다.^[24] 랜덤 워크 이론을 사용하면 다양한 결과에 대한 확률을 계산할 수 있다.^[25]^[26]

삼체 문제는 n체 문제의 특수한 경우이다.^[48] n체 문제는 n개의 물체가 중력과 같은 물리적 힘에 의해 어떻게 움직이는지를 설명한다.

양자 역학에서 헬륨 원자는 중력 삼체 문제와 유사하게 역제곱 법칙 쿨롱 상호작용에 따라 헬륨 원자핵과 두 개의 전자가 상호작용하며, 정확하게 풀 수 없다.^[41]

일반 상대성 이론을 사용하여 삼체 문제를 연구할 수도 있다.^[47] 물리적으로 상대론적 처리는 블랙홀의 사건의 지평선 근처와 같이 매우 강한 중력장이 있는 시스템에서 필요하다. 그러나 상대론적 문제는 뉴턴 역학보다 훨씬 더 어렵고, 수치 상대성 이론의 정교한 수치 기법이 필요하다.

참조

_[1] 간행물 The Three-Body Problem Princeton University Press
_[2] 웹사이트 Historical Notes: Three-Body Problem http://www.wolframsc[...] 2017-07-19
_[3] 웹사이트 PHYS 7221 Special Lecture—The Three-Body Problem http://www.phys.lsu.[...] Published by self, and [[Louisiana State University|LSU]] Department of Physics an Astronomy 2006-10-11
_[4] 서적 Poincaré and the Three Body Problem American Mathematical Society
_[5] 문서 Barrow-Green, p. 8, op. cit.
_[6] 학술지 The Three-Body Problem https://www.scientif[...] 2019-08
_[7] 학술지 An introduction to the classical three-body problem: From periodic solutions to instabilities and chaos Springer
_[8] 학술지 Physicists Discover a Whopping 13 New Solutions to Three-Body Problem https://www.science.[...] 2013-03-08
_[9] 문서 Barrow-Green, J. (2010). The dramatic episode of Sundman, Historia Mathematica 37, pp. 164–203.
_[10] 학술지 Application pratique des méthodes de M. Sundman à un cas particulier du problème des trois corps
_[11] 학술지 Numerische Berechnung eines Spezialfalles des Dreikörperproblems https://zenodo.org/r[...] 1913
_[12] 학술지 Complete Solution of a General Problem of Three Bodies 1967
_[13] 문서 Here the gravitational constant ''G'' has been set to 1, and the initial conditions are '''r'''₁(0) = -'''r'''₃(0) = (-0.97000436, 0.24308753); '''r'''₂(0) = (0,0); '''v'''₁(0) = '''v'''₃(0) = (0.4662036850, 0.4323657300); '''v'''₂(0) = (-0.93240737, -0.86473146). The values are obtained from Chenciner & Montgomery (2000).
_[14] 웹사이트 Three-body Gallery http://suki.ipb.ac.r[...] 2015-08-12
_[15] 학술지 Braids in classical dynamics http://tuvalu.santaf[...]
_[16] 학술지 A remarkable periodic solution of the three-body problem in the case of equal masses
_[17] 학술지 A new solution to the three-body problem https://www.ams.org/[...]
_[18] 학술지 A new outcome of binary–binary scattering
_[19] 학술지 New periodic solutions to the three-body problem and gravitational waves http://www.scl.rs/th[...] 2015-10
_[20] 학술지 More than six hundreds new families of Newtonian periodic planar collisionless three-body orbits 2017-12
_[21] 학술지 The 1223 new periodic orbits of planar three-body problem with unequal mass and zero angular momentum 2018-08
_[22] 학술지 Collisionless periodic orbits in the free-fall three-body problem
_[23] 학술지 Three-body periodic collisionless equal-mass free-fall orbits revisited 2024
_[24] 웹사이트 3body simulator https://3body.hk/ 2022-11-17
_[25] 뉴스 A Centuries-Old Physics Mystery? Solved https://scitechdaily[...] SciTech 2021-10-06
_[26] 학술지 Analytical, Statistical Approximate Solution of Dissipative and Nondissipative Binary-Single Stellar Encounters https://journals.aps[...] 2021-07-23
_[27] 서적 Three Body Dynamics and Its Applications to Exoplanets https://books.google[...] Springer International Publishing 2017
_[28] 서적 The Three-body Problem from Pythagoras to Hawking https://books.google[...] Springer
_[29] 서적 Philosophiæ naturalis principia mathematica https://lbezone.hkus[...] G. & J. Innys 1726
_[30] 웹사이트 Amerigo Vespucci https://www.biograph[...] 2021-06-23
_[31] 문서 The 1747 memoirs of both parties can be read in the volume of ''Histoires'' (including ''Mémoires'') of the Académie Royale des Sciences for 1745 (belatedly published in Paris in 1749) (in French):\n\n: Clairaut: "On the System of the World, according to the principles of Universal Gravitation" (at pp. 329–364); and\n: d'Alembert: "General method for determining the orbits and the movements of all the planets, taking into account their mutual actions" (at pp. 365–390).The peculiar dating is explained by a note printed on page 390 of the "Memoirs" section: "Even though the preceding memoirs, of Messrs. Clairaut and d'Alembert, were only read during the course of 1747, it was judged appropriate to publish them in the volume for this year" (i.e. the volume otherwise dedicated to the proceedings of 1745, but published in 1749).
_[32] 문서 Jean le Rond d'Alembert, in a paper of 1761 reviewing the mathematical history of the problem, mentions that Euler had given a method for integrating a certain differential equation "in 1740 (seven years before there was question of the Problem of Three Bodies)": see d'Alembert, "Opuscules Mathématiques", vol. 2, Paris 1761, Quatorzième Mémoire ("Réflexions sur le Problème des trois Corps, avec de Nouvelles Tables de la Lune ...") pp. 329–312, at sec. VI, p. 245.
_[33] 학술지 Precise numerical results for limit cycles in the quantum three-body problem 2006-01
_[34] 문서 "Coplanar Motion of Two Planets, One Having a Zero Mass". Annals of Mathematics, Vol. III, pp. 65–73, 1887. https://babel.hathit[...]
_[35] 서적 Poincaré and the Three Body Problem http://oro.open.ac.u[...] American Mathematical Society 1996-10-29
_[36] 논문 Energy levels arising from resonant two-body forces in a three-body system 1970-12-21
_[37] 논문 On the periodic solutions of the three-body problem https://academic.oup[...] 2019-11-01
_[38] 논문 Newton versus the machine: Solving the chaotic three-body problem using deep neural networks 2020
_[39] 뉴스 We Just Got 12,000 New Solutions to The Infamous Three-Body Problem https://www.sciencea[...] 2023-09-23
_[40] 논문 Three-body periodic collisionless equal-mass free-fall orbits revisited 2024
_[41] 서적 Introduction to Quantum Mechanics (2nd ed.) Prentice Hall
_[42] 논문 Exactly soluble two-electron atomic model
_[43] 논문 Solution of a Three-Body Problem in One Dimension
_[44] 논문 Motion of three vortices https://aip.scitatio[...] 1979-03-01
_[45] 논문 Integrable and chaotic motions of four vortices 1980-08-18
_[46] 논문 The vortex dynamics analogue of the restricted three-body problem: advection in the field of three identical point vortices https://iopscience.i[...] 1997-03-21
_[47] 논문 The three-body problem
_[48] 문서 "The Solution of the ''n''-body Problem" http://www.math.uvic[...]
_[49] 사전
_[50] 문서 Chapter.XIII
_[51] 문서
_[52] 문서
_[53] 논문 A remarkable periodic solution of the three-body problem in the case of equal masses https://doi.org/10.2[...] Mathematics Department, Princeton University
_[54] 간행물 "Sur le probléme des trois corps et les équations de la dynamique,"
_[55] 서적 Les Méthodes Nouvelles de la Méchanique Celeste https://archive.org/[...] Gauthier-Villars, Paris
_[56] 문서 다체문제
_[57] 문서 초속도, 초기위치, 충돌, 우주속도, 탈출속도
_[58] 서적 천체역학강의 東京大学出版会 1988
_[59] 사전 힐반지름
_[60] 문서 Essai sur le problème des trois corps
_[61] 서적 Theory of Orbits: Volume 1: Integrable Systems and Non-perturbative Methods Springer 1996
_[62] 서적 An Introduction to Celestial Mechanics Cambridge University Press 2012
_[63] 서적 The Restricted Three-Body Problem and Holomorphic Curves Birkhäuser Basel 2018
_[64] 논문 Researches in the Lunar Theory 1878
_[65] 논문 On the part of the motion of the lunar perigee which is a function of the mean motions of the sun and moon https://projecteucli[...] 1886
_[66] 웹사이트 Poincar ́e and the Three-Body Problem http://www.bourbaphy[...] 2020-10-09
_[67] 웹사이트 Henri Poincaré - Les méthodes nouvelles de la mécanique céleste, Tome 1, 1892 https://fr.wikisourc[...] 2020-10-09
_[68] 논문 Evolution of the moment of inertia of three-body figure-eight choreography
_[69] 서적 Solving Ordinary Differential Equations I Nonstiff Problems Springer 1993
_[70] 논문 Periodic Solutions of the Restricted Three Body Problem Representing Analytic Continuations of Keplerian Elliptic Motions https://ntrs.nasa.go[...]
_[71] 논문 A new periodic solution of the problem of three bodies 1967
_[72] 논문 1974
_[73] 논문 1975
_[74] 논문 1975
_[75] 논문 1975
_[76] 논문 1975
_[77] 논문 1975
_[78] 논문 1976
_[79] 논문 1977
_[80] 논문 Braids in classical dynamics 1993
_[81] 논문 A Remarkable Periodic Solution of the Three-Body Problem in the Case of Equal Masses 2000
_[82] 논문 9 Simple Choreographic Motions of N Bodies: A Preliminary Study 2002
_[83] 웹사이트 アニメーション of 柴山允瑠のホームページ http://yang.amp.i.ky[...] 2020-10-09
_[84] 논문 Über die Integrale des Vielkörper-Problems 1887
_[85] 서적 天体力学講義東京大学出版会 1988
_[86] 논문 Mémoire sur les intégrales premières du probléme des n corps 1898
_[87] 서적 重点解説ハミルトン力学系 : 可積分系とKAM理論を中心にサイエンス社
_[88] 문서 Ziglin, S.L.: On involutive integrals of groups of linear symplectic transformations and natural mechanicalsystems with homogeneous potential. Funktsional. Anal. i Prilozhen.34(3), 26-36 (2000)
_[89] 논문 A note on the non-integrability of some Hamiltonian systems with a homogeneous potential https://www.intlpres[...] International Press of Boston
_[90] 논문 On the meromorphic non-integrability of some ''N''-body problems https://doi.org/10.3[...] American Institute of Mathematical Sciences
_[91] 논문 Non-integrability of the three-body problem 2011
_[92] 문서 Sigel & Moser, p. 25.
_[93] 논문 Painlevé’s Conjecture 1993
_[94] 논문 1903
_[95] 논문 1904
_[96] 논문 Sur la résolution qualitative du problème restreint des trois corps https://projecteucli[...] 1906
_[97] 논문 Sur la régularisation du problème des trois corps https://projecteucli[...] 1920
_[98] 논문 Der Dreierstoss 1941
_[99] 문서 Siegel & Moser, p. 26.
_[100] 서적 Poincaré and the Three-Body Problem American Mathematical Society 1997
_[101] 논문 Mémoire sur le problème des trois corps https://babel.hathit[...]
_[102] 서적 Collisions, rings , and other Newtonian N-body problems American Mathematical Society 2005
_[103] 논문 The solution of the n-body Problem http://www.math.uvic[...] 1996
_[104] 논문 Triple Collision in the Collinear Three-Body Problem 1974
_[105] 논문 Complete solution of a general problem of three bodies 1967
_[106] 논문 Sur l’allure du mouvement dans le problème des trois corps quand le temps croît indéfiniment http://www.numdam.or[...] 1922
_[107] 논문 Final motions in the three-body problem and symbolic dynamics
_[108] 서적 自由落下三体問題における衝突軌道、振動運動とカオス http://id.nii.ac.jp/[...] 総合研究大学院大学 1997-03
_[109] 논문 The existence of oscillatory motions in the three-body problems http://www.mathnet.r[...] 1960
_[110] 논문 Quasirandom Dynamical Systems. I. Quasirandom Diffeomorphisms 1968
_[111] 논문 Quasirandom Dynamical Systems. II. One-Dimensional Nonlinear Oscillations in a Field with Periodic Perturbation 1968
_[112] 논문 Quasirandom Dynamical Systems. III Quasirandom Oscillations of One-Dimensional Oscillators 1969
_[113] 논문 The existence of oscillatory and superhyperbolic motion in Newtonian systems 1989
_[114] 논문 Arnold Diffusion and Oscillatory Solutions in the Planar Three-Body Problem 1994
_[115] 간행물 ロッシュモデル
_[116] 논문 The Origin of Binary Black Hole Mergers 2020
_[117] 웹사이트 Lecture notes onblack hole binary astrophysics https://arxiv.org/pd[...] 2018
_[118] 논문 Primordial black holes—perspectives in gravitational wave astronomy 2018

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com