쌍극자

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 분류
- 2.1. 전기 쌍극자
- 2.2. 자기 쌍극자
3. 분자 쌍극자
4. 양자역학적 쌍극자 연산자
5. 원자 쌍극자
6. 정적 자기 쌍극자의 장
- 6.1. 크기
- 6.2. 벡터 형태
7. 전기 쌍극자의 장
8. 쌍극자에 작용하는 토크
9. 쌍극자 복사
10. 활용 분야
참조

1. 개요

쌍극자는 크기가 같고 부호가 반대인 두 개의 점전하로 구성된 물리적 쌍극자에서 시작하여, 전하 또는 전류의 모든 구성이 갖는 '쌍극자 모멘트'를 포괄하는 개념이다. 쌍극자는 전기 쌍극자와 자기 쌍극자로 분류되며, 분자 수준에서는 영구, 순간, 유도 쌍극자로 나뉜다. 쌍극자는 전기장과 자기장을 생성하며, 특히 원거리에서의 장 계산에 중요한 역할을 한다. 양자역학적 연산자를 통해 표현되며, 원자 및 분자의 특성을 이해하는 데 사용된다. 쌍극자는 전자기학, 아마추어 무선, 기상학, 원자핵물리학, 음향학 등 다양한 분야에서 활용된다.

더 읽어볼만한 페이지

퍼텐셜 이론 - 푸아송 방정식
푸아송 방정식은 라플라스 연산자를 포함하는 2차 편미분 방정식으로, 전자기학 및 유체역학 등에서 계를 설명하고, 그린 함수나 수치적인 방법으로 해를 구할 수 있다.
퍼텐셜 이론 - 조화 함수
조화 함수는 유클리드 공간에서 정의되고 라플라스 연산자가 0이 되는 2차 연속 미분 가능한 함수로, 정칙 함수의 실해석적 대응물이며, 평균값 정리, 최대치 원리 등의 성질을 갖는다.
전자기학 - 전력
전력은 전압과 전류의 곱으로 계산되며, 발전소에서 생산되어 송전 및 배전을 통해 소비자에게 공급되고, 에너지 저장 기술을 통해 안정적으로 공급될 수 있으며, 산업, 상업, 가정 등 다양한 분야에서 소비된다.
전자기학 - 절연체
절연체는 전기 전도성을 막아 전기의 흐름을 제어하고 안전을 확보하며, 밴드 이론에 따라 큰 띠틈을 가져 외부 전압이 띠틈을 넘어서면 절연 파괴가 발생하며, 유리에서 세라믹, 고분자 복합 재료 등으로 제작되어 전선, 케이블 등 다양한 분야에 사용된다.

쌍극자
전자기학
정의	전기 쌍극자는 크기가 같고 부호가 반대인 두 전하가 분리되어 있는 것. 자기 쌍극자는 크기와 방향이 같은 닫힌 회로에 흐르는 전류
발생 원인	전하의 불균형 또는 전류 루프
전기 쌍극자 모멘트
정의	전기 쌍극자의 세기를 나타내는 벡터량. 음전하에서 양전하를 향하는 방향을 가짐
기호	p
단위	쿨롬 미터 (C·m)
공식	p = qd (q는 전하량, d는 음전하에서 양전하를 향하는 변위 벡터)
자기 쌍극자 모멘트
정의	자기 쌍극자의 세기를 나타내는 벡터량. 전류 루프의 면에 수직인 방향을 가짐
기호	m 또는 μ
단위	암페어 제곱미터 (A·m²) 또는 줄/테슬라 (J/T)
공식	m = IA (I는 전류, A는 전류 루프의 면적 벡터)
응용
분자 분극	분자 내의 전하 분포가 불균형하여 전기 쌍극자 모멘트를 가짐
자성 물질	원자 또는 분자가 자기 쌍극자 모멘트를 가짐
안테나	전파를 방출하거나 수신하는 장치로, 전기 쌍극자 또는 자기 쌍극자 모멘트를 이용
MRI	자기 쌍극자 모멘트를 가진 원자핵의 자기적 성질을 이용하여 인체 내부를 영상화
다중극 전개
설명	전하 또는 전류 분포에 의한 전위 또는 자기장을 쌍극자, 사중극자 등의 다중극 모멘트의 합으로 나타내는 방법
유용성	복잡한 전하 또는 전류 분포에 의한 장을 근사적으로 계산하거나 분석하는 데 유용

2. 분류

물리적 쌍극자는 두 개의 등가점 전하와 반대점 전하로 구성된다. 먼 거리(극의 분리에 비해 큰 거리)에서의 자기장은 위에서 정의한 쌍극자 모멘트에 거의 전적으로 의존한다. 점(전기) 쌍극자는 쌍극자 모멘트를 고정시킨 상태에서 거리가 0이 되도록 함으로써 얻어지는 극한이다. 점 쌍극자의 장은 특히 단순한 형태를 가지며, 다중극 전개에서 1차 항은 정확히 점 쌍극자장이다.

자연계에 알려진 자기 단극은 없지만, 전자와 같은 입자와 관련된 양자역학적 스핀 형태의 자기 쌍극자가 있다. 이론적인 자기 점 쌍극자는 전기 점 쌍극자의 전기장과 정확히 같은 형태의 자기장을 가지고 있다. 이러한 루프의 자기 쌍극자 모멘트는 루프를 흐르는 전류와 루프의 벡터 영역의 곱이다.

전하 또는 전류의 모든 구성은 '쌍극자 모멘트'를 가지며, 이는 주어진 구성의 장에 가장 가까운 장인 쌍극자를 기술한다. 이것은 총 전하("단극 모멘트")가 0일 때 다중극 전개의 한 항일 뿐이며, 자기 단극자가 없기 때문에 항상 자기 경우와 마찬가지이다. 쌍극자 항은 먼 거리를 계산할 때 영향을 가장 많이 주는 지배적인 항이다. 그 장은 다음 항(사극자)에 대해 및 더 높은 항에 대해 의 더 높은 거듭제곱 또는 단극자 항에 대해 에 비해 에 비례하여 떨어진다.

2. 1. 전기 쌍극자

물리적 쌍극자는 크기가 같고 부호가 반대인 두 개의 점전하로 구성된다. 먼 거리(즉, 극의 분리 거리보다 훨씬 큰 거리)에서의 장은 위에서 정의한 쌍극자 모멘트에 거의 전적으로 의존한다. 점(전기) 쌍극자는 쌍극자 모멘트를 고정한 상태에서 분리 거리를 0으로 접근시켜 얻은 극한이다. 점 쌍극자의 장은 특히 간단한 형태를 가지며, 다극 전개의 1차 항은 바로 점 쌍극자 장이다.^[5]

자연계에는 알려진 자기 단극이 없지만, 전자와 같은 입자와 관련된 양자 역학적 스핀 형태의 자기 쌍극자는 존재한다. 이론적인 자기 점 쌍극자는 전기 점 쌍극자의 전기장과 정확히 같은 형태의 자기장을 갖는다. 매우 작은 전류가 흐르는 고리는 근사적으로 자기 점 쌍극자이며, 이러한 고리의 자기 쌍극자 모멘트는 고리에 흐르는 전류와 고리의 (벡터) 면적의 곱이다.

전하 또는 전류의 임의 구성은 '쌍극자 모멘트'를 가지며, 이는 먼 거리에서 주어진 구성의 장을 가장 잘 근사하는 쌍극자를 설명한다. 이것은 총 전하("단극 모멘트")가 0일 때 다극 전개의 한 항일 뿐이다. 자기 경우에는 자기 단극이 없기 때문에 항상 그렇다. 쌍극자 항은 먼 거리에서 지배적인 항이다. 그 장은 에 비례하여 감소하는 반면, 다음 항인 사극 항은 이며, 더 높은 항은 의 더 높은 거듭제곱, 또는 단극 항은 이다.

원점에 있는 전기 쌍극자에 의한 위치 '''r'''에서의 정전 퍼텐셜은 다음과 같이 주어진다.

:

\Phi(\mathbf{r}) = \frac{1}{4\pi\epsilon_0}\,\frac{\mathbf{p}\cdot\hat{\mathbf{r}}}{r^2}

여기서 '''p'''는 (벡터) 쌍극자 모멘트이고, ''є''₀는 진공 유전율이다.

이 항은 임의의 정전 퍼텐셜 Φ('''r''')의 다중극 전개에서 두 번째 항으로 나타난다. 여기서 가정한 것처럼 Φ('''r''')의 원천이 쌍극자인 경우, 이 항은 Φ('''r''')의 다중극 전개에서 유일하게 0이 아닌 항이다. 쌍극자의 전기장은 이 퍼텐셜의 기울기에서 구할 수 있다.

:

\mathbf{E} = - \nabla \Phi =\frac {1} {4\pi\epsilon_0} \ \frac{3(\mathbf{p}\cdot\hat{\mathbf{r}})\hat{\mathbf{r}}-\mathbf{p}}{r^3} - \delta^3(\mathbf{r})\frac{\mathbf{p}}{3\epsilon_0}.

이는 점 자기 쌍극자의 자기장 표현과 같은 형태이며, 델타 함수는 무시한다.

그러나 실제 전기 쌍극자에서 전하는 물리적으로 분리되어 있으며, 전기장은 점전하에서 발산하거나 수렴한다. 이는 모든 곳에서 연속적인 실제 자기 쌍극자의 자기장과 다르다. 델타 함수는 점전하 사이의 반대 방향으로 향하는 강한 장을 나타내며, 쌍극자의 위치에서 장에 대한 관심이 거의 없기 때문에 종종 생략된다.^[10]

2. 2. 자기 쌍극자

물리적 쌍극자는 크기가 같고 부호가 반대인 두 개의 점전하로 구성된다. 먼 거리(극의 분리 거리에 비해 큰 거리)에서 자기장은 쌍극자 모멘트에 거의 전적으로 의존한다. 점(전기) 쌍극자는 쌍극자 모멘트를 고정한 상태에서 거리가 0이 되도록 함으로써 얻어지는 극한이다. 점 쌍극자의 장은 특히 단순한 형태를 가지며, 다중극 전개에서 1차 항은 정확히 점 쌍극자장이다.

자연계에 알려진 자기 단극은 없지만, 전자와 같은 입자와 관련된 양자역학적 스핀 형태의 자기 쌍극자가 있다. 이론적인 자기 점 쌍극자는 전기 점 쌍극자의 전기장과 정확히 같은 형태의 자기장을 가지고 있다. 매우 작은 전류 고리는 근사적으로 자기 점 쌍극자이며, 이러한 고리의 자기 쌍극자 모멘트는 고리를 흐르는 전류와 고리의 (벡터) 면적의 곱이다.

전하 또는 전류의 모든 구성은 '쌍극자 모멘트'를 가지며, 이는 주어진 구성의 장에 가장 가까운 장인 쌍극자를 기술한다. 이것은 총 전하("단극 모멘트")가 0일 때 다중극 전개의 한 항일 뿐이다. 자기 단극자가 없기 때문에 자기장의 경우 항상 이와 같다.

쌍극자 항은 먼 거리를 계산할 때 영향을 가장 많이 주는 지배적인 항이다. 그 장은 다음 항인 사극자 항에 대해 , 더 높은 항에 대해 의 더 높은 거듭제곱, 단극자 항에 대해 에 비해 에 비례하여 감소한다.

전자기학에서 단극자가 자하인 경우의 쌍극자를 자기 쌍극자라고 한다.

3. 분자 쌍극자

많은 분자는 다양한 원자에 대해 양전하와 음전하의 불균일한 분포로 인해 쌍극자 모멘트를 갖는다. 플루오르화수소(HF)와 같은 극성 화합물의 경우처럼, 전자 밀도가 원자들 사이에 불균등하게 공유되는 경우가 그렇다. 따라서 분자의 쌍극자는 고유한 전기장을 가진 전기 쌍극자이며, 자기장을 생성하는 자기 쌍극자와 혼동해서는 안 된다.

물리화학자인 피터 요세푸스 빌헬무스 데바이는 최초로 분자 쌍극자를 광범위하게 연구한 과학자였으며, 그 결과 쌍극자 모멘트는 그의 업적을 기리기 위해 ''데바이''라는 비SI 단위로 측정된다.

분자에는 영구 쌍극자, 순간 쌍극자, 유도 쌍극자의 세 가지 유형이 있다.

3. 1. 영구 쌍극자

분자 내에서 두 원자가 서로 다른 전기 음성도를 가질 때 영구 쌍극자가 발생한다. 전기 음성도가 큰 원자는 전자를 더 많이 끌어당겨 상대적으로 더 큰 음전하를 띠게 되고, 다른 원자는 양전하를 띠게 된다. 이러한 영구 쌍극자 모멘트를 가진 분자를 ''극성'' 분자라고 하며, 쌍극자-쌍극자 인력을 통해 상호작용한다.^[7]

유전율 측정을 통해 쌍극자 모멘트 값을 얻을 수 있으며, 몇 가지 일반적인 기체 상 분자의 쌍극자 모멘트 값 (단위: 데바이)은 다음과 같다.^[7]

물질	쌍극자 모멘트 (D)
이산화탄소	0
일산화탄소	0.112
오존	0.53
포스겐	1.17
암모니아	1.42
수증기	1.85
시안화수소	2.98
시아나마이드	4.27
브롬화칼륨	10.41

선형 분자인 이산화탄소(CO₂)는 두 결합 쌍극자가 상쇄되어 쌍극자가 0이다.

굽은 분자인 물(H₂O)은 순 쌍극자를 갖는다. 두 결합 쌍극자가 상쇄되지 않는다.

분자의 전체 쌍극자 모멘트는 개별 결합 쌍극자 모멘트들의 벡터 합으로 근사할 수 있다. 벡터 합은 결합의 상대적인 방향에 따라 달라지므로, 쌍극자 모멘트로부터 분자 기하학에 대한 정보를 얻을 수 있다.

예를 들어, 이산화탄소(CO₂)는 쌍극자 모멘트가 0인데, 이는 두 C=O 결합 쌍극자 모멘트가 서로 상쇄되어 분자가 선형임을 의미한다. 반면, 물(H₂O)은 굽은 구조를 가지므로 O-H 결합 모멘트가 상쇄되지 않아 쌍극자 모멘트를 가진다. 오존(O₃) 역시 굽은 분자이며, O-O 결합이 같은 원자 사이의 결합임에도 불구하고 결합 쌍극자 모멘트가 0이 아니다.

1,2-디클로로에텐의 ''시스'' 및 ''트랜스'' 이성질체는 쌍극자 모멘트를 통해 분자 구조를 예측할 수 있는 좋은 예시이다. ''시스'' 이성질체는 두 극성 C-Cl 결합이 C=C 이중 결합의 같은 쪽에 위치하여 1.90 D의 쌍극자 모멘트를 갖는다. 반면, ''트랜스'' 이성질체는 두 C-Cl 결합이 C=C 이중 결합의 반대쪽에 위치하여 쌍극자 모멘트가 상쇄되어 0이 된다.

삼불화붕소는 세 개의 극성 결합을 가지고 있지만, 붕소 양이온을 중심으로 플루오르화물 이온이 정삼각형으로 배치되어 대칭을 이루기 때문에 쌍극자 모멘트가 0이다.

3. 2. 순간 쌍극자

전자가 분자 내에서 다른 곳보다 한 곳에 더 집중되어 일시적인 쌍극자를 생성할 때 우연히 발생한다. 이러한 쌍극자는 영구 쌍극자보다 크기가 작지만, 그 빈도 때문에 화학과 생화학에서 여전히 중요한 역할을 한다. 런던 분산력 참조.

3. 3. 유도 쌍극자

유도 쌍극자는 영구 쌍극자를 가진 한 분자가 다른 분자의 전자를 밀어내어 그 분자에 쌍극자 모멘트를 *유도*할 때 발생할 수 있다. 유도 쌍극자를 띠는 분자는 *극성화된* 상태이다. 유도 쌍극자 인력을 참조하라.^[7]

보다 일반적으로, *어떤* 편극 가능한 전하 분포 ''ρ''(분자는 전하 분포를 갖는다는 것을 기억해야 한다)의 유도 쌍극자는 ''ρ'' 외부의 전기장에 의해 발생한다. 이 전기장은 ''ρ'' 근처의 이온이나 극성 분자에서 유래하거나 거시적일 수 있다(예: 대전된 축전기 판 사이의 분자). 유도 쌍극자 모멘트의 크기는 외부 장의 세기와 ''ρ''의 쌍극자 편극률의 곱과 같다.^[7]

4. 양자역학적 쌍극자 연산자

전하 ''q_i''^영어와 위치 벡터 '''r'''_''i''^영어를 갖는 ''N''개의 입자 집합을 생각할 수 있다. 예를 들어, 이 집합은 모두 전하 −''e''를 갖는 전자와 전하 ''eZ_i''를 갖는 원자핵으로 구성된 분자일 수 있다. 여기서 ''Z_i''는 ''i''번째 원자핵의 원자 번호이다.

쌍극자 측정값(물리량)은 양자역학적 '''쌍극자 연산자'''를 갖는다.

: $\mathfrak{p} = \sum_{i=1}^N \, q_i \, \mathbf{r}_i \, .$

이 정의는 중성 원자 또는 분자, 즉 총 전하가 0인 경우에만 유효하다. 이온화된 경우에는 다음과 같다.

: $\mathfrak{p} = \sum_{i=1}^N \, q_i \, (\mathbf{r}_i - \mathbf{r}_c) ,$

여기서 $\mathbf{r}_c$ 는 분자/입자 집합의 질량 중심이다.^[8]

5. 원자 쌍극자

비축퇴(S-상태) 원자는 영구 쌍극자 모멘트가 0일 수밖에 없다. 이 사실은 원자의 반전 대칭성으로부터 양자역학적으로 유도된다. 쌍극자 연산자의 세 성분 모두 핵에 대한 반전에 대해 반대칭이다.

: $\mathfrak{I} \;\mathfrak{p}\; \mathfrak{I}^{-1} = -\mathfrak{p},$

여기서 $\mathfrak{p}$ 는 쌍극자 연산자이고 $\mathfrak{I}$ 는 반전 연산자이다.

비축퇴 상태(축퇴 준위 참조)에 있는 원자의 영구 쌍극자 모멘트는 쌍극자 연산자의 기댓값(평균값)으로 주어진다.

: $\left\langle \mathfrak{p} \right\rangle = \left\langle\, S\, | \mathfrak{p} |\, S \,\right\rangle,$

여기서 $|\, S\, \rangle$ 는 S-상태의 비축퇴 파동함수이며, 반전에 대해 대칭 또는 반대칭이다: $\mathfrak{I}\, |\, S\, \rangle = \pm|\, S\, \rangle$ . 켓(ket) 안의 파동함수와 브라(bra) 안의 그 복소 켤레의 곱은 항상 반전 및 그 역변환에 대해 대칭이므로,

: $\left\langle \mathfrak{p} \right\rangle =\left\langle\, \mathfrak{I}^{-1}\, S\, | \mathfrak{p} |\, \mathfrak{I}^{-1}\, S\, \right\rangle =\left\langle\, S\, | \mathfrak{I}\, \mathfrak{p}\, \mathfrak{I}^{-1} |\, S\, \right\rangle =$

\left\langle \mathfrak{p} \right\rangle

기댓값은 반전에 따라 부호가 바뀐다. 여기서

\mathfrak{I}

가 대칭 연산자이므로 유니터리임을 사용했다:

\mathfrak{I}^{-1} =  \mathfrak{I}^{*}\,

그리고 정의에 의해 에르미트 수반

\mathfrak{I}^*\,

는 브라에서 켓으로 옮길 수 있으며, 그러면

\mathfrak{I}^{**} = \mathfrak{I}\,

가 된다. 자신과 같은 값의 음수인 유일한 양은 0이므로, 기댓값은 사라진다.

:

\left\langle \mathfrak{p} \right\rangle = 0.

열린 껍질 원자의 경우 축퇴된 에너지 준위를 가지고 있을 때, 1차 슈타르크 효과를 이용하여 쌍극자 모멘트를 정의할 수 있다. 이것은 축퇴된 에너지에 속하는 파동함수 중 일부가 반대의 패리티를 갖는 경우에만(즉, 반전에 대해 다른 거동을 보이는 경우에만) 0이 아닌 쌍극자(정의에 따라 0이 아닌 1차 슈타르크 이동에 비례)를 제공한다. 이것은 드문 경우이지만, 2s 상태와 2p 상태가 "우연히" 축퇴되어(이 축퇴의 원인에 대해서는 라플라스-룬게-렌츠 벡터 문서 참조) 패리티가 반대인(2s는 짝수이고 2p는 홀수임) 들뜬 수소 원자의 경우 발생한다.

6. 정적 자기 쌍극자의 장

물리적 쌍극자는 두 개의 동일하지만 반대되는 점전하로 구성된다. 먼 거리에서 이 쌍극자의 자기장은 쌍극자 모멘트에 거의 전적으로 의존한다. 점(전기) 쌍극자는 쌍극자 모멘트를 고정한 상태에서 두 전하 사이의 거리가 0이 되도록 하는 극한으로 얻어진다. 점 쌍극자의 장은 매우 단순한 형태를 가지며, 다중극 전개에서 1차 항이 바로 점 쌍극자장이다.

자연계에는 자기 홀극이 존재하지 않지만, 전자와 같은 입자는 양자역학적 스핀 형태의 자기 쌍극자를 가진다. 이론적인 자기 점 쌍극자는 전기 점 쌍극자의 전기장과 정확히 같은 형태의 자기장을 가진다. 이러한 루프의 자기 쌍극자 모멘트는 루프를 흐르는 전류와 루프의 벡터 면적을 곱한 값이다.

전하나 전류의 모든 구성은 '쌍극자 모멘트'를 가지는데, 이는 주어진 구성의 장에 가장 가까운 장을 갖는 쌍극자를 나타낸다. 이는 총 전하("단극 모멘트")가 0일 때 다중극 전개의 한 항일 뿐이며, 자기 단극자가 없기 때문에 항상 자기장의 경우와 마찬가지이다.

쌍극자 항은 먼 거리에서 가장 큰 영향을 미치는 지배적인 항이다. 그 장은 다음 항인 사중극자 항에 대해 , 더 높은 항에 대해 , 단극자 항에 대해 에 비해 에 비례하여 감소한다.

6. 1. 크기

쌍극자 자기장의 원거리 세기 ''B''는 다음과 같이 주어진다.

:

B(m, r, \lambda) = \frac{\mu_0}{4\pi} \frac{m}{r^3} \sqrt{1 + 3\sin^2(\lambda)} \, ,

여기서 각 변수는 다음을 의미한다.

''B''는 자기장의 세기(단위: 테슬라)
''r''은 중심으로부터의 거리(단위: 미터)
''λ''는 자기 위도(90° − ''θ''와 같음). 여기서 ''θ''는 쌍극자 축으로부터의 자기 공동위도(단위: 라디안 또는 각도)^[9]
''m''은 쌍극자 모멘트(단위: 암페어 제곱미터 또는 줄/테슬라)
''μ''₀는 진공의 투자율(단위: 헨리/미터)

원통 좌표계로의 변환은

r^2 = z^2 + \rho^2

를 사용하여 이루어지며,

:

\lambda = \arcsin\left(\frac{z}{\sqrt{z^2 + \rho^2}}\right)

여기서 ''ρ''는 ''z''축으로부터의 수직 거리이다. 그러면,

:

B(\rho, z) = \frac{\mu_0 m}{4 \pi \left(z^2 + \rho^2\right)^\frac32} \sqrt{1 + \frac{3 z^2}{z^2 + \rho^2}}

6. 2. 벡터 형태

자기장은 벡터량이다.

:

\mathbf{B}(\mathbf{m}, \mathbf{r}) =\frac{\mu_0}{4\pi} \ \frac{3(\mathbf{m} \cdot \hat{\mathbf{r}}) \hat{\mathbf{r}} - \mathbf{m}}{r^3}

여기서

'''B'''는 자기장이다.
'''r'''은 쌍극자의 위치에서 자기장을 측정하는 위치까지의 벡터이다.
''r''은 '''r'''의 절댓값, 즉 쌍극자로부터의 거리이다.
은 '''r'''과 평행한 단위 벡터이다.
'''m'''은 (벡터) 쌍극자 모멘트이다.
''μ''₀는 진공의 투자율이다.

이것은 점쌍극자의 자기장과 정확히 일치하며, 임의의 자기장의 다중극 전개에서 쌍극자 항과 정확히 일치하고, 먼 거리에서는 어떤 쌍극자와 유사한 배열의 자기장을 근사적으로 나타낸다.

7. 전기 쌍극자의 장

물리적 쌍극자는 크기가 같고 부호가 반대인 두 개의 점전하로 구성된다. 먼 거리(극의 분리 거리에 비해 큰 거리)에서 쌍극자의 장은 쌍극자 모멘트에 거의 전적으로 의존한다. 점(전기) 쌍극자는 쌍극자 모멘트를 고정한 채 거리가 0이 되도록 하여 얻어지는 극한이다. 점 쌍극자의 장은 특히 단순한 형태를 가지며, 다중극 전개에서 1차 항은 정확히 점 쌍극자 장이다.

자연계에는 알려진 자기 단극이 없지만, 전자와 같은 입자와 관련된 양자 역학적 스핀 형태의 자기 쌍극자가 있다. 이론적인 자기 점 쌍극자는 전기 점 쌍극자의 전기장과 정확히 같은 형태의 자기장을 가지고 있다. 매우 작은 전류 고리는 근사적으로 자기 점 쌍극자이며, 이 고리의 자기 쌍극자 모멘트는 고리를 흐르는 전류와 고리의 (벡터) 면적의 곱이다.

전하 또는 전류의 구성은 '쌍극자 모멘트'를 가지며, 이는 주어진 구성의 장에 가장 가까운 장인 쌍극자를 기술한다. 이것은 총 전하("단극 모멘트")가 0일 때 다중극 전개의 한 항일 뿐이다. 자기 단극자가 없기 때문에 자기의 경우는 항상 그렇다.

쌍극자 항은 먼 거리를 계산할 때 영향을 가장 많이 주는 지배적인 항이다. 그 장은 다음 항(사중극자)에 대해 및 더 높은 항에 대해 의 더 높은 거듭제곱 또는 단극자 항에 대해 에 비해 에 비례하여 떨어진다.

원점에 있는 전기 쌍극자에 의한 위치 '''r'''에서의 정전 퍼텐셜은 다음과 같다.

: $\Phi(\mathbf{r}) = \frac{1}{4\pi\epsilon_0}\,\frac{\mathbf{p}\cdot\hat{\mathbf{r}}}{r^2}$

여기서 '''p'''는 (벡터) 쌍극자 모멘트이고, ''є''₀는 진공 유전율이다.

이 항은 임의의 정전 퍼텐셜 Φ('''r''')의 다중극 전개에서 두 번째 항으로 나타난다. 여기서 가정한 것처럼 Φ('''r''')의 원천이 쌍극자인 경우, 이 항은 Φ('''r''')의 다중극 전개에서 유일하게 0이 아닌 항이다. 쌍극자의 전기장은 이 퍼텐셜의 기울기에서 구할 수 있다.

: $\mathbf{E} = - \nabla \Phi =\frac {1} {4\pi\epsilon_0} \ \frac{3(\mathbf{p}\cdot\hat{\mathbf{r}})\hat{\mathbf{r}}-\mathbf{p}}{r^3} - \delta^3(\mathbf{r})\frac{\mathbf{p}}{3\epsilon_0}.$

이는 점 자기 쌍극자의 자기장 표현과 같은 형태이며, 델타 함수는 무시한다.

그러나 실제 전기 쌍극자에서 전하는 물리적으로 분리되어 있으며, 전기장은 점전하에서 발산하거나 수렴한다. 이는 모든 곳에서 연속적인 실제 자기 쌍극자의 자기장과 다르다. 델타 함수는 점전하 사이의 반대 방향으로 향하는 강한 장을 나타내며, 쌍극자의 위치에서 장에 대한 관심이 거의 없기 때문에 종종 생략된다.^[5]^[10]

8. 쌍극자에 작용하는 토크

균일한 전기장 또는 자기장에 놓인 쌍극자는 양쪽에 크기는 같지만 방향이 반대인 힘이 작용하여 토크를 생성한다.

전기 쌍극자 모멘트 '''p'''(쿨롱·미터 단위)의 경우 토크는 다음과 같다.

: $\boldsymbol{\tau} = \mathbf{p} \times \mathbf{E}$

자기 쌍극자 모멘트 '''m'''(암페어 제곱미터 단위)의 경우 토크는 다음과 같다.

: $\boldsymbol{\tau} = \mathbf{m} \times \mathbf{B}$

결과적으로 생성되는 토크는 쌍극자를 인가된 장에 정렬시키려는 경향이 있으며, 전기 쌍극자의 경우 다음과 같은 퍼텐셜 에너지를 생성한다.

: $U = -\mathbf{p} \cdot \mathbf{E}$

자기 쌍극자의 에너지는 다음과 같다.

: $U = -\mathbf{m} \cdot \mathbf{B}$

9. 쌍극자 복사

진동하는 전기 쌍극자에 대한 포인팅 벡터의 크기(정확한 해). 두 전하는 두 개의 작은 검은 점으로 표시됨.

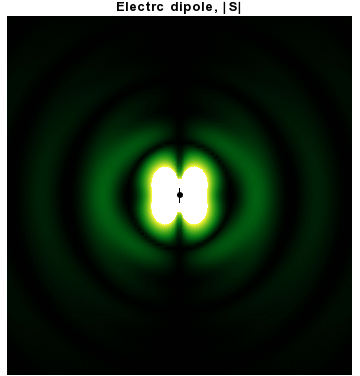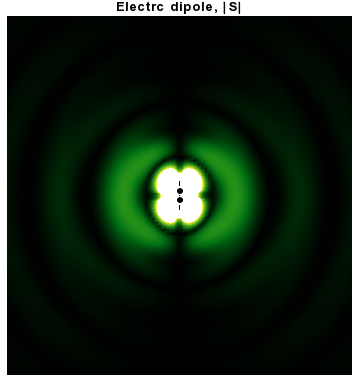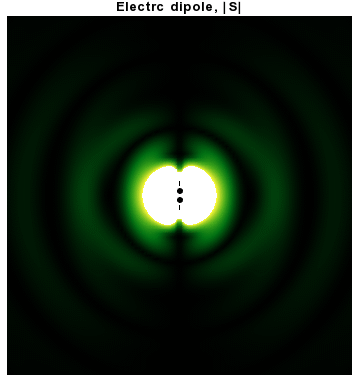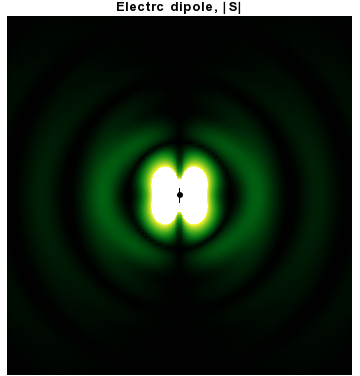
정전기의 쌍극자 외에도 시간에 따라 진동하는 전기 또는 자기 쌍극자를 고려하는 것이 일반적이다. 이것은 구면파 복사에 대한 확장이거나 더 물리적인 다음 단계이다.

특히, 각진동수 ''ω''와 '''ẑ''' 방향을 따라 ''p''₀인 쌍극자 모멘트를 갖는 조화적으로 진동하는 전기 쌍극자를 고려해 보자.

:

\mathbf{p}(\mathbf{r}, t) = \mathbf{p}(\mathbf{r})e^{-i\omega t} = p_0\hat{\mathbf{z}}e^{-i\omega t} .

진공 상태에서 이 진동하는 쌍극자에 의해 생성되는 정확한 장은 지체 포텐셜 공식을 사용하여 다음과 같이 유도할 수 있다.

:

\begin{align}\mathbf{E} &= \frac{1}{4\pi\varepsilon_0} \left\{\frac{\omega^2}{c^2 r} \left( \hat{\mathbf{r}} \times \mathbf{p} \right) \times \hat{\mathbf{r}} +\left( \frac{1}{r^3} - \frac{i\omega}{cr^2} \right)\left( 3\hat{\mathbf{r}} \left[\hat{\mathbf{r}} \cdot \mathbf{p}\right] - \mathbf{p} \right)\right\} e^\frac{i\omega r}{c} e^{-i\omega t} \\\mathbf{B} &= \frac{\omega^2}{4\pi\varepsilon_0 c^3} (\hat{\mathbf{r}} \times \mathbf{p}) \left( 1 - \frac{c}{i\omega r} \right) \frac{e^{i\omega r/c}}{r} e^{-i\omega t}.\end{align}

\frac{r\omega}{c} \gg 1

에 대해, 원거리장은 방사하는 "구면"파의 더 간단한 형태를 취하지만, 외적에 포함된 각 의존성을 갖는다.^[11]

:

\begin{align}\mathbf{B}&=  \frac{\omega^2}{4\pi\varepsilon_0 c^3} (\hat{\mathbf{r}} \times \mathbf{p}) \frac{e^{i\omega (r/c - t)}}{r}=  \frac{\omega^2 \mu_0 p_0 }{4\pi c} (\hat{\mathbf{r}} \times \hat{\mathbf{z}}) \frac{e^{i\omega (r/c - t)}}{r}= -\frac{\omega^2 \mu_0 p_0 }{4\pi c} \sin(\theta) \frac{e^{i\omega (r/c - t)}}{r} \mathbf{\hat{\phi}} \\\mathbf{E}&=  c \mathbf{B} \times \hat{\mathbf{r}}= -\frac{\omega^2 \mu_0 p_0}{4\pi} \sin(\theta) \left(\hat{\phi} \times \mathbf{\hat{r}}\right) \frac{e^{i\omega (r/c - t)}}{r}= -\frac{\omega^2 \mu_0 p_0}{4\pi} \sin(\theta) \frac{e^{i\omega (r/c - t)}}{r} \hat{\theta}.\end{align}

시간 평균 포인팅 벡터

:

\langle \mathbf{S} \rangle = \left(\frac{\mu_0 p_0^2\omega^4}{32\pi^2 c}\right) \frac{\sin^2(\theta)}{r^2} \mathbf{\hat{r}}

는 등방적으로 분포되지 않고 비구면 전기 및 자기파의 결과로 쌍극자 모멘트에 수직인 방향 주위에 집중된다. 사실, 이러한 토로이달 각 분포를 담당하는 구면 조화 함수(sin ''θ'')는 정확히 ''l'' = 1 "p"파이다.

장에 의해 방사되는 총 시간 평균 전력은 포인팅 벡터에서 다음과 같이 유도할 수 있다.

:

P = \frac{\mu_0 \omega^4 p_0^2}{12\pi c}.

전력의 주파수에 대한 4제곱 의존성은 레일리 산란과 하늘이 주로 파란색으로 구성되는 기본적인 효과와 일치한다.

원형 편광 쌍극자는 두 개의 선형 쌍극자의 중첩으로 설명된다.

10. 활용 분야

쌍극자는 여러 분야에서 활용되는 개념이다. 전자기학에서는 단극자가 전하인 경우의 쌍극자를 전기쌍극자라고 하며, 단극자가 자하인 경우의 쌍극자를 자기쌍극자라고 한다.

아마추어 무선의 다이폴 안테나, 기상학의 다이폴 모드 현상, 원자핵물리학의 거대 쌍극자 공명, 소프트 다이폴 모드 등에서도 이 개념이 사용된다. 음향학에서도 쌍극자 개념이 사용되며,^[14] 음원의 한 종류로 취급된다.

참조

_[1] 서적 A Greek-English Lexicon https://www.perseus.[...] Perseus
_[2] 서적 A Greek-English Lexicon https://www.perseus.[...] Perseus
_[3] 백과사전 dipole, n. Oxford University Press
_[4] 서적 Modern Problems in Classical Electrodynamics Oxford University Press
_[5] 서적 Introduction to Electrodynamics https://archive.org/[...] Prentice Hall
_[6] 서적 Introduction to Quantum Mechanics Prentice Hall
_[7] 서적 CRC Handbook of Chemistry and Physics CRC Press
_[8] 웹사이트 The Electric Dipole Moment Vector -- Direction, Magnitude, Meaning, et cetera http://www.av8n.com/[...]
_[9] 문서 Magnetic colatitude is 0 along the dipole's axis and 90° in the plane perpendicular to its axis.
_[10] 서적 Classical Electrodynamics, 3rd Ed. Wiley
_[11] 서적 Introduction to Electrodynamics Prentice Hall
_[12] 서적 학술용어집 물리학편 培風館
_[13] 서적 基礎音響学講談社サイエンティフィク
_[14] 서적 フーリエ音響学シュプリンガー・フェアラーク東京
_[15] 서적 Modern Problems in Classical Electrodynamics Oxford University Press
_[16] 서적 Introduction to Electrodynamics https://archive.org/[...] Prentice Hall
_[17] 서적 Introduction to Quantum Mechanics Prentice Hall
_[18] 서적 A Greek-English Lexicon https://www.perseus.[...] Perseus
_[19] 서적 A Greek-English Lexicon https://www.perseus.[...] Perseus
_[20] 백과사전 dipole, n. Oxford University Press

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com