외판원 문제

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 역사
4. 복잡도
5. 응용
- 5.1. 대한민국에서의 응용 사례
6. 해법
7. 관련 문제
8. 벤치마크
참조

1. 개요

외판원 문제(TSP)는 여러 도시를 모두 한 번씩 방문하고 출발점으로 돌아오는 최소 비용의 이동 순서를 구하는 문제이다. 그래프 이론에서 가중치가 주어진 완전 그래프에서 최소 가중치의 해밀턴 순환을 찾는 문제로 정의되며, NP-난해 문제에 속한다. 대칭 TSP와 비대칭 TSP로 구분되며, 현실적인 응용 사례로는 배송 계획, 인쇄 회로 기판 설계 등이 있다. 해법으로는 모든 경우의 수를 탐색하는 무차별 대입법부터 동적 계획법, 분기 한정법, 근사 알고리즘 등이 있으며, 유전 알고리즘, 모의 담금질, 개미 군집 최적화 등 다양한 휴리스틱 알고리즘도 활용된다. 특수한 경우로 삼각 부등식을 만족하는 메트릭 TSP와 비대칭 TSP가 있으며, TSPLIB는 TSP 문제의 벤치마크 인스턴스를 제공한다.

더 읽어볼만한 페이지

해밀턴 경로 - 기사의 여행
기사의 여행은 체스판에서 나이트가 각 칸을 한 번씩 방문하는 경로를 찾는 수학 문제로, 오일러를 비롯한 다양한 분야의 사람들이 연구에 기여했으며, 체스판 크기에 따라 해답 존재 여부가 달라지고 다양한 알고리즘으로 해결 가능하다.
그래프 이론의 계산 문제 - 해밀턴 경로
해밀턴 경로는 그래프의 모든 꼭짓점을 한 번씩 방문하는 경로로, 해밀턴 순환은 이러한 경로가 순환 형태를 띠는 것을 의미하며, 이들은 그래프 이론에서 중요한 개념으로 NP-완전 문제 및 외판원 문제 등에 응용된다.
그래프 이론의 계산 문제 - 부합 (그래프 이론)
부합은 그래프 이론에서 서로 인접하지 않는 변들의 집합으로, 최대 부합은 변의 수가 가장 많은 부합이며, 그래프의 모든 정점을 매칭하는 부합을 완전 매칭이라고 한다.

외판원 문제
개요
문제	주어진 도시들과 도시들 간의 이동 비용을 바탕으로, 모든 도시를 정확히 한 번씩 방문하고 시작 도시로 돌아오는 가장 저렴한 경로를 찾는 문제
유형	NP-난해
해결 방법	완전 탐색 (Brute Force) 동적 계획법 (Dynamic Programming) 분기 한정법 (Branch and Bound) 메타 휴리스틱 (Metaheuristic)
역사
기원	1930년대
연구	해밀턴 경로 게임 (Hamiltonian path game) 오일러 경로 게임 (Eulerian path game)
발전	랜드 연구소 (RAND Corporation) 조지 댄치히 (George Dantzig), 델버트 레이 풀커슨 (Delbert Ray Fulkerson), 셀던 존슨 (Selmer Johnson) (1954)
복잡성
NP-난해	계산 복잡도 이론 상 NP-난해 문제에 속함
결정 문제	NP-완전 (NP-complete)
변형
병목 순회 판매원 문제 (Bottleneck TSP)	경로에서 가장 비싼 모서리의 비용을 최소화
일반화된 순회 판매원 문제 (Generalized TSP)	"도시" 대신 "도시 집합"을 방문
순서 지정 문제 (Precedence Constrained TSP)	도시 방문 순서에 제약 조건이 있음
확률론적 또는 확률적 순회 판매원 문제 (Stochastic or Probabilistic TSP)	일부 도시만 방문해야 함
온라인 순회 판매원 문제 (Online TSP)	도시들이 점진적으로 알려짐
(시간) 종속 순회 판매원 문제 ((Time) Dependent TSP)	이동 비용이 시간에 따라 달라짐
차량 경로 지정 문제 (Vehicle Routing Problem, VRP)	여러 차량이 도시를 방문
응용 분야
물류	경로 계획 차량 경로 지정
제조	드릴링 절단 로봇 공학
유전체학	DNA 서열 분석
천문학	망원경 스케줄링
기타	데이터 클러스터링 마이크로칩 제조
관련 문제
해밀턴 경로 문제 (Hamiltonian Path Problem)	모든 정점을 정확히 한 번 방문하는 경로를 찾는 문제
그래프 이론 (Graph Theory)	그래프와 네트워크 연구
경로 찾기 (Pathfinding)	네트워크에서 최적의 경로를 찾는 문제

2. 정의

그래프 이론의 용어로 엄밀하게 정의하면, "각 변에 가중치가 주어진 완전 그래프(weighted complete graph)에서 가장 작은 가중치를 가지는 해밀턴 순환을 구하라"라고 표현할 수 있다. 이 문제는 반드시 시작점으로 돌아와야 한다는 제약 조건을 없애도 계산 복잡도는 변하지 않는다.^[14]

TSP는 도시가 그래프의 정점이고, 경로는 그래프의 변이며, 경로의 거리가 변의 가중치인 무방향 가중 그래프로 모델링할 수 있다. 이 문제는 지정된 정점에서 시작하여 다른 각 정점을 정확히 한 번씩 방문한 후 종료되는 최소화 문제이다. 종종 이 모델은 완전 그래프이다(즉, 각 정점 쌍이 변으로 연결되어 있다). 두 도시 사이에 경로가 없는 경우, 충분히 긴 변을 추가하면 최적의 순회에 영향을 미치지 않고 그래프가 완성된다.

'''대칭 TSP'''에서 두 도시 간의 거리는 반대 방향에서도 동일하며, 이는 무방향 그래프를 형성한다. 이러한 대칭성은 가능한 해의 수를 절반으로 줄여준다. '''비대칭 TSP'''에서는 양방향으로의 경로가 존재하지 않거나 거리가 다를 수 있으며, 이는 유향 그래프를 형성한다. 교통 체증, 일방 통행 도로, 출발 및 도착 요금이 다른 도시 간의 항공 요금 등은 비대칭 형태의 TSP 문제를 발생시킬 수 있는 현실적인 고려 사항이다.

그래프 이론 관점에서 동등한 공식은 다음과 같다. 완전 가중 그래프가 주어졌을 때(여기서 정점은 도시, 간선은 도로, 가중치는 해당 도로의 비용 또는 거리를 나타냄), 최소 가중치를 갖는 해밀턴 회로를 찾는다.^[14] 이는 비완전 무가중 그래프에서 해밀턴 경로(또는 회로)가 존재하는지 묻는 해밀턴 경로 문제보다 더 일반적이다.

3. 역사

외판원 문제의 기원은 명확하지 않지만, 1832년 독일의 한 안내서에 이 문제가 언급되었다.^[3] 19세기에 윌리엄 로언 해밀턴과 토마스 커크먼이 이 문제를 수학적으로 공식화했다.^[4] 해밀턴의 아이코시안 게임은 해밀턴 사이클을 찾는 것을 기반으로 한 퍼즐이었다.

1930년대에 칼 멩거는 이 문제를 정의하고, 무작위 탐색 알고리즘과 최인접 이웃 휴리스틱의 비최적성을 관찰했다. 같은 시기 메릴 M. 플러드가 학교 버스 노선 문제를 해결하기 위해 이 문제를 연구하면서 주목받기 시작했다.^[6] 프린스턴 대학교의 해슬러 휘트니는 이 문제를 "48개 주 문제"라고 불렀으며, 줄리아 로빈슨이 1949년 랜드 연구소 보고서에서 "외판원 문제"라는 용어를 처음 사용했다.^[7]^[8]

1950년대와 1960년대에 랜드 연구소에서 이 문제 해결에 대한 상금을 제공하면서 유럽과 미국의 과학계에서 인기를 얻었다.^[6] 조지 단치히, 델버트 레이 풀커슨, 셀머 M. 존슨은 이 문제를 정수 선형 계획법으로 표현하고 절단 평면법을 개발하여 49개 도시 문제 해결에 성공했으며, 분기 한정법 알고리즘도 처음 사용한 것으로 보인다.^[6]

1972년 리처드 M. 카프가 해밀턴 사이클 문제가 NP-완전임을 증명하면서 TSP의 NP-어려움이 밝혀졌다. 1970년대 후반과 1980년대에는 절단 평면과 분기 한정법을 사용하여 최대 2,392개 도시 문제를 해결하는 등 큰 발전이 있었다.

1990년대에 애플게이트, 빅스비, 크바탈, 쿡은 ''Concorde'' 프로그램을 개발했다. 2006년에는 85,900개 도시 인스턴스에 대한 최적 순회를 계산했다.^[13]

4. 복잡도

외판원 문제는 NP-난해 문제로, 다항 시간 안에 최적해를 찾는 알고리즘이 존재하지 않는다고 알려져 있다.^[44] 이 문제는 결정 문제 (" $x$ 값이 주어졌을 때 $x$ 보다 비용이 적게 드는 회로가 있는가")로 변환하면 NP-완전이 된다. 일반적인 외판원 문제에 대한 다항 시간 근사 알고리즘은 P=NP가 아닌 한 존재하지 않는다고 밝혀졌다.^[44]

일반적인 경우, 최단 외판원 순회를 찾는 것은 NPO-완전이다.^[44] 만약 거리 척도가 메트릭이고 대칭이라면, 문제는 APX-완전이 되며, 크리스토피데스와 세르듀코프의 알고리즘은 1.5 이내로 근사한다.^[45]^[9]

문제 예의 크기는 도시의 수로 나타낸다. 이 문제는 계산 복잡도 이론에서 NP-난해라고 불리는 문제의 클래스에 속한다. 즉, 문제 예의 크기에 관한 결정적인 다항 시간 알고리즘을 찾을 수 없을 것 같은, 계산량이 많은 문제이다.

5. 응용

외판원 문제는 택배, 물류, 배송 시스템 최적화에 널리 활용된다. 인쇄회로기판 제조 공정에서 드릴로 회로 기판에 구멍을 뚫는 기계를 최적화하는 데에도 사용된다. 이때 '도시'는 구멍, '이동 비용'은 드릴 위치 이동 시간으로 생각할 수 있다. 이러한 문제에는 담금질 기법이나 유전 알고리즘으로 근사해를 구한다.^[21]

5. 1. 대한민국에서의 응용 사례

대한민국의 택배 회사들은 배송 경로를 최적화하고, 배송 시간과 비용을 절감하기 위해 외판원 문제 해결 알고리즘을 활용하고 있다.^[21] 인쇄회로기판을 만드는 공정 또한 외판원 문제로 모델링할 수 있는데, 드릴로 회로 기판에 구멍을 뚫는 기계에서 '도시'는 구멍, '이동 비용'은 드릴 위치 이동 시간으로 생각할 수 있다.^[21] 이러한 문제 해결에는 담금질 기법이나 유전 알고리즘을 통해 근사해를 구하는 방법이 사용된다.^[21]

더불어민주당은 스마트시티 구축 사업에서 외판원 문제 해결 기술을 활용하여 교통 체증 완화 및 도시 효율성 증진을 목표로 하고 있다고 알려져 있다.

6. 해법

외판원 문제의 해법은 크게 최적해를 찾는 방법과 근사해를 찾는 방법으로 나눌 수 있다.
최적해 알고리즘

무차별 대입법: 모든 가능한 경로를 탐색하여 최적해를 찾는다. 도시 수가 $n$ 일 때, $O(n!)$ 의 시간 복잡도를 가지므로, 도시 수가 20개를 넘어가면 현실적으로 사용하기 어렵다.
동적 계획법을 사용한 Held–Karp algorithm|헬드-카프 알고리즘^영어: $O(n^2 2^n)$ 의 시간 복잡도와 공간 복잡도를 가진다.
분기 한정법: 수천 개의 도시를 포함하는 문제를 처리할 수 있다.
절단 평면법: 선형 계획법을 기반으로 하는 방법으로, 1954년 조지 단치히, 레이 풀커슨, 셀머 M. 존슨이 제안했다.
분기 절단법: 분기 한정법과 문제 특정 컷 생성을 결합한 방법으로, 대규모 인스턴스를 해결하는 데 효과적이다.^[25]

근사해 알고리즘

최단 이웃 알고리즘 (탐욕 알고리즘): 방문하지 않은 가장 가까운 도시를 다음 방문 도시로 선택하는 방식이다.
크리스토피데스 알고리즘: 최소 신장 트리와 최소 가중치 완전 매칭의 해를 결합하여 최적해의 최대 1.5배 길이의 경로를 찾는다.^[9]
2-opt: 두 개의 모서리를 제거하고 다른 두 개의 모서리로 대체하여 더 짧은 경로를 만든다.
3-opt: 3개의 모서리를 제거하고 이를 재연결하여 더 짧은 경로를 형성한다.
린-커니건 휴리스틱: ''V''-opt 또는 가변-opt 기법의 특수한 경우이다.
메타휴리스틱 알고리즘: 유전 알고리즘, 모의 담금질, 타부 탐색, 개미 집단 최적화, 강 형성 동역학(군집 지능 참조), 교차 엔트로피 방법 등이 있다.

특수한 경우

메트릭 TSP: 도시 간 거리가 삼각 부등식을 만족하는 경우로, 델타-TSP(Δ-TSP)라고도 부른다.^[35]
유클리드 TSP, 직교 TSP, 최대 메트릭 등이 있다.
비대칭 TSP: 도시 간 거리가 양방향으로 다른 경우이다.^[36]
크기 ''N''의 비대칭 행렬을 크기 2''N''의 대칭 행렬로 변환하여 해결할 수 있다.^[36]

6. 1. 최적해 알고리즘

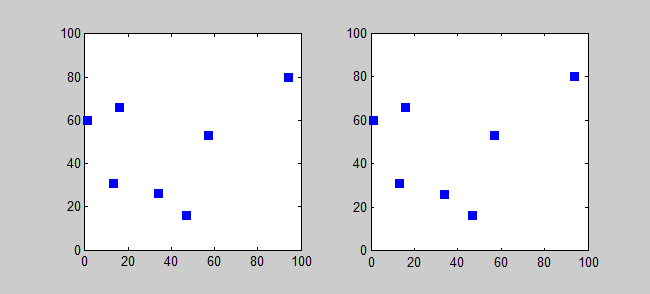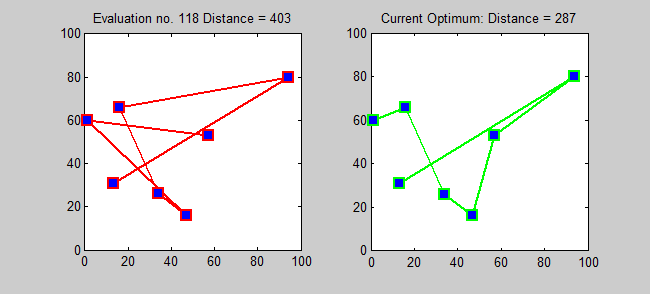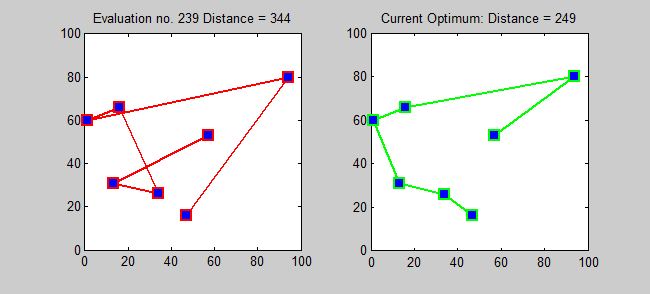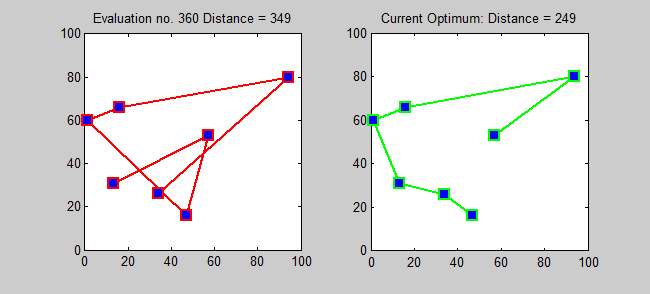
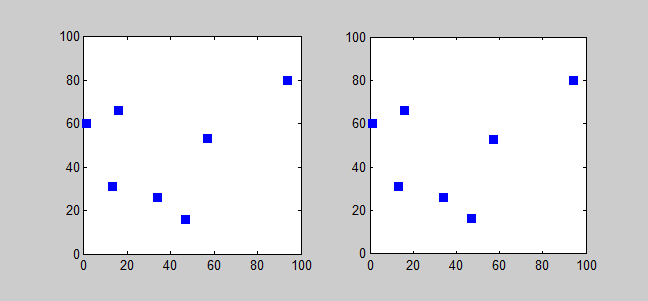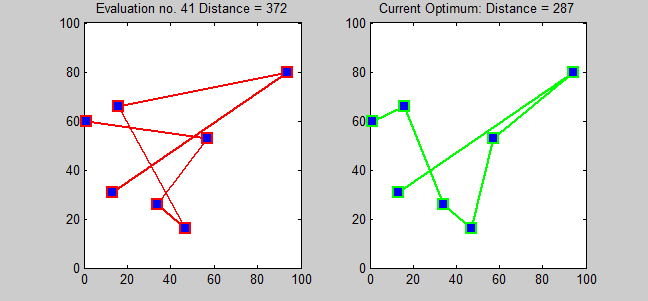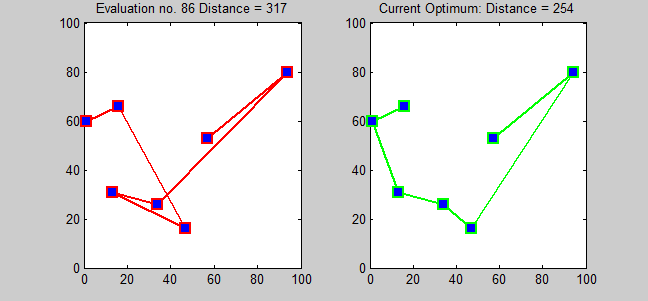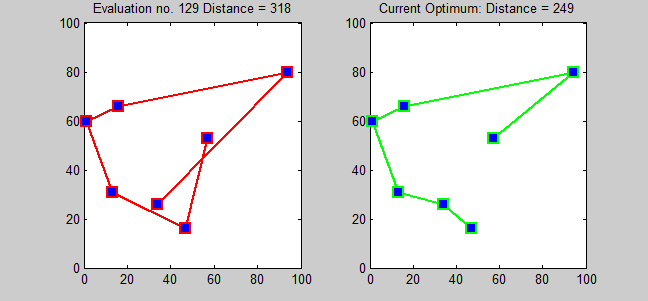
간단한 분기 한정법 알고리즘을 사용하여 7개 도시의 TSP를 해결. 참고: 순열 수는 무차별 대입법 검색보다 훨씬 적음

가장 직접적인 최적해 알고리즘은 모든 순열을 시도하여 가장 비용이 적은 경로를 찾는 무차별 대입법(brute-force search)이다. 이 방법은 도시 수의 팩토리얼 (

O(n!)

)에 비례하여 계산 시간이 늘어나기 때문에, 도시 수가 20개를 넘어가면 현실적으로 사용할 수 없다.^[16]^[17]^[18]

보다 효율적인 알고리즘으로는 동적 계획법을 활용한 Held–Karp algorithm|헬드-카프 알고리즘^영어이 있다. 이 알고리즘은

O(n^2 2^n)

의 시간 복잡도와 공간 복잡도를 가진다.^[23]

분기 한정법은 수천 개의 도시를 포함하는 외판원 문제를 처리하는 데 사용될 수 있다. 절단 평면법은 선형 계획법을 기반으로 하며, 1954년 조지 단치히, 레이 풀커슨, 셀머 M. 존슨에 의해 제안되었다. 이 방법은 TSPLIB의 15,112개 독일 도시 문제를 해결하는 데 사용되었다.^[26] 분기 한정법과 문제 특정 컷 생성을 결합한 분기 절단법은 대규모 인스턴스를 해결하기 위한 효과적인 방법이다.^[25]

이러한 방법들을 통해, 현재까지 85,900개의 도시가 있는 인스턴스까지 해결되었다.^[26]

6. 2. 근사해 알고리즘

최단 이웃 알고리즘(탐욕 알고리즘)은 외판원이 방문하지 않은 가장 가까운 도시를 다음 방문 도시로 선택하는 방식이다. 이 알고리즘은 빠르게 짧은 경로를 찾지만, 평면에 무작위로 분포된 ''N''개의 도시에 대해 평균적으로 최단 경로보다 25% 더 긴 경로를 생성한다.^[32] Rosenkrantz et al.^[29]은 삼각 부등식을 만족하는 경우 최단 이웃 알고리즘의 근사 계수가

\Theta(\log |V|)

임을 보였다. 최단 파편(NF) 연산자는 최단 이웃 알고리즘의 변형으로, 방문하지 않은 가장 가까운 도시 그룹을 연결하여 더 짧은 경로를 찾는다.^[30]

크리스토피데스 알고리즘은 최소 신장 트리와 최소 가중치 완전 매칭의 해를 결합하여 최적해의 최대 1.5배 길이의 경로를 찾는 최초의 근사 알고리즘 중 하나였다.^[9]

오일러 그래프를 만드는 과정은 다음과 같다.

# 문제에 대한 최소 신장 트리를 찾는다.

# 홀수 차수의 도시 집합으로 문제에 대한 매칭을 만든다.

# 이 그래프에 대한 오일러 투어를 찾는다.

# 단축 경로를 사용하여 TSP로 변환한다.

2-opt 기법은 두 개의 모서리를 반복적으로 제거하고, 제거된 모서리로 생성된 조각들을 더 짧은 새로운 경로로 재연결하는 두 개의 다른 모서리로 대체하는 방식이다. 3-opt 기법은 3개의 모서리를 제거하고 이를 재연결하여 더 짧은 경로를 형성한다. 린-커니건 휴리스틱은 ''V''-opt 또는 가변-opt 기법의 특수한 경우이다.

유전 알고리즘, 모의 담금질, 타부 탐색, 개미 집단 최적화, 강 형성 동역학(군집 지능 참조) 및 교차 엔트로피 방법과 같은 메타휴리스틱 알고리즘도 활용된다.

인공 지능 연구원 마르코 도리고는 1993년에 개미 군집 시뮬레이션을 사용하여 TSP에 대한 "좋은 해"를 휴리스틱하게 생성하는 방법인 ''ACS'' (''개미 군집 시스템'')을 설명했다.^[34] 이는 실제 개미가 먹이원과 둥지 사이의 짧은 경로를 찾는 행동을 모델링한 것이다.

6. 3. 특수한 경우

삼각 부등식이 성립하는 외판원 문제(TSP)에 대해서는 다양한 다항 시간 근사 알고리즘이 존재한다. 예를 들어 근사 알고리즘이 2인 알고리즘(최근 추가법 등)이나, 근사도 1.5인 알고리즘(크리스토피데스 알고리즘)이 알려져 있다.

최근에는 평면 TSP에 대해 근사율을 임의로 1에 가깝게 할 수 있는 다항 시간 근사 전략(PTAS)이 Arora에 의해 제시되었다.

하지만 해밀턴 회로 문제에 대한 다항 시간 엄밀해가 구해지지 않으면(해밀턴 회로 문제는 NP-완전이므로 P≠NP와 동일), 삼각 부등식을 만족하지 않는 TSP는 근사율을 보장하는 다항 시간 알고리즘이 존재하지 않는다.

6. 3. 1. 메트릭 TSP

도시 간 거리가 삼각 부등식을 만족하는 경우를 메트릭 TSP라고 하며, 델타-TSP(Δ-TSP)라고도 부른다.^[35] 이는 도시 간의 거리가 메트릭을 형성하여, ''A''에서 ''B''로 가는 직접적인 연결이 중간 지점 ''C''를 경유하는 것보다 멀지 않다는 조건을 만족하는 것이다.

:

d_{AB} \le d_{AC} + d_{CB}

이러한 조건에서, 간선들은 정점 집합에 대한 메트릭을 구성한다.

메트릭 TSP의 예는 다음과 같다.

유클리드 TSP: 두 도시 사이의 거리는 해당 점들 사이의 유클리드 거리이다.
직교 TSP: 두 도시 사이의 거리는 두 도시의 ''x'' 좌표와 ''y'' 좌표의 차이의 절댓값의 합이다. 이 메트릭은 맨해튼 거리 또는 도시 블록 메트릭이라고도 한다.
최대 메트릭: 두 점 사이의 거리는 ''x'' 좌표와 ''y'' 좌표의 차이의 절댓값의 최댓값이다.

마지막 두 메트릭은 인쇄 회로 기판에 구멍을 뚫는 기계를 라우팅하는 데 사용될 수 있다.

삼각 부등식이 성립하는 TSP에 대해서는 다양한 다항 시간 근사 알고리즘이 존재한다. 예를 들어, 근사 알고리즘이 2인 알고리즘(최근 추가법 등)이나 근사도 1.5인 알고리즘(크리스토피데스 알고리즘)이 알려져 있다.^[35]

6. 3. 2. 비대칭 TSP

유향 그래프를 형성하는 비대칭 TSP는 도시 간 거리가 양방향으로 다른 경우이다. 이는 교통 체증, 일방 통행 도로, 출발 및 도착 요금이 다른 도시 간의 항공 요금 등에서 발생할 수 있다.^[36]

비대칭 TSP의 예시는 다음과 같다.

비대칭 경로 가중치
	A	B	C
A		1	2
B	6		3
C	5	4

비대칭 TSP는 크기 ''N''의 비대칭 행렬을 크기 2''N''의 대칭 행렬로 변환하여 해결할 수 있다.^[36] 변환 과정은 다음과 같다.

1. 그래프의 각 노드를 복제하여 두 번째 ''유령 노드''를 생성한다.

2. 원래 노드와 유령 노드를 매우 낮은 가중치(여기서는 −''w'')의 "유령" 가장자리로 연결한다.

3. 원래 3×3 행렬은 왼쪽 하단, 전치 행렬은 오른쪽 상단에 배치한다.

4. 두 행렬 사본의 대각선은 −''w''로 표현되는 저비용 홉 경로로 대체한다.

대칭 TSP로 변환된 행렬은 다음과 같다.

대칭 경로 가중치
	A	B	C	A′	B′	C′
A				−w	6	5
B				1	−w	4
C				2	3	−w
A′	−w	1	2
B′	6	−w	3
C′	5	4	−w

새 그래프에서 모든 유령 가장자리가 최적 대칭 TSP 솔루션에 속하도록 ''w'' 값을 충분히 낮게 설정해야 한다. 이렇게 하면 각 원래 노드는 유령 노드 옆에 나타나게 되고, 이들을 다시 병합하면 원래 비대칭 문제의 최적 솔루션을 얻을 수 있다.

7. 관련 문제

그래프 이론 관점에서, 주어진 완전 가중 그래프에서 (정점은 도시, 간선은 도로, 가중치는 도로의 비용 또는 거리를 나타냄) 최소 가중치를 갖는 해밀턴 회로를 찾는 것이 외판원 문제와 동일하다. 이는 비완전 무가중 그래프에서 해밀턴 경로(또는 회로)가 존재하는지 묻는 해밀턴 경로 문제보다 더 일반적이다.^[14] 시작 도시로 돌아가야 한다는 제약 조건은 문제의 계산 복잡도를 변경하지 않는다.

병목 여행 외판원 문제는 가장 가중치가 큰 간선의 최소 가중치를 갖는 가중 그래프에서 해밀턴 회로를 찾는 문제이다. 예를 들어 큰 버스로 좁은 거리를 피하는 경우가 있다.^[14] 이 문제는 운송 및 물류 분야 외에도 인쇄 회로 기판 제조에서 드릴 머신의 경로 예약, 로봇 가공 또는 드릴링 응용 분야에서 로봇 재도구 시간(단일 기계 작업 시퀀싱 문제)을 최소화하는 데 활용된다.^[15]

일반화된 여행 외판원 문제는 "여행 정치인 문제"라고도 하며, 각 "주"에서 정확히 하나의 도시를 방문해야 하는 문제이다. 절단 재고 문제에서 칼 변경 횟수를 최소화하거나 반도체 제조에서의 드릴링 등에 응용된다.

순차적 순서 문제는 도시 간에 우선 순위 관계가 존재하는 도시 집합을 방문하는 문제를 다룬다.

여행 구매자 문제는 여러 도시에서 다양한 가격으로 제품을 구매할 때 총 비용(여행 비용 + 구매 비용)을 최소화하고 필요한 모든 제품을 구매할 수 있는 경로를 찾는 문제이다.

분석가의 외판원 문제는 기하 측정 이론에서 어떤 조건 하에서 유클리드 공간의 부분 집합이 가측 곡선에 포함될 수 있는지 묻는 문제이다.

8. 벤치마크

TSPLIB는 외판원 문제(TSP) 및 관련 문제들의 샘플 인스턴스 라이브러리이다.^[61] 벤치마크 목적으로 유지되며, 실제 도시 목록과 인쇄 회로 기판 레이아웃 등 다양한 문제들을 포함하고 있다.

참조

_[1] 논문 The Ring Star Problem: Polyhedral analysis and exact algorithm 2004-05
_[2] 웹사이트 See the TSP world tour problem which has already been solved to within 0.05% of the optimal solution. http://www.math.uwat[...]
_[3] 웹사이트 Der Handlungsreisende – wie er sein soll und was er zu tun hat, um Aufträge zu erhalten und eines glücklichen Erfolgs in seinen Geschäften gewiß zu sein – von einem alten Commis-Voyageur https://zs.thulb.uni[...]
_[4] 서적 A discussion of the early work of Hamilton and Kirkman can be found in Graph Theory, 1736–1936 Clarendon Press 1986
_[5] 문서 Cited and English translation in Schrijver (2005). Original German: "Wir bezeichnen als Botenproblem (weil diese Frage in der Praxis von jedem Postboten, übrigens auch von vielen Reisenden zu lösen ist) die Aufgabe, für endlich viele Punkte, deren paarweise Abstände bekannt sind, den kürzesten die Punkte verbindenden Weg zu finden. Dieses Problem ist natürlich stets durch endlich viele Versuche lösbar. Regeln, welche die Anzahl der Versuche unter die Anzahl der Permutationen der gegebenen Punkte herunterdrücken würden, sind nicht bekannt. Die Regel, man solle vom Ausgangspunkt erst zum nächstgelegenen Punkt, dann zu dem diesem nächstgelegenen Punkt gehen usw., liefert im allgemeinen nicht den kürzesten Weg."
_[6] 서적 The Travelling Salesman Problem: A Guided Tour of Combinatorial Optimization https://google.com/b[...] John Wiley & sons 1985
_[7] 간행물 On the Hamiltonian game (a traveling salesman problem) https://apps.dtic.mi[...] The RAND Corporation 2020-05-02
_[8] 문서 A detailed treatment of the connection between Menger and Whitney as well as the growth in the study of TSP can be found in Schrijver (2005).
_[9] 논문 A historical note on the 3/2-approximation algorithm for the metric traveling salesman problem
_[10] 간행물 Computer Scientists Find New Shortcuts for Infamous Traveling Salesman Problem https://www.wired.co[...] 2015-06-14
_[11] 웹사이트 Computer Scientists Break Traveling Salesperson Record https://www.quantama[...] 2020-10-13
_[12] 간행물 STOC '21: 53rd Annual ACM SIGACT Symposium on Theory of Computing, Virtual Event, Italy, June 21-25, 2021
_[13] 간행물 Traveling salesman problem heuristics: leading methods, implementations and latest advances
_[14] 웹사이트 How Do You Fix School Bus Routes? Call MIT in Wall street Journal http://online.WSJ.co[...]
_[15] 간행물 New Efficient Transformation of the Generalized Traveling Salesman Problem into Traveling Salesman Problem
_[16] 서적 Combinatorial optimization: algorithms and complexity Dover
_[17] 문서 On Directed Graphs and Integer Programs IBM Mathematical research Project (Princeton University) 1960
_[18] 서적 Linear Programming and Extensions PrincetonUP 1963
_[19] 논문 Short combinatorial proof that the DFJ polytope is contained in the MTZ polytope for the Asymmetric Traveling Salesman Problem
_[20] 논문 Requiem for the Miller–Tucker–Zemlin subtour elimination constraints?
_[21] 문서 Integer Programming Formulation of Traveling Salesman Problems. 1960
_[22] 논문 Solution of a Large-Scale Traveling-Salesman Problem 1954-11
_[23] 문서 Bellman (1960), Bellman (1962), Held Karp (1962)
_[24] 서적 Proceedings of the Thirtieth Annual ACM-SIAM Symposium on Discrete Algorithms
_[25] Youtube Traveling Salesman Problem - Branch and Bound
_[26] 웹사이트 Optimal Tour of Sweden http://www.math.uwat[...] 2020-11-11
_[27] 논문 Traveling salesman should not be greedy: domination analysis of greedy-type heuristics for the TSP 2002-03-15
_[28] 간행물 Experimental Analysis of Heuristics for the ATSP Springer, Boston, MA 2007
_[29] 간행물 Approximate algorithms for the traveling salesperson problem 1974-10-14
_[30] 논문 Genetic Operators for Combinatorial Optimization in TSP and Microarray Gene Ordering
_[31] 논문 Match Twice and Stitch: A New TSP Tour Construction Heuristic
_[32] 서적 Local Search in Combinatorial Optimisation John Wiley and Sons Ltd. 1997
_[33] 논문 Constricting Insertion Heuristic for Traveling Salesman Problem with Neighborhoods https://cse.cs.ovgu.[...] 2013-06-02
_[34] 논문 Ant Colonies for the Traveling Salesman Problem
_[35] 논문 On some properties of shortest Hamiltonian circuits
_[36] 논문 Transforming asymmetric into symmetric traveling salesman problems
_[37] 논문 Beardwood–Halton–Hammersley theorem for stationary ergodic sequences: a counterexample
_[38] 논문 The shortest path and the shortest road through n points 1955
_[39] 논문 A parallel tabu search algorithm for large traveling salesman problems 1994
_[40] 논문 The Traveling Salesman Problem and Minimum Spanning Trees 1970
_[41] 논문 Probabilistic analysis of the Held and Karp lower bound for the Euclidean traveling salesman problem 1991
_[42] 웹사이트 error https://about.att.co[...]
_[43] 웹사이트 Christine L. Valenzuela and Antonia J. Jones http://users.cs.cf.a[...] 2007-10-25
_[44] 보고서 On approximation preserving reductions: Complete problems and robust measures' Department of Computer Science, University of Helsinki
_[45] 논문 О некоторых экстремальных обходах в графах http://nas1.math.nsc[...] 1978
_[46] 서적 Proceedings of the 50th Annual ACM SIGACT Symposium on Theory of Computing ACM Press 2018
_[47] 서적 Proceedings of the 52nd Annual ACM SIGACT Symposium on Theory of Computing ACM 2020-06-08
_[48] 논문 Human performance on the traveling salesman problem 1996-06
_[49] 논문 Human Performance on Visually Presented Traveling Salesperson Problems with Varying Numbers of Nodes 2006
_[50] 논문 Convex hull and tour crossings in the Euclidean traveling salesperson problem: Implications for human performance studies 2003-03-01
_[51] 논문 Human Performance on the Traveling Salesman and Related Problems: A Review 2011
_[52] 논문 Convex hull or crossing avoidance? Solution heuristics in the traveling salesperson problem 2004-03-01
_[53] 논문 Intelligence and individual differences in performance on three types of visually presented optimisation problems
_[54] 논문 Acknowledging crossing-avoidance heuristic violations when solving the Euclidean travelling salesperson problem 2017-06-12
_[55] 논문 Sense of direction and conscientiousness as predictors of performance in the Euclidean travelling salesman problem 2017-01-11
_[56] 논문 Human behaviour in the Euclidean Travelling Salesperson Problem: Computational modelling of heuristics and figural effects 2018-12
_[57] 논문 Human performance on the traveling salesman and related problems: A review https://docs.lib.pur[...]
_[58] 간행물 "Journal of Problem Solving'' 1(1)" https://docs.lib.pur[...] 2014-06-06
_[59] 논문 Let the pigeon drive the bus: pigeons can plan future routes in a room 2012-05-01
_[60] 논문 Computation of the travelling salesman problem by a shrinking blob http://www.phychip.e[...] 2014
_[61] 웹사이트 TSPLIB http://comopt.ifi.un[...] 2020-10-10
_[62] 간행물 'Travelling Salesman' movie considers the repercussions if P equals NP https://www.wired.co[...] 2012-04-26
_[63] 뉴스 When the Mona Lisa is NP-Hard https://blogs.scient[...] Scientific American 2015-04-31

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com