적합도

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 적응도의 정의 및 측정
3. 적응도 모델
- 3.1. 선택에 의한 유전자형 빈도 변화
4. 적응도 지형
5. 포괄 적응도
6. 유전적 부하
7. 적응도의 역사
8. 계산 과학에서의 응용
참조

1. 개요

적응도는 생물 개체가 환경에 얼마나 적응했는지를 나타내는 개념으로, 개체의 번식 성공 능력을 총체적으로 파악하는 지표이다. 절대 적응도와 상대 적응도로 구분되며, 세대 간 유전자형 빈도 변화를 통해 정량화된다. 절대 적응도는 다음 세대 개체 수를 이전 세대 개체 수로 나눈 값이며, 상대 적응도는 특정 유전형질이 다음 세대에 나타나는 비율을 의미한다. 적응도 지형은 유전자형과 적응도의 관계를 시각화한 모델이며, 포괄 적응도는 자손뿐 아니라 친족에게까지 적응도를 확대한 개념이다. 유전자 부하는 집단의 평균 적응도를 측정하는 지표이며, 계산 과학에서는 유전자 알고리즘의 적합도 함수로 활용된다.

더 읽어볼만한 페이지

집단유전학 - 근친교배
근친교배는 유전적으로 가까운 개체 간의 교배를 의미하며, 유전 질환 발현 가능성을 높이는 등 생물학적 영향과 품종 개량 및 연구에 활용된다.
집단유전학 - 유전적 부동
유전적 부동은 집단 내 대립형질 빈도가 무작위로 변하는 현상으로, 집단 크기가 작을수록 영향이 커지며 자연 선택과 함께 작용하여 진화에 영향을 미친다.

적합도
적응도
정의	특정 환경에서 개체가 생존하고 번식하는 능력
측정	자손 수 또는 유전자 풀에 기여하는 비율
관련 개념	자연 선택 진화 유전적 부동
개요
설명	적응도는 개체가 특정 환경에 얼마나 잘 "맞는지"를 나타내는 지표이며, 생존과 번식 성공을 통해 측정된다.
구성 요소	생존 능력 짝짓기 능력 자손 수
적응도 경관
개념	다양한 유전자형의 적응도를 시각적으로 표현한 지도
활용	진화 과정을 이해하고 예측하는 데 사용됨
설명	적응도 경관에서 높은 지점은 높은 적응도를 나타내며, 낮은 지점은 낮은 적응도를 나타낸다.
수학적 정의
절대적응도 (W)	개체가 다음 세대에 전달하는 자손의 평균 수
상대적응도 (w)	다른 유전자형에 비해 특정 유전자형의 적응도 (보통 가장 흔한 유전자형의 적응도를 1로 설정)
계산	절대적응도: W = (특정 유전자형의 자손 수) / (전체 개체 수) 상대적응도: w = W / (가장 높은 W)
유전자 중심 관점
개념	개체가 아닌 유전자를 진화의 기본 단위로 보는 관점
설명	유전자는 자신의 복제를 극대화하기 위해 개체의 행동을 조종한다고 본다.
예시	이타적 행동은 자신의 유전자와 동일한 유전자를 가진 다른 개체의 생존과 번식을 돕는 행동으로 설명될 수 있다.
적응도의 변화
요인	환경 변화 돌연변이 유전자 흐름 유전적 부동
결과	진화적 적응 종 분화 멸종
중요성
진화 연구	자연 선택의 작용을 이해하고 예측하는 데 필수적이다.
의학	항생제 내성, 암 진화 등 질병의 진화를 이해하는 데 도움이 된다.
농업	작물 품종 개량, 해충 방제 등에 응용될 수 있다.

2. 적응도의 정의 및 측정

적응도는 특정 생물 개체가 주어진 환경에 얼마나 잘 적응하고 있는지를 나타내는 척도이다. 이는 생존과 번식에 영향을 미치는 다양한 형질들을 포괄적으로 고려하며, 한 생물이 성공적으로 다음 세대에 유전자를 전달하는 능력을 종합적으로 평가하는 개념이다. 찰스 다윈 시대에도 유사한 의미로 사용되었으며, 오늘날에도 "적응도가 높다"는 표현은 생존과 번식에 유리한 특성을 가졌다는 의미로 쓰인다.

현대 진화생물학에서는 적응도를 보다 구체적으로 정의하며, 크게 절대 적응도와 상대 적응도로 나누어 측정한다. 자연 선택설에 따르면 더 많은 자손을 성공적으로 남기는 개체가 선택되므로, 적응도는 세대 간 유전자형 빈도 변화를 통해 정량화될 수 있다.

절대 적응도: 특정 개체나 유전자형이 다음 세대에 남기는 자손의 절대적인 수를 의미한다. 예를 들어, 번식 가능한 연령까지 살아남은 자식의 수로 정의될 수 있다.
상대 적응도: 집단 내 다른 개체나 유전자형과 비교했을 때 특정 유전자형이 다음 세대에 유전자를 전달하는 상대적인 성공률을 나타낸다. 이는 특정 대립 유전자가 집단 내에서 시간이 지남에 따라 빈도가 어떻게 변하는지를 보여주는 척도로, 집단 유전학 등에서 중요하게 사용된다.

2. 1. 절대 적응도

'''절대 적응도'''(

w_{\mathrm{abs}}

)는 특정 유전자를 갖고 있는 이전 세대의 수에 대한 다음 세대의 수의 비이다. 값이 1.0 이상이면 유전형질 발현빈도의 증가를 뜻하고 1.0 미만이면 감소를 뜻한다.

{w_{\mathrm{abs}}} = } \over {N_{\mathrm{before}}}}

유전자형의 절대 적합도(

W

)는 선택에 기인하여 한 세대 동안 해당 유전자형의 풍부함이 비례적으로 변화하는 것으로 정의된다. 예를 들어,

n(t)

가 무한히 큰 개체군에서 세대

t

의 유전자형 풍부함이고 (유전 부동으로 인한 변화를 무시) 돌연변이로 인한 유전자형 풍부함의 변화를 무시하면,^[4]

n(t+1)=Wn(t)

절대 적합도가 1보다 크면 해당 유전자형의 풍부함이 증가한다는 것을 나타내고, 1보다 작으면 감소한다는 것을 나타낸다.

단어 그대로 이해하면, 해당 생물 개체가 얼마나 그 생활 환경에 적응하고 있는지를 나타내는 값이다. 그러나 여기에는 출산 수나 출산 간격 등 직접적으로 번식과 관련된 특성뿐만 아니라 근력, 시력, 신체 크기와 같은 많은 특성도 간접적으로 관련된다. 이로 인해 적응도는 해당 개체가 생물로서 번영해 나가는 능력을 총체적으로 파악하기 위한 개념으로 이해할 수 있다. 찰스 다윈 시대에 사용된 적응도(Fitness)는 이러한 의미이며, 현재에도 "적응적(살아남기에 적합한 성질일 것이다)"과 동일한 의미로 "적응도가 높다"라고 사용하기도 한다.

현재 일반적으로 사용되는 정의는, 자연 선택설의 생각에 입각하여, 더 많은 자식을 남기는 것이 선택되므로, "'''어떤 생물 개체가 그 생애에 낳은 다음 세대 자식 중, 번식 연령까지 성장할 수 있었던 자식의 수'''"가 된다. 동물학 등의 현장 연구나 실험에서는 유전적 적응도를 측정하는 것은 어렵기 때문에, 이 정의를 근사값으로 사용한다. 이것을 개체 적응도라고 부른다. 또한 자식의 절대적인 수로 나타내는 적응도를 절대 적응도라고 부른다. 개체수가 안정된 환경에서는, 평균적인 절대 적응도는 1이다. 그러나 번식 전략에 따라서는, 다음 세대의 자식 수가 같더라도 손자의 수에 차이가 생길 수도 있다 (「피셔의 원리」도 참조). 따라서 더 정확한 (엄밀하지는 않지만) 표현으로는 "충분히 먼 미래의 어떤 세대에 남은 자손의 수"라고 할 수 있다.

2. 2. 상대 적응도

'''상대 적응도'''는 다음 세대에 출현한 유전형질들 가운데 관찰하고자 하는 특정한 유전형질이 나타난 비율을 뜻한다. 따라서 상대 적응도의 값은 0에서 1 사이에 놓이게 된다.

실제 관찰에서는 절대 적응도를 측정하기 어렵기 때문에 (엄격한 실험 통제가 있지 않는 한) 대부분의 관찰은 상대 적응도를 통해 이루어진다. 그러나 유전형질 발현 빈도의 변화라는 관점에서 보면 절대 적응도와 상대 적응도는 다음의 식과 같은 연관을 갖고 있기 때문에 상대 적응도의 변화 역시 유의미한 결과로 받아들일 수 있다.

:

{\frac{w_{abs}}{\overline{w}_{abs}} = \frac{w_{rel}}{\overline{w}_{rel}}}

생물학자들은 세대 간의 변화가 누적될 때의 적응도 변화를 주로 다루기 때문에 적응도를 하나의 계수로 취급하며, 그의 로그를 취해 적응도의 변화를 추적하기도 한다. 미국의 생물학자 서얼 라이트는 전반적인 적응도의 변화 과정을 평가하기 위해 적응 경향이라는 개념을 도입하였다.

절대 적응도가 유전자형의 절대적인 수 변화를 결정하는 반면, 상대 적응도(

w

)는 유전자형의 빈도 변화를 결정한다. 만약

N(t)

가 세대

t

의 총 개체수이고 특정 유전자형의 빈도가

p(t)=n(t)/N(t)

라면, 다음 세대(

t+1

)에서의 빈도는 다음과 같이 표현될 수 있다.

:

p(t+1)=\frac{w}{\overline{w}}p(t)

여기서

\overline{w}

는 개체군 내 평균 상대 적응도를 의미한다 (유전적 부동이나 돌연변이로 인한 빈도 변화는 제외). 상대 적응도는 서로 다른 유전자형의 상대적인 유행 변화만을 나타내므로, 각 유전자형의 상대적인 값만 중요하다. 상대 적응도는 0을 포함한 모든 음수가 아닌 값을 가질 수 있으며, 종종 특정 유전자형을 기준으로 삼아 그 상대 적응도를 1로 설정하는 것이 계산에 편리하다. 상대 적응도는 Wright–Fisher 모델이나 모란 모델과 같은 집단 유전학 모델에서 사용된다.

절대 적응도를 이용하여 상대 적응도를 계산할 수도 있다.

p(t+1)=n(t+1)/N(t+1)=(W/\overline{W})p(t)

이고, 여기서

N(t+1)=\overline{W} N(t)

이며

\overline{W}

는 개체군의 평균 절대 적응도이다. 이를 통해

w/\overline{w}=W/\overline{W}

라는 관계를 알 수 있으며, 즉 상대 적응도는 절대 적응도의 평균값(

\overline{W}

)에 대한 각 유전자형의 절대 적응도(

W

)의 비율(

W/\overline{W}

)에 비례한다. 그러나 상대 적응도만으로는 절대 적응도를 계산할 수 없는데, 이는 상대 적응도가 전체 개체수(

N(t)

)의 변화에 대한 정보를 포함하지 않기 때문이다.

유전자형에 상대 적응도 값을 할당하는 것이 수학적으로 적절하려면 두 가지 조건이 충족되어야 한다. 첫째, 개체군은 인구 통계학적으로 평형 상태에 있어야 한다. 둘째, 개체들은 출생률, 경쟁 능력, 또는 사망률 중 어느 한 특성에서 차이를 보여야 하며, 이러한 특성들의 조합에서 차이를 보여서는 안 된다.^[5]

일반적으로 '적응도'라는 단어는 해당 생물 개체가 생활 환경에 얼마나 잘 적응하고 있는지를 나타내는 값으로 이해될 수 있다. 여기에는 출산 수나 간격 같은 직접적인 번식 특성뿐만 아니라, 근력, 시력, 신체 크기 등 간접적으로 생존과 번식에 영향을 미치는 많은 특성들이 포함된다. 찰스 다윈 시대에 사용된 적응도(Fitness)는 이러한 포괄적인 의미를 가졌으며, 현재에도 "적응도가 높다"는 표현은 "살아남기에 적합한 성질을 가졌다"는 의미로 사용되기도 한다.

하지만 현재 집단 유전학이나 수리 생태학 등에서 일반적으로 사용되는 '적응도'는 좀 더 구체적인 정의를 가진다. 자연 선택설에 따르면 더 많은 자손을 남기는 개체가 선택되므로, 적응도는 흔히 "어떤 생물 개체가 평생 낳은 자식 중 번식 연령까지 성장할 수 있었던 자식의 수"로 정의된다. 이를 '개체 적응도' 또는 '절대 적응도'라고 부른다. 동물학 등의 현장 연구나 실험에서는 유전적 적응도를 직접 측정하기 어렵기 때문에 이 정의를 근사값으로 사용한다. 개체수가 안정된 환경에서는 평균 절대 적응도는 1에 가깝다. 그러나 번식 전략에 따라 다음 세대의 자식 수가 같더라도 손자 세대의 수에 차이가 생길 수 있으므로( 피셔의 원리 참조), 더 정확하게는 "충분히 먼 미래 세대에 남는 자손의 수"로 이해할 수도 있다.

한편, '유전적 적응도'는 "어떤 형질을 나타내는 대립 유전자 (또는 진화 게임 이론에서의 전략)가 집단 내에서 퍼져나가는 상대적인 속도"를 의미하며, 이것이 바로 '상대 적응도'이다. 예를 들어, 유전자 X를 가진 개체가 평균 6마리의 자손을 남기고, 대립 유전자 Y를 가진 개체가 평균 4마리의 자손을 남긴다고 가정하자. 이 집단의 평균 자손 수는 (6 + 4) / 2 = 5마리이다. 이때 유전자 X의 상대 적응도는 6 / 5 = 1.2가 되고, 유전자 Y의 상대 적응도는 4 / 5 = 0.8이 된다. 집단 전체의 평균 상대 적응도는 항상 1이다. 특정 유전자의 상대 적응도가 1이면 그 유전자의 빈도는 변하지 않고, 1보다 작으면 빈도가 점차 감소하며, 1보다 크면 빈도가 점차 증가한다. 값이 클수록 더 빠르게 퍼져나간다. 위의 예시에서는 상대 적응도가 1.2인 유전자 X의 빈도가 집단 내에서 증가하게 된다.

2. 3. 적응도와 확률

적합성은 단순히 실제 낳은 자손의 수로만 정의되는 것이 아니라, 자손을 남길 수 있는 성향이나 확률로 정의되기도 한다.^[2] 예를 들어, 메이너드 스미스(John Maynard Smith)는 적합성을 개별 생명체가 아닌, 특정 유전자형을 가진 개체들의 집단 전체가 가지는 속성으로 보았다. 여기서 말하는 '기대 자손 수'는 어떤 한 개체가 낳는 자손의 수가 아니라, 그 집단에 속한 개체들이 평균적으로 낳을 것으로 기대되는 자손의 수를 의미한다. 만약 특별한 유전자를 가진 첫 아기가 우연히 벼락에 맞아 죽었다고 해도, 그것이 그 유전자형의 적합성이 낮다는 증거는 아니며 단지 그 아기가 불운했을 뿐이라는 것이다.^[2]

다른 관점에서는 "개인의 적합성이란, 특정 표현형의 배열 x를 가진 개체가 다음 세대의 부모가 될 집단에 포함될 확률 s(x)"로 정의하기도 한다.^[3]

'적응도'라는 말 자체는 해당 생물이 환경에 얼마나 잘 적응하고 있는지를 나타내는 값으로 이해할 수 있다. 여기에는 번식과 직접 관련된 출산 수나 간격뿐 아니라, 근력, 시력, 몸 크기 등 다양한 특성들이 간접적으로 영향을 미친다. 따라서 적응도는 생물이 성공적으로 번성해 나가는 능력을 종합적으로 보여주는 개념으로 볼 수 있다. 찰스 다윈 시대에 사용된 적응도(Fitness)는 이러한 의미를 담고 있으며, 오늘날에도 "적응도가 높다"는 표현은 "살아남기에 적합한 성질을 가졌다"는 의미로 쓰이기도 한다.

3. 적응도 모델

무성생식 개체군에서 유전자 재조합이 없는 제한적인 상황을 가정하면, 성과 재조합의 복잡성을 피하여 적합성 개념을 보다 명확하게 정의할 수 있다. 이러한 조건 하에서는 적합성을 특정 유전자형에 직접 할당하는 것이 가능하다. 적합성을 이해하고 측정하는 데에는 일반적으로 두 가지 방식이 사용되는데, 바로 절대적 적합성(absolute fitness)과 상대적 적합성(relative fitness)이다.

3. 1. 선택에 의한 유전자형 빈도 변화

다른 유전자형보다 상대 적합도가 1% 더 높은 유전자형 $A$ 의 시간에 따른 빈도 증가. $B$ 는 상대적으로 빈도가 감소한다.

선택에 의한 유전자형 빈도의 변화는 상대 적합도의 정의로부터 바로 유도될 수 있다. 특정 유전자형의 다음 세대 빈도 변화(

\Delta p

)는 현재 세대의 빈도(

p(t)

)와 그 유전자형의 적합도(

w

), 그리고 집단의 평균 적합도(

\overline{w}

)를 이용하여 다음과 같이 표현된다.

:

\Delta p = p(t+1)-p(t)=\frac{w-\overline{w}}{\overline{w}}p(t)

이 식은 어떤 유전자형의 빈도가 증가할지 감소할지는 해당 유전자형의 적합도가 집단 전체의 평균 적합도보다 높은지 낮은지에 따라 결정된다는 것을 보여준다. 즉, 평균보다 적합도가 높으면 그 유전자형의 빈도는 증가하고, 낮으면 감소한다.

만약 집단 내에 두 가지 유전자형

A

와

B

만 존재한다고 가정해보자. 각각의 적합도를

w_A

와

w_B

라 하고, 빈도를

p

와

1-p

라고 하면, 평균 적합도는

\overline{w}=w_A p + w_B (1-p)

가 된다. 이때 유전자형

A

의 빈도 변화는 다음과 같이 나타낼 수 있다.

:

\Delta p = \frac{w_A-\overline{w}}{\overline{w}}p = \frac{w_A-(w_A p + w_B (1-p))}{w_A p + w_B (1-p)}p = \frac{w_A(1-p) - w_B(1-p)}{w_A p + w_B (1-p)}p = \frac{w_A-w_B}{\overline{w}}p(1-p)

이 식에서 볼 수 있듯이, 유전자형

A

의 빈도 변화는 두 유전자형의 적합도 차이(

w_A-w_B

)에 직접적으로 영향을 받는다.

만약

A

가

B

보다 더 적합하다고 가정하고, 두 적합도의 차이를 나타내는 선택 계수

s

를

w_A=(1+s)w_B

(

s > 0

)로 정의하면, 빈도 변화 식은 다음과 같이 근사할 수 있다.

:

\Delta p = \frac{s w_B}{\overline{w}}p(1-p) = \frac{s w_B}{(1+s)w_B p + w_B (1-p)}p(1-p) = \frac{s}{1+sp}p(1-p)

만약 선택 계수

s

가 매우 작다면 (

s \ll 1

), 분모의

1+sp

는 거의 1에 가까워지므로, 식은 다음과 같이 더욱 단순화될 수 있다.

:

\Delta p \approx sp(1-p)

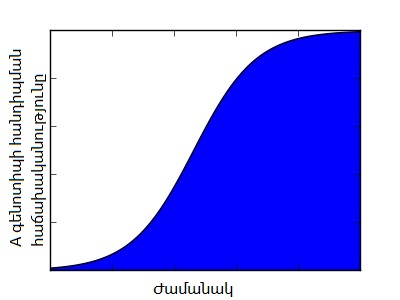
이 식은 로지스틱 함수의 미분 형태와 유사하며, 이는 더 적합한 유전자형의 빈도가 시간이 지남에 따라 S자 곡선 형태, 즉 로지스틱하게 증가하는 경향을 보인다는 것을 의미한다. 위 그림은 이러한 빈도 변화의 예시를 보여준다.

4. 적응도 지형

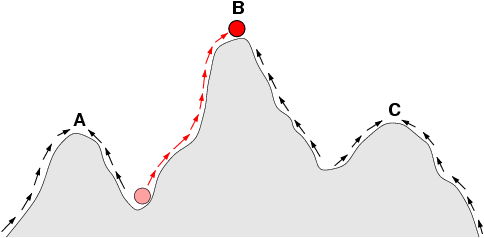
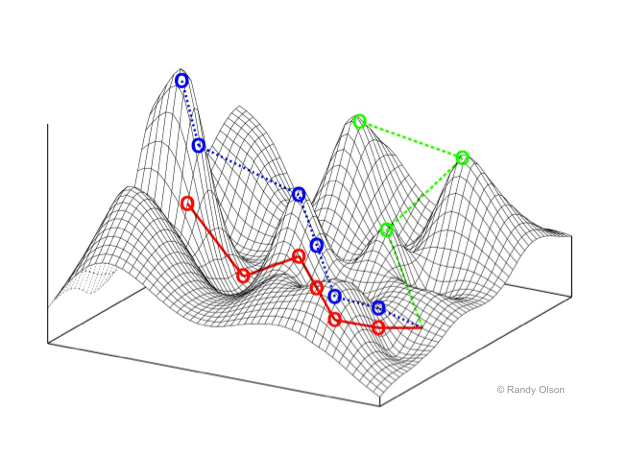
적합도 지형의 개략도. 화살표는 적합도 지형상의 개체군의 이동을 나타내며, A점과 C점이 국소적인 최적값을 나타낸다. 빨간색 원은 매우 낮은 적합도의 개체군이 가장 좋은 적합도를 획득할 때의 이동 방식을 나타낸다.

3차원 공간으로 나타낸 NK 모델을 기반으로 한 적합도 지형. 진화의 경로는 복수 존재한다.

적합도 지형(fitness landscape^영어)은 1923년에 시월 라이트 등이 제창한, 유전자형과 생식 성공률(적합도)의 관계를 시각화하기 위해 사용되는 수학적 모델이다. 예를 들어 2차원 공간에 개체군의 각 생물 개체를 배치했다고 가정하면, 거기에 "높이" 축을 추가하고 그 축의 값에 적응률을 적용하여 기복이 있는 곡면을 얻을 수 있다. 이 곡면을 적합도 지형이라고 부른다.

적합도 지형의 개념을 사용하면, 적합도가 높은 개체가 그 수를 늘리고 낮은 개체는 수를 줄여가는 모습을 설명하기 쉽다. 적합도가 높은 개체는 적합도 지형 안에서 "높이"가 높은 위치에 있으며, 적합도가 낮은 개체는 낮은 위치에 있다. 개체군은 더 많은 개체를 높은 위치에 두려고 하며, 낮은 위치의 개체는 점차 수를 줄이고 높은 위치에 있는 개체의 수를 늘리는 방식으로 번식을 한다. 그림으로 나타냈을 때 이것은 마치 곡면의 기복을 오르는 것처럼 보인다.

5. 포괄 적응도

적응도를 어떤 개체의 자손뿐만 아니라 그 친족, 또는 같은 대립 유전자를 가질 가능성이 있는 다른 개체에게까지 확대한 것을 포괄 적응도라고 한다. 사회성 행동의 진화를 다룰 때에는 포괄 적응도를 사용해야 한다. 이 경우에는 보통 자식에게도 포괄 적응도에서의 혈연도 계산이 적용된다. (유성 생식에서는 자식의 유전적 가치는 부모의 절반이며, 이는 부모 자식 간의 진화적 갈등의 원인이 되기도 한다.) 포괄 적응도는 유전적 적응도의 개념 중 하나이며, 포괄 적응도를 단순히 개체 수로 계산하면 혼란을 일으킬 수 있다.

포괄 적응도의 상승은 어떤 사회적 행동이 유전자의 다음 세대 전달에 미치는 효과를 설명하는 데 사용된다. 예를 들어, 자신이 친족을 도움으로써 그 친족이 더 많은 자손을 남기게 되었다면, 자신의 "이타적 행동에 관련된 대립 유전자"의 포괄 적응도는 상승한 것으로 본다. 반대로, 전혀 다른 지역으로 이주하여 서로 영향을 줄 수 없게 된 친족이 자손을 낳는 것은 자신의 포괄 적응도 상승과는 관련이 없다.

적응도라는 개념 자체를 처음 제안하고 수학적 모델로 만든 것은 집단 유전학자인 로널드 피셔, J. B. S. 홀데인, 슈월 라이트 등이었다. 이후 W. D. 해밀턴은 이 개념을 확장하여 포괄 적응도를 제창했다. 더 나아가 G. 프라이스는 공분산 법칙을 도입하여 포괄 적응도를 친족뿐만 아니라 더 넓은 범위의 개체들에게도 적용할 수 있도록 개념을 확장했다.

6. 유전적 부하

유전자 부하는 집단의 평균 적합도를 측정하는 지표로, 가장 높은 적합도를 가진 이론적인 유전자형 또는 실제 집단에 존재하는 가장 적합한 유전자형과 비교하여 상대적으로 측정된다.^[7] 예를 들어, n개의 유전자형 $\mathbf{A} _1 \dots \mathbf{A} _n$ 이 있고, 각각의 적합도가 $w_1 \dots w_n$ , 유전자형 빈도가 $p_1 \dots p_n$ 라고 가정해 보자. 빈도 의존 선택을 무시하면, 유전자 부하( $L$ )는 다음과 같이 계산할 수 있다.

: $L = {{w_\max - \bar w}\over w_\max}$

여기서 $w_\max$ 는 최대 적합도이고, $\bar w$ 는 집단의 평균 적합도를 의미한다. 즉, 유전자 부하는 집단의 평균 적합도가 이론적인 최적 상태에 비해 얼마나 낮은지를 나타낸다.

유전자 부하는 여러 요인에 의해 증가할 수 있다. 유해한 돌연변이가 발생하거나, 외부 집단으로부터 적응도가 낮은 개체가 이주해오거나, 근친 교배 또는 원교 배가 일어나 집단의 평균 적합도가 낮아지면 유전자 부하가 커진다. 또한, 유익한 돌연변이가 나타나 최대 적합도( $w_\max$ ) 자체가 높아지는 경우에도 유전자 부하가 증가할 수 있다. 이는 새로운 최적 상태에 비해 기존 집단의 평균 적합도가 상대적으로 낮아지기 때문이며, 이러한 현상을 홀데인의 딜레마(대체 부하 또는 선택 비용)라고 부른다.

7. 적응도의 역사

영국의 사회학자 허버트 스펜서는 1864년 자신의 저서 《생물학의 원리》에서 찰스 다윈이 자연 선택이라고 명명한 개념을 설명하기 위해 "적자생존"이라는 표현을 처음 사용했다.^[6]

영국계 인도 생물학자 J.B.S. 홀데인은 1924년에 발표한 논문 《자연 선택과 인공 선택에 대한 수학적 이론》을 통해, 다윈주의와 멘델 유전학을 통합한 현대 진화론적 종합의 관점에서 처음으로 적합도를 수치적으로 정량화하려는 시도를 했다. 이후 1964년, 영국의 생물학자 W.D. 해밀턴은 《사회적 행동의 유전적 진화》라는 논문에서 포괄 적합도라는 개념을 제시하며 적합도 이론을 더욱 발전시켰다.

8. 계산 과학에서의 응용

자연 선택설을 계산 문제 해결에 응용한 유전자 알고리즘, 진화적 계산 등에서는 개체^[8]가 가진 다양한 특징으로부터 적합도를 계산하여 각 개체가 주어진 문제에 얼마나 적합한지를 평가한다. 이때 적합도를 계산하는 함수를 적합도 함수(Fitness function^영어)라고 부른다.

적합도 함수는 최적화 문제에서 목적 함수와 유사한 역할을 수행한다. 계산된 적합도가 높은 개체는 다음 세대에 자신의 유전적 정보를 전달할 확률이 높아지고(많은 자손^[9]을 남기고), 적합도가 낮은 개체는 점차 도태되어(자손을 거의 남기지 못하고 최종적으로 절멸) 문제의 해에 점진적으로 가까워지게 된다.

적합도 함수는 유전자 알고리즘의 성능에 큰 영향을 미친다. 이상적인 적합도 함수는 해결하려는 문제의 목표와 밀접하게 연관되어 있어야 하며, 계산 속도가 빨라야 한다. 유전자 알고리즘은 여러 세대에 걸쳐 반복적으로 적합도를 계산해야 하므로, 적합도 함수의 실행 속도는 전체 알고리즘의 효율성에 매우 중요하다.

하지만 실제 문제에서는 적합도 함수를 명확하게 정의하기 어려운 경우가 많다. 때로는 적합도 함수를 어떻게 설계해야 할지조차 불분명할 수 있으며, 유전자 알고리즘을 통해 얻어진 최적해가 기대했던 결과와 다를 경우 적합도 함수를 수정하며 반복적으로 알고리즘을 실행해야 한다. 이러한 이유로, 경우에 따라서는 유전자 알고리즘이 생성한 해의 평가를 외부 에이전트(주로 사람)에게 맡기는 방식(대화형 유전자 알고리즘 등)을 사용하기도 한다.

한편, 적합도 지형(fitness landscape^영어) 개념은 최적화 문제에서도 유용하게 사용된다. 언덕 오르기 알고리즘, 최급강하법, 공액 기울기법, 담금질 기법과 같은 다양한 최적화 알고리즘들은 문제의 해 공간을 나타내는 적합도 지형 위에서 가장 좋은 값(최댓값 또는 최솟값)을 찾아가는 과정으로 이해할 수 있다.

참조

_[1] 간행물 Fitness fallacies Natural History 1986
_[2] 서적 Evolutionary Genetics 1989
_[3] 서적 A Primer of Population Genetics 1981
_[4] 서적 An introduction to population genetics theory Blackburn Press 1970
_[5] 논문 Density-dependent selection and the limits of relative fitness 2019-01
_[6] 웹사이트 Letter 5140 – Wallace, A. R. to Darwin, C. R., 2 July 1866 http://www.darwinpro[...] Darwin Correspondence Project 2010-01-12
_[6] 웹사이트 Letter 5145 – Darwin, C. R. to Wallace, A. R., 5 July (1866) http://www.darwinpro[...] Darwin Correspondence Project 2010-01-12
_[6] 인용 Better Competition Advocacy http://works.bepress[...] 2007-08-29
_[7] 서적 Mathematical population genetics. https://archive.org/[...] Springer 2003
_[8] 문서 問題の解の候補となるもの。
_[9] 문서 個体の一部を書き換えたもの。
_[10] 문서 遺伝子型と呼ぶ。

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com