로지스틱 함수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

로지스틱 함수는 1838년 피에르 프랑수아 베르훌스트가 인구 성장 모델로 처음 소개한 함수이다. 이 함수는 초기에는 지수적으로 증가하다가 포화 단계에 접어들면서 선형적으로 둔화되는 특징을 가지며, 수학적 성질, 쌍곡 탄젠트 함수와의 관계, 미분, 적분 등 다양한 특징을 갖는다. 생태학의 개체군 성장 모델, 통계학 및 머신 러닝, 의학의 종양 성장 및 전염병 모델링, 화학, 물리학, 광학, 언어학, 농업, 경제학 및 사회학 등 다양한 분야에서 응용된다.

더 읽어볼만한 페이지

개체군 - 지리학
지리학은 지구와 천체의 특징, 현상, 그리고 공간적 요소를 체계적으로 연구하는 학문으로, 고대부터 현재까지 이어진다.
개체군 - 생물
생물은 자기증식, 에너지 변환, 항상성 유지 능력을 갖추고 세포로 구성되며, 물질대사, 자극과 반응, 생식과 유전 등의 특징을 보이며 다양한 종으로 분류된다.
생태학 - 생물 다양성
생물 다양성은 특정 지역 내 유전자, 종, 생태계의 총체로서, 종 내, 종 간, 생태계의 다양성을 포함하는 개념이며, 식량, 의약품, 산업 원료 등 다양한 자원을 제공하고 생태계 서비스 및 문화적 가치를 지니지만, 최근 인간 활동으로 인해 급격히 감소하고 있어 보전 노력이 필요하다.
생태학 - 먹이 그물
먹이 그물은 생태계 내 생물 간의 복잡한 먹이 관계를 나타내는 연결망으로, 생태학자들은 이를 통해 생산자와 소비자 간의 에너지와 영양소 흐름을 추적하며, 먹이사슬과 영양 단계, 생태 피라미드 개념과 관련되어 생태계의 구조와 기능을 이해하는 데 중요한 역할을 한다.

로지스틱 함수
개요
함수 종류	수학, 통계학
정의	S자 모양의 곡선 또는 로지스틱 곡선을 나타내는 함수
활용 분야	인구 증가 모델링, 전염병 확산 모델링, 머신 러닝 (로지스틱 회귀)
정의
일반적인 형태	f(x) = L / (1 + e^(-k(x - x₀)))
L	곡선의 최대값
k	로지스틱 증가율 또는 곡선의 가파름
x₀	곡선의 중간점
속성
정의역	실수 전체
치역	(0, L)
대칭성	점 (x₀, L/2)에 대한 점대칭
미분	f'(x) = k * f(x) * (1 - f(x) / L)
적분	∫ f(x) dx = L * x - (L / k) * ln(1 + e^(-k(x - x₀))) + C
예시
표준 로지스틱 함수	f(x) = 1 / (1 + e^(-x))
최대값 (L)	1
증가율 (k)	1
중간점 (x₀)	0
활용
인구 모델	시간에 따른 인구 변화 예측
전염병 모델	질병 확산 예측
머신 러닝	로지스틱 회귀 모델
같이 보기
로지스틱 회귀	머신 러닝에서 사용되는 분류 알고리즘
로지스틱 지도	카오스 이론에서 사용되는 모델
곰페르츠 곡선	로지스틱 함수와 유사한 성장 모델

2. 역사

원래 로지스틱 곡선 이미지, 베르훌스트가 "로그 곡선"이라고 부른 것과 대조됨 (현대 용어로는 "지수 곡선")

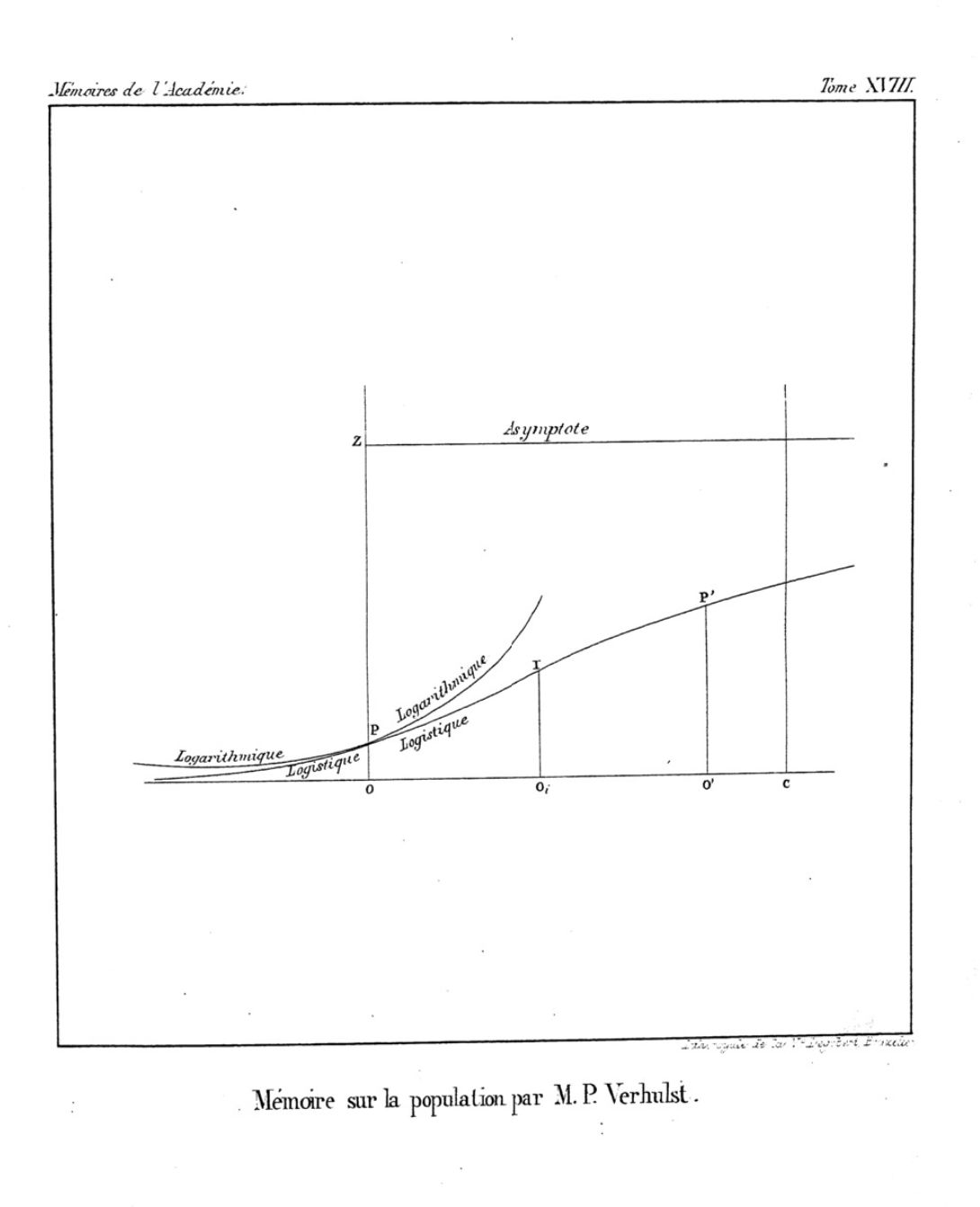
로지스틱 함수는 1838년부터 1847년까지 피에르 프랑수아 베르훌스트가 아돌프 케틀레의 지도하에 인구 성장의 모델로서 지수 성장 모델을 조정하여 고안한 것으로, 세 편의 논문으로 소개되었다.^[1] 베르훌스트는 1830년대 중반에 이 함수를 처음 고안했고, 1838년에 짧은 메모를 발표했으며,^[5] 1844년에 확장된 분석을 제시하고 그 함수에 이름을 붙였다(1845년 출판).^[6] 세 번째 논문에서는 벨기에 인구 성장에 대한 그의 모델의 보정 항을 조정했다.

성장의 초기 단계는 대략 지수적(기하학적)이며, 포화가 시작되면서 성장이 선형적(산술적)으로 둔화되고, 성숙 단계에서는 초기 단계의 역과 같이 지수적으로 감소하는 간격을 두고 한계에 접근한다.

베르훌스트는 "로지스틱"(logistique|로지스티크^프랑스어)이라는 용어의 선택을 설명하지 않았지만, 아마도 이는 '로그' 곡선과 대조하기 위한 것으로 보인다.^[7] 그는 산술적 성장과 기하학적 성장(그의 곡선을 현대 용어인 지수 곡선 대신 로그 곡선이라고 부름)에 대한 논의를 먼저 한 다음, "로지스틱 성장"은 아마도 유추에 의해 명명되었을 것이라고 추정된다. ''로지스틱''은 고대 그리스 수학의 전통적인 구분인 λογῐστῐκός|logistikós|로기스티코스^grc에서 유래했다.^[8]

고대 그리스 수학 용어에서 파생된 단어로서,^[9] 이 함수의 이름은 군사 및 관리 용어인 ''로지스틱스''와 관련이 없다.

3. 수학적 성질

로지스틱 방정식에서 시간에 따른 개체군 성장식은 다음과 같이 표현된다.

: ${dN \over dt} = rN (1- {N \over K})$

여기서 N은 개체군 크기, r은 개체당 증가율, K는 환경수용능력이다.

환경수용능력 K는 다음과 같이 정의된다.

: $K = \frac{(b_{0} - d_{0})}{(a+c)}$

여기서 $b_0$ 는 초기 개체당 출생률, $d_0$ 는 초기 개체당 사망률이며, $a$ 는 개체군 크기에 따른 개체당 출생률의 변화율, $c$ 는 개체군 크기에 따른 개체당 사망률의 변화율이다.

3. 1. 정의

표준 로지스틱 함수는

k = 1

,

x_0 = 0

,

L = 1

을 갖는 로지스틱 함수로, 다음 식을 따른다.

f(x) = \frac{1}{1 + e^{-x}} = \frac{e^x}{e^x + 1} = \frac{e^{x/2}}{e^{x/2} + e^{-x/2}}.

지수 함수

e^{-x}

의 특성상, [−6, +6]과 같은 작은 범위의 실수

x

에 대해 표준 로지스틱 함수를 계산하는 것으로 충분한 경우가 많다. 이는 표준 로지스틱 함수가 0과 1의 값에 매우 빠르게 수렴하기 때문이다.

3. 2. 대칭성

로지스틱 함수는 다음과 같은 대칭성을 갖는다.

: 1 - f(x) = f(-x)

이는 x가 작을 때 0으로부터의 성장이 x가 클 때의 극한(1)에 이르는 간격의 감소와 대칭을 이룬다는 것을 보여준다.

또한, x \mapsto f(x) - 1/2 는 기함수이다.

로지스틱 함수와 수직축에 대한 반사, f(-x)의 합은 다음과 같다.

: \frac{1}{1 + e^{-x}} + \frac{1}{1 + e^{-(-x)}} = \frac{e^x}{e^x + 1} + \frac{1}{e^x + 1} = 1

따라서 로지스틱 함수는 점 (0, 1/2)에 대해 회전 대칭이다.^[10]

3. 3. 역함수

로지스틱 함수는 자연 로짓 함수의 역함수이다.

따라서 승산의 로그를 확률로 변환한다. 두 대안의 로그 우도비로부터의 변환 또한 로지스틱 곡선의 형태를 취한다.

3. 4. 쌍곡 탄젠트 함수와의 관계

로지스틱 함수는 쌍곡 탄젠트 함수를 평행이동 및 스케일 조정하여 얻을 수 있다.

:

f(x) = \frac{1}{2} + \frac{1}{2}\tanh\left(\frac{x}{2}\right)

또는

:

\tanh(x) = 2f(2x) - 1

이는 다음 식에서 유도된다.

:

\begin{align}\tanh(x) & = \frac{e^x - e^{-x}}{e^x + e^{-x}} = \frac{e^x \cdot \left(1 - e^{-2x}\right)}{e^x \cdot \left(1 + e^{-2x}\right)} \\&= f(2x) - \frac{e^{-2x}}{1 + e^{-2x}} = f(2x) - \frac{e^{-2x} + 1 - 1}{1 + e^{-2x}} = 2f(2x) - 1.\end{align}

이러한 쌍곡 탄젠트 관계는 로지스틱 함수의 도함수를 다음과 같이 표현할 수 있게 한다.

:

\frac{d}{dx} f(x) = \frac{1}{4} \operatorname{sech}^2\left(\frac{x}{2}\right)

이는 로지스틱 함수를 로지스틱 분포와 연결한다.

3. 5. 미분

표준 로지스틱 함수는 쉽게 계산되는 도함수를 가지며, 이 도함수는 로지스틱 분포의 밀도 함수로 알려져 있다.^[11]

:

f(x) = \frac{1}{1 + e^{-x}} = \frac{e^x}{1 + e^x},

:

\begin{align}\frac{\mathrm{d}}{\mathrm{d}x}f(x) &= \frac{e^x \cdot (1 + e^x) - e^x \cdot e^x}{(1 + e^x)^2} \\&= \frac{e^{x}}{(1 + e^{x})^2} \\&= \left(\frac{e^{x}}{1 + e^{x}}\right) \left(\frac{1}{1 + e^{x}}\right) \\&= \left(\frac{e^{x}}{1 + e^{x}}\right) \left(1-\frac{e^{x}}{1 + e^{x}}\right) \\&= f(x)\left(1 - f(x)\right)\end{align}

위 식으로부터 모든 고차 도함수를 대수적으로 구할 수 있다. 예를 들어,

f'' = (1-2f)(1-f)f

이다.

표준 로지스틱 함수는 간단한 1차 비선형 상미분 방정식의 해이다.

:

\frac{d}{dx}f(x) = f(x)\big(1 - f(x)\big)

그리고 경계 조건

f(0) = 1/2

를 갖는다. 이 방정식은 로지스틱 맵의 연속 버전이다. 역 로지스틱 함수는 간단한 1차 ''선형'' 상미분 방정식의 해이다.^[11]

정성적인 행동은 위상선을 통해 쉽게 이해할 수 있다. 도함수는 함수가 1일 때 0이고, 0과 1 사이의

f

에 대해 양수이며, 1보다 크거나 0보다 작은

f

에 대해 음수이다(음의 개체수는 일반적으로 물리적 모델과 일치하지 않음). 이는 0에서 불안정한 평형 상태를, 1에서 안정적인 평형 상태를 생성하므로 0보다 크고 1보다 작은 모든 함수 값에 대해 1로 증가한다.

로지스틱 방정식은 베르누이 미분 방정식의 특수한 경우이며 다음과 같은 해를 갖는다.

:

f(x) = \frac{e^x}{e^x + C}.

적분 상수

C = 1

을 선택하면 로지스틱 곡선의 정의에 대한 또 다른 잘 알려진 형태가 얻어진다.

:

f(x) = \frac{e^x}{e^x + 1} = \frac{1}{1 + e^{-x}}.

해석적 해에서 볼 수 있듯이 로지스틱 곡선은 음의 인수에 대해 초기 지수 성장을 보이며, 이는 0 근처의 인수에 대해 기울기 1/4의 선형 성장에 도달한 다음 지수적으로 감소하는 간격으로 1에 접근한다.

위에서 파생된 미분 방정식은

x > 0

에 대해서만 시그모이드 함수를 모델링하는 일반적인 미분 방정식의 특수한 경우이다. 많은 모델링 응용 분야에서, 더 ''일반적인 형태''^[12]

:

\frac{df(x)}{dx} = \frac{k}{a} f(x)\big(a - f(x)\big), \quad f(0) = \frac a {1 + e^{kr}}

가 바람직할 수 있다. 해는 이동 및 스케일된 시그모이드

aS\big(k(x - r)\big)

이다.

3. 6. 적분

표준 로지스틱 함수의 부정 적분은

u = 1 + e^x

를 치환 적분하여 계산할 수 있다.

f(x) = \frac{e^x}{1 + e^x} = \frac{u'}{u},

따라서 (적분 상수는 생략)

\int \frac{e^x}{1 + e^x}\,dx = \int \frac{1}{u}\,du = \ln u = \ln (1 + e^x).

인공 신경망에서 이는 ''소프트플러스 함수''라고 알려져 있으며 (스케일링을 통해) 램프 함수의 부드러운 근사이고, 로지스틱 함수(스케일링을 통해)가 헤비사이드 계단 함수의 부드러운 근사인 것과 같다.

로지스틱 함수의 생태학적 형태의 부정적분은

u = K + P_0 \left( e^{rt} - 1\right)

의 치환 적분을 사용하여 계산할 수 있으며,

du = r P_0 e^{rt} dt

이기 때문이다.

\int \frac{K P_0 e^{rt}}{K + P_0 \left( e^{rt} - 1\right)}\,dt = \int \frac{K}{r} \frac{1}{u}\,du = \frac{K}{r} \ln u + C = \frac{K}{r} \ln \left(K + P_0 (e^{rt} - 1) \right) + C

4. 응용

로지스틱 함수는 다양한 분야에서 응용된다. 용량 L=1일 때 로지스틱 함수 값은 (0, 1) 범위에 있으며, 확률 p로 해석될 수 있다. 입력 x는 첫 번째 대안에 대한 로그 오즈(log odds)로, 로짓(로지스틱 단위)으로 측정된다. e^x^영어는 첫 번째 사건에 대한 오즈(odds)를 나타낸다. 이러한 해석은 소프트맥스 함수로 일반화될 수 있다.

생태학: 인구 성장 모델에 사용된다. 피에르-프랑수아 베르훌스트가 처음 제시했으며, 맬서스 성장 모델을 참고하여 만들어졌다.
통계학 및 머신 러닝: 로지스틱 회귀, 로그 선형 모델, 다항 로지스틱 회귀, 문항 반응 이론의 라쉬 모형, 인공 신경망의 활성화 함수 등에 쓰인다.
의학: 종양 성장 및 전염병 확산 모델에 사용된다.
화학: 자가 촉매 반응 모델링에 사용된다.
물리학: 페르미-디랙 분포를 설명한다.
광학: 신기루 현상을 모델링한다.
언어학: 언어 변화를 모델링한다.
농업: 작물 반응을 모델링한다.
경제학 및 사회학: 혁신 확산을 모델링한다. 가브리엘 타르드는 저서 『모방의 법칙』(1890)에서 모방을 통한 새로운 아이디어 확산 과정을 설명했다.
순차 분석: Link^[38]는 양의 경계에 처음 도달하거나 초과할 확률을 로지스틱 함수로 유도했다.^[39]

4. 1. 생태학: 개체군 성장 모델

로지스틱형 개체군 성장 모델에서 시간에 따른 개체군 성장 식은 다음과 같이 표현된다.

:

{dN \over dt} = rN (1- {N \over K})

여기서 N은 개체군 크기, r은 개체당 증가율, K는 환경수용능력이다.

환경수용능력 K는 다음과 같이 정의된다.

:

K = \frac{(b_{0} - d_{0})}{(a+c)}

여기서

b_0

는 초기 개체당 출생률,

d_0

는 초기 개체당 사망률이며,

a

는 개체군 크기에 따른 개체당 출생률의 변화율,

c

는 개체군 크기에 따른 개체당 사망률의 변화율이다.

로지스틱 방정식의 전형적인 응용은 인구 성장의 일반적인 모델로, 1838년 피에르-프랑수아 베르훌스트에 의해 제시되었다.^[1] 번식률은 기존 인구와 가용한 자원의 양에 모두 비례하며, 다른 모든 조건은 동일하다. 베르훌스트는 토머스 맬서스의 ''인구론''을 읽은 후 맬서스 성장 모델을 참고하여 생물학적 인구의 자기 제한적 성장을 설명하기 위해 자신의 로지스틱 방정식을 도출했다. 이 방정식은 1911년 앤더슨 그레이 맥켄드릭에 의해 국물 속 세균의 성장에 대해 재발견되었고 비선형 매개변수 추정 기술을 사용하여 실험적으로 테스트되었다.^[13] 1920년 존스 홉킨스 대학교의 레이먼드 펄 (1879–1940)과 로웰 리드 (1888–1966)에 의해 재발견된 후, 때때로 ''베르훌스트-펄 방정식''이라고도 불린다.^[14] 알프레드 J. 로트카는 1925년에 이 방정식을 다시 도출하여 ''인구 성장 법칙''이라고 불렀다.

P

를 인구 크기(생태학에서는 종종

N

을 대신 사용함)로,

t

를 시간으로 나타내면, 이 모델은 다음의 미분 방정식으로 공식화된다.

:

\frac{dP}{dt}=r P \left(1 - \frac{P}{K}\right),

여기서 상수

r

은 인구 성장률을 정의하고,

K

는 최대 수용력을 나타낸다.

이 방정식에서 초기, 방해받지 않는 성장률은 첫 번째 항

+rP

에 의해 모델링된다. 비율

r

의 값은 단위 시간당 인구

P

의 비례적 증가를 나타낸다. 나중에, 인구가 증가함에 따라, 두 번째 항의 절대값 (

-r P^2 / K

)은 인구

P

의 일부 구성원이 음식이나 생활 공간과 같은 중요한 자원을 놓고 경쟁함으로써 서로 간섭함에 따라 첫 번째 항과 거의 같아진다. 이 적대적인 효과를 ''병목 현상''이라고 하며, 매개변수

K

의 값으로 모델링된다. 경쟁은 결합된 성장률을 감소시키고, 결국

P

의 값이 더 이상 증가하지 않게 된다 (이를 인구의 ''성숙''이라고 부른다).

이 방정식의 해 (초기 인구를

P_0

로)는 다음과 같다.

:

P(t) = \frac{K P_0 e^{rt}}{K + P_0 \left( e^{rt} - 1\right)} = \frac{K}{1+\left(\frac{K-P_0}{P_0}\right)e^{-rt}},

여기서,

:

\lim_{t\to\infty} P(t) = K,

여기서

K

는

P

의 극한 값이며, 인구가 무한한 시간 동안 도달할 수 있는 가장 높은 값 (또는 유한한 시간 내에 근접하게 도달할 수 있는 값)이다. 최대 수용력은 초기 값

P(0) > 0

과

P(0) > K

의 경우에도 비례하여 도달된다.

생태학에서 종은 때때로

r

-전략가 또는

K

-전략가로 언급되며, 이는 그들의 생물학적 생활사 전략을 형성한 자연 선택 과정에 따라 달라진다.

차원 분석을 통해 변수 차원을 선택하여

n

이 최대 수용력 단위로 인구를 측정하고,

\tau

가

1/r

단위로 시간을 측정하면, 다음과 같은 무차원 미분 방정식을 얻는다.

:

\frac{dn}{d\tau} =  n (1-n).

4. 2. 통계학 및 머신 러닝

로지스틱 함수는 용량 L=1 일 때, (0, 1) 범위의 값을 가지며, 이는 확률 p로 해석될 수 있다. 입력 x는 첫 번째 대안에 대한 로그 오즈(log odds)로, 로짓(로지스틱 단위)로 측정된다. e^x^영어는 첫 번째 사건에 대한 오즈(odds)를 나타낸다.

이러한 해석은 두 입력 x_0^영어와 x_1^영어의 관점에서 대칭적으로 구성될 수 있으며, 이는 소프트맥스 함수로 일반화된다.

로지스틱 함수는 통계학에서 여러 역할로 사용된다. 예를 들어, 로지스틱 분포의 누적 분포 함수이며, 엘로 평점 시스템에서 체스 선수가 상대방을 이길 확률을 모델링하는 데 사용된다.

로지스틱 회귀에서 로지스틱 함수는 사건의 확률이 설명 변수에 의해 어떻게 영향을 받는지 모델링하는 데 사용된다. 예를 들어 다음과 같은 모델을 사용할 수 있다.

:

p = f(a + bx)

여기서 x는 설명 변수, a와 b는 모델 매개변수, f는 표준 로지스틱 함수이다.

로지스틱 회귀 및 기타 로그 선형 모델은 머신 러닝에서도 사용된다. 로지스틱 함수를 여러 입력으로 일반화한 것은 소프트맥스 활성화 함수이며, 이는 다항 로지스틱 회귀에 사용된다.

로지스틱 함수의 또 다른 응용은 문항 반응 이론의 라쉬 모형이다. 라쉬 모형은 정답과 오답으로 분류된 응답을 기반으로 객체 또는 사람의 위치를 추정하는 데 기초를 형성한다.

로지스틱 함수는 인공 신경망에서 모델에 비선형성을 도입하거나 신호를 특정 구간 내로 고정하기 위해 자주 사용된다. 인공 뉴런은 입력 신호의 선형 결합을 계산하고, 그 결과에 제한된 로지스틱 함수를 활성화 함수로 적용한다. 이 모델은 고전적인 퍼셉트론의 "매끄러운" 변형으로 볼 수 있다.

4. 3. 의학: 종양 성장 및 전염병 모델

로지스틱 함수는 의학 분야에서 종양의 성장을 모델링하는 데 사용될 수 있다. 이는 생태학에서 사용되는 로지스틱 미분 방정식의 확장으로 볼 수 있다. 종양의 크기를

X(t)

라고 할 때, 그 성장 역학은 다음과 같이 표현된다.

X' = r\left(1 - \frac X K \right)X

여기서

F(X)

는 종양의 증식률을 나타내며,

F'(X) \le 0

이다.

화학 요법을 통해 치료를 시작하면, 방정식은 다음과 같이 수정될 수 있다.

X' = r\left(1 - \frac X K \right)X - c(t) X

여기서

c(t)

는 치료로 인한 사망률을 나타낸다. 장기간의 치료에서

c(t)

는 주기 함수(주기

T

) 또는 상수 함수로 모델링될 수 있으며, 평균 치료 유발 사망률이 기준선 증식률보다 크면 질병이 근절된다는 결론을 얻을 수 있다.

\frac 1 T \int_0^T c(t)\, dt > r \to \lim_{t \to +\infty} x(t) = 0

하지만, 이는 성장과 치료를 단순화한 모델이며, 복제 저항과 같은 현상은 고려하지 않았다.

로지스틱 함수는 전염병 확산 모델에도 사용된다. 면역력이 없는 새로운 전염병은 초기 단계에서 기하급수적으로 확산되는 경향이 있다. 코로나19를 유발하는 SARS-CoV-2 바이러스는 2020년 초 여러 국가에서 감염 초기에 이러한 기하급수적 증가를 보였다.^[19] 그러나 감염 취약 숙주 부족이나 사회적 거리두기와 같은 요인으로 인해, 유행 곡선은 선형화되고 결국 최대 한계에 도달한다.^[20]

로지스틱 함수나 곰페르츠 함수와 같은 관련 함수들은 초기 기하급수적 증가와 함께 유행병이 둔화되는 현상을 잘 설명하기 때문에, 일반적으로 설명적 또는 현상학적 방식으로 사용된다. 실제 유행병 모델은 유행병의 역학을 기반으로 설명을 공식화하려고 하지만, 로지스틱 해를 산출하는 몇 가지 간단한 모델도 개발되었다.^[21]^[22]^[23]

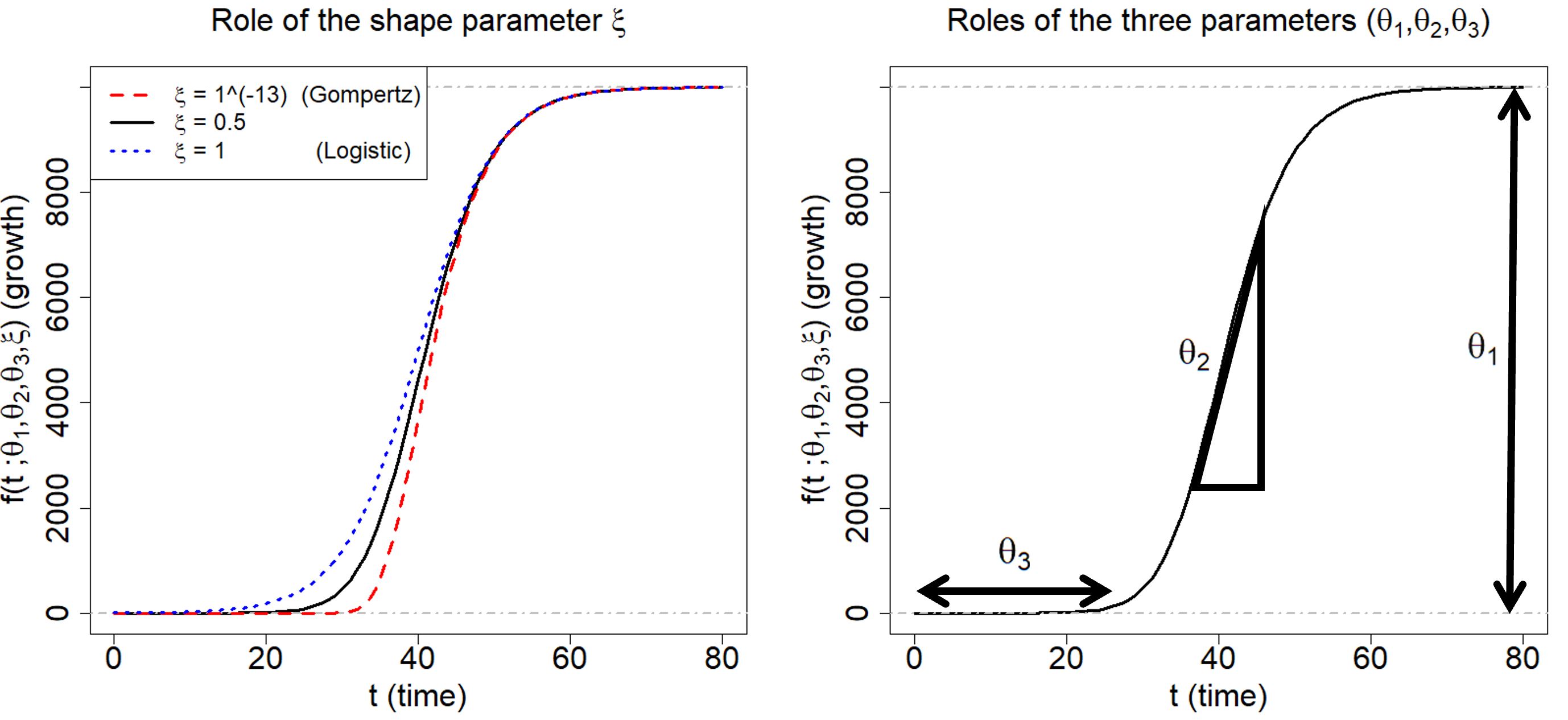
일반화 로지스틱 함수(리처드 성장 곡선)는 코로나19 발병 초기 단계를 모델링하는 데 사용되었다.^[24] 이 함수는 누적 감염자 수, 즉 '감염 궤적'을 나타내는 데 사용된다. 일반화 로지스틱 함수의 한 가지 형태는 다음과 같다.

f(t ; \theta_1,\theta_2,\theta_3, \xi) = \frac{\theta_1}{[1 + \xi \exp (-\theta_2 \cdot (t - \theta_3) ) ]^{1/\xi}}

여기서

\theta_1,\theta_2,\theta_3

는 실수이고,

\xi

는 양의 실수이다.

\xi = 1

이면 로지스틱 함수,

\xi

가 0에 가까워지면 곰페르츠 함수로 수렴한다. 전염병 모델링에서

\theta_1

,

\theta_2

,

\theta_3

는 각각 최종 유행 규모, 감염률, 지연 단계를 나타낸다.

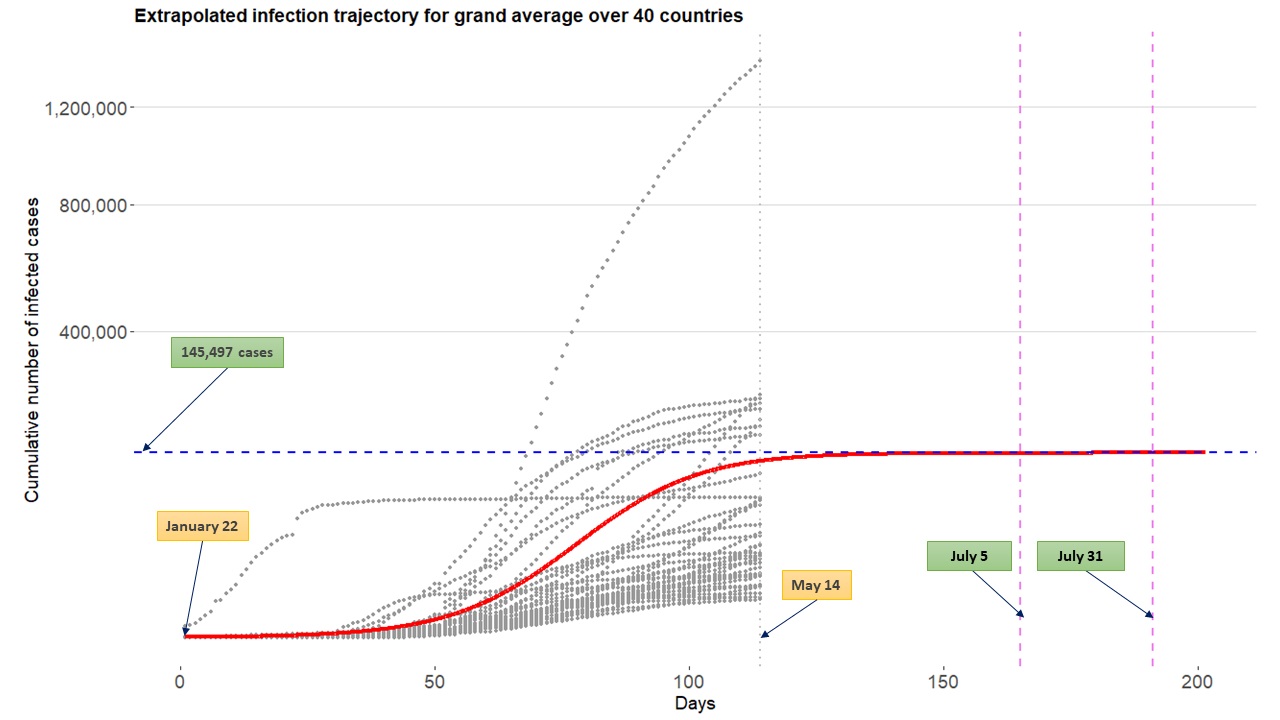
5월 14일까지 코로나19의 심각한 영향을 받은 40개 국가의 추정 감염 궤적 및 전체 (인구) 평균

일반화 로지스틱 함수와 같은 성장 함수를 사용하면, 서로 다른 지역의 정보를 묶어 다단계 모델 프레임워크에 적용하기 쉽다는 장점이 있다.

4. 4. 화학: 자가 촉매 반응

자가 촉매 반응에서 반응물과 생성물의 농도는 로지스틱 함수를 따른다. 백금족 금속이 없는(PGM-free) 연료 전지 음극의 산소 환원 반응(ORR) 촉매의 열화는 로지스틱 감소 함수를 따르며,^[25] 이는 자가 촉매 열화 메커니즘을 시사한다.

4. 5. 물리학: 페르미-디랙 분포

로지스틱 함수는 열적 평형 상태에 있는 시스템에서 에너지 상태에 대한 페르미온의 통계적 분포를 결정한다. 특히, 페르미-디랙 통계에 따라 각 가능한 에너지 수준이 페르미온에 의해 점유될 확률의 분포이다.^[1]

4. 6. 광학: 신기루

로지스틱 함수는 광학에서도 응용되며, 특히 신기루와 같은 현상을 모델링하는 데 사용된다. 확산으로 인한 온도 또는 농도 기울기의 존재와 중력과의 균형 같은 특정 조건에서 로지스틱 곡선 거동이 나타날 수 있다.^[26]^[27]

신기루는 거리에 따른 물질의 밀도/농도와 관련된 굴절률을 수정하는 온도 기울기의 결과로 발생하며, 농도 기울기로 인해 굴절률 기울기가 있는 유체를 사용하여 모델링할 수 있다. 이 메커니즘은 제한된 개체군 성장 모델과 동일시될 수 있으며, 여기서 농축된 영역은 중력과의 평형을 추구하면서 낮은 농도 영역으로 확산하려고 시도하여 로지스틱 함수 곡선을 생성한다.^[26]

4. 7. 언어학: 언어 변화

언어학에서 로지스틱 함수는 언어 변화를 모델링하는 데 사용될 수 있다.^[28] 처음에는 미미했던 혁신이 시간이 지남에 따라 더 빠르게 확산되기 시작하고, 보편적으로 채택됨에 따라 더 느리게 확산된다.

4. 8. 농업: 작물 반응 모델링

로지스틱 S-곡선은 생장 인자의 변화에 대한 작물 반응을 모델링하는 데 사용될 수 있다. 반응 함수에는 ''양의'' 생장 곡선과 ''음의'' 생장 곡선 두 가지 유형이 있다. 예를 들어, 작물 수확량은 특정 수준까지 생장 인자 값이 증가함에 따라 ''증가''할 수 있다(양의 함수). 또는 생장 인자 값 증가에 따라 ''감소''할 수 있는데(음의 생장 인자로 인한 음의 함수), 이 경우에는 ''반전된'' S-곡선이 필요하다.^[29]^[30]

4. 9. 경제학 및 사회학: 혁신 확산

가브리엘 타르드는 저서 『모방의 법칙』(1890)에서 모방의 연쇄를 통해 새로운 아이디어가 등장하고 확산되는 과정을 설명한다. 타르드는 혁신 확산의 세 가지 주요 단계를 다음과 같이 제시했다.

1. 아이디어가 적대적인 환경 속에서 반대되는 습관과 신념과 싸워야 하는 어려운 시작

2.

f(x)=2^x

로 표현되는 아이디어가 제대로 지수적으로 도약하는 단계

3.

f(x)=\log(x)

로 표현되는 로그 단계. 아이디어의 추진력이 점차 둔화되는 시기에 해당하며, 동시에 새로운 반대 아이디어가 나타나 혁신의 진행이 중단되거나 안정화되어 점근선에 접근

주권 국가에서 하위 국가 단위(구성 국가 또는 도시)는 프로젝트 자금 조달을 위해 대출을 사용할 수 있다. 그러나 이 자금 조달원은 엄격한 법적 규칙뿐만 아니라 경제적 희소성 제약, 특히 은행이 대출할 수 있는 자원(은행의 자기자본 또는 바젤 III 한도)의 제약을 받는다. 이러한 제한은 포화 수준을 나타내며, 돈을 위한 경제적 경쟁에서 지수적인 경쟁과 함께 공공 재정에서 신용 요청이 확산되고, 이에 대한 총체적인 국가적 반응은 시그모이드 곡선을 나타낸다.^[31]

역사적으로, 새로운 제품이 출시되면 품질을 극적으로 개선하고 비용을 절감하기 위한 막대한 양의 연구 개발이 이루어진다. 이는 산업의 급속한 성장을 이끌어낸다. 더 유명한 예로는 철도, 백열전구, 전기 공급, 자동차, 항공 여행 등이 있다. 결국, 극적인 개선과 비용 절감의 기회가 소진되고, 제품 또는 프로세스가 널리 사용되어 잠재적인 신규 고객이 거의 남지 않으며, 시장이 포화 상태가 된다.

국제 응용 시스템 분석 연구소(IIASA)의 여러 연구자들의 논문은 다양한 혁신, 인프라 및 에너지원 대체 확산, 경제에서 노동의 역할, 그리고 장기 경제 사이클을 다루고 있다. 장기 경제 사이클은 로버트 에이어스(1989)에 의해 연구되었다.^[32] 체사레 마르케티는 콘드라티예프 파동과 혁신의 확산에 대해 발표했다.^[33]^[34] 아르놀프 그뤼블러의 저서(1990)는 운하, 철도, 고속도로 및 항공을 포함한 인프라의 확산에 대한 상세한 설명을 제공하며, 이러한 확산이 로지스틱 형태의 곡선을 따른다는 것을 보여준다.^[35]

칼로타 페레즈는 로지스틱 곡선을 사용하여 기술 시대의 시작을 '돌입', 상승을 '광란', 빠른 확장을 '시너지', 완성을 '성숙'이라는 라벨로 하여 장기 콘드라티예프 파동 경기 사이클을 설명했다.^[36]

로지스틱 성장 회귀는 데이터가 성장 과정의 변곡점 근처까지만 사용 가능한 경우 상당한 불확실성을 갖는다. 이러한 조건에서 변곡점이 발생할 높이를 추정하는 것은 시스템의 최대 수용력(K)과 유사한 불확실성을 가질 수 있다.

이러한 불확실성을 완화하는 방법은 대리 로지스틱 성장 과정을 통해 최대 수용력을 참조점으로 사용하는 것이다.^[37] 이러한 제약을 통합함으로써 K가 단지 2배의 인자 내의 추정치일지라도 회귀가 안정화되어 예측 매개변수의 정확도를 향상시키고 불확실성을 줄인다. 이러한 접근 방식은 경제학 및 생물학과 같은 분야에서 유사한 대리 시스템 또는 집단을 분석에 적용할 수 있는 경우에 적용할 수 있다.

4. 10. 순차 분석

Link^[38]는 발트의 순차 분석 이론을 확장하여, 무작위 변수의 분포에 관계없이, 양 또는 음의 경계에 처음 도달하거나 초과할 때까지 변수를 누적하는 방법을 개발했다. Link^[39]는 양의 경계에 처음 도달하거나 초과할 확률을

1/(1+e^{-\theta A})

, 즉 로지스틱 함수로 유도했다. 이는 로지스틱 함수가 확률 과정을 기초로 할 수 있다는 최초의 증명이다. Link^[40]는 이 확률과 경계에서의 흡수 시간 사이의 새롭게 유도된 관계와 함께, 한 세기 동안의 "로지스틱" 실험 결과의 예를 제공한다.

참조

_[1] 논문 Notice sur la loi que la population poursuit dans son accroissement https://books.google[...] 2014-12-03
_[2] 웹사이트 Sigmoid — PyTorch 1.10.1 documentation https://pytorch.org/[...]
_[3] 문서 expit documentation for R's clusterPower package http://www.inside-r.[...]
_[4] 웹사이트 Scipy.special.expit — SciPy v1.7.1 Manual https://docs.scipy.o[...]
_[5] 논문 Recherches mathématiques sur la loi d'accroissement de la population http://gdz.sub.uni-g[...] 2013-02-18
_[6] 논문 Deuxième mémoire sur la loi d'accroissement de la population http://gdz.sub.uni-g[...] 2013-02-18
_[7] 논문 Math-alive! using original sources to teach mathematics in social context https://www.research[...]
_[8] 논문 Ancient logistics – historical timeline and etymology http://pdfs.semantic[...]
_[9] 서적 Tableau Analytique des principales combinaisons De La Guerre, Et De Leurs Rapports Avec La Politique Des États: Pour Servir D'Introduction Au Traité Des Grandes Opérations Militaires
_[10] 서적 Neural Networks – A Systematic Introduction http://page.mi.fu-be[...] 2016-10-15
_[11] 논문 Bayesian Sigmoid-Type Time Series Forecasting with Missing Data for Greenhouse Crops 2020-06-07
_[12] 문서 Sigmoid functions: some approximation and modelling aspects LAP LAMBERT Academic Publishing, Saarbrucken
_[13] 논문 XLV.—The Rate of Multiplication of Micro-organisms: A Mathematical Study https://zenodo.org/r[...] 1912-01
_[14] 뉴스 On the Rate of Growth of the Population of the United States http://math.bu.edu/p[...] 1920-06
_[15] 논문 Linear and nonlinear waves 2009
_[16] 논문 Punctuated evolution due to delayed carrying capacity
_[17] 문서
_[18] 서적 Neural Networks: Tricks of the trade Springer
_[19] 웹사이트 COVID-19 CORONAVIRUS PANDEMIC https://www.worldome[...]
_[20] arXiv Using generalized logistics regression to forecast population infected by Covid-19
_[21] 논문 Estimation of COVID-19 dynamics "on a back-of-envelope": Does the simplest SIR model provide quantitative parameters and predictions? 2020-06
_[22] medRxiv A Logistic Curve in the SIR Model and Its Application to Deaths by COVID-19 in Japan 2020-06
_[23] arXiv Modified SIR Model Yielding a Logistic Solution
_[24] 논문 Estimation of COVID-19 spread curves integrating global data and borrowing information
_[25] 논문 Kinetic Models for the Degradation Mechanisms of PGM-Free ORR Catalysts https://www.osti.gov[...] 2018-07-13
_[26] 논문 Measuring refractive index gradient of sugar solution 2021-05-24
_[27] 논문 Mirages in a bottle https://iopscience.i[...] 2009
_[28] 문서
_[29] 문서 Collection of data on crop production and depth of the water table in the soil of various authors https://www.waterlog[...]
_[30] 문서 Collection of data on crop production and soil salinity of various authors https://www.waterlog[...]
_[31] 논문 Is the public sector of your country a diffusion borrower? Empirical evidence from Brazil 2017-10-05
_[32] 웹사이트 Technological Transformations and Long Waves http://www.iiasa.ac.[...] 2010-11-06
_[33] 웹사이트 Pervasive Long Waves: Is Society Cyclotymic http://www.agci.org/[...]
_[34] 웹사이트 Kondratiev Revisited-After One Cycle http://www.cesaremar[...] 2010-11-06
_[35] 서적 The Rise and Fall of Infrastructures: Dynamics of Evolution and Technological Change in Transport http://pure.iiasa.ac[...] Physica-Verlag
_[36] 서적 Technological Revolutions and Financial Capital: The Dynamics of Bubbles and Golden Ages https://archive.org/[...] Edward Elgar Publishing Limited
_[37] 간행물 Uncertainty Reduction in Logistic Growth Regression Using Surrogate Systems Carrying Capacities: a COVID-19 Case Study
_[38] 간행물 A sequential theory of psychological discrimination 1975
_[39] 서적 Attention and Performance VII Taylor & Francis 1978
_[40] 서적 The wave theory of difference and similarity Taylor and Francis

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com