정신물리학
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
정신물리학은 물리적 자극과 감각 사이의 관계를 연구하는 학문으로, 1860년 구스타프 페히너에 의해 시작되었다. 페히너는 베버의 연구를 바탕으로 베버-페히너의 법칙을 확립했으며, 스탠리 스미스 스티븐스는 스티븐스의 멱법칙을 제안했다. 정신물리학은 시각, 청각, 미각 등 다양한 감각 영역에서 절대 역치, 차이 역치, 척도 등을 연구하며, 실험 방법으로는 한계법, 고정 자극법, 조정법 등이 사용된다. 이러한 연구는 심리음향학, 인지심리학, 인간공학 등 다양한 분야에 응용된다.
더 읽어볼만한 페이지
- 정신물리학 - 탐지 이론
탐지 이론은 불확실한 상황에서 신호를 탐지하고 판단하는 과정을 분석하는 이론으로, 관찰자의 민감도, 편향, 의사 결정 기준이 중요한 역할을 하며 다양한 분야에서 활용된다. - 정신물리학 - 스트루프 효과
스트루프 효과는 단어의 의미와 잉크 색상이 일치하지 않을 때 색상 식별에 시간이 더 걸리는 현상이며, 주의력, 인지 기능 등을 평가하는 데 사용된다. - 신경과학 - 인공 일반 지능
인공 일반 지능(AGI)은 추론, 지식 표현, 학습 등의 능력을 갖춘 인공지능 시스템을 의미하며, 기아와 빈곤 해결 등의 이점을 제공하지만 통제력 상실과 같은 위험도 존재한다. - 신경과학 - 계산신경과학
계산신경과학은 컴퓨터 과학과 신경과학의 융합 분야로, 뇌의 정보 처리 과정을 계산 모델로 연구하며, 뇌 기능 설명, 뉴런 및 신경망 모델링, 인공지능 활용 비교 연구, 계산 임상 신경과학 발전 등을 포함한다.
| 정신물리학 | |
|---|---|
| 개요 | |
| 학문 분야 | 심리학, 생리학 |
| 하위 분야 | 감각, 지각 |
| 관련 학문 | 신경과학, 인지심리학 |
| 측정 방법 | 정신물리학적 방법 |
| 주요 연구 | 절대 식역, 차이 식역, 척도 구성 |
| 역사 | |
| 창시자 | 에른스트 하인리히 베버, 구스타프 테오도르 페히너 |
| 주요 발전 | 신호 감지 이론, 스티븐스의 멱법칙 |
| 주요 개념 | |
| 감각 | 물리적 자극에 대한 감각 기관의 반응 |
| 지각 | 감각 정보를 해석하고 의미를 부여하는 과정 |
| 식역 | 감각을 느낄 수 있는 최소한의 자극 강도 (절대 식역) 또는 자극 간의 최소한의 차이 (차이 식역) |
| 감각 척도 | 감각의 강도를 측정하는 척도 |
| 정신물리학적 함수 | 자극의 물리적 강도와 주관적인 감각 강도 간의 관계를 나타내는 함수 |
| 응용 분야 | |
| 인간 공학 | 제품 및 시스템 설계 시 인간의 감각 및 지각 능력을 고려 |
| 광고 | 소비자의 감각적 경험을 자극하여 광고 효과를 높임 |
| 의학 | 감각 장애 진단 및 치료, 통증 연구 |
| 예술 | 시각 및 청각 예술 작품 제작 시 감각적 효과를 고려 |
| 주요 정신물리학자 | |
| 이름 | 구스타프 테오도르 페히너 |
| 업적 | 정신물리학의 창시자, 페히너의 법칙 제안 |
| 이름 | 에른스트 하인리히 베버 |
| 업적 | 베버의 법칙 발견 |
| 이름 | 스탠리 스미스 스티븐스 |
| 업적 | 스티븐스의 멱법칙 제안 |
| 이름 | 윌리엄 앨런 턴불 |
| 업적 | 신호 감지 이론 발전 |
2. 역사
정신물리학은 1860년 구스타프 테오도어 페히너가 《정신물리학의 요소》(Elemente der Psychophysik)를 출판하면서 시작되었다.[32] 페히너는 '정신물리학'이라는 용어를 처음 사용하고, 물리적 자극과 감각 사이의 관계를 연구했다. 에른스트 하인리히 베버의 연구에서 영감을 받아 베버-페히너의 법칙을 확립했다. 베버와 페히너의 연구는 빌헬름 분트가 라이프치히에 최초의 심리학 연구소(실험 심리학 연구소)를 설립하는 데 영향을 주었다.[5][6][7]
찰스 샌더스 퍼스는 조셉 야스트로와 함께 페히너의 발견을 확장하고 무게 지각 역치 추정치를 기각했다. 퍼스-야스트로 실험은 무작위 실험과 블라인드 반복 측정 설계를 통해 이루어졌다.[8][9][10][11] 스탠리 스미스 스티븐스는 멱법칙 아이디어를 부활시키고, 스티븐스의 멱법칙을 제안했다.
중세 과학자 알하젠을 정신물리학의 창시자로 보는 견해도 있으나,[13] 정량적 기법 사용 증거는 부족하여 반박되었다.[14]
2. 1. 주요 학자
구스타프 테오도어 페히너는 정신물리학의 창시자로 여겨진다. 1860년, 그는 ''정신물리학의 원리(Elemente der Psychophysik)''를 출판하여 정신물리학의 많은 방법과 이론의 기초를 닦았다.[5] 그는 물리적 자극과 감각, 의식 사이의 관계를 연구하기 위해 "정신물리학"이라는 용어를 사용했다. 페히너는 페히너 척도로 알려진 로그 척도를 도출했다.[6][7]에른스트 하인리히 베버는 페히너에게 영감을 준 생리학자이다. 베버는 최소 식별 가능한 차이(jnd)에 대한 연구를 통해, 자극의 변화를 감지하기 위해서는 원래 자극의 일정 비율 이상이 변화해야 한다는 베버의 법칙을 발견했다.[6][7]
빌헬름 분트는 라이프치히에 최초의 심리학 연구소를 설립하여 실험 심리학의 아버지로 불린다. 베버와 페히너의 연구는 심리학을 과학으로 발전시키는 데 중요한 역할을 했으며, 분트의 연구소 설립에 영향을 미쳤다.
찰스 S. 퍼스는 페히너의 연구를 확장하고, 조셉 야스트로와 함께 무게 지각 역치에 대한 연구를 진행했다. 이들은 무작위 실험과 블라인드 반복 측정 설계를 도입하여, 페히너의 추정치와 다른 결과를 얻었다.[8][9][10][11] 퍼스의 실험은 심리학 및 교육 분야의 다른 연구자들에게 영감을 주어, 무작위 실험 연구 전통을 발전시켰다.[8][9][10][11]
조셉 야스트로는 퍼스와 함께 무게 지각 역치 연구에 참여한 실험 심리학자이다.
스탠리 스미스 스티븐스는 스티븐스의 멱법칙을 제안하고 크기 추정법을 개발한 심리학자이다. 그는 페히너의 로그-선형 함수와 대조되는 멱법칙 아이디어를 부활시켰다.
3. 정의
정신물리학은 하나 혹은 그 이상의 차원에서 변화하는 자극에 대한 실험 대상의 경험이나 체계적인 행동에 미치는 영향에 대한 지각 과정의 분석 연구이다.[31] 물리적 자극과 심리적 경험 사이의 양적 관계를 체계적으로 연구한다.
구스타프 테오도어 페히너가 1860년 《정신물리학의 요소》(Elemente der Psychophysik)를 발표하면서 정신물리학이 시작되었다.[32] 그는 '정신물리학'이라는 용어를 처음 사용하고 마음 연구와 관련된 많은 이론을 연구하였다. 이후 에른스트 하인리히 베버와 빌헬름 분트와 같은 학자들에게 큰 영향을 주었다. 정신물리학 분야의 대표적 이론으로 신호탐지이론이 있다.
페히너는 물리적 자극과 감각(Empfindungen)과 같은 의식 내용 사이의 관계를 연구하기 위해 "정신물리학"이라는 용어를 만들었다. 그는 물리학자이자 철학자로서 물질과 정신을 연결하고, 공개적으로 관찰 가능한 세계와 사람이 사적으로 경험하는 인상을 연결하는 방법을 개발하는 것을 목표로 했다. 그의 아이디어는 1830년대 초 에른스트 하인리히 베버가 라이프치히에서 얻은 촉각과 빛에 대한 실험 결과에서 영감을 받았다.[6][7] 베버는 중간 강도 자극의 최소 식별 가능한 차이(최소 식별 차이; jnd)에 대해 연구했는데, 이는 기준 강도의 일정한 비율이라는 것을 보여주었고, 페히너는 이를 베버의 법칙이라고 불렀다. 이를 통해 페히너는 오늘날 페히너 척도로 알려진 유명한 로그 척도를 도출했다.
베버와 페히너의 연구는 심리학을 과학으로 만드는 기초 중 하나가 되었고, 빌헬름 분트는 라이프치히에 최초의 심리학 연구소를 설립했다(실험 심리학 연구소). 페히너의 연구는 내성주의적 접근 방식(의식 과학으로서의 심리학)을 체계화했는데, 이는 언어적 반응조차도 자극만큼 물리적인 행동주의적 접근 방식과 경쟁해야 했다.
페히너의 연구는 찰스 S. 퍼스와 그의 제자 조셉 야스트로에 의해 연구되고 확장되었다. 퍼스와 야스트로는 페히너의 경험적 발견을 대체로 확인했지만, 모두 그런 것은 아니었다. 특히 퍼스와 야스트로의 고전적인 실험은 무게에 대한 지각 역치에 대한 페히너의 추정치를 기각했다. 그들의 실험에서, 퍼스와 야스트로는 실제로 무작위 실험을 발명했다. 그들은 자원 봉사자들을 무작위로 배정하여 블라인드 반복 측정 설계를 통해 무게를 구별하는 능력을 평가했다.[8][9][10][11] 그들의 결과에 기초하여 그들은 기본 함수가 연속적이며 물리적 크기의 차이가 감지되지 않는 역치가 없다고 주장했다. 퍼스의 실험은 심리학 및 교육 분야의 다른 연구자들에게 영감을 주었고, 1900년대에 실험실에서 무작위 실험을 하고 전문적인 교과서를 출판하는 연구 전통을 발전시켰다.[8][9][10][11]
퍼스-야스트로 실험은 퍼스가 실용주의 프로그램을 인간 지각에 적용하는 과정의 일부로 수행되었으며, 빛의 지각 등에 대한 다른 연구가 진행되었다.[12] 야스트로는 다음과 같이 요약했다.
> 퍼스 씨의 논리학 강좌는 저에게 지적 근육에 대한 최초의 진정한 경험을 안겨주었습니다. 스탠리 홀에 의해 심리학 연구소가 설립되자마자 저는 즉시 심리학 실험실로 갔지만, 저에게 심리학적 문제를 다루는 첫 번째 훈련을 제공하고, 당시 실험 습관에 거의 익숙하지 않았던 저에게 실제 연구 과제를 맡김으로써 자존심을 자극해 준 것은 퍼스였습니다. 그는 저를 위해 장치를 빌려주었고, 저는 그것을 제 방으로 가져와 창가에 설치했으며, 조명 조건이 적절할 때 관찰을 수행했습니다. 그 결과는 국립 과학 아카데미 회보에 공동 명의로 출판되었습니다. 의식에서 어떤 기록도 할 수 없을 정도로 미미한 감각 효과의 흔적이 그럼에도 불구하고 판단에 영향을 미칠 수 있다는 시연은, 수년 후 제가 ''잠재 의식''에 대한 책을 집필하도록 유도한 지속적인 동기였을 수 있습니다.
이 연구는 관찰 가능한 인지 수행과 의식의 표현을 명확하게 구별한다.
스탠리 스미스 스티븐스는 멱법칙 아이디어를 부활시켰으며, 페히너의 로그-선형 함수와 대조를 이루었다(스티븐스의 멱법칙 참고). 그는 또한 자극의 강도에 대한 비율로 숫자를 할당하는 것을 옹호했으며, 이를 크기 추정이라고 불렀다. 스티븐스는 크기 생성 및 교차 양상 매칭과 같은 기술을 추가했다.
오마르 칼리파[13]는 중세 과학자 알하젠을 정신물리학의 창시자로 간주해야 한다고 주장했다. 알하 이담은 시각에 대해 많은 주관적인 보고서를 작성했지만, 그가 정량적 정신물리학 기법을 사용했다는 증거는 없으며, 그러한 주장은 반박되었다.[14]
4. 정신물리학적 함수
정신물리학적 함수는 자극과 감각의 관계를 물리학적, 수학적 방법으로 표현한 것이다.
심신과 외적 자극의 관계를 밝히는 과정에서 정신물리학적 함수가 고안되었다. 가장 기본적인 자극과 감각의 관계는 심리적인 감각량(심리량: R)이 물리적인 자극의 양(물리량: S)의 대수에 비례한다는 베버-페히너의 법칙으로 표현된다.
페히너는 물리량이 매우 작을 때는 심리량이 0이 되고, 물리량이 일정 수준을 넘어서면 심리량은 거의 증가하지 않는다고 보았다.
S. S. 스티븐스는 크기 추정법을 통해 얻은 데이터를 바탕으로 스티븐스의 멱법칙을 제시했다. 이 법칙에 따르면, 통증과 같은 위협적인 자극은 n>1, 그 외의 감각은 n<1의 값을 가진다.
이러한 함수들은 인간 감각의 보편적인 분석에는 어려움이 있어 현재 직접적인 연구는 적지만, 심리음향학, 인지심리학, 인간공학 등 다양한 분야에서 활용되고 있다. 인간의 다양한 자극을 정량적으로 측정하는 것의 어려움, 실험자의 질문에 의한 영향, 개인의 심리적, 경험적 차이 등이 문제점으로 지적되지만, 이러한 차이를 줄이기 위한 여러 실험 방법들이 고안되고 있다.
4. 1. 베버-페히너의 법칙
1860년, 구스타프 테오도어 페히너는 ''정신물리학의 원리(Elemente der Psychophysik)''를 출판하면서 정신물리학의 많은 고전적인 기법과 이론을 정립했다.[5] 그는 물리적 자극과 감각(Empfindungen)과 같은 의식의 내용 사이의 관계를 연구하기 위해 "정신물리학"이라는 용어를 만들었다. 페히너는 에른스트 하인리히 베버가 라이프치히에서 얻은 촉각과 빛에 대한 실험 결과에서 영감을 받았다.[6][7] 특히 베버는 중간 강도의 자극의 최소 식별 가능한 차이(최소 식별 차이; jnd)가 기준 강도의 일정한 비율이라는 것을 보여주었고, 페히너는 이를 베버의 법칙이라고 불렀다. 이를 통해 페히너는 오늘날 페히너 척도로 알려진 유명한 로그 척도를 도출했다.가장 기본적인 자극과 감각의 관계는 심리적인 감각량(심리량: R)은 물리적인 자극의 양(물리량: S)의 대수에 비례한다는 것이다. 이것은 "베버-페히너의 법칙" (혹은 단순히 "페히너의 법칙")으로 알려져 있다.
: ''R'' = ''k'' log₁₀ ''S'' (''k''는 감각 상수)
페히너는 물리량이 극소한 어떤 점에서 심리량은 0이 되고, 물리량이 일정 이상을 넘어도 심리량은 거의 증가하지 않는다고 했다.
4. 2. 스티븐스의 멱법칙
S. S. 스티븐스는 20세기 중엽 정신물리학을 재검토하면서, 크기 추정법으로 얻은 데이터를 바탕으로 스티븐스의 멱법칙을 유도했다. 이 법칙에 따르면 심리적 감각량(R)은 물리적 자극량(S)의 거듭제곱에 비례한다.[13]:
(K는 상수, n은 감각 종류에 따른 지수)
통증과 같이 생존에 위협이 되는 자극은 n > 1이며, 그 외의 감각은 n < 1의 값을 가진다. 스티븐스는 다양한 감각에 대한 n 값을 제시했다.
스티븐스의 멱법칙은 페히너의 로그 함수와 대조되는 개념으로, 19세기의 연구자들이 제안한 멱법칙 아이디어를 부활시킨 것이다.
하지만 이러한 함수는 인간 감각의 다양성과 측정의 어려움, 실험 질문 내용 및 개인의 경험에 따른 반응 차이 등의 문제로 인해 현재 직접적으로 연구되지는 않는다. 그럼에도 불구하고, 심리음향학, 인지심리학, 인간공학 등 다양한 분야에서 간접적으로 활용되고 있다.
5. 식역 (Threshold)
페히너는 감각의 크기를 직접적으로 측정하는 것은 불가능하지만 식역(threshold) 개념을 이용해 간접적 측정이 가능하다고 하였다. 정신물리학에서 식역(또는 한계)은 참가자가 자극의 존재(절대 식역[15]) 또는 두 자극 간의 차이(차이 역치[7])를 감지할 수 있는 강도의 지점이다. 이 역치 미만의 강도를 가진 자극은 감지할 수 없어 잠재 의식적으로 간주된다. 역치에 가까운 자극은 때때로 감지될 수 있으므로, 역치는 자극 또는 자극 변화가 특정 비율의 시행에서 감지되는 지점으로 정의된다.
정신물리학자들은 일반적으로 강도가 변하는 순수한 음이나 휘도가 변하는 빛과 같이 객관적으로 측정할 수 있는 실험 자극을 사용한다. 시각, 청각, 촉각(피부 및 장 감각 포함), 미각, 후각, 시간 감각 등 모든 정전형 감각이 연구되었다. 감각 영역에 관계없이 세 가지 주요 연구 분야는 절대 역치, 변별 역치(최소가지차), 척도이다.
5. 1. 절대 식역 (Absolute Threshold)
절대식역(absolute threshold)은 자극을 탐지할 수 있는 에너지 수준과 탐지할 수 없는 에너지 수준 사이의 경계이다. 이는 특정 자극에 대한 민감성의 한계를 나타내며, 외부 환경을 인식하는 데 중요한 역할을 한다. 고전 정신물리학에서는 특정 자극과 특정 유기체에 대해 절대식역이 존재하며, 탐지와 비탐지의 경계가 불연속적이라고 가정했다. 그러나 이후 실험을 통해 자극의 강도를 점차 높이면서 탐지 수행을 측정한 결과, 탐지 확률이 연속적으로 증가하는 것으로 밝혀졌다. 이를 바탕으로 절대식역은 탐지 확률이 50%인 자극 강도로 정의된다.[16] 예를 들어, 어둡고 맑은 밤에 약 48km 앞에서 비치는 촛불은 시각 감각 양식의 절대식역이다.정신물리학자들은 일반적으로 강도가 변하는 순수한 음이나 휘도가 변하는 빛과 같이 객관적으로 측정할 수 있는 실험 자극을 사용한다. 시각, 청각, 촉각(피부 및 장 감각 포함), 미각, 후각, 시간 감각 등 모든 감각이 연구되었다.
역치(또는 한계)는 참가자가 자극의 존재를 감지할 수 있는 강도의 지점(절대 역치[15])이다. 이 역치 미만의 강도를 가진 자극은 감지할 수 없으며 잠재 의식적으로 간주된다. 역치에 가까운 값의 자극은 경우에 따라 감지될 수 있으므로, 역치는 자극이 특정 비율의 시행에서 감지되는 지점으로 정의된다. 절대 역치는 피험자가 자극의 존재를 일정 비율(일반적으로 50%)로 감지할 수 있는 강도의 수준이다.[16] 예를 들어, 손등의 촉각에 대한 절대 역치를 생각해 보면, 참가자는 단 하나의 머리카락이 닿는 것은 느끼지 못할 수 있지만, 두세 가닥의 머리카락이 닿는 것은 감지할 수 있는데, 이는 역치를 초과하기 때문이다. 절대 역치는 종종 "탐지 역치"라고도 불린다.
5. 2. 차이 식역 (Difference Threshold)
차이 식역(difference threshold)이란 감각적으로 변별 가능한 최소한의 물리적 자극의 변화량을 의미하며, 보통 최소가지차(just noticeable difference: JND)로 나타낸다. 예를 들어 표준 자극의 무게에서 어느 정도 무게를 더 첨가하면 두 자극의 무게가 다르게 느껴지는데, 이때 표준 자극과 최소가지차의 비율은 상당히 안정된 상수 값을 가지며, 이것을 베버의 법칙이라고 한다.[17] 이는 탐지자가 자극의 절대량보다는 상대적인 차이나 변화에 더 민감하다는 것을 보여준다.차이 역치(또는 최소 가분 변별 자극, JND)는 참가자가 특정 비율의 시간 동안 감지할 수 있는, 강도가 다른 두 자극 간의 최소 차이의 크기이며, 특정 백분율은 작업에 따라 다르다.[17] 이 역치를 테스트하기 위해 여러 방법이 사용된다. 예를 들어 피험자는 다른 자극과 동일하다고 인식될 때까지 하나의 자극을 조정하도록 요청받거나(조정 방법), 두 자극 간의 차이의 방향과 크기를 설명하거나, 자극 쌍의 강도가 동일한지 다른지 결정하도록 요청받을 수 있다(강제 선택). 최소 가분 변별 자극은 고정된 양이 아니며, 자극의 강도와 테스트되는 특정 감각에 따라 달라진다.[17] 베버의 법칙에 따르면, 모든 자극에 대한 최소 가분 변별 자극은 강도의 변화와 관계없이 일정 비율이다.[18]
변별 실험에서 실험자는 두 자극(예: 두 개의 무게 또는 두 개의 소리) 간의 차이가 감지 가능한 시점을 결정하려고 한다. 피험자는 예를 들어 무게와 같은 하나의 자극을 제시받고 다른 무게가 더 무거운지 가벼운지 말하도록 요청받는다. 일부 실험에서 피험자는 두 무게가 동일하다고 표시할 수도 있는데, 주관적 등가점(PSE)에서 피험자는 두 무게를 동일하다고 인식한다. 최소 가분 변별 자극 또는 차이 한계(DL)는 피험자가 일정 비율의 시간 동안 감지하는 자극 차이의 크기이다. 일반적으로 비교 작업에서 50%가 사용된다.[19] 또한 두 대안 강제 선택(2AFC) 패러다임은 두 대안을 구별하는 데 있어 성능이 우연 수준으로 감소하는 지점을 평가하는 데 사용되며, 여기서 75%는 일반적으로 2AFC 작업에서 우연과 일치하는 50% 성공률을 나타낸다.
절대 역치와 차이 역치는 배경 잡음이 항상 자극 감지 능력을 방해하기 때문에 원칙적으로 유사한 것으로 간주되기도 한다.[6][20]
6. 감각과 지각
정신물리학은 물리적 자극과 심리적 경험 사이의 양적 관계를 체계적으로 연구하는 학문이다. 마음과 신체 사이의 관계를 연구하고자 하였는데, 예를 들어 청각의 경우 인간은 소리를 듣기 위해서는 물리적으로 생성되는 음파를 귀의 고막을 통해 청각 신경으로 전환시켜야만 한다.[31] 물질세계에 소리가 분명히 존재함에도 불구하고, 이와 상관없이 소리가 청각 신경으로 전환되어 뇌에 전달되지 않는다면 인간은 소리를 들을 수 없다.
주요 감각은 이른바 오감을 중심으로 한 지각(시각, 청각, 후각, 미각, 평형 감각, 피부 감각, 심부 감각, 내장 감각 등)으로 대표된다. 이러한 지각은 시각의 경우 눈, 미각의 경우 혀, 평형 감각은 내이 등, 몇몇 수용체에 의해 유발된다는 사실은 고대부터 알려져 있었다. 또한, 이를 해부하여 그 기구는 과학의 발전에 따라 상당 부분 해명되었다.
예를 들어 인간의 시각 기관인 안구와 비교하면 카메라는 매우 유사한 기구를 가지고 있다. 수정체는 렌즈에, 망막은 필름에 해당한다. 여기서, 우리는 망막에 맺힌 영상을 인식하고 있는데, 그 영상은 외부에서 들어온 빛에 의한 것이다. 이 빛은 물리적인 것이므로 측정이 가능하다. 이처럼 질적인 사건과 감각의 대응 관계를 물리학적인 방법으로, 이른바 인간의 지각을 블랙 박스로 간주하여 연구하는 것이 정신물리학이다.
7. 실험 방법론
정신물리학 실험은 대상자가 자극을 감지, 식별하거나, 다른 자극과 구별할 수 있는지, 또는 그 차이의 크기나 성격을 설명할 수 있는지를 확인하는 것을 목표로 한다.[6][7]
현대 감각 지각 연구에서는 지각자의 판단을 측정하여 자극에서 무엇을 추출하는지 확인한다. 매우 약한 자극의 경우에는 신호 탐지 이론이 주요 방법으로 사용된다. 스탠리 스미스 스티븐스는 구스타프 페히너의 로그-선형 함수와 대조되는 스티븐스의 멱법칙을 제안하며 19세기의 멱법칙 아이디어를 부활시켰다. 스티븐스는 크기 추정, 크기 생성, 교차 양상 매칭 등의 방법을 추가했다.
20세기 중엽, S. S. 스티븐스는 크기 추정법으로 얻은 데이터를 바탕으로 "스티븐스의 멱법칙"을 유도했다.
:
여기서 R은 감각 크기, K는 비례 상수, S는 자극 강도, n은 감각 양상에 따른 지수이다. 통증과 같은 위기적인 자극은 n>1, 그 외의 감각은 n<1의 값을 가진다. S. S. 스티븐스가 제시한 감각 종류별 감각 계수(n)는 아래 표와 같다.
7. 1. 고전적 방법
정신물리학 실험에서는 전통적으로 자극 감지 및 차이 감지 실험에서 피험자의 지각을 테스트하기 위해 세 가지 방법을 사용해 왔다.- 한계법 (Method of Limits)
한계법의 상승법은 자극을 감지할 수 없을 정도로 낮은 수준에서 시작하여 참가자가 이를 인지했다고 보고할 때까지 자극의 수준을 점진적으로 증가시키는 방식이다. 예를 들어, 최소 음향 진폭을 테스트하는 경우, 소리는 너무 조용하여 감지할 수 없게 시작하여 점차 커진다. 하강법에서는 이와 반대로 진행된다. 각 경우, 역치는 자극이 감지되는 자극 속성의 수준으로 간주된다.[22]
실험에서 상승법과 하강법을 번갈아 사용하고 역치의 평균을 구한다. 이러한 방법의 가능한 단점은 피험자가 자극을 인지한다고 보고하는 데 익숙해져 역치를 넘어서도 동일한 방식으로 계속 보고할 수 있다는 점이다(습관 오류). 반대로, 피험자는 자극이 감지 가능하거나 감지 불가능하게 될 것을 예상하고 조기에 판단을 내릴 수도 있다(예측 오류).[22]
이러한 잠재적 함정을 피하기 위해 게오르크 폰 베케시는 1960년 청각 지각 연구에서 계단식 절차를 도입했다. 이 방법에서 소리는 들리는 상태에서 시작하여 피험자의 각 반응 후에 더 조용해지며, 피험자가 소리를 듣지 못한다고 보고할 때까지 진행된다. 그 시점에서 소리는 각 단계마다 더 커지다가 피험자가 소리를 듣는다고 보고하는 시점에서 다시 단계적으로 더 조용해진다. 이러한 방식으로 실험자는 역치에 "정확히 접근"할 수 있다.[22]
- 고정 자극법 (Method of Constant Stimuli)
자극의 특정 속성의 수준이 오름차순이나 내림차순으로 제시되는 대신, 고정 자극법에서는 다음 시행과 관련이 없이 무작위로 제시된다. 이는 피험자가 다음 자극의 수준을 예측할 수 없게 하여 습관과 기대에 따른 오류를 줄여준다. '절대 역치'의 경우, 피험자는 자극을 감지할 수 있는지 여부를 다시 보고한다.[22] '차이 역치'의 경우, 각 변동 수준에 일정한 비교 자극이 있어야 한다.
프리드리히 헤겔마이어(Friedrich Hegelmaier)는 1852년 논문에서 고정 자극법을 설명했다.[23] 이 방법은 심리 측정 함수의 전체 샘플링을 허용하지만, 여러 조건이 섞여 있을 때 많은 시행이 발생할 수 있다.
- 조정법 (Method of Adjustment)
조정법에서, 피험자는 자극의 강도를 조절하고 배경 소음에 대해 감지할 수 있을 정도로 미세하게 변형하거나, 다른 자극의 강도와 같도록 변경하라는 요청을 받는다. 이 조정은 여러 번 반복된다. 이는 또한 ''평균 오차법''이라고도 한다.[22]
이 방법에서, 관찰자는 변동 자극의 크기를 스스로 조절하며, 표준 자극보다 뚜렷하게 크거나 작은 수준에서 시작하여 두 자극의 주관적인 동일성에 만족할 때까지 이를 변경한다. 각 조정 후에 변동 자극과 표준 자극 간의 차이가 기록되고, 상당한 일련의 오차가 표로 정리된다. 마지막으로 평균이 계산되어 평균 오차를 제공하며, 이는 민감도의 척도로 간주될 수 있다.
7. 2. 적응적 방법 (Adaptive Methods)
심리 측정 함수에서 수집되는 대부분의 데이터가 역치에 대한 정보를 거의 제공하지 않기 때문에, 실험의 고전적인 방법들은 종종 비효율적이라고 주장된다. 적응 계단 절차(또는 고전적인 조정 방법)를 사용하면 샘플링된 지점이 심리 측정 역치 주위에 모이도록 할 수 있다. 심리 측정 함수의 기울기에 관심이 있다면 데이터 포인트를 약간 더 넓은 범위로 분산시킬 수도 있다. 따라서 적응 방법은 역치만 추정하거나 역치 ''및'' 기울기를 모두 추정하도록 최적화할 수 있다. 적응 방법은 계단 절차와 베이지안 또는 최대 우도 방법으로 분류된다. 계단 방법은 이전 응답에만 의존하며 구현하기가 더 쉽다. 베이지안 방법은 이전의 모든 자극-반응 쌍을 고려하며 일반적으로 주의력 결핍에 대해 더 강력하다.[24] 실제 예는 여기에서 찾을 수 있다.[21]올라가고 내려가는 설계
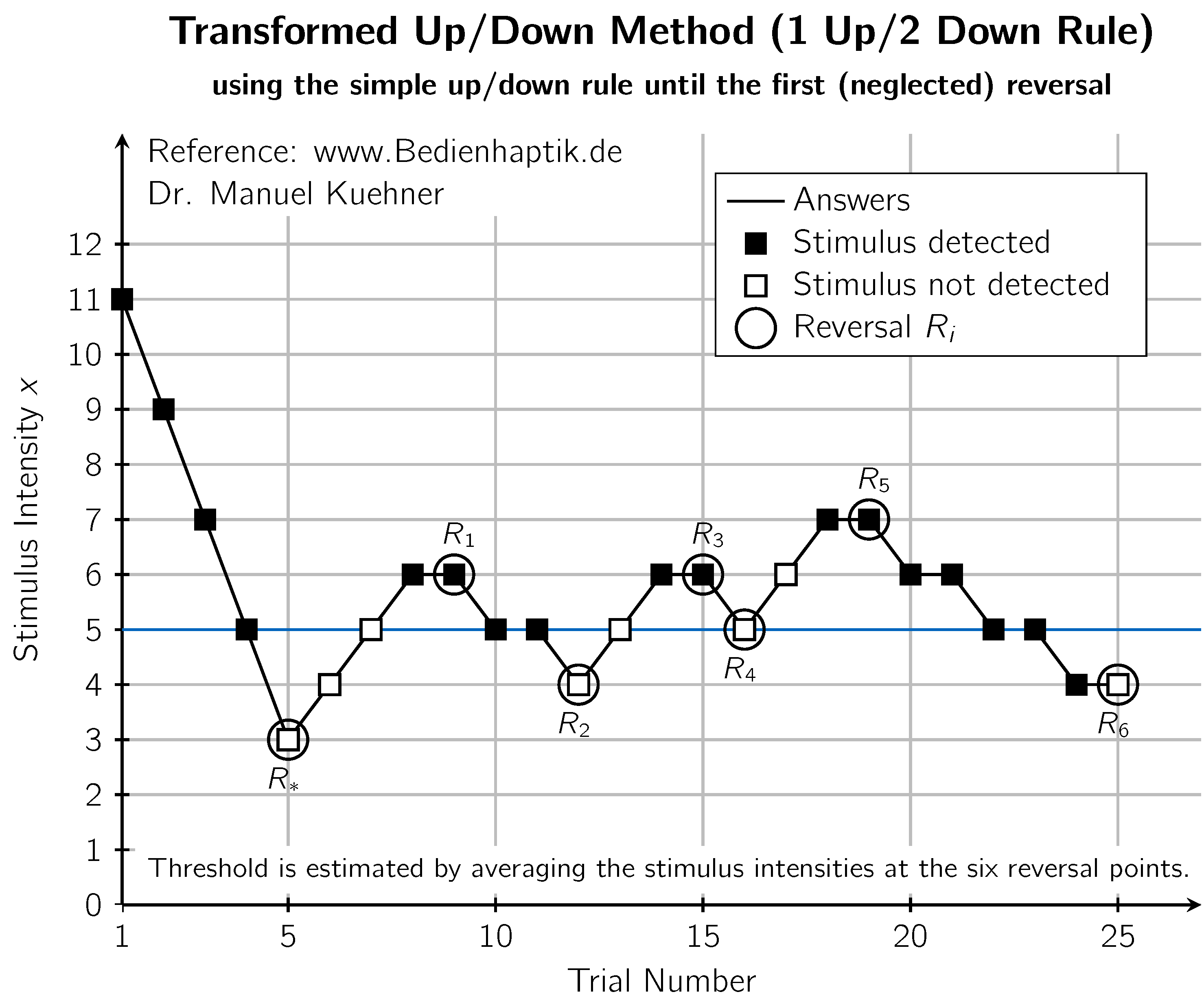
계단식 절차는 일반적으로 감지하기 쉬운 높은 강도의 자극으로 시작한다. 그런 다음 관찰자가 실수를 할 때까지 강도가 감소하고, 그러면 계단이 '반전'되고 관찰자가 올바르게 응답할 때까지 강도가 증가하여 또 다른 반전을 유발한다. 이러한 '반전'의 마지막 값은 평균화된다. 서로 다른 결정 및 종료 규칙을 사용하여 다양한 유형의 계단식 절차가 있다. 단계 크기, 상/하 규칙 및 기본 심리측정 함수의 확산은 심리측정 함수의 어느 지점에서 수렴하는지를 결정한다.[24] 계단식 절차에서 얻은 역치 값은 크게 변동될 수 있으므로 설계에 주의를 기울여야 한다. Garcia-Perez는 많은 다른 계단식 알고리즘을 모델링했으며 몇 가지 실용적인 권장 사항을 제시했다.[25]
고정된 단계 크기를 사용하는 더 일반적인 계단식 설계 중 하나는 1-상-N-하 계단이다. 참가자가 연속으로 N번 정답을 하면 자극 강도가 한 단계 크기만큼 감소한다. 참가자가 오답을 하면 자극 강도가 한 크기만큼 증가한다. 임계값은 모든 실행의 평균 중간점에서 추정된다. 이 추정치는 점근적으로 올바른 임계값에 접근한다.
7. 3. 크기 추정 (Magnitude Estimation)
전형적인 경우, 사람들은 자극의 크기에 비례하여 숫자를 할당하도록 요청받는다. 이들의 숫자 기하 평균에 대한 심리 측정 함수는 종종 안정적이고 재현 가능한 지수를 갖는 멱법칙이다.[29] 맥락이 법칙과 지수를 변경할 수 있지만, 그 변화 역시 안정적이고 재현 가능하다.[29] 숫자가 아닌 다른 감각 또는 인지 차원을 사용하여 자극과 일치시킬 수 있으며, 이 방법은 "크기 생성" 또는 "교차 양식 매칭"이 된다. 수치적 크기 추정에서 발견된 이러한 차원의 지수는 크기 생성에서 발견된 지수를 예측한다. 크기 추정은 일반적으로 리커트가 태도 척도 항목으로 사용한 것과 같은 범주형 앵커의 제한된 범위 때문에 다중 범주 응답보다 정신 물리학적 함수에 대해 더 낮은 지수를 찾는다.[29]20세기 중엽, S. S. 스티븐스 (Stanley Smith Stevens)는 크기 추정법에 의해 얻어진 데이터를 바탕으로, 아래와 같은 식으로 표현되는 "스티븐스의 멱법칙"을 유도했다.
:
통증 등 위기적인 자극은 n>1이며, 반대로 그 외의 감각 등은 n<1을 취한다고 했다. n은 아래 표와 같은 값을 취한다고 했다.
8. 정신물리학의 응용
초기의 행동경제학 및 공간 인지 과학은 심리물리학의 방법론을 많이 사용했다.
참조
[1]
서적
Psychophysics: the fundamentals
[2]
서적
Visual perception
Psychology Press
[3]
서적
Handbook of perception and human performance: Vol. I. Sensory processes and perception
John Wiley
[4]
서적
Psychophysics: the fundamentals
Lawrence Erlbaum Associates
[5]
서적
Elemente der Psychophysik (Elements of Psychophysics)
[6]
서적
Psychophysics
B Scharf
[7]
서적
Psychophysics: the fundamentals
Lawrence Erlbaum Associates
[8]
논문
On Small Differences in Sensation
http://psychclassics[...]
[9]
논문
Telepathy: Origins of Randomization in Experimental Design
1988-09
[10]
논문
A Historical View of Statistical Concepts in Psychology and Educational Research
1992-11
[11]
논문
Deception, Efficiency, and Random Groups: Psychology and the Gradual Origination of the Random Group Design
https://www.rug.nl/r[...]
1997-12
[12]
논문
Charles S. Peirce as a Teacher
https://books.google[...]
1916-12-21
[13]
논문
Who Is the Founder of Psychophysics and Experimental Psychology?
[14]
논문
Ibn al-Haytham and psychophysics
[15]
서적
Psychophysics: the fundamentals
Lawrence Erlbaum Associates
[16]
웹사이트
Experiencing Sensation and Perception
http://www.saylor.or[...]
2017-11-17
[17]
서적
Psychology
[18]
서적
Elemente der Psychophysik (Elements of Psychophysics)
[19]
서적
Psychology: the Science of Behaviour
[20]
서적
Psychophysics: the fundamentals
Lawrence Erlbaum Associates
[21]
웹사이트
Software for visual psychophysics: an overview
http://www.visionsci[...]
[22]
서적
Psychophysics: the fundamentals
Lawrence Erlbaum Associates
[23]
논문
F. Hegelmaier: On memory for the length of a line
[24]
논문
Adaptive psychophysical procedures
1995-09
[25]
논문
Forced-choice staircases with fixed step sizes: asymptotic and small-sample properties
[26]
논문
Quest: A Bayesian adaptive psychometric method
1983-03
[27]
논문
Efficient estimation of sensory thresholds
1986-11
[28]
논문
Bayesian adaptive estimation of psychometric slope and threshold
1999-08
[29]
논문
On the psychophysical law
1957
[30]
서적
本当の声を求めて 野蛮な常識を疑え
SIBAA BOOKS
[31]
서적
Psychology Press
[32]
서적
Elemente der Psychophysik (Elements of Psychophysics)
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com