조인트

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
- 2.1. 초기 역사
- 2.2. 19-20세기
3. 운동 방정식
- 3.1. 각도와 각속도 관계
- 3.2. 각가속도 관계
4. 더블 카단 조인트
- 4.1. 특징
- 4.2. 톰슨 커플링
5. 응용 분야
참조

1. 개요

조인트는 회전력을 전달하면서 각도나 위치 변화를 흡수하는 데 사용되는 기계적 연결 장치이다. 고대 짐벌 설계에서 유래되었으며, 로버트 훅에 의해 '유니버설 조인트'라는 용어가 처음 사용되었다. 카르다노 조인트, 훅 조인트 등으로도 불리며, 20세기에는 자동차, 농업 기계 등 다양한 산업 분야에서 널리 사용되었다. 조인트는 입력축과 출력축 사이의 각도 관계에 따라 속도 변화가 발생하는데, 이를 보완하기 위해 더블 카단 조인트와 같은 개선된 형태가 개발되었다. 자동차의 드라이브 샤프트, 철도 차량의 구동축 등 회전력을 전달해야 하지만 굴곡이나 변위가 있는 경우에 주로 사용된다.

더 읽어볼만한 페이지

기계공학 - 베어링
베어링은 회전 부품의 마찰을 줄여 효율성을 높이는 기계 요소로, 다양한 구조(미끄럼, 구름, 유체, 자기)와 하중, 윤활 방식에 따라 분류되며 산업 전반에 걸쳐 널리 사용되고, 수명은 사용 조건에 따라 달라진다.
기계공학 - 무인 항공기
무인 항공기는 조종사 없이 자율 또는 원격 조종으로 비행하는 동력 비행체로, 다양한 기준으로 분류되어 군사 및 민간용으로 활용되지만 안전 및 보안 위협, 사이버 공격, 악의적 사용 가능성 등의 문제점도 존재한다.
글로벌세계대백과를 인용한 문서/{{{분류 - 공 (악기)
공은 금속으로 제작된 타악기로, 다양한 문화권에서 의식, 신호, 음악 연주 등에 사용되며, 형태와 용도에 따라 여러 종류로 나뉜다.
글로벌세계대백과를 인용한 문서/{{{분류 - 국무회의
국무회의는 대한민국 대통령을 의장으로, 예산, 법률안, 외교, 군사 등 국정 현안을 심의하는 중요한 기관이며, 대통령, 국무총리, 국무위원으로 구성되고, 정례회의는 매주 1회, 임시회의는 필요에 따라 소집된다.
글로벌세계대백과를 인용한 문서/{{{분류2 - 공 (악기)
공은 금속으로 제작된 타악기로, 다양한 문화권에서 의식, 신호, 음악 연주 등에 사용되며, 형태와 용도에 따라 여러 종류로 나뉜다.
글로벌세계대백과를 인용한 문서/{{{분류2 - 국무회의
국무회의는 대한민국 대통령을 의장으로, 예산, 법률안, 외교, 군사 등 국정 현안을 심의하는 중요한 기관이며, 대통령, 국무총리, 국무위원으로 구성되고, 정례회의는 매주 1회, 임시회의는 필요에 따라 소집된다.

조인트
개요
후크 조인트
종류	자재 이음쇠
용도	동력 전달
발명가	제롤라모 카르다노
상세 정보
별칭	카르단 조인트 스파이서 조인트 후크 조인트
설명	축의 각도가 변하는 것을 허용하면서 회전 운동을 전달하는 데 사용되는 결합 또는 커플링
특징	회전 운동을 모든 각도로 전달 가능
구조	두 개의 요크, 중앙 십자형 조인트 (스파이더)
용도	자동차 구동축 조향 장치 산업 기계
장점	단순한 구조 높은 효율 단점: 속도 변화 진동
작동 원리
각도 변화 허용	두 축 사이의 각도 변화를 수용
회전 운동 전달	한 축에서 다른 축으로 회전 운동을 전달
속도 변화	각도가 커질수록 속도 변화가 커짐
응용 분야
자동차	구동축 조향 장치
산업 기계	컨베이어 벨트 펌프
항공 우주	헬리콥터 로터 항공기 엔진
참고 사항
등속 조인트	속도 변화를 보상하는 데 사용되는 특수 유형의 자재 이음쇠
이중 조인트	두 개의 자재 이음쇠를 함께 사용하여 속도 변화를 줄임

2. 역사

유니버설 조인트의 주요 개념은 고대부터 사용되어 온 짐벌 설계에 기반을 두고 있으며, 고대 그리스인들이 발리스타에 사용한 것에서 그 기원을 찾을 수 있다.^[2] 유럽에서는 16세기 이탈리아 수학자 제롤라모 카르다노의 이름을 따서 카르다노 조인트(혹은 카르단 샤프트)라고도 불린다.^[3]

1664년 가스파르 쇼트가 자신의 저서에서 이 메커니즘을 등속 조인트라고 잘못 주장하기도 했지만,^[4]^[5]^[6] 1667년에서 1675년 사이 로버트 훅이 조인트를 분석하여 회전 속도가 균일하지 않다는 것을 발견하고, 이를 활용해 해시계 면의 그림자 움직임을 추적했다.^[4] 1676년 훅은 자신의 저서 ''Helioscopes''에서 '유니버설 조인트'라는 용어를 처음 사용했으며,^[7]^[8]^[9] 1678년에 관련 설명을 발표하면서 영어권에서는 ''훅 조인트''라는 용어가 널리 쓰이게 되었다.^[10] 1683년 훅은 유니버설 조인트의 불균일한 회전 속도 문제를 해결하기 위해 중간 샤프트 양쪽 끝에서 90° 위상이 벗어난 한 쌍의 훅 조인트를 사용하는 방식을 제안했는데, 이는 현재 등속 조인트의 일종으로 알려져 있다.^[4]^[11] 이후 스웨덴의 크리스토퍼 폴헴이 유니버설 조인트를 재발명하여 스웨덴어로 ''Polhemsknut''(폴헴 매듭)이라는 이름을 얻었다.

1841년 영국의 과학자 로버트 윌리스가 유니버설 조인트의 움직임을 분석했고,^[12] 1845년에는 프랑스 엔지니어이자 수학자인 장-빅토르 퐁슬레가 구면 삼각법을 사용하여 유니버설 조인트의 움직임을 분석했다.^[13]

18세기부터 사용되기 시작한 '유니버설 조인트'라는 용어는^[10] 19세기에 들어서 널리 사용되었다. 1844년 에드먼드 모어우드의 금속 코팅 기계 특허,^[14] 1881년 에프리엄 셰이의 기관차 특허,^[15] 1884년 찰스 아미돈의 비트 브레이스 특허^[16] 등에서 유니버설 조인트가 사용되었다.

'카르단 조인트'라는 용어는 영어권에 비교적 늦게 등장했는데, 19세기의 초기 사용 사례는 대부분 프랑스어 번역이나 프랑스어의 영향을 받은 것이었다.^[18]^[19]

20세기에는 클래런스 W. 스파이서와 스파이서 제조 회사, 하디 스파이서 브랜드가 자동차 산업, 농업 기계, 중장비 등 다양한 산업 분야에서 유니버설 조인트를 대중화하는 데 크게 기여했다.

2. 1. 초기 역사

유니버설 조인트의 주요 개념은 고대부터 사용되어 온 짐벌의 설계에 기반을 두고 있다. 유니버설 조인트의 한 가지 예상 사용법은 고대 그리스인들이 발리스타에 사용한 것이다.^[2] 유럽에서 유니버설 조인트는 종종 카르다노 조인트(그리고 조인트를 사용하는 드라이브 샤프트는 카르단 샤프트)라고 불리는데, 16세기의 이탈리아 수학자 제롤라모 카르다노의 이름을 따서 명명되었다. 그는 짐벌에 대해 초기에 글을 썼지만, 그의 저술에는 유니버설 조인트가 아닌 짐벌 마운팅만 언급되어 있다.^[3]

이 메커니즘은 나중에 가스파르 쇼트의 ''Technica curiosa sive mirabilia artis''(1664)에 설명되었는데, 그는 이것이 등속 조인트라고 잘못 주장했다.^[4]^[5]^[6] 그 직후, 1667년에서 1675년 사이에 로버트 훅은 조인트를 분석했고 회전 속도가 균일하지 않다는 것을 발견했지만, 그 특성을 사용하여 해시계 면의 그림자 움직임을 추적할 수 있었다.^[4] 실제로, 시간 방정식의 성분 중 황도면에 대한 적도면의 기울기를 설명하는 것은 유니버설 조인트의 수학적 설명과 완전히 유사하다. 이 장치에 대한 '유니버설 조인트'라는 용어의 첫 번째 기록된 사용은 1676년 훅이 그의 저서 ''Helioscopes''에서 사용한 것이다.^[7]^[8]^[9] 그는 1678년에 설명을 발표했고,^[10] 그 결과 영어권에서 ''훅 조인트''라는 용어를 사용하게 되었다. 1683년, 훅은 유니버설 조인트의 불균일한 회전 속도에 대한 해결책을 제안했다. 즉, 중간 샤프트 양쪽 끝에서 90° 위상이 벗어난 한 쌍의 훅 조인트는 현재 일종의 등속 조인트로 알려진 배열이다.^[4]^[11] 스웨덴의 크리스토퍼 폴헴은 나중에 유니버설 조인트를 재발명하여 스웨덴어로 ''Polhemsknut''(폴헴 매듭)이라는 이름을 얻었다.

1841년, 영국의 과학자 로버트 윌리스는 유니버설 조인트의 움직임을 분석했다.^[12] 1845년까지 프랑스 엔지니어이자 수학자인 장-빅토르 퐁슬레는 구면 삼각법을 사용하여 유니버설 조인트의 움직임을 분석했다.^[13]

'유니버설 조인트'라는 용어는 18세기에 사용되었으며^[10] 19세기에 널리 사용되었다. 에드먼드 모어우드의 1844년 금속 코팅 기계 특허는 엔진과 압연기 샤프트 사이의 작은 정렬 오류를 수용하기 위해 해당 이름으로 유니버설 조인트를 요구했다.^[14] 예를 들어, 에프리엄 셰이의 기관차 1881년 특허는 기관차의 드라이브 샤프트에 이중 유니버설 조인트를 사용했다.^[15] 찰스 아미돈은 1884년 특허받은 그의 비트 브레이스에 훨씬 더 작은 유니버설 조인트를 사용했다.^[16] 보챔 타워의 구형, 회전식, 고속 증기 엔진은 유니버설 조인트의 개조품을 사용했다.^[17]

'카르단 조인트'라는 용어는 영어에 늦게 등장한 것으로 보인다. 19세기에 사용된 많은 초기 사례는 프랑스어 번역에서 나타나거나 프랑스어 사용의 영향을 많이 받았다. 예로는 1867년 ''파리 만국 박람회''에 대한 보고서^[18]와 1881년에 프랑스어에서 번역된 다이나모미터에 대한 기사가 있다.^[19]

2. 2. 19-20세기

유니버설 조인트의 주요 개념은 고대부터 사용되어 온 짐벌의 설계에 기반을 두고 있다. 유니버설 조인트의 한 가지 예상 사용법은 고대 그리스인들이 발리스타에 사용한 것이다.^[2] 유럽에서 유니버설 조인트는 종종 카르다노 조인트(그리고 조인트를 사용하는 드라이브 샤프트는 카르단 샤프트)라고 불리는데, 16세기의 이탈리아 수학자 제롤라모 카르다노의 이름을 따서 명명되었다. 그는 짐벌에 대해 초기에 글을 썼지만, 그의 저술에는 유니버설 조인트가 아닌 짐벌 마운팅만 언급되어 있다.^[3]

이 메커니즘은 나중에 가스파르 쇼트의 ''Technica curiosa sive mirabilia artis''(1664)에 설명되었는데, 그는 이것이 등속 조인트라고 잘못 주장했다.^[4]^[5]^[6] 그 직후, 1667년에서 1675년 사이에 로버트 훅은 조인트를 분석했고 회전 속도가 균일하지 않다는 것을 발견했지만, 그 특성을 사용하여 해시계 면의 그림자 움직임을 추적할 수 있었다.^[4] 실제로, 시간 방정식의 성분 중 황도면에 대한 적도면의 기울기를 설명하는 것은 유니버설 조인트의 수학적 설명과 완전히 유사하다. 이 장치에 대한 '유니버설 조인트'라는 용어의 첫 번째 기록된 사용은 1676년 훅이 그의 저서 ''Helioscopes''에서 사용한 것이다.^[7]^[8]^[9] 그는 1678년에 설명을 발표했고,^[10] 그 결과 영어권에서 ''훅 조인트''라는 용어를 사용하게 되었다. 1683년, 훅은 유니버설 조인트의 불균일한 회전 속도에 대한 해결책을 제안했다. 즉, 중간 샤프트 양쪽 끝에서 90° 위상이 벗어난 한 쌍의 훅 조인트는 현재 일종의 등속 조인트로 알려진 배열이다.^[4]^[11] 스웨덴의 크리스토퍼 폴헴은 나중에 유니버설 조인트를 재발명하여 스웨덴어로 ''Polhemsknut''(폴헴 매듭)이라는 이름을 얻었다.

1841년, 영국의 과학자 로버트 윌리스는 유니버설 조인트의 움직임을 분석했다.^[12] 1845년까지 프랑스 엔지니어이자 수학자인 장-빅토르 퐁슬레는 구면 삼각법을 사용하여 유니버설 조인트의 움직임을 분석했다.^[13]

'유니버설 조인트'라는 용어는 18세기에 사용되었으며^[10] 19세기에 널리 사용되었다. 에드먼드 모어우드의 1844년 금속 코팅 기계 특허는 엔진과 압연기 샤프트 사이의 작은 정렬 오류를 수용하기 위해 해당 이름으로 유니버설 조인트를 요구했다.^[14] 예를 들어, 에프리엄 셰이의 기관차 1881년 특허는 기관차의 드라이브 샤프트에 이중 유니버설 조인트를 사용했다.^[15] 찰스 아미돈은 1884년 특허받은 그의 비트 브레이스에 훨씬 더 작은 유니버설 조인트를 사용했다.^[16] 보챔 타워의 구형, 회전식, 고속 증기 엔진은 유니버설 조인트의 개조품을 사용했다.^[17]

'카르단 조인트'라는 용어는 영어에 늦게 등장한 것으로 보인다. 19세기에 사용된 많은 초기 사례는 프랑스어 번역에서 나타나거나 프랑스어 사용의 영향을 많이 받았다. 예로는 1867년 ''파리 만국 박람회''에 대한 보고서^[18]와 1881년에 프랑스어에서 번역된 다이나모미터에 대한 기사가 있다.^[19]

20세기에는 클래런스 W. 스파이서와 스파이서 제조 회사, 그리고 하디 스파이서 후속 브랜드가 자동차 산업, 농업 기계, 중장비, 산업 기계 개요 산업에서 유니버설 조인트를 더욱 대중화하는 데 기여했다.

3. 운동 방정식

카르단 조인트는 입력축이 일정한 속도로 회전해도 출력축은 가변 속도로 회전하여 진동과 마모를 유발하는 주요 문제점을 가지고 있다. 이러한 출력축의 속도 변화는 조인트의 구성, 즉 입력축의 회전 각도( $\gamma_1$ ), 출력축의 회전 각도( $\gamma_2$ ), 그리고 두 축이 이루는 각도( $\beta$ )에 따라 달라진다.

위 그래프에서 볼 수 있듯이, 각속도는 선형적인 관계가 아니라 회전축의 절반 주기로 주기적인 변화를 보인다.

3. 1. 각도와 각속도 관계

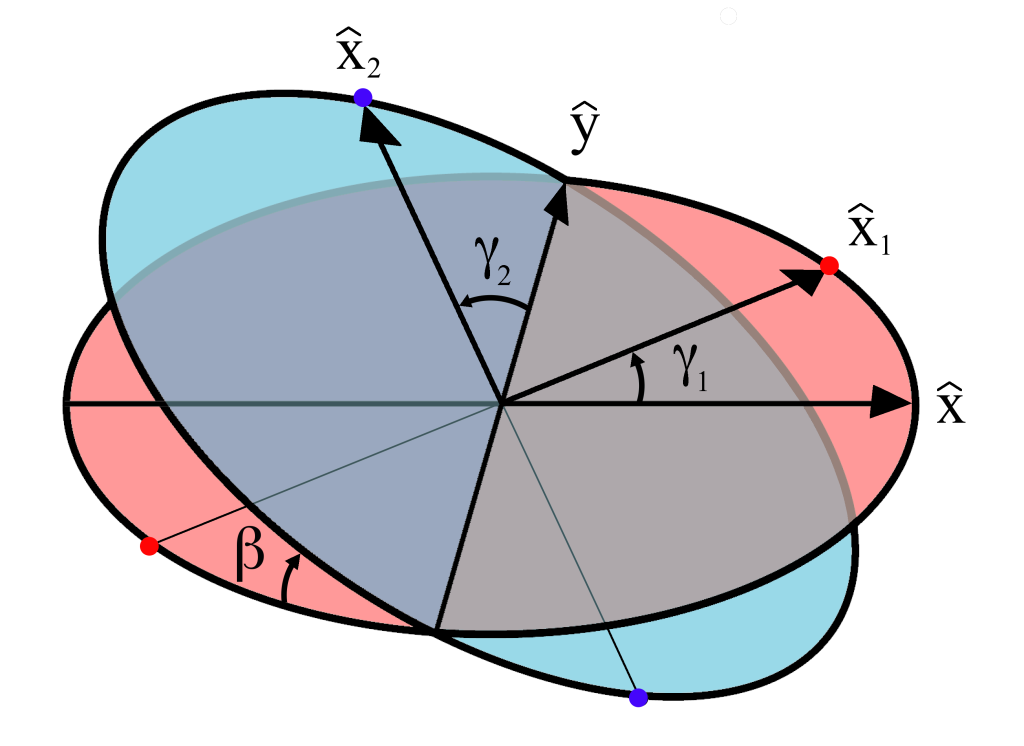
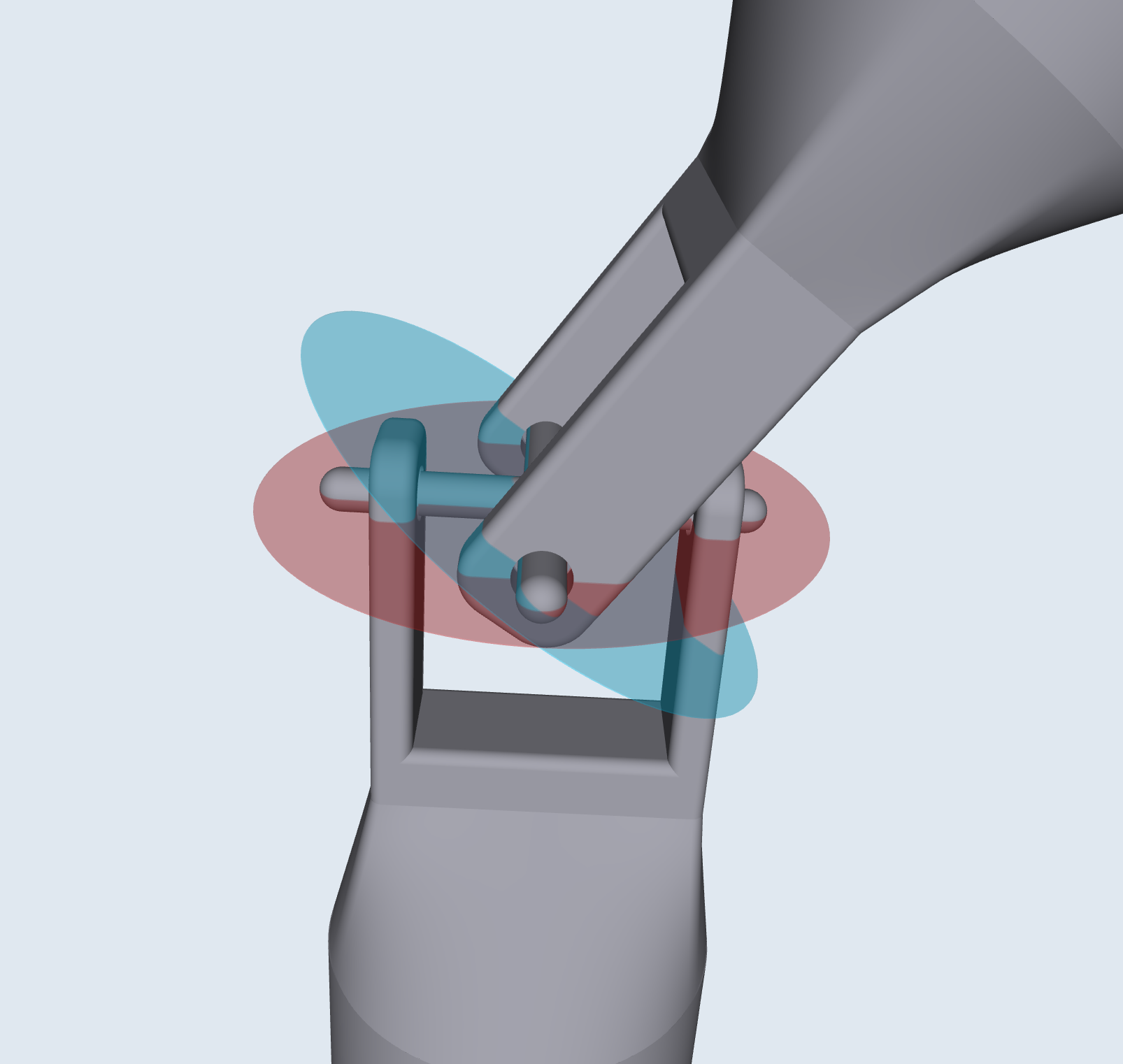
유니버설 조인트의 변수 다이어그램. 축 1은 항상 빨간색 평면에 수직이고 축 2는 항상 파란색 평면에 수직이다. 이 평면들은 서로에 대해 각도 β를 이룬다. 각 축의 각변위(회전 위치)는 각각 γ₁과 γ₂로 주어지며, 이는 x 및 y축을 따라 초기 위치에 대한 단위 벡터 x̂₁과 x̂₂의 각도이다. x̂₁과 x̂₂ 벡터는 두 축을 연결하는 짐벌에 의해 고정되므로 항상 서로 수직으로 유지되도록 제한된다.

운동 방정식에 대한 다이어그램에 색상으로 표시된 샘플 유니버설 조인트. 빨간색과 파란색 평면이 보인다.

카르단 조인트는 입력 구동축이 일정한 속도로 회전하더라도 출력 구동축은 가변 속도로 회전하여 진동과 마모를 유발하는 주요 문제점을 가지고 있다. 구동축의 속도 변화는 조인트의 구성에 따라 달라지며, 이는 다음 세 가지 변수로 지정된다.

$\gamma_1$ : 축 1의 회전 각도
$\gamma_2$ : 축 2의 회전 각도
$\beta$ : 조인트의 굽힘 각도 (축이 서로 이루는 각도, 0은 평행)

이 변수들은 오른쪽 다이어그램에 나와 있다. 또한 단위 벡터

\hat{\mathbf{x}}

와

\hat{\mathbf{y}}

가 있는 고정된 좌표축과 각 축의 회전면도 표시된다. 이러한 회전면은 회전축에 수직이며 축이 회전함에 따라 움직이지 않는다. 두 축은 짐벌에 의해 연결된다. 축 1은 다이어그램의 빨간색 회전면의 빨간색 점에 짐벌에 연결되고, 축 2는 파란색 평면의 파란색 점에 연결된다. 회전하는 축에 대해 고정된 좌표계는 x축 단위 벡터(

\hat{\mathbf{x}}_1

및

\hat{\mathbf{x}}_2

)가 원점에서 연결점 중 하나를 향하도록 정의된다.

\hat{\mathbf{x}}_1

은 ''x''축을 따라 시작 위치에서 각도

\gamma_1

에 있고,

\hat{\mathbf{x}}_2

는 ''y''축을 따라 시작 위치에서 각도

\gamma_2

에 있다.

\hat{\mathbf{x}}_1

은 다이어그램의 "빨간색 평면"에 제한되어 있으며

\gamma_1

과 관련이 있다.

:

\hat{\mathbf{x}}_1 = \left[\cos\gamma_1\,,\, \sin\gamma_1\,,\,0\right]

\hat{\mathbf{x}}_2

는 다이어그램의 "파란색 평면"에 제한되어 있으며 ''x''축의 단위 벡터

\hat{x} = [1, 0, 0]

이 오일러 각

\left[\tfrac{\pi}{2}\,,\, \beta\,,\, \gamma_2\right]

를 통해 회전한 결과이다.

:

\hat{\mathbf{x}}_2 = \left[-\cos\beta\sin\gamma_2\,,\, \cos\gamma_2\,,\, \sin\beta\sin\gamma_2\right]

\hat{\mathbf{x}}_1

및

\hat{\mathbf{x}}_2

벡터는 짐벌에 고정되어 있으므로 서로 직교해야 한다. 이는 그들의 점곱이 0일 때 만족된다.

:

\hat{\mathbf{x}}_1 \cdot \hat{\mathbf{x}}_2 = 0

따라서 두 각도 위치를 관련시키는 운동 방정식은 다음과 같다.

:

\tan\gamma_1 = \cos\beta\tan\gamma_2\,

\gamma_2

에 대한 공식적인 해는 다음과 같다.

:

\gamma_2 = \arctan\left[\tan\gamma_1 \sec\beta\right]\,

아크탄젠트 함수가 다중 값 함수이므로

\gamma_2

에 대한 해는 유일하지 않지만, 관심 각도에서 연속적이어야 한다. 예를 들어, atan2(''y'',''x'') 함수를 사용하는 다음 명시적 해는

-\pi < \gamma_1 < \pi

에 유효하다.

:

\gamma_2 = \operatorname{atan2}\left(\sin\gamma_1, \cos\beta\, \cos\gamma_1\right)

회전 조인트의 각도

\gamma_1

과

\gamma_2

는 시간의 함수이다. 운동 방정식을 시간에 대해 미분하고 변수를 제거하기 위해 운동 방정식 자체를 사용하면 각속도

\omega_1 = \frac{d\gamma_1}{dt}

와

\omega_2 = \frac{d\gamma_2}{dt}

의 관계가 생성된다.

:

\omega_2 = \omega_1\left(\frac{\cos\beta}{1 - \sin^2\beta\,\cos^2\gamma_1}\right)

각속도는 선형적으로 관련되지 않고 회전축의 절반 주기와 함께 주기적이다. 각속도 방정식은 다시 미분하여 각가속도

a_1

과

a_2

의 관계를 구할 수 있다.

:

a_2 = \frac{a_1\cos\beta}{1 - \sin^2\beta\,\cos^2\gamma_1} - \frac{\omega_1^2\cos\beta\,\sin^2\beta\,\sin 2\gamma_1}{\left(1 - \sin^2\beta\,\cos^2\gamma_1\right)^2}

입력축과 출력축의 교차각을

\varphi

, 입력축의 회전각을

\theta

라고 하면, 입출력 각속도비

\frac{\omega_2}{\omega_1}

는 다음과 같이 나타낼 수 있다.

:

\frac{\omega_2}{\omega_1} = \frac{\cos\varphi}{1-\sin^2\theta \sin^2\varphi}

이 식으로부터 교차각에 따라 출력축은 속도 변동을 일으킨다는 것을 알 수 있다.

두 개의 카르단 조인트를 일렬로 연결하면, 양쪽 조인트의 편위 각도가 같은 경우에 한하여 속도 변동을 보정할 수 있다.^[23]

3. 2. 각가속도 관계

카르단 조인트는 입력 구동축이 일정한 속도로 회전하더라도 출력 구동축은 가변 속도로 회전하여 진동과 마모를 유발하는 주요 문제점이 있다. 구동축의 속도 변화는 조인트의 구성에 따라 달라지며, 다음의 세 가지 변수로 지정된다.

$\gamma_1$ : 축 1의 회전 각도
$\gamma_2$ : 축 2의 회전 각도
$\beta$ : 조인트의 굽힘 각도 또는 축이 서로 이루는 각도로, 0은 평행 또는 직선이다.

두 축을 연결하는 짐벌에 의해

\hat{\mathbf{x}}_1

과

\hat{\mathbf{x}}_2

벡터는 서로 수직을 유지해야 한다. 이는 그들의 점곱이 0일 때를 만족해야 한다.

\hat{\mathbf{x}}_1 \cdot \hat{\mathbf{x}}_2 = 0

따라서 두 각도 위치를 관련시키는 운동 방정식은 다음과 같다.

\tan\gamma_1 = \cos\beta\tan\gamma_2\,

회전 조인트의 각도

\gamma_1

과

\gamma_2

는 시간의 함수가 된다. 운동 방정식을 시간에 대해 미분하고 변수를 제거하기 위해 운동 방정식 자체를 사용하면 각속도

\omega_1 = \frac{d\gamma_1}{dt}

와

\omega_2 = \frac{d\gamma_2}{dt}

의 관계가 생성된다.

\omega_2 = \omega_1\left(\frac{\cos\beta}{1 - \sin^2\beta\,\cos^2\gamma_1}\right)

각속도 방정식은 다시 미분하여 각가속도

a_1

과

a_2

의 관계를 구할 수 있다.

a_2 = \frac{a_1\cos\beta}{1 - \sin^2\beta\,\cos^2\gamma_1} - \frac{\omega_1^2\cos\beta\,\sin^2\beta\,\sin 2\gamma_1}{\left(1 - \sin^2\beta\,\cos^2\gamma_1\right)^2}

4. 더블 카단 조인트

더블 카단 조인트는 중심 요크를 사이에 두고 서로 마주보게 장착된 두 개의 유니버셜 조인트로 구성되며, 중심 요크는 중간 샤프트를 대체한다. 입력 샤프트와 중심 요크 사이의 각도가 중심 요크와 출력 샤프트 사이의 각도와 같으면, 두 번째 카단 조인트는 첫 번째 카단 조인트에 의해 발생하는 속도 오차를 상쇄한다. 이렇게 정렬된 더블 카단 조인트는 CV 조인트와 같은 역할을 한다.^[20]

수학적으로 표현하면 다음과 같다. 구동 샤프트와 중간 샤프트를 연결하는 유니버셜 조인트의 입력 및 출력 각도를 각각 $\gamma_1$, $\gamma_2$라 하고, 중간 샤프트와 출력 샤프트를 연결하는 유니버셜 조인트의 입력 및 출력 각도를 각각 $\gamma_3$, $\gamma_4$라 하자. 각 쌍이 서로 $\beta$ 각도를 이룬다면, 다음 관계가 성립한다.

$\tan\gamma_2 = \cos\beta\,\tan\gamma_1\qquad \tan\gamma_4 = \cos\beta\,\tan\gamma_3$

두 번째 유니버셜 조인트가 첫 번째 조인트에 대해 90도 회전하면 $\gamma_3 = \gamma_2 + \tfrac{\pi}{2}$가 된다. $\tan\left(\gamma + \tfrac{\pi}{2}\right) = \frac{1}{\tan\gamma}$라는 사실을 이용하면, 다음을 얻는다.

$\tan\gamma_4 = \frac{\cos\beta}{\tan\gamma_2} = \frac{1}{\tan\gamma_1} = \tan\left(\gamma_1 + \tfrac{\pi}{2}\right)\,$

결과적으로 출력 구동은 입력 샤프트와 90도 위상차를 가지며, 일정한 속도 구동을 얻게 된다.

유니버셜 조인트의 입력 및 출력 샤프트 각도를 측정하는 기준은 서로 수직인 축이다. 따라서 중간 샤프트의 포크는 서로 평행하다. 이는 한 포크는 입력으로, 다른 포크는 출력으로 작용하며, 앞서 언급한 90도의 위상차가 포크 간에 적용되기 때문이다.

4. 1. 특징

더블 카단 조인트 드라이브 샤프트라고 알려진 구성은 불규칙한 회전 문제를 부분적으로 해결한다. 이 구성은 중간 샤프트로 연결된 두 개의 U-조인트를 사용하며, 두 번째 U-조인트는 첫 번째 U-조인트와 관련하여 위상이 조정되어 각속도 변화를 상쇄한다. 이 구성에서 구동 샤프트와 피동 샤프트가 중간 샤프트에 대해 동일한 각도를 이루고 (하지만 반드시 같은 평면에 있을 필요는 없음) 두 개의 유니버셜 조인트가 90도 위상차를 갖는다면 피동 샤프트의 각속도는 구동 샤프트의 각속도와 일치한다. 이 조립체는 일반적으로 후륜구동 차량에 사용되며, 여기서 드라이브 샤프트 또는 프로펠러 샤프트라고 한다.^[20]

구동 샤프트와 피동 샤프트가 중간 샤프트에 대해 동일한 각도를 이루더라도 이러한 각도가 0보다 크면 회전하면서 세 개의 샤프트에 진동 모멘트가 가해진다. 이러한 모멘트는 샤프트의 공통 평면에 수직인 방향으로 샤프트를 구부리는 경향이 있다. 이는 지지 베어링에 힘을 가하며 후륜구동 차량에서 "출발 떨림"을 유발할 수 있다.^[20] 중간 샤프트는 또한 정현파 구성 요소를 각속도에 갖게 되며, 이는 진동과 응력에 기여한다.

더블 카단 조인트는 중심 요크를 사이에 두고 서로 마주보게 장착된 두 개의 유니버셜 조인트로 구성되며, 중심 요크는 중간 샤프트를 대체한다. 입력 샤프트와 중심 요크 사이의 각도가 중심 요크와 출력 샤프트 사이의 각도와 같으면 두 번째 카단 조인트는 첫 번째 카단 조인트에 의해 발생하는 속도 오차를 상쇄하며, 정렬된 더블 카단 조인트는 CV 조인트 역할을 한다.

4. 2. 톰슨 커플링

톰슨 커플링은 이중 카단 조인트를 개선한 것이다. 복잡성이 크게 증가하지만, 효율성은 약간 향상된다.

5. 응용 분야

자유이음은 자동차의 프로펠러 샤프트와 드라이브 샤프트 뿐만 아니라 철도 차량의 구동축이나 프로펠러 샤프트에도 사용되는 등, 회전력을 전달해야 하지만 굴곡이나 변위가 있어 하나의 축으로 만들 수 없는 경우, 그 각도나 위치의 변동을 흡수하기 위해 사용된다.

5. 1. 자동차

자유이음은 자동차의 프로펠러 샤프트와 드라이브 샤프트뿐만 아니라 철도 차량의 구동축이나 프로펠러 샤프트에도 사용된다. 회전력을 전달해야 하지만 굴곡이나 변위가 있어 하나의 축으로 만들 수 없는 경우, 그 각도나 위치 변동을 흡수하기 위해 사용된다.

5. 2. 철도 차량

자유이음은 자동차의 프로펠러 샤프트와 드라이브 샤프트 뿐만 아니라 철도 차량의 구동축이나 프로펠러 샤프트에도 사용된다. 회전력을 전달해야 하지만 굴곡이나 변위가 있어 하나의 축으로 만들 수 없는 경우, 그 각도나 위치의 변동을 흡수하기 위해 사용된다.

5. 3. 산업 기계

자유이음은 자동차의 프로펠러 샤프트와 드라이브 샤프트뿐만 아니라 철도 차량의 구동축이나 프로펠러 샤프트에도 사용된다. 회전력을 전달해야 하지만 굴곡이나 변위가 있어 하나의 축으로 만들 수 없는 경우, 그 각도나 위치의 변동을 흡수하기 위해 사용된다.

5. 4. 기타

자유이음은 자동차의 프로펠러 샤프트와 드라이브 샤프트 뿐만 아니라 철도 차량의 구동축이나 프로펠러 샤프트에도 사용되는 등, 회전력을 전달해야 하지만 굴곡이나 변위가 있어 하나의 축으로 만들 수 없는 경우, 그 각도나 위치의 변동을 흡수하기 위해 사용된다.

참조

_[1] 웹사이트 Kinematics with MicroStation - Ch02 J Hookes Joint https://www.youtube.[...] 2018-05-04
_[2] 웹인용 Universal Joint,Universal Joint inventors http://www.edubilla.[...] 2017-04-21
_[3] 간행물 "Cardano v. Tartaglia: The Great Feud Goes Supernatural" https://arxiv.org/ft[...] Arxiv.org 2013
_[4] 간행물 Principles of Mechanism http://rsnr.royalsoc[...] Notes & Records of the Royal Society 2007
_[5] 서적 Technica Curiosa, sive Mirabilia Artis, Libris XII. … https://books.google[...] Johannes Andreas Endter & Wolfgang Endter 1664
_[6] 서적 Principles of Mechanism https://books.google[...] Longmans, Green, and Co. 1870
_[7] 문서 "universal, ''a. (adv.)'' and ''n.''" Oxford English Dictionary Online 2010-06-16
_[8] 서적 Animadversions on the first part of the Machina Coelestis https://books.google[...] John Martyn 1674
_[9] 서적 A Description of Helioscopes, and Some Other Instruments https://books.google[...] John Martyn 1676
_[10] 간행물 Review of Ferdinand Berthoud's Treatise on Marine Clocks, Appendix Art. VIII https://books.google[...] The Monthly Review or Literary Journal 1774
_[11] 서적 Early Science in Oxford Dawsons of Pall Mall 1930
_[12] 서적 Principles of Mechanisms https://books.google[...] John W. Parker 1841
_[13] 서적 Traité de mécanique appliquée aux machines https://books.google[...] Librairie scientifique et industrielle 1845
_[14] 논문 Improvement in Coating Iron and Copper https://patents.goog[...] U.S. Patent 3,746 1844-09-17
_[15] 논문 Locomotive-Engine https://patents.goog[...] U.S. Patent 242,992 1881-06-14
_[16] 논문 Bit-Brace https://patents.goog[...] U.S. Patent 298,542 1884-05-13
_[17] 웹사이트 The Tower Spherical Engine http://www.douglas-s[...]
_[18] 간행물 Report of the Commissioner to the Paris Exposition, 1867, Chapter 1 https://books.google[...] Gelwicks, Sacramento 1868
_[19] 간행물 The Dynamometer Balance Van Nostrand's Engineering Magazine 1881-12
_[20] 웹사이트 Electronically-controlled adjustable height bearing support bracket - US Patent 6345680 http://www.patentsto[...]
_[21] 간행물 B 1454 JIS
_[22] 웹사이트 自動車用等速ジョイントの変遷と最近の技術 http://www.ntn.co.jp[...] NTN TECHNICAL REVIEW No.70 2018-01-30
_[23] 웹사이트 ユニバーサルジョイントの一般説明および選択 http://www.taiyo-kok[...] 太陽工機株式会社 2016-09-10

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com