층류

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 층류와 난류의 구분
- 2.1. 레이놀즈 수
- 2.2. 유동 형태
3. 관수로의 층류 흐름
4. 층류의 응용
참조

1. 개요

층류는 유체의 흐름 형태 중 하나로, 유체가 층을 이루며 규칙적으로 흐르는 현상을 의미한다. 층류는 레이놀즈 수에 의해 결정되며, 레이놀즈 수가 낮을수록 층류가 발생하기 쉽다. 층류는 관수로, 날개 위 공기 흐름, 얕은 물의 흐름 등 다양한 곳에서 관찰되며, 층류 후드, 에어 커튼, 층류 반응기 등 다양한 분야에 응용된다.

더 읽어볼만한 페이지

유체역학 - 양력
양력은 유체 속에서 물체가 받는 수직 방향의 힘이며, 받음각, 익형, 공기 밀도 등에 따라 달라지며 항공기 날개, 헬리콥터, 선박 프로펠러 등에서 활용된다.
유체역학 - 무인 항공기
무인 항공기는 조종사 없이 자율 또는 원격 조종으로 비행하는 동력 비행체로, 다양한 기준으로 분류되어 군사 및 민간용으로 활용되지만 안전 및 보안 위협, 사이버 공격, 악의적 사용 가능성 등의 문제점도 존재한다.

층류

2. 층류와 난류의 구분

층류와 난류를 구분하는 중요한 요소는 레이놀즈 수라는 무차원 수이다. 레이놀즈 수는 유체의 관성력과 전단 응력의 비율을 나타내며, 유체가 얼마나 빨리 움직이고 얼마나 점성이 있는지에 따라 달라진다.

일반적으로 유체가 느리게 움직이거나 점성이 매우 높을 때 층류가 발생한다. 레이놀즈 수가 증가하면, 흐름은 층류에서 난류로 전환되는데, 이 전환 범위는 유체의 작은 교란이나 흐름 시스템의 불완전성에 따라 달라진다.^[3]

관 내 흐름의 경우, 유선이 관 축과 평행하며, 관 벽에 가까울수록 유속이 작아지고 중심에서 최대가 된다. 이는 유체가 관 벽으로부터 마찰 항력을 받기 때문이다. 원관로의 층류는 하겐-포아즈유 흐름(Hagen-Poiseuille flow)이라고 불린다. 반면, 난류는 크고 작은 와류가 발생하는 격렬한 흐름이다.

관의 지름이 작고, 유속이 작고, 밀도가 작고, 점성이 클수록 층류가 되기 쉽고, 그 반대일수록 난류가 되기 쉽다.

2. 1. 레이놀즈 수

어떤 유동이 층류인지 난류인지를 기술하는 데에 중요한 인자가 되는 것이 무차원 수(dimensionless number)인 '''레이놀즈 수'''이다.

관수로 흐름의 경우 레이놀즈 수가 2100 이하이면 층류, 2900에서 4000 사이이면 천이 영역, 4000 이상이면 난류라고 한다. 명확한 구분은 없어서 어떤 경우는 2000에서 4000 사이를 천이 영역으로 보기도 한다.^[1] 개수로의 경우

Re = \frac{VD}{\nu} =500

이하이면 층류라고 한다. 이때 D는 관 직경이 아니라 개수로이므로 동수반경 R을 사용한다.^[2]

레이놀즈 수가 1보다 훨씬 작은 경우는 스토크스 유동(Stokes flow)이 된다. 이는 층류의 극단적인 경우로서, 유동에서 관성에 의한 힘보다 점성에 의한 힘의 효과가 훨씬 큰 경우이다.^[3]

채널 내 유체에서 발생하는 흐름의 유형은 유체 역학 문제에서 중요하며, 결과적으로 유체 시스템의 열전달 및 물질 전달에 영향을 미친다. 무차원수인 레이놀즈 수는 완전 발달된 흐름 조건이 층류 또는 난류 흐름으로 이어지는지 설명하는 방정식에서 중요한 매개변수이다. 레이놀즈 수는 관성력과 유체의 전단 응력의 비율이다. 즉, 유체 시스템의 규모와 관계없이 유체가 얼마나 빨리 움직이는지, 유체가 얼마나 점성인지에 대한 것이다. 층류는 일반적으로 유체가 느리게 움직이거나 유체가 매우 점성이 있을 때 발생한다. 레이놀즈 수가 증가하면, 예를 들어 유체의 유량을 증가시킴으로써, 흐름은 특정 범위의 레이놀즈 수에서 층류에서 난류 흐름으로 전환되는데, 이 층류-난류 천이 범위는 유체의 작은 교란 수준 또는 흐름 시스템의 불완전성에 따라 달라진다. 레이놀즈 수가 1보다 훨씬 작은 경우, 유체는 유체의 점성력이 관성력을 지배하는 스토크스 흐름 또는 크리핑 흐름을 나타낸다.

레이놀즈 수의 특정 계산과 층류가 발생하는 값은 흐름 시스템 및 흐름 패턴의 기하학적 구조에 따라 달라진다. 일반적인 예는 흐름 조절을 통해 파이프를 통한 흐름이며, 여기서 레이놀즈 수는 다음과 같이 정의된다.

:

\mathrm{Re} = \frac{\rho u D_\text{H}}{\mu} = \frac{u D_\text{H}}{\nu} = \frac{Q D_\text{H}}{\nu A},

여기서:

는 파이프의 수력 지름 (m)이다.
는 체적 유량 (m³/s)이다.
는 파이프의 단면적 (m²)이다.
는 유체의 평균 속도 (SI 단위: m/s)이다.
는 유체의 동점성 계수 (Pa·s = N·s/m² = kg/(m·s))이다.
는 유체의 동점성 계수, (m²/s)이다.
는 유체의 밀도 (kg/m³)이다.

이러한 시스템의 경우, 레이놀즈 수가 약 2,040 미만의 임계값 미만일 때 층류가 발생하지만, 전형적으로 1,800에서 2,100 사이의 전환 범위를 갖는다.^[4]

유체 내에 매달린 물체 주변의 흐름과 같이 외부 표면에서 발생하는 유체 시스템의 경우, 물체 주변의 흐름 유형을 예측하기 위해 레이놀즈 수에 대한 다른 정의를 사용할 수 있다. 예를 들어, 유동 유체에 매달린 입자의 경우 입자 레이놀즈 수 Re_p가 사용된다. 파이프 내 흐름과 마찬가지로, 층류는 일반적으로 낮은 레이놀즈 수에서 발생하고, 와류 발생과 같은 난류 흐름 및 관련 현상은 더 높은 레이놀즈 수에서 발생한다.

2. 2. 유동 형태

채널 내 유체에서 발생하는 흐름의 유형은 유체 역학 문제에서 중요하며, 결과적으로 유체 시스템의 열전달 및 물질 전달에 영향을 미친다. 무차원수인 레이놀즈 수는 완전 발달된 흐름 조건이 층류 또는 난류 흐름으로 이어지는지 설명하는 방정식에서 중요한 매개변수이다. 레이놀즈 수는 관성력과 유체의 전단 응력의 비율이다. 즉, 유체 시스템의 규모와 관계없이 유체가 얼마나 빨리 움직이는지, 유체가 얼마나 점성인지에 대한 것이다. 층류는 일반적으로 유체가 느리게 움직이거나 유체가 매우 점성이 있을 때 발생한다. 레이놀즈 수가 증가하면, 예를 들어 유체의 유량을 증가시킴으로써, 흐름은 특정 범위의 레이놀즈 수에서 층류에서 난류 흐름으로 전환되는데, 이 층류-난류 천이 범위는 유체의 작은 교란 수준 또는 흐름 시스템의 불완전성에 따라 달라진다. 레이놀즈 수가 1보다 훨씬 작은 경우, 유체는 유체의 점성력이 관성력을 지배하는 스토크스 흐름 또는 크리핑 흐름을 나타낸다.

레이놀즈 수의 특정 계산과 층류가 발생하는 값은 흐름 시스템 및 흐름 패턴의 기하학적 구조에 따라 달라진다. 일반적인 예는 흐름 조절을 통해 파이프를 통한 흐름이며, 여기서 레이놀즈 수는 다음과 같이 정의된다.

:

\mathrm{Re} = \frac{\rho u D_\text{H}}{\mu} = \frac{u D_\text{H}}{\nu} = \frac{Q D_\text{H}}{\nu A},

여기서:

기호	설명	단위
D_H	파이프의 수력 지름	m
Q	체적 유량	m³/s
A	파이프의 단면적	m²
u	유체의 평균 속도	m/s
μ	유체의 동점성 계수	Pa·s = N·s/m² = kg/(m·s)
ν	유체의 동점성 계수, ν = μ / ρ	m²/s
ρ	유체의 밀도	kg/m³

이러한 시스템의 경우, 레이놀즈 수가 약 2,040 미만의 임계값 미만일 때 층류가 발생하지만, 전형적으로 1,800에서 2,100 사이의 전환 범위를 갖는다.^[4]

유체 내에 매달린 물체 주변의 흐름과 같이 외부 표면에서 발생하는 유체 시스템의 경우, 물체 주변의 흐름 유형을 예측하기 위해 레이놀즈 수에 대한 다른 정의를 사용할 수 있다. 예를 들어, 유동 유체에 매달린 입자의 경우 입자 레이놀즈 수 Re_p가 사용된다. 파이프 내 흐름과 마찬가지로, 층류는 일반적으로 낮은 레이놀즈 수에서 발생하고, 와류 발생과 같은 난류 흐름 및 관련 현상은 더 높은 레이놀즈 수에서 발생한다.

3. 관수로의 층류 흐름

관수로에서 유체의 유선이 관 축과 평행한 흐름을 층류라고 한다. 관 벽에 가까울수록 유속은 작아지고, 관 중심에서 유속이 가장 커진다. 이는 유체가 관 벽으로부터 마찰 항력을 받기 때문이다. 관 벽으로부터의 거리와 유속의 관계를 식으로 나타낼 수 있으며, 원관로의 층류는 하겐-포아즈유 흐름(Hagen-Poiseuille flow)이라고 불린다.^[1] 난류는 크고 작은 와류가 발생하는 격렬한 흐름이므로, 관계식을 세우기 어렵다.

일반적으로 흐름의 레이놀즈 수가 작을수록, 즉 관의 지름이 작고, 유속이 작고, 밀도가 작고, 점성이 클수록 층류가 되기 쉽다. 반대로 레이놀즈 수가 클수록 난류가 되기 쉽다.

3. 1. 유속 분포

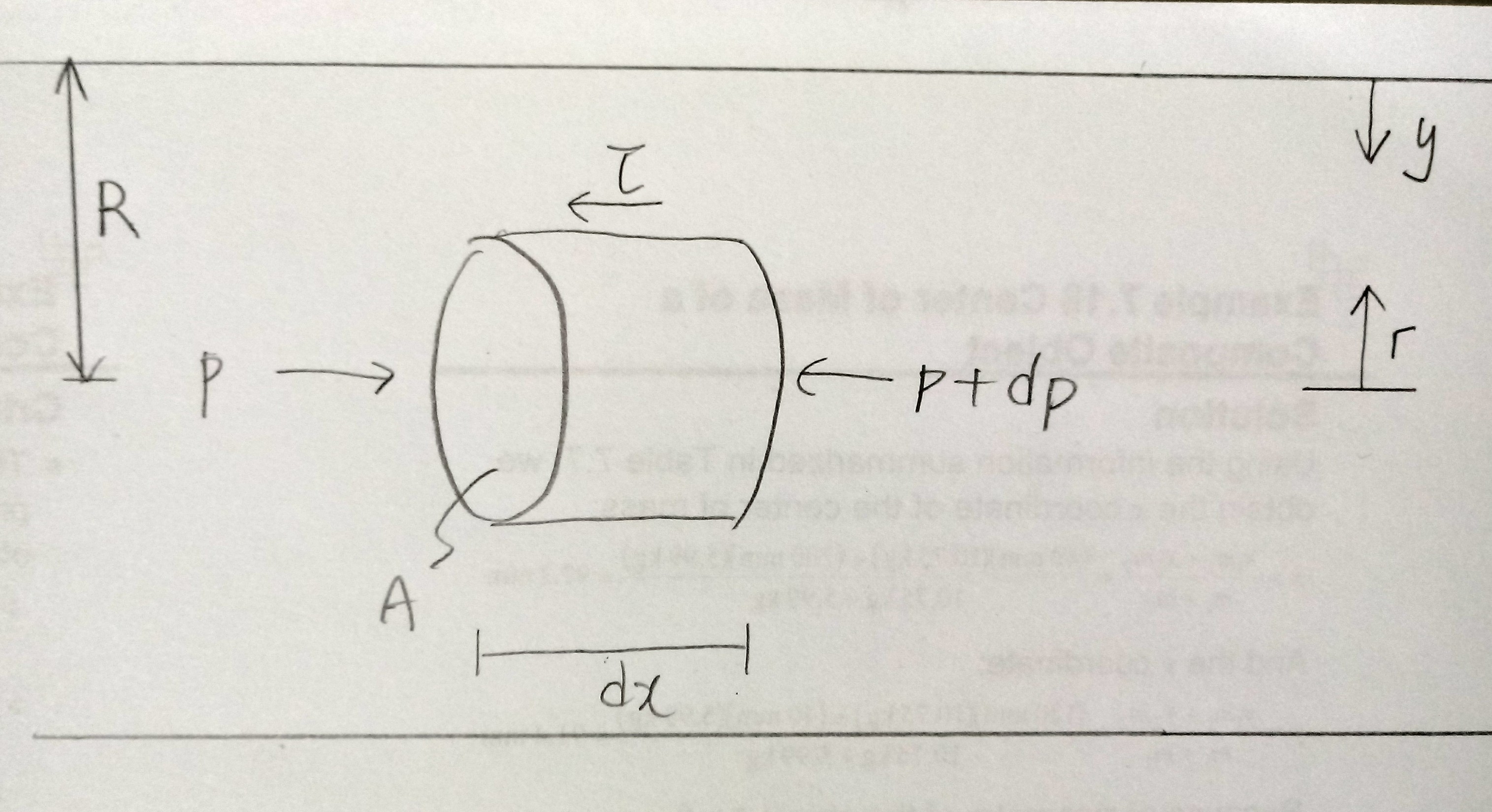
관수로 내 완전 발달한 비압축성 층류 흐름에 대한 유속 분포를 구하기 위해 그림과 같은 미소 요소를 도입한다. 미소 요소에 x 방향으로 운동량 방정식을 적용하면 x 방향으로 가속도가 없으므로 알짜힘도 0이다.

전단 응력에 대해 정리하면 다음과 같다.

:

\tau=-\frac{dp\cdot r}{dx\cdot 2}

층류의 점성 법칙에 의해 다음과 같다.

:

\tau=\mu\frac{du}{dy}

y=R-r이고 dy=-dr이므로 뉴턴의 점성 법칙 즉, 다음과 같다.

:

\tau=-\mu\frac{du}{dr}

전단 응력에 대해 정리한 식과 점성 법칙을 결합하면 다음과 같다.

:

\frac{du}{dr}=\frac{1}{2\mu}\frac{dp}{dx}r

압력 경사 dp/dx는 r과 무관하므로 상수로 취급하고 식을 적분한다.

:

u=\frac{1}{4\mu}\frac{dp}{dx}r^2+C

상수 C를 구하기 위해 관과 접하는 부분(r=R)에서의 유속을 생각해보면 u=0이다. 대입 후 식을 정리하면 포물선의 유속 분포는 다음과 같다.

:

u=-\frac{1}{4\mu}\frac{dp}{dx}R^2\left(1-\frac{r^2}{R^2}\right)

수평관의 경우 다음과 같다.

:

\frac{dp}{dx}=\frac{p_2-p_1}{l}=-\frac{\gamma h_L}{l}

따라서 다음과 같다.

:

u=\frac{\gamma h_L}{4\mu l}R^2\left(1-\frac{r^2}{R^2}\right)

이 식으로 표현되는 층류를 하겐-푸아죄유(Hagen-Poiseuille) 흐름이라고 한다.^[1]

3. 2. 최대 유속 및 평균 유속

관수로에서는 관 중심에서 유속이 최대이다. 즉 r=0일 때, u=u_max이다. 이를 통해 다음 식을 얻는다.^[11]

:

u_{max}=-\frac{1}{4\mu}\frac{dp}{dx}R^2

:

u_{max}=\frac{\gamma h_L}{4\mu l}R^2

따라서 관수로에서 층류 유속 분포 식은 u_max로도 나타낼 수 있다.^[11]

:

u=u_{max}\left( 1-\frac{r^2}{R^2}\right)

평균 유속을 구하기 위해 유량을 먼저 구하면 다음과 같다.

:

\begin{matrix}Q &=& \int_AudA=\int_0^Ru_{max}\left( 1-\frac{r^2}{R^2}\right)2\pi rdr \\&=& \frac{1}{2}u_{max}\pi R^2\end{matrix}

:

V=\frac{Q}{A}=\frac{1}{2}u_{max}

위 식으로부터 관수로의 평균 유속은 관 중심에서 최대 유속의 절반이 됨을 알 수 있다.^[11]

3. 3. 마찰 손실 계수

V=\frac{\gamma h_L}{8\mu l}R^2

이다. R=d/2를 식에 대입하고 손실 수두 h_L에 대해 정리하면 다음과 같다.

:

h_L=\frac{64\mu}{\rho Vd}\frac{l}{d}\frac{V^2}{2g}

이를 Darcy-Weisbach 식과 비교하면 마찰손실계수

f=\frac{64\mu}{\rho Vd}=\frac{64}{Re}

이다. 앞서 마찰손실계수 실험에서 층류의 경우 마찰손실계수는 관의 조도와 상관 없이 레이놀즈 수에만 영향을 받는다고 하였는데, 유도된 식에서도 같은 결론을 얻을 수 있다.

4. 층류의 응용

층류는 점성 액체가 튜브나 파이프를 통해 부드럽게 흐르는 경우에 일반적으로 적용된다. 이 경우, 흐름의 속도는 벽면에서 0에서 용기의 단면 중심을 따라 최대값까지 변화한다. 튜브 내 층류의 유동 프로파일은 흐름을 얇은 원통형 요소로 나누고 점성력을 적용하여 계산할 수 있다.^[5]

항공기 날개 위의 공기 흐름도 층류의 예시이다. 경계층은 날개 표면(및 항공기의 다른 모든 표면) 위에 놓인 매우 얇은 공기 층이다. 공기는 점성을 가지기 때문에 이 공기 층은 날개에 달라붙는 경향이 있다. 날개가 공기 중으로 앞으로 움직일 때, 경계층은 처음에는 에어포일의 유선형 형상 위로 부드럽게 흐른다. 여기서 흐름은 층류이고 경계층은 층류 층이다. 루드비히 프란틀은 1904년에 에어포일에 층류 경계층의 개념을 적용했다.^[6]^[7]

일상생활에서 층류의 예로는 매끄러운 장벽 위로 얕은 물이 천천히, 부드럽고, 광학적으로 투명하게 흐르는 것을 들 수 있다.^[8]

수도꼭지에서 에어레이터 없이 물이 적은 힘으로 나올 때, 처음에는 층류 흐름을 보이지만 중력에 의해 가속되면서 흐름의 레이놀즈 수는 속도에 따라 증가한다. 이로 인해 수도꼭지 하류의 물의 층류 흐름은 난류 흐름으로 전환될 수 있으며, 광학적 투명성이 감소하거나 완전히 사라진다.

층류는 공기의 부피를 분리하거나 공기 중 오염 물질이 특정 영역에 들어가지 못하도록 하는 데 사용된다. 층류 후드는 과학, 전자 및 의학 분야의 민감한 공정에서 오염 물질을 차단하는 데 사용된다. 에어 커튼은 상업 환경에서 가열되거나 냉장된 공기가 출입구를 통과하는 것을 막기 위해 자주 사용된다. 층류 반응기 (LFR)는 화학 반응과 공정 메커니즘을 연구하기 위해 층류를 사용하는 화학 반응기이다. 질병 관리를 위한 쥐의 동물 관리를 위한 층류 설계는 1971년 Beall et al.에 의해 개발되었으며 당시 동구권을 포함하여 전 세계적으로 표준이 되었다.^[9] ^[10]

참조

_[1] 서적 Fluid Mechanics McGraw-Hill
_[2] 서적 Transport Processes and Separation Process Principles http://www.pearsonhi[...] Prentice Hall Professional Technical Reference
_[3] 웹사이트 Real Fluids http://www.efm.leeds[...] University of Leeds 2010-11-23
_[4] 논문 The Onset of Turbulence in Pipe Flow 2011-07
_[5] 웹사이트 Laminar Flow http://hyperphysics.[...] Georgia State University 2010-11-23
_[6] 서적 A History of Aerodynamics and Its Impact on Flying Machines https://books.google[...] Cambridge University Press
_[7] 서적 Laminar flow analysis https://books.google[...] Cambridge University Press
_[8] Youtube Laminar Flow in Nature https://www.youtube.[...] 2016-11-05
_[9] 서적 The Laboratory Rat American College of Laboratory Animal Medicine
_[10] 논문 Gnotobiotic techniques Czechoslovak Society for Microbiology
_[11] 서적

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com