톱니바퀴
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
톱니바퀴는 고대부터 사용된 기계 부품으로, 회전력을 전달하는 데 사용된다. 기원전 4세기 중국에서 가장 오래된 톱니바퀴가 발견되었으며, 안티키테라 기계와 같은 고대 기술에서도 활용되었다. 톱니바퀴는 평행축, 교차축, 엇갈림축 톱니바퀴로 분류되며, 평 톱니바퀴, 헬리컬 기어, 베벨 기어, 웜 기어 등 다양한 종류가 있다. 톱니바퀴의 이빨 모양은 인볼루트 치형과 사이클로이드 치형 등이며, 회전축의 상대적 위치와 톱니의 방향, 모양에 따라 다양한 조합과 기능을 수행한다. 톱니바퀴는 랙 앤 피니언, 유성 기어, 웜 기어 등 다양한 형태로 활용되며, 기어비, 토크, 압력각 등 다양한 용어와 역학적 원리가 적용된다. 현대 물리학에서도 양자 기어 모델과 같은 개념으로 연구되고 있다.
더 읽어볼만한 페이지
- 기계동력전달 - 변속기
변속기는 톱니바퀴를 사용하여 회전수와 방향을 바꾸는 장치이며, 자동차의 주행 조건에 맞춰 엔진의 회전 속도를 조절하고 토크를 변화시키며, 수동변속기와 자동변속기로 구분된다. - 기계동력전달 - 벨트 (기계)
벨트는 축간 동력 전달에 사용되는 기계 요소로, 구조가 간단하고 저렴하며 소음과 진동 감소에 효과적이지만 미끄러짐과 늘어짐이 발생할 수 있고, 평벨트, V벨트, 타이밍 벨트 등이 있다. - 톱니바퀴 - 볼 스크류
볼 스크류는 웜의 회전을 통해 웜 휠을 회전시키는 기어 시스템으로, 속도를 줄이고 토크를 증가시키는 데 효과적이며 다양한 산업 분야 및 정밀 기기에 활용된다. - 톱니바퀴 - 피니언
피니언은 다양한 드라이브트레인 구조에서 사용되는 작은 톱니바퀴를 의미하며, 기어 구동계, 차동 장치, 체인 구동 방식, 랙 앤 피니언 시스템 등에서 활용된다. - 마찰학 - 베어링
베어링은 회전 부품의 마찰을 줄여 효율성을 높이는 기계 요소로, 다양한 구조(미끄럼, 구름, 유체, 자기)와 하중, 윤활 방식에 따라 분류되며 산업 전반에 걸쳐 널리 사용되고, 수명은 사용 조건에 따라 달라진다. - 마찰학 - 마모
마모는 재료 표면이 마찰, 충격, 부식 등으로 손상되거나 제거되는 현상으로, 여러 마모 메커니즘이 복합적으로 작용하며, 마모량은 다양한 요인에 영향을 받고, 윤활제 사용 등으로 감소시킬 수 있고, 표준 시험법으로 저항성을 평가하며, 여러 방법으로 측정이 가능하다.
| 톱니바퀴 | |
|---|---|
| 개요 | |
| 종류 | 회전하는 원형 기계 부품 |
| 특징 | 이빨이 있어 다른 이빨과 맞물림 |
| 사용 | 동력 전달 장치 |
| 다른 용어 | 톱니바퀴, 기어 |
| 기어의 종류 | |
| 스퍼 기어 | 가장 일반적인 형태, 축에 평행한 이빨 |
| 헬리컬 기어 | 이빨이 축에 대해 비스듬함, 더 부드러운 작동 |
| 베벨 기어 | 축이 교차하는 경우 사용, 원뿔 모양 |
| 웜 기어 | 큰 감속비 가능 |
| 랙 앤 피니언 | 회전 운동을 직선 운동으로 변환 |
| 유성 기어 | 복잡한 구조, 다양한 변속비 가능 |
| 기어의 작동 원리 | |
| 기어비 (r) | = r = }} (T는 이의 수, N은 회전수) |
| 회전 속도 비 | = = }} (ω는 각속도) |
| 동력 전달 | 맞물린 기어를 통해 회전 운동과 토크 전달 |
| 기어의 용도 | |
| 자동차 변속기 | 엔진의 회전력을 바퀴에 전달, 속도 조절 |
| 시계 | 정밀한 시간 측정 |
| 자전거 | 페달링 힘을 바퀴에 전달 |
| 산업 기계 | 다양한 기계 장치에서 동력 전달 |
| 기어 관련 용어 | |
| 모듈 | 기어의 크기를 나타내는 단위 |
| 피치 원 | 기어가 맞물리는 기준 원 |
| 백래시 | 기어 사이에 존재하는 약간의 틈새 |
| 기타 | |
| 재료 | 강철, 황동, 플라스틱 등 다양한 재료 사용 |
| 윤활 | 원활한 작동을 위해 윤활유 사용 |
| 제조 | 절삭 가공, 주조, 사출 성형 등 다양한 방법 사용 |
2. 역사
톱니바퀴는 회전축의 상대적 위치, 톱니의 방향, 톱니의 모양 등 다양한 기준으로 분류할 수 있다.
현존하는 가장 오래된 톱니바퀴는 기원전 4세기 중국 전국 시대의 유물에서 발견되었으며, 허난성 낙양박물관에 보존되어 있다.[14]
유럽에서는 기원전 330년경 아리스토텔레스가 풍차의 톱니바퀴를 언급하며 회전 방향의 반전을 기록했다. 비잔티움의 필론은 기어를 이용해 물을 퍼올리는 장치를 사용했다.[15] 기원후 50년경 알렉산드리아의 헤론의 작품에 기어가 등장하며,[16] 이는 기원전 3세기 프톨레마이오스 왕조 알렉산드리아 도서관의 역학에서 비롯되었고, 아르키메데스에 의해 발전되었다.[17] 유럽에서 가장 오래된 기어는 안티키테라 기계에서 발견되었으며, 기원전 150년에서 100년 사이에 제작된 것으로 추정된다.[18][19][20]
중국 기술자 마준(~265)은 남쪽을 가리키는 수레를 만들었는데, 여기에는 수레가 회전해도 지시계 방향을 유지하는 차동기어가 사용되었다.[21]
6세기 초 비잔틴 제국에서는 달의 위상, 월일, 황도대에서 태양과 달의 위치를 보여주는 복잡한 달력 장치가 발명되었다.[22][23] 1221년경 이스파한에서는 달의 황도대 위치와 위상 등을 보여주는 기어식 천구의가 만들어졌다.[24]
웜 기어는 13세기-14세기 인도 아대륙에서 롤러 면방기에 사용되었다.[25] 조반니 돈디 델로로지오는 1348년에서 1364년 사이에 아스트라리움이라는 복잡한 천문 시계를 제작했는데, 여기에는 태양, 달, 5개 행성의 위치와 종교 축제일을 보여주는 기어 장치가 있었다.[26] 1386년에 만들어진 솔즈베리 대성당 시계는 현재까지 작동하는 가장 오래된 기계식 기어 시계이다.
1720년 영국의 시계 제작자 조셉 윌리엄슨은 차동기어를 사용했다.
캠브리지 대학교 연구진은 2013년 ''Issus coleoptratus''라는 곤충의 뒷다리에서 톱니바퀴 구조를 발견했다. 이 곤충은 톱니바퀴를 이용해 뒷다리를 정확하게 동기화하여 점프한다.[63][64][65] ''I. coleoptratus''의 각 다리에는 400마이크로미터 길이의 이빨이 있으며, 10~12개의 완전히 맞물리는 스퍼형 기어 이빨이 있다.[67]
비트루비우스는 『건축에 관하여』에서 물레방아에 대해 논했으며, 수직 회전 동력을 수평 회전으로 변환하는 랜턴 기어는 1세기경 로마 제국에서 보급되어 18세기 말까지 사용되었다.[78] 전금속제 톱니바퀴는 11~12세기경에 등장했지만, 주로 시계와 같은 정밀 기기에 사용되었다.[78]
3. 종류
이 외에도 베벨 기어, 랙 앤 피니언, 유성 기어, 웜 기어, 하이포이드 기어, 페이스 기어, 비원형 톱니바퀴 등 다양한 종류의 톱니바퀴가 있다.
3. 1. 회전축의 상대적 위치에 따른 분류

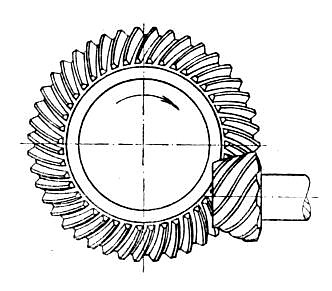

톱니바퀴는 회전축의 상대적 위치에 따라 크게 세 가지로 분류된다.3. 2. 톱니의 방향에 따른 분류
Spur gear영어라고도 불리는 평 톱니바퀴는 톱니가 회전축과 평행한 가장 기본적인 형태의 톱니바퀴이다.[70] 제작이 쉽기 때문에 동력 전달용으로 가장 많이 사용된다. 톱니바퀴끼리 바깥쪽에서 맞물리는 외접 톱니바퀴와, 작은 톱니바퀴가 원통의 안쪽에 톱니가 설치된 큰 톱니바퀴에 안쪽에서 맞물리는 내접 톱니바퀴가 있다.[70] 큰 톱니바퀴와 작은 톱니바퀴를 조합할 때, 큰 것을 '''기어''', 작은 것을 '''피니언'''이라고 한다. 피니언과 조합되는 큰 톱니바퀴는 바깥쪽 톱니바퀴뿐만 아니라 안쪽 톱니바퀴나 랙 앤 피니언과 같이 직선 형태로 톱니를 배치한 랙(rack영어)과도 조합된다.[70]

Helical gear영어라고도 불리는 헬리컬 톱니바퀴는 평 톱니바퀴의 톱니를 축에 대해 비스듬하게 잘라서 나선 모양으로 만든 톱니바퀴이다.[73] 톱니의 접촉이 분산되므로 소음이 적고 토크의 변동이 적다. 토크가 걸리면 추력이 발생하므로 스러스트 베어링이 필요하다.[73]
Herringbone gear영어 또는 '''이중 나선형 기어'''라고도 불리는 산형 톱니바퀴는 같은 경사각으로 엇갈리는 방향의 헬리컬 톱니바퀴 두 개를 조합한 형태로, 헬리컬 톱니바퀴의 축 방향으로 발생하는 힘을 서로 상쇄하는 구조의 톱니바퀴이다.[73]
안쪽 톱니바퀴는 평 톱니바퀴의 일종으로, 원통의 안쪽에 톱니가 있는 톱니바퀴이다. 안쪽에 물리므로 작은 지름의 톱니바퀴와만 조합할 수 있다. 유성기어장치와 같이 이 톱니바퀴가 없으면 성립하지 않는 구조도 있다.
3. 3. 톱니의 모양에 따른 분류
톱니바퀴의 이빨 모양은 수학적 계산으로 구해지는 곡선이며, 톱니바퀴를 제작하고 이용하는 관점에서는 치형곡선(歯形曲線)이라고 한다. 동력 전달용 톱니바퀴로는 인볼루트곡선과 사이클로이드곡선 두 종류가 기본으로 여겨지지만, 일반적으로는 인볼루트곡선이 사용된다.[76]
; 인볼루트 치형
: 인볼루트곡선으로 만들어진 치형으로, 톱니바퀴의 중심 거리가 약간 변해도 맞물림이 정확하게 유지된다.[76] 호브반으로 쉽게 제작할 수 있고, 미끄러짐도 적기 때문에 일반적으로 많이 사용된다.
; 사이클로이드 치형
: 사이클로이드곡선으로 만들어진 치형으로, 인볼루트 치형과 비교하면 이빨의 간섭과 미끄러짐이 적고, 미끄러짐이 더욱 균일하지만 제작이 어렵다.[76] 시계의 기구에 사용된다.
; 트로코이드 치형
: 트로코이드곡선으로 만들어진 치형으로, 내접톱니바퀴펌프에 사용된다.
3. 4. 기타
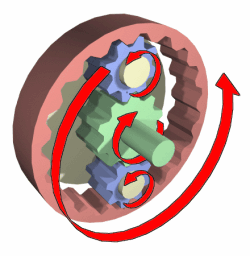
4. 톱니바퀴의 역학
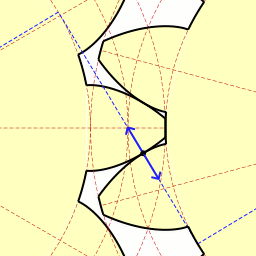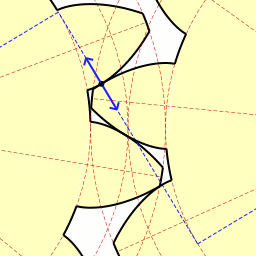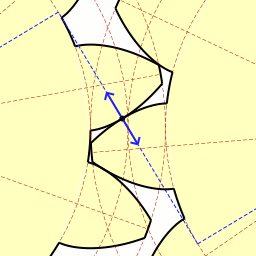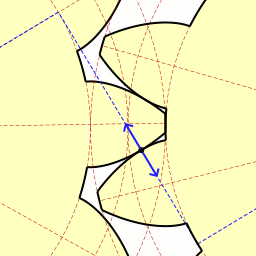
맞물리는 톱니바퀴의 톱니면에 작용하는 힘(법선하중)은 항상 피치점을 향하는 방향으로 작용하며, 그 작용선은 인벌류트 톱니바퀴에서는 기초원의 공통접선(가상벨트)과 일치한다.[1] 피치점 이외의 맞물림점에서는 톱니면이 상대적으로 미끄러지며 접촉하므로 톱니면의 공통 접선 방향으로 마찰력이 작용하지만, 그 크기는 대략 법선 하중의 1/10 정도이다.[1] 이 마찰력의 방향은 톱니면의 서로 마찰되는 방향에 따라서 정해지며, 맞물림의 시점(始點)으로부터 피치점에 접근하는 동안 종동바퀴(從動車)의 회전을 방해하고, 피치점에서부터 멀어지는 동안은 회전을 돕도록 작용한다.[1] 따라서 맞물림점의 이동에 따라서 힘의 크기가 다소 변화하고, 또 맞물림의 쌍수가 2쌍 이상이 되면 각 맞물림점에 하중이 배분된다.[1]
톱니는 하중에 의해서 부러지지 않도록 충분히 튼튼하게 만들어야 하며, 동시에 톱니면이 빨리 닳지 않도록 맞물림점에 생기는 응력(접촉응력)이 너무 커지지 않도록 설계해야 한다.[1] 마찰력을 생략하고 생각하면, 법선하중과 같은 크기의 하중이 축받이에 작용한다.[1] 법선하중의 작용선이 중심선과 이루는 각의 여각(餘角) α를 압력각이라 한다.[1] 전달토크 Ti(i=1,2)를 일정하다고 하고, 피치원 반경을 Ri로 하면, 법선하중 FN은 다음과 같이 나타낼 수 있다.[1]
: FN = Ti / RiCosα (RiCosα = 기초원 반경)
압력각 α가 클수록 축받이 압력이 커지기 때문이다.[1] 압력각의 크기는 대략 14.5° ~ 30°의 범위를 갖는다.[1]
가장 일반적인 구성에서 두 톱니바퀴의 회전축은 평행하며, 일반적으로 크기는 두 축 사이의 한 점 근처에서 접촉하도록 설계된다. 이 구성에서 두 톱니바퀴는 반대 방향으로 회전한다. 때때로 축은 평행하지만 한 톱니바퀴가 다른 톱니바퀴 안에 중첩되기도 한다. 이 구성에서는 두 톱니바퀴 모두 같은 방향으로 회전한다. 두 톱니바퀴를 축에 수직인 허상의 평면으로 자르면, 한 톱니바퀴의 각 부분은 다른 톱니바퀴의 해당 부분과만 상호 작용한다. 따라서 3차원 기어 트레인은 평평하고 무한히 얇은 톱니바퀴들의 집합, 즉 본질적으로 2차원 톱니바퀴로 이해될 수 있다.
서로 다른 톱니 수의 톱니바퀴를 조합하여 감속 또는 증속에 사용한다. 웜기어를 제외한 두 개의 톱니바퀴가 맞물리는 경우, 회전 각도 및 각속도의 비는 톱니 수의 비의 역수가 된다. 토크의 비는 마찰력을 제외하면 지렛대의 원리에 따라 피치원 반지름의 비가 된다. 톱니 수의 비와 피치원 지름의 비는 같으므로, 구동 기어를 D, 종동 기어를 P로 하여 식으로 나타내면 다음과 같다.
- j=1/u=P의 톱니 수/D의 톱니 수=P의 피치원 지름/D의 피치원 지름=D의 회전 각도/P의 회전 각도=D의 각속도/P의 각속도=P의 토크/D의 토크
세 개 이상의 톱니바퀴가 순서대로 맞물리는 경우, 첫 번째와 마지막 톱니바퀴의 비는 첫 번째와 마지막 톱니바퀴가 직접 맞물리는 경우와 동일하며, 중간 톱니바퀴의 톱니 수와는 관계가 없다.(세 개의 평기어로 입력과 출력의 회전 방향을 같게 하는 경우 등) 구동 기어의 톱니 수가 종동 기어의 톱니 수보다 작은 경우 감속이 되어 토크가 증가하고, 반대의 경우 증속이 되어 토크가 감소한다.
- P의 토크 × P의 회전 각도 = D의 토크 × D의 회전 각도
- P의 토크 × P의 각속도 = D의 토크 × D의 각속도
위의 관계식을 통해 마찰 손실을 제외하면 에너지 및 일률은 변하지 않음을 알 수 있다. 예를 들어, 톱니 수 90의 큰 톱니바퀴와 톱니 수 20의 작은 톱니바퀴가 맞물리는 경우, 작은 톱니바퀴의 각속도는 큰 톱니바퀴의 4.5배, 큰 톱니바퀴의 토크는 작은 톱니바퀴의 4.5배가 되며, 작은 톱니바퀴가 3회전하면 큰 톱니바퀴는 240도 회전한다.
5. 이끊기법과 전위치차
톱니바퀴의 톱니는 주조로 만들기도 하지만, 흔히 날붙이로 톱니홈 부분을 깎아서 만든다. 톱니 수가 적을 때는 톱니의 뿌리 부분이 약해지므로, 절하(切下)라고 해서 날붙이를 알맞게 후퇴시켜 톱니를 깎는 경우가 많다. 이것을 정의 전위라고 한다. 이렇게 하면 톱니는 밑뿌리가 굵어지고, 인벌류트의 기초원으로부터 떨어진 부분을 이용하므로, 강도나 맞물림 성능이 좋아진다. 톱니 수가 많은 톱니바퀴는 날을 전진시켜(부의 전위) 톱니를 깎기도 한다. 이렇게 깎은 톱니는 올바르게 맞물리지만, 중심 거리나 맞물림 압력각은 표준적인 것과는 달라진다. 이를 전위 톱니바퀴라고 한다. 작은 톱니바퀴를 정전위하고 큰 톱니바퀴를 같은 양만큼 부전위하면, 중심 거리와 맞물림 압력각은 표준 톱니바퀴와 같아지지만, 톱니의 높이는 양쪽 바퀴가 서로 같지 않다. 전위량을 적절하게 선택하면 톱니의 강도나 성능을 크게 개선할 수 있으므로, 현재의 톱니바퀴는 대부분 전위 톱니바퀴로 되어 있다.[48]
6. 톱니바퀴의 조합
원동축과 종동축 사이에 톱니바퀴를 여러 방식으로 조합하여 필요한 운동을 전달할 수 있는데, 이를 톱니바퀴열이라고 한다. 예를 들어, 톱니바퀴 축을 고정 지지틀로 지탱하고 여러 개의 톱니바퀴를 계속해서 맞물리게 할 수 있다. 이때 톱니바퀴의 톱니 수를 ${\displaystyle N}$, 회전 속도를 ${\displaystyle n}$으로 나타내면, 톱니바퀴비는 ${\displaystyle {\frac {N_{1}}{n_{1}}}={\frac {N_{2}}{n_{2}}}={\frac {N_{3}}{n_{3}}}=...}$ 와 같이 표현된다.
중간 톱니바퀴를 사용한 경우에는 ${\displaystyle {\frac {N_{1}}{n_{1}}}={\frac {N_{4}}{n_{4}}}}$ 가 되고, 중간 톱니바퀴의 톱니 수는 톱니바퀴비와 관계가 없다. 그러나 톱니바퀴의 개수가 홀수냐 짝수냐에 따라 종동축의 회전 방향이 원동축과 같거나 반대가 된다.
톱니바퀴의 조합을 변화시켜 원동축의 일정한 회전 속도에 대해 종동축의 회전 속도를 여러 범위로 변환하는 장치를 톱니바퀴 변속 장치라고 한다. 종동축의 회전 속도가 만드는 수열을 속도 열이라 하며, 공작 기계나 자동차 등에는 등비수열이 쓰이는 경우가 많고, 계산기 등에는 등차수열도 사용된다.
서로 다른 이빨 수의 기어를 조합하여 감속 또는 증속에 사용한다. 웜기어를 제외하고 두 개의 기어가 맞물리는 경우, 회전 각도 및 각속도의 비는 이빨 수의 비의 역수가 된다. 토크의 비는 마찰력을 제외하면 지렛대의 원리에 따라 피치원 반지름의 비와 같다. 이빨 수의 비와 피치원 지름의 비는 같으므로, '''구동 기어를 D''', '''종동 기어를 P'''로 하여 식으로 나타내면 다음과 같다.
- j=1/u=P의 이빨 수/D의 이빨 수=P의 피치원 지름/D의 피치원 지름=D의 회전 각도/P의 회전 각도=D의 각속도/P의 각속도=P의 토크/D의 토크
세 개 이상의 기어가 순서대로 맞물리는 경우, 첫 번째와 마지막 기어의 비는 첫 번째와 마지막 기어가 직접 맞물리는 경우와 동일하며, 중간 기어의 이빨 수와는 관계가 없다. (세 개의 평기어로 입력과 출력의 회전 방향을 같게 하는 경우 등)
- 구동 기어의 이빨 수 < 종동 기어의 이빨 수 인 경우 감속이 되어 토크가 증가하고, 반대의 경우 증속이 되어 토크가 감소한다.
- P의 토크 × P의 회전 각도 = D의 토크 × D의 회전 각도
- P의 토크 × P의 각속도 = D의 토크 × D의 각속도 가 되어, 마찰 손실을 제외하면 에너지 및 일률은 변하지 않는다.
예를 들어, 이빨 수 90의 큰 기어와 이빨 수 20의 작은 기어가 맞물리는 경우, 작은 기어의 각속도는 큰 기어의 4.5배, 큰 기어의 토크는 작은 기어의 4.5배가 되며, 작은 기어가 3회전하면 큰 기어는 240도 회전한다.
7. 톱니바퀴의 활용
톱니바퀴는 매우 다양한 분야에서 활용되고 있다.
| 시기 | 내용 |
|---|---|
| 기원전 4세기 | 중국 전국 시대 유물에서 톱니바퀴 발견 (낙양박물관 보존).[14] |
| 기원전 330년경 | 아리스토텔레스가 풍차의 톱니바퀴 언급, 회전 방향 반전 관찰. 비잔티움의 필론이 기어를 이용한 물을 퍼올리는 장치 사용.[15] |
| 기원전 3세기 | 프톨레마이오스 시대 이집트 알렉산드리아 도서관에서 기어 사용, 아르키메데스에 의해 크게 발전.[17] |
| 기원전 150년 ~ 100년 사이 | 안티키테라 기계 제작 추정. 태양, 달, 행성 위치 계산 및 일식 예측에 사용.[18][19][20] |
| 200~265년경 | 중국 기술자 마준이 남쪽을 가리키는 수레 제작, 차동 기어 사용.[21] |
| 6세기 초 | 비잔틴 제국에서 달의 위상, 월일 등 보여주는 복잡한 달력 장치 발명.[22][23] |
| 725년 | 중국에서 기어식 기계식 물시계 제작. |
| 1221년경 | 이스파한에서 달의 황도대 위치와 위상 등 보여주는 기어식 천구의 제작.[24] |
| 13세기-14세기 | 인도 아대륙에서 웜 기어가 롤러 면방기에 사용하기 위해 발명.[25] |
| 1348년 ~ 1364년 | 조반니 돈디 델로로지오가 아스트라리움 제작. 태양, 달, 5개 행성 위치와 종교 축제일 표시.[26] |
| 1386년 | 솔즈베리 대성당 시계 제작 (세계에서 가장 오래된 작동하는 기계식 기어 시계). |
| 1720년 | 영국 시계 제작자 조셉 윌리엄슨이 차동 기어 사용. |
| 1957년 (최초 발견) 2013년 (기능 규명) | Issus coleoptratus 곤충 뒷다리에서 자연 톱니바퀴 발견. 매미충 뒷다리에서 발견, 캠브리지 대학교에서 기능 규명.[63][64][65] 약충 형태에서만 발견, 성충 시 사라짐.[66] I. coleoptratus 다리에 10~12개 맞물리는 스퍼형 기어 이빨, 점프 시 다리 동기화, 요(Yaw) 회전 방지.[67][68][69][64] |
8. 톱니바퀴 관련 용어
| 용어 | 설명 |
|---|---|
| 이(tooth) | 톱니바퀴의 돌출 부분.[28][29] |
| 이수 () | 톱니의 개수. |
| 피치원(pitch circle) | 맞물리는 톱니바퀴의 기준이 되는 원. 기어가 맞물리는 위치에서 중심까지의 거리의 두 배가 피치원 지름()이다. |
| 이면(tooth surface) | 톱니의 윤곽. 피치원보다 바깥쪽은 이끝면(tooth face), 안쪽은 이뿌리면(tooth flank)이다. |
| 이끝원(addendum circle) | 톱니 끝 부분을 지나고 피치원과 동심인 원. 이끝원 지름은 이다. |
| 이뿌리원(dedendum circle, root circle) | 톱니 뿌리 부분을 지나고 피치원과 동심인 원. 이뿌리원 지름은 이다. |
| 이끝 높이(addendum) () | 이끝원 반지름과 피치원 반지름의 차이. |
| 이뿌리 높이(dedendum) () | 피치원 반지름과 이뿌리원 반지름의 차이. |
| 전체 이 높이(whole depth) () | 이끝 높이와 이뿌리 높이의 합 (). |
| 정극(top clearance) | 이뿌리 높이 와 맞물리는 기어의 이끝 높이 와의 차이 (). |
| 피치(pitch)·원주 피치(circular pitch) () | 피치원상의 한 톱니의 점과 이웃하는 톱니의 점 사이의 거리를 피치원을 따라 측정한 것 (). |
| 법선 피치(normal pitch) | 인벌류트 치형에서 인벌류트의 법선이 이웃하는 인벌류트에 의해 잘리는 길이. |
| 이폭(face width) | 기어의 축 방향으로 측정한 톱니의 길이. |
| 이두께(tooth thickness) () | 피치원상에서 측정한 톱니의 두께. |
| 이홈 너비(space thickness) () | 피치원상에서 측정한 톱니와 이웃하는 톱니 사이의 틈새 길이. |
| 백래시(backlash) | 맞물리는 톱니 사이의 틈새. 두 개의 맞물리는 기어에서 서로의 피치원 사이에 있는 틈새로, 톱니 양면의 접촉을 방지하고 성능 저하를 막기 위해 마련된다. |
| 모듈(module) | 톱니의 크기를 나타내는 규격 값. 피치원 지름을 톱니의 수로 나눈 값(피치원 지름 / 잇수)이다. 일반적인 표준 치수의 이를 평치(full depth tooth)라 하며, 평치에서는 이끝 높이와 모듈을 같게 한다. |
| 압력각(Pressure angle) | 톱니에 작용하는 힘의 방향과 톱니바퀴 중심을 연결하는 선 사이의 각도. |
| 크라우닝(crowning) | 기어가 서로 맞물릴 때, 전반적으로 매끄러움을 더함으로써 상대 이를 단단히 맞물리게 하는 것. |
| 속도비 () | (구동 기어의 이수 / 종동 기어의 이수) (종동 기어의 각속도 / 구동 기어의 각속도) |
| 전달비 () | 전달비는 속도비의 역수 (). |
9. 톱니바퀴와 관련된 현대 물리학
19세기에 제임스 클러크 맥스웰은 자기장 선이 비압축성 유체의 회전하는 관으로 구성된 전자기 모델을 개발했다. 맥스웰은 기어 톱니바퀴를 사용하여 회전하는 자기장 선과 반대 방향으로 입자가 회전하는 것을 전류로 설명했고 이를 "유휴 톱니바퀴(idle wheel)"라고 불렀다.[60]
최근에는 양자 물리학이 "양자 기어" 모델을 사용한다. 여러 개의 기어는 인공적으로 제작된 나노 기계 장치나 고리 분자 그룹과 같은 여러 다른 시스템의 모델 역할을 할 수 있다.[61]
삼파장 가설(three wave hypothesis)은 파동-입자 이중성을 베벨 기어에 비유한다.[62]
참조
[1]
웹사이트
Definition of "gear"
https://www.merriam-[...]
2018-09-20
[2]
웹사이트
Definition of "gear"
https://www.oxfordle[...]
2024-07-27
[3]
웹사이트
Definition of "gearwheel"
https://www.collinsd[...]
2024-07-27
[4]
웹사이트
Definition of "gearwheel"
https://www.merriam-[...]
2018-09-20
[5]
웹사이트
Definition of "gearwheel"
https://www.oxfordle[...]
2024-07-27
[6]
웹사이트
Definition of "cog"
https://www.oxfordle[...]
2024-07-29
[7]
웹사이트
Definition of "cog"
https://www.merriam-[...]
2024-07-29
[8]
웹사이트
Definition of "cog"
https://dictionary.c[...]
2024-07-29
[9]
웹사이트
Definition of "cog"
https://www.collinsd[...]
2024-07-29
[10]
논문
Reconfigurable multi-component micromachines driven by optoelectronic tweezers
[11]
간행물
MY GEAR is Bigger than YOUR GEAR: Industry Battles it Out for World’s Largest Gear Title
https://www.geartech[...]
2013
[12]
웹사이트
Levers - Moments, levers and gears - AQA - GCSE Physics (Single Science) Revision - AQA - BBC Bitesize
https://www.bbc.co.u[...]
1970-01-01
[13]
웹사이트
Transmission Basics
http://auto.howstuff[...]
2005-04-27
[14]
서적
On the Origin of Clockwork, Perpetual Motion Devices, and the Compass
http://www.gutenberg[...]
[15]
웹사이트
Gears from Archimedes, Heron and Dionysius
https://www.hellenic[...]
2023-11-21
[16]
문서
(정보 부족)
[17]
논문
Gearing in the Ancient World
[18]
웹사이트
The Antikythera Mechanism Research Project: Why is it so important?
http://www.antikythe[...]
2011-01-10
[19]
웹사이트
World's first computer, the Antikythera Mechanism, 'started up' in 178 B.C., scientists claim
https://www.livescie[...]
2022-04-14
[20]
웹사이트
An Ancient Greek Astronomical Calculation Machine Reveals New Secrets
https://www.scientif[...]
[21]
서적
Science and Civilization in China: Volume 4, Part 2
Caves Books, Ltd
[22]
웹사이트
vertical dial British Museum
https://www.britishm[...]
[23]
웹사이트
The Portable Byzantine Sundial Calendar: The Second Oldest Geared Mechanism in Existence
https://www.thearcha[...]
[24]
웹사이트
Astrolabe By Muhammad Ibn Abi Bakr Al Isfahani
https://www.mhs.ox.a[...]
[25]
서적
Economic History of Medieval India, 1200-1500
https://books.google[...]
Pearson Education
[26]
웹사이트
Giovanni Dondi's Astrarium, 1364 cabinet
https://www.cabinet.[...]
[27]
웹사이트
gear (n.)
https://www.etymonli[...]
2020-02-13
[28]
웹사이트
Etymology 1: Cog (noun)
https://en.wiktionar[...]
2019-07-29
[29]
웹사이트
cog (n.)
https://www.etymonli[...]
2020-02-13
[30]
서적
A Treatise on Gear Wheels
https://archive.org/[...]
George B. Grant
[31]
웹사이트
Plastic gears are more reliable when engineers account for material properties and manufacturing processes during design.
http://motionsystemd[...]
[32]
서적
Dudley's Handbook of Practical Gear Design and Manufacture
http://download.drge[...]
CRC Press, an imprint of Taylor & Francis Group
[33]
간행물
Materials Matter
http://www.gearsolut[...]
2014-08
[34]
웹사이트
Gear Types
http://gemini.tntech[...]
Tennessee Tech University, Department of Mechanical Engineering, ME 362 lecture notes
[35]
서적
Geometry and the Imagination
Chelsea
[36]
서적
[37]
웹사이트
How Gears Work
http://science.howst[...]
2000-11-16
[38]
서적
Machinery's Handbook
https://archive.org/[...]
Industrial Press
[39]
서적
[40]
서적
Theory of Machines
S.CHAND
[41]
웹사이트
Motion System Design
2024-05
[42]
서적
[43]
웹사이트
Helical gears
http://www.roymech.c[...]
2009-06-15
[44]
서적
[45]
서적
[46]
서적
[47]
서적
[48]
간행물
Gear Nomenclature, Definitions of Terms with Symbols
American Gear Manufacturers Association
[49]
학술지
The Cosmos in the Antikythera Mechanism
https://dlib.nyu.edu[...]
Institute for the Study of the Ancient World
2012-02
[50]
서적
[51]
학술지
Algorithms for Involute and Octoidal Bevel-Gear Generation
[52]
서적
[53]
논문
Diss. Hünecke, TU Dresden
[54]
특허
Gear with magnetic couple
2011
[55]
표준
Gears – Cylindrical Involute Gears and Gear Pairs – Concepts and Geometry
International Organization for Standardization
[56]
서적
Konstruktionselement och maskinbyggnad
[57]
웹사이트
W. M. Berg Gear Reference Guide
http://www.wmberg.co[...]
[58]
서적
Machinery's Handbook
Industrial Press
[59]
웹사이트
Elements of metric gear technology
http://qtcgears.com/[...]
[60]
서적
Innovation in Maxwell's Electromagnetic Theory: Molecular Vortices, Displacement Current, and Light
University of Chicago Press
[61]
학술지
Quantum Gears: A Simple Mechanical System in the Quantum Regime
[62]
학술지
Does the Three Wave Hypothesis Imply Hidden Structure?
http://redshift.vif.[...]
[63]
학술지
Bau und Funktion des Sprungapparates von ''Pyrilla perpusilla'' WALKER (Homoptera - Fulgoridae)
1957
[64]
학술지
Interacting Gears Synchronize Propulsive Leg Movements in a Jumping Insect
https://research-inf[...]
2013-09-13
[65]
웹사이트
The First Gear Discovered in Nature
https://www.popularm[...]
2013-09-12
[66]
웹사이트
Insects Use Gears in Hind Legs to Jump
https://news.nationa[...]
2013-09-12
[67]
웹사이트
This Insect Has The Only Mechanical Gears Ever Found in Nature
https://getpocket.co[...]
2013-09-12
[68]
뉴스
The first-ever naturally occurring gears are found on an insect's legs
https://www.theverge[...]
2013-09-12
[69]
웹사이트
Functioning 'mechanical gears' seen in nature for the first time
https://phys.org/new[...]
PHYS.ORG, Cambridge University
[70]
문서
大西1997
[71]
문서
摩擦面に同じ金属を使う事を「ともがね」と言い、歯車に限らず摩擦面に用いるのは基本的に避けるのがセオリーである。これは摩擦・摩耗の分野では常識であり、トライボロジーが発展する前からの経験則から知られていた事象である。
[72]
문서
三輪自動車で駆動輪が一つのものを除く。
[73]
문서
大西1997 pp11-3
[74]
웹사이트
無制限の可動範囲を有する回転3自由度の球状歯車機構の開発
https://shingi.jst.g[...]
国立研究開発法人科学技術振興機構
2020-10-06
[75]
웹사이트
【有料記事】SNS沸騰の「球状歯車」 全方向無制限駆動で人型ロボットに衝撃
https://xtech.nikkei[...]
日本経済新聞社|日経クロステック
2021-07-29
[76]
문서
大西1997 pp11-1
[77]
논문
Planetary Gears
[78]
서적
作ること使うこと:生活技術の歴史・民俗学的研究
藤原書店
2019
[79]
뉴스
“歯車”を使ってジャンプする昆虫
https://natgeo.nikke[...]
ナショナルジオグラフィック
2013-09-13
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com

