투표의 역설
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
투표의 역설은 다수결 투표 방식에서 발생하는 모순으로, 13세기에 라몬 률에 의해 처음 발견되었고, 18세기 말 콩도르세 후작에 의해 재발견되었다. 이 역설은 다수결 원칙에 따라 투표 결과가 순환적인 모습을 보이며, 어떤 대안을 선택하든 다수의 유권자가 선호하는 다른 대안이 존재하여 논리적 모순에 빠질 수 있음을 보여준다. 콩도르세 역설은 유권자 선호도에 따라 발생 확률이 달라지며, 실제 선거에서는 드물게 나타난다. 이 역설은 의회 절차에서 결과 조작 가능성을 시사하며, 콩도르세 투표 방법과 같은 대안을 제시하기도 한다.
더 읽어볼만한 페이지
- 민주주의 이론 - 자유민주주의
자유민주주의는 국민의 자유와 권리 보호를 위한 대의 민주주의 체제로, 선거로 선출된 대표가 권력을 행사하며 입헌주의에 따라 기본권이 보장되지만, 다수의 횡포나 금권 정치 등의 비판도 존재한다. - 민주주의 이론 - 애로의 불가능성 정리
애로의 불가능성 정리는 3개 이상의 선택지에서 약한 파레토, 무관한 대안으로부터의 독립성, 비독재성을 모두 만족하는 사회 후생 함수는 존재하지 않음을 증명한 정리이다. - 의사결정의 역설 - 애로의 불가능성 정리
애로의 불가능성 정리는 3개 이상의 선택지에서 약한 파레토, 무관한 대안으로부터의 독립성, 비독재성을 모두 만족하는 사회 후생 함수는 존재하지 않음을 증명한 정리이다. - 의사결정의 역설 - 몬티 홀 문제
몬티 홀 문제는 세 개의 문 중 하나를 선택한 후 진행자가 상품이 없는 문을 열어 보여줄 때, 선택을 바꾸는 것이 유리한지를 묻는 확률 문제로, 직관과 달리 선택을 바꾸는 것이 당첨 확률을 높이는 전략임을 보여주는 확률 역설이며, 의사 결정 방식에 대한 통찰을 제공한다. - 역설 - 모라벡의 역설
모라벡의 역설은 인간에게는 쉽지만 기계에게는 어려운 감각 운동 능력과, 인간에게는 어렵지만 기계에게는 쉬운 추상적 사고 능력 간의 역전 현상을 설명하며, 이는 인공지능 개발의 어려움과 새로운 접근 방식의 필요성을 시사한다. - 역설 - 슈뢰딩거의 고양이
슈뢰딩거의 고양이는 양자역학의 코펜하겐 해석이 거시세계에 적용될 때 나타나는 역설을 보여주기 위해 에르빈 슈뢰딩거가 제안한 사고 실험으로, 관측 전까지 고양이가 살아있는 상태와 죽어있는 상태의 중첩으로 존재한다는 양자역학의 해석을 비판하고 다양한 양자역학 해석을 비교하는 데 기여하며 과학철학 및 대중문화에도 영향을 미쳤다.
| 투표의 역설 | |
|---|---|
| 개요 | |
| 유형 | 정치학, 사회 선택 이론 |
| 문제 | 다수결 투표의 비일관성, 순환적 선호 |
| 관련 개념 | 애로우의 불가능성 정리 깁바드-새터스웨이트 정리 합리적 선택 이론 투표의 역설 전략적 투표 |
| 설명 | |
| 정의 | 콩도르세 패자가 존재하지 않는 상황. 즉, 다수결 원칙에 따라 모든 다른 후보를 이기는 후보가 없을 때 발생함. |
| 주요 내용 | 개인의 선호가 이행적이라 할지라도, 집단적 선호는 비이행적일 수 있음을 보여줌. |
| 예시 | 세 명의 유권자와 세 명의 후보 (A, B, C)가 있을 때, A>B, B>C, C>A 와 같은 순환적 선호가 발생할 수 있음. |
| 영향 | |
| 사회 선택 이론 | 사회적 의사 결정 과정의 복잡성을 보여주며, 완벽한 투표 시스템을 설계하는 것이 어려움을 시사함. |
| 정치 | 정치적 불안정, 전략적 투표, 과두제의 가능성 등을 야기할 수 있음. |
| 극복 방안 | |
| 제안된 해결책 | 보르다 계수법 단기 이월식 투표 슈와르츠 집합 콩도르세 기준을 충족하는 다양한 방법들 |
| 한계 | 모든 해결책이 완벽하지 않으며, 각각의 단점과 한계가 존재함. |
2. 역사
콩도르세의 역설은 13세기 카탈루냐의 철학자이자 신학자인 라몬 률이 교회 통치에 대한 연구를 하던 중 처음 발견했지만, 그의 연구는 21세기까지 분실되었다.[1][2][3] 18세기 말, 수학자이자 정치 철학자인 콩도르세 후작이 이 역설을 재발견했다.
콩도르세의 역설은 13세기 카탈루냐의 철학자이자 신학자인 라몬 률이 교회 통치에 대한 연구를 하던 중 처음 발견했지만, 그의 연구는 21세기까지 분실되었다. 18세기 말, 수학자이자 정치 철학자인 콩도르세 후작이 이 역설을 재발견했다.[1]
콩도르세의 발견은 애로우의 불가능성 정리의 핵심 결과를 확인했다는 것을 의미한다. 비록 애로우가 요구하는 조건보다 더 강력한 조건 하에서이긴 하지만, 콩도르세 사이클은 순위 투표 시스템이 다수결을 존중해야 하는 상황을 만들고, 이는 반드시 스포일러 효과를 갖게 된다.
3. 예시
콩도르세의 발견은 애로우의 불가능성 정리의 핵심 결과를 확인했다는 것을 의미한다. 비록 애로우가 요구하는 조건보다 더 강력한 조건에서이긴 하지만, 콩도르세 사이클은 순위 투표 시스템이 다수결을 존중해야 하는 상황을 만들고, 이는 반드시 스포일러 효과를 갖게 된다.
선인장 카운티의 유권자들은 농민당의 현직 카운티 행정관 '''알렉스'''를 태양광 패널당의 경쟁자 '''베아트리체'''보다 약 2대 1의 비율로 선호한다. 올해 세 번째 후보인 '''찰리'''가 무소속으로 출마했다. 찰리는 부유하고 직설적인 사업가로, 유권자들은 그에 대해 양극화된 견해를 가지고 있다. 유권자들은 다음과 같이 세 그룹으로 나뉜다.
다수의 유권자는 알렉스를 베아트리체보다 선호하고(A > B), 베아트리체를 찰리보다 선호하며(B > C), 찰리를 알렉스보다 선호한다(C > A). 이 세 가지 선호를 결합하면 A > B > C > A, 즉 콩도르세 순환이 발생한다.
3. 1. 기본 예시
세 명의 후보 A, B, C와 세 명의 유권자가 있다고 가정한다.
| 유권자 | 첫 번째 선호 | 두 번째 선호 | 세 번째 선호 |
|---|---|---|---|
| 유권자 1 | A | B | C |
| 유권자 2 | B | C | A |
| 유권자 3 | C | A | B |
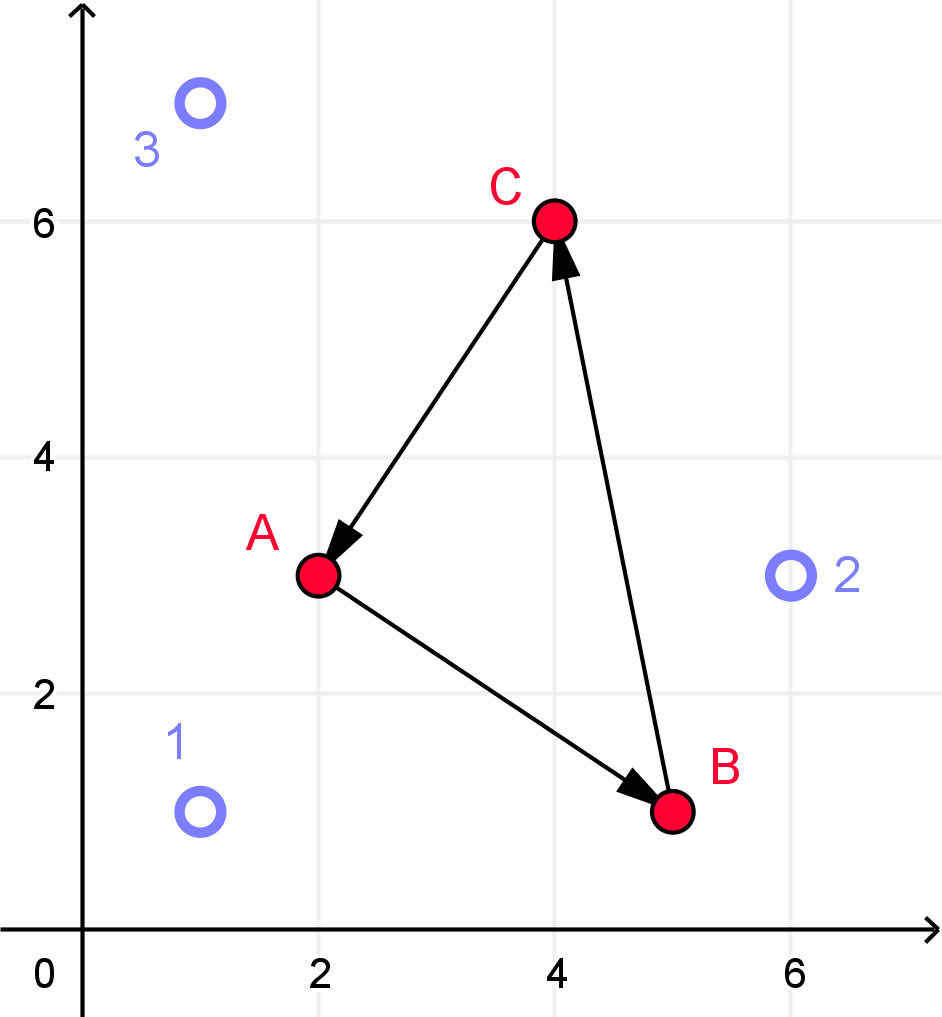
C가 당선자로 선택된다면, 유권자 1과 2는 C보다 B를 선호하고, 유권자 3만이 B보다 C를 선호하므로, B가 대신 당선되어야 한다고 주장할 수 있다. 그러나 같은 논리로 A는 B보다, C는 A보다 선호된다 (각각 두 명 대 한 명). 따라서 사회의 선호도는 순환적인 모습을 보인다. A는 B보다, B는 C보다, C는 A보다 선호된다.
결과적으로 다수결의 원칙에 따르려는 모든 시도는 논리적인 모순으로 이어진다. 어떤 대안을 선택하든, 대부분의 유권자가 선호하는 또 다른 대안을 찾을 수 있다.
선택지가 A, B, C 세 개이고, 투표자가 갑, 을, 병 세 명이며, 세 명의 선호 순서가 아래와 같다고 가정한다.
| 투표자 | 첫 번째 희망 | 두 번째 희망 | 세 번째 희망 |
|---|---|---|---|
| 갑 | A | B | C |
| 을 | B | C | A |
| 병 | C | A | B |
먼저 다수결을 하면 각 투표자가 A, B, C에 각각 투표하기 때문에 답이 나오지 않는다. 그래서 각 선택지를 개별적으로 분석한다.
먼저 A와 C를 비교한다. C보다 A를 선호하는 사람은 갑뿐인데, A보다 C를 선호하는 사람은 을, 병 두 명이다. 따라서 A보다 C가 투표자 집단으로서 선호 순서가 높고, A는 선택되지 않는다. 다음으로 C와 B를 비교하면, C는 B보다 선호 순서가 낮다. 마찬가지로 B는 A보다 낮다. A는 C보다 낮으므로, 결국 끝없는 "A보다 C가 좋고, C보다 B가 좋고, B보다 A가 좋고, A보다 C가..."가 반복되어 답을 낼 수 없다.
이러한 모순을 "정치적"으로 해결하는 방법으로, 의도적으로 먼저 A와 B의 선택 투표를 실시하여 B를 제거한 후 A와 C를 비교하여 최종적으로 C를 선택하는 방법이 있다. 즉, 투표 절차의 결정권을 쥐고 있는 경우에는 결과를 조작할 수 있다.
3. 2. 실제 시나리오 (미국 미니애폴리스 시의회 선거)
2021년 미니애폴리스 시의회 2구 선거에서는 녹색당 후보 캠 고든, 미네소타 민주-농민-노동당 후보 유스라 아랍, 무소속 민주적 사회주의 후보 로빈 원슬리 간의 좁은 순환적 무승부가 발생했다.[16] 유권자들의 선호도는 비전이적이었는데, 아랍은 고든보다 선호되었고, 고든은 원슬리보다, 원슬리는 아랍보다 선호되어 명확한 승자가 없는 순환 패턴을 만들었다. 이 선거는 하향 단조성 역설뿐만 아니라 심슨의 역설과 유사한 역설도 보였다. 이 사례는 2004년부터 2022년까지 미국에서 치러진 189개의 순위 투표 데이터베이스에서 발견된 유일한 콩도르세 순환이었다.[16]4. 발생 가능성
콩도르세 역설이 발생할 확률은 유권자 행동 모델에 따라 달라진다.
- 무차별 문화 모델 (Impartial culture model): 유권자 선호가 후보자들 사이에 균등하게 분포된다고 가정한다. 이 경우, 세 후보자에 대한 콩도르세 역설 발생 확률은 약 8.77%이다.[8][9] 후보자가 늘어날수록 확률은 더 높아진다.[11]
- 집단 응집 모델 (Group coherence models): 무차별 익명 문화(IAC), 균일 문화(UC), 최대 문화 조건(MC) 등이 여기에 해당하며, 유권자 선호가 특정 집단에 따라 쏠리는 경향을 반영한다. 이 경우 역설 발생 확률은 무차별 문화 모델보다 낮다.[9]
- 공간 모델 (Spatial model): 유권자와 후보자를 다차원 공간에 배치하여 선호를 나타낸다. 실제 순위 투표 선거 데이터에 가장 잘 부합하는 모델로 알려져 있으며,[12] 유권자 수가 증가함에 따라 사이클 발생 확률이 0으로 감소한다.[12]
경험적 연구에 따르면, 실제 선거에서 콩도르세 역설이 발생하는 경우는 드물다.[5][14] 총 265개의 실제 선거를 다룬 연구에서는 9.4%의 발생 확률을 보였지만,[6] 이는 역설 사례가 더 많이 보고되었을 가능성을 고려하면 높은 추정치일 수 있다.[5] 선거 개혁 협회의 분석에서는 0.7%, 미국 전국 선거 연구 데이터 분석에서는 0.4%의 발생 확률을 보였다.[12]
5. 시사점 및 영향
콩도르세 역설은 다수결 투표 방식이 가진 문제점을 보여준다. 의회에서 투표 순서에 따라 최종 결과가 달라질 수 있으며, 이는 의도적인 결과 조작으로 이어질 수 있다. 예를 들어, 인기 있는 법안에 '독소 조항' 수정안을 붙여 법안 통과를 막는 경우가 있다.[1] 이러한 문제는 대한민국 정치에서도 나타날 수 있는데, 다당제 환경에서 연립 정부를 구성하거나 정당 간 정책 합의를 이루는 데 어려움을 겪을 수 있다.
콩도르세 역설은 '무관한 대안의 독립성' 공리를 위반한다. 즉, 관련 없는 후보의 존재가 선거 결과에 영향을 미치는 '스포일러 효과'를 낳을 수 있다.[17] 예를 들어, 세 후보 A, B, C가 있고, 유권자들의 선호도가 다음과 같다고 가정해 보자.
| 투표자 | 첫 번째 선호 | 두 번째 선호 | 세 번째 선호 |
|---|---|---|---|
| 갑 | A | B | C |
| 을 | B | C | A |
| 병 | C | A | B |
이 경우, 다수결 투표로는 결론을 내릴 수 없다. A와 C를 비교하면 C가, C와 B를 비교하면 B가, B와 A를 비교하면 A가 선호되어 순환이 발생하기 때문이다.
이러한 상황에서 투표 순서를 조작하면 결과를 바꿀 수 있다. 예를 들어, 먼저 A와 B를 투표하여 B를 탈락시킨 후 A와 C를 비교하면 C가 최종 선택될 수 있다.
콩도르세 투표 방법은 모든 후보 간 일대일 대결을 통해 가장 선호되는 후보(콩도르세 승자)를 찾는다.[1] 하지만 콩도르세 역설이 발생하면 콩도르세 승자가 존재하지 않아 당락을 결정할 수 없는 경우가 생긴다.
6. 콩도르세 투표 방법
콩도르세 방법은 모든 후보 간 일대일 비교를 통해 가장 선호되는 후보를 찾는 투표 방식이다. 콩도르세 승자는 다른 모든 후보와의 일대일 대결에서 승리하는 후보를 의미한다. 반대로, 콩도르세 패자는 다른 모든 후보와의 일대일 대결에서 패배하는 후보를 의미한다.[17]
콩도르세 방법은 콩도르세 승자/패자 기준을 만족하지만, 투표의 역설이 발생하여 당락을 결정하지 못하는 경우가 있을 수 있다. 투표의 역설은 순환하는 사회적 선호 때문에 발생하며, 콩도르세 승자가 없는 상황을 초래한다. 즉, 다른 모든 후보를 상대로 일대일 선거에서 이기는 후보가 없는 것이다. 이러한 순환 모호성을 해결하기 위해 다양한 콩도르세 방법 변형이 존재한다. 예를 들어, 스미스 집합은 최소 후보 그룹으로, 이 그룹의 각 후보는 그룹 외부의 각 후보를 상대로 일대일 선거에서 승리할 수 있다. 스미스 효율적인 콩도르세 방법은 콩도르세 승자가 없을 때 항상 스미스 집합에서 누군가를 선출한다.[17]
예를 들어, 선택지가 A, B, C 세 개이고, 투표자가 갑, 을, 병 세 명이며, 선호 순서가 다음과 같다고 가정해 보자.
| 투표자 | 첫 번째 희망 | 두 번째 희망 | 세 번째 희망 |
|---|---|---|---|
| 갑 | A | B | C |
| 을 | B | C | A |
| 병 | C | A | B |
다수결을 적용하면 각 투표자가 A, B, C에 각각 투표하여 답이 나오지 않는다. 각 선택지를 개별적으로 분석하면 다음과 같다.
- A와 C 비교: C보다 A를 선호하는 사람은 갑뿐이고, A보다 C를 선호하는 사람은 을, 병 두 명이다. 따라서 A는 C에게 패배한다.
- C와 B 비교: C는 B보다 선호 순서가 낮다.
- B와 A 비교: B는 A보다 선호 순서가 낮다.
결과적으로, "A보다 C가 좋고, C보다 B가 좋고, B보다 A가 좋고, A보다 C가..."와 같은 끝없는 순환이 발생하여 답을 낼 수 없다. 이러한 경우, 투표 절차를 조작하여 결과를 바꿀 수 있다. 예를 들어, 의도적으로 A와 B의 선택 투표를 먼저 실시하여 B를 제거한 후 A와 C를 비교하여 최종적으로 C를 선택하는 방식이 가능하다.
7. 대한민국 정치에 대한 함의
(이전 출력이 없으므로, 수정할 내용이 없습니다. 원본 소스와 함께 이전 출력을 제공해주시면 수정 작업을 진행할 수 있습니다.)
참조
[1]
서적
Essai sur l'application de l'analyse à la probabilité des décisions rendues à la pluralité des voix
http://gallica.bnf.f[...]
2008-03-10
[2]
서적
The political theory of Condorcet
University of Oxford, Faculty of Social Studies
1989-01-01
[3]
논문
Condorcet's paradox and the likelihood of its occurrence: different perspectives on balanced preferences*
[4]
논문
The impartial culture maximizes the probability of majority cycles
2003-12-01
[5]
서적
Voting paradoxes and group coherence : the condorcet efficiency of voting rules
Springer
2011
[6]
논문
On the empirical relevance of Condorcet's paradox
2014
[7]
논문
Some mathematical remarks on the paradox of voting
1971
[8]
논문
Les théories de l'intérêt général et le problème logique de l'agrégation
2012
[9]
논문
Condorcet's paradox and the likelihood of its occurrence: different perspectives on balanced preferences*
https://doi.org/10.1[...]
2002-03-01
[10]
논문
Condorcet's paradox and the Condorcet efficiency of voting rules
https://www.research[...]
1997
[11]
논문
A Comparison of Efficiency of Multicandidate Electoral Systems
https://www.jstor.or[...]
1984
[12]
간행물
Modeling the Outcomes of Vote-Casting in Actual Elections
http://link.springer[...]
Springer Berlin Heidelberg
2021-11-12
[13]
논문
Empirical social choice: An introduction
2014
[14]
논문
An empirical example of the Condorcet paradox of voting in a large electorate
2001
[15]
conference
The Frequency of Condorcet Winners in Real Non-Political Elections
https://www.cs.corne[...]
2024-03
[16]
arXiv
An Examination of Ranked Choice Voting in the United States, 2004-2022
2023-01-28
[17]
서적
Math in society
CreateSpace Independent Publishing Platform
[18]
논문
Condorcet's paradox and the likelihood of its occurrence: different perspectives on balanced preferences*
https://doi.org/10.1[...]
2002-03-01
[19]
논문
On the empirical relevance of Condorcet's paradox
https://doi.org/10.1[...]
2014-03-01
[20]
뉴스
다수결 투표에 숨어 있는 함정
https://www.sciencet[...]
사이언스타임즈
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com