트로미노
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
트로미노는 세 개의 정사각형으로 구성된 도형으로, 회전과 반사를 고려하지 않는 자유 트로미노는 I형과 L형 두 가지가 있다. 트로미노는 렙타일의 일종으로, L형 트로미노는 재귀적으로 분할하여 비주기적 타일링을 만들 수 있으며, 솔로몬 W. 골롬은 이를 바탕으로 2n × 2n 체스판에서 임의의 정사각형을 제거하면 L-트로미노로 덮을 수 있다는 골롬의 트로미노 정리를 제시했다. 트로미노를 이용한 직사각형 만들기 문제와 체스판 채우기 문제 등이 있으며, I형 트로미노를 사용할 경우 빈칸의 위치가 제한된다.
더 읽어볼만한 페이지
| 트로미노 | |
|---|---|
| 기본 정보 | |
| 종류 | 폴리오미노 |
| 구성 | 정사각형 3개 |
| 종류별 명칭 | |
| I형 | 스트레이트 트로미노, 아이 트로미노 |
| L형 | 엘 트로미노 |
| 대칭성 | |
| I형 | 대칭 |
| L형 | 비대칭 |
| 활용 | |
| 관련 게임 | 트라이오미노스 |
2. 종류
트로미노는 연결된 세 개의 정사각형으로 구성된 도형이다. 회전과 반사를 서로 다른 도형으로 간주하지 않는 자유 트로미노는 "I"와 "L"(또는 "V") 두 가지가 있다.[2][3] 두 자유 트로미노 모두 반사 대칭을 가지므로, 단면 트로미노 또한 I형과 L형 두 가지이다. 회전을 서로 다른 것으로 간주하는 고정 트로미노는 I형 2가지, L형 4가지로 총 6가지이다. I형은 180도 회전 대칭이지만, L형은 회전 대칭이 아니다.[7]
두 가지 자유 트로미노는 I형과 L형("V"라고도 불린다)이 있으며, 모두 반사 대칭을 갖는다.[2][3] 따라서 유일한 두 개의 ''일면'' 트로미노(반사를 서로 다른 것으로 간주하는 트로미노)이기도 하다. I형 트로미노는 180도 회전 대칭이지만, L형 트로미노는 회전 대칭이 아니다.[7]
트로미노는 렙타일(rep-tile)이다.[4] 즉, n > 1인 모든 정수 n에 대해 n²개의 더 작은 같은 모양 트로미노로 분할될 수 있다.
솔로몬 W. 골롬(Solomon W. Golomb)은 손상된 체스판 문제에서 영감을 받아 골롬의 트로미노 정리를 제시했다.[6] 골롬의 트로미노 정리에 따르면, 2''n'' × 2''n'' 체스판에서 임의의 정사각형 하나를 제거하면, 나머지 보드는 L-트로미노로 완전히 덮을 수 있다.[6] 이는 수학적 귀납법으로 증명할 수 있는데, 보드를 제거된 정사각형을 포함하는 2''n−1'' × 2''n−1'' 크기의 4분의 1 보드와, 나머지 세 개의 4분의 1 보드로 형성된 큰 트로미노로 분할하는 방식으로 증명한다. 트로미노는 재귀적으로 단위 트로미노로 분할될 수 있으며, 하나의 정사각형이 제거된 4분의 1 보드의 분할은 귀납적 가설에 의해 가능하다.[6]
폴리오미노에서 일반적인 "세트를 모두 한 번씩 사용하여 모양을 만든다"는 문제는 조각 수가 적기 때문에 트로미노의 경우 출제되지 않는다.
3. 대칭성
4. 렙타일과 타일링

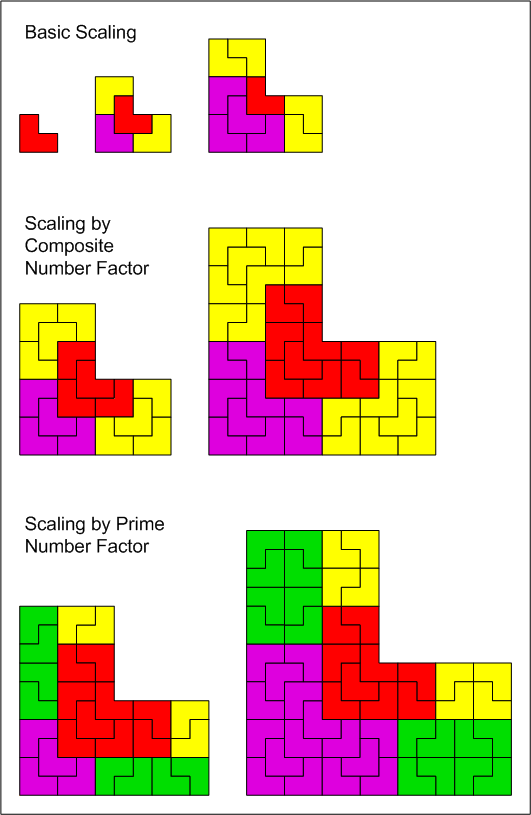
L-트로미노를 재귀적으로 분할하여 평면 타일링을 만들 수 있으며, 이는 많은 경우에 비주기적 타일링이 된다.[5] 이러한 맥락에서, L-트로미노는 "의자"라고 불리며, 이를 4개의 더 작은 L-트로미노로 재귀적으로 분할하여 타일링하는 것을 의자 타일링이라고 한다.[5]
손상된 체스판 문제에서 영감을 얻은 솔로몬 W. 골롬(Solomon W. Golomb)은 이 타일링을 기반으로 골롬의 트로미노 정리가 알려지게 되었다: 2''n'' × 2''n'' 체스판에서 임의의 정사각형을 제거하면, 나머지 보드는 L-트로미노로 완전히 덮을 수 있다. 이를 수학적 귀납법으로 증명하기 위해, 보드를 제거된 정사각형을 포함하는 2''n−1'' × 2''n−1'' 크기의 4분의 1 보드와, 나머지 세 개의 4분의 1 보드로 형성된 큰 트로미노로 분할한다. 트로미노는 재귀적으로 단위 트로미노로 분할될 수 있으며, 하나의 정사각형이 제거된 4분의 1 보드의 분할은 귀납적 가설에 의해 따른다. 이와 대조적으로, 이 크기의 체스판에서 하나의 정사각형이 제거되면, 나머지 정사각형을 I-트로미노로 덮는 것이 항상 가능한 것은 아니다.[6]
L형 트로미노를 합동인 4개의 도형으로 분할하는 문제가 있다. 이 문제에서는 출제 시 형태의 조건은 주어지지 않지만, 한 변이 절반인 L형 트로미노로 분할할 수 있다. 이 4 조각을 마찬가지로 분할함으로써, 4n 조각의 합동인 L형 트로미노로 분할할 수 있다.
5. 골롬의 트로미노 정리
이와 대조적으로, 같은 크기의 체스판에서 하나의 정사각형이 제거되면, 나머지 정사각형을 I-트로미노로 덮는 것이 항상 가능한 것은 아니다.[6] I형 트로미노를 놓는 경우, 빈칸의 위치는 한정되며, 이 빈칸의 위치를 구하는 문제는 헝가리의 수학 경시대회에서 출제된 적이 있다.
6. 트로미노 문제 (일본어판 내용 추가)
==== 직사각형 만들기 ====
단면 유향 트로미노 6종류로 직사각형을 만드는 것은 가능하다.[8] 트로미노 2세트를 사용하여 3×4나 2×6의 직사각형을 만들 수 있다.[8]
한 종류의 조각을 여러 개 사용하여 직사각형을 만드는 문제는 I형의 경우 자명하다. L형도 2조각으로 2×3의 직사각형을 만들 수 있으므로 간단하다. 아시가하라 노부유키는 이 2×3 직사각형의 사용을 금지한 문제를 출제했다.[8]
==== 체스판 채우기 ====
2가지 트로미노는 모두 렙타일이기 때문에 1보다 큰 모든 정수 n에 대하여 n²개의 더 작은 같은 모양으로 채울 수 있다.
같은 종류의 트로미노를 체스판에 놓는 것을 생각해 보자. 체스판은 8×8=64칸이므로, 21개를 놓으면 1칸이 남는다.
L형 트로미노를 놓는 경우, 빈칸은 어디에 있어도 문제가 없다. 실제로 2n×2n 의 바둑판에서 임의의 1칸을 제외한 도형은 L형 트로미노로 채울 수 있다는 것을 귀납법으로 증명할 수 있다.
I형 트로미노를 사용하는 경우에는 빈칸의 위치가 제한된다. 이 빈칸의 위치를 구하는 문제는 헝가리의 수학 경시대회에서 출제된 적이 있다.
6. 1. 직사각형 만들기
단면 유향 트로미노 6종류로 직사각형을 만드는 것은 가능하다.[8] 트로미노 2세트를 사용하여 3×4나 2×6의 직사각형을 만들 수 있다.[8]
한 종류의 조각을 여러 개 사용하여 직사각형을 만드는 문제는 I형의 경우 자명하다. L형도 2조각으로 2×3의 직사각형을 만들 수 있으므로 간단하다. 아시가하라 노부유키는 이 2×3 직사각형의 사용을 금지한 문제를 출제했다.[8]
6. 2. 체스판 채우기
2가지 트로미노는 모두 렙타일이기 때문에 1보다 큰 모든 정수 n에 대하여 n²개의 더 작은 같은 모양으로 채울 수 있다.
같은 종류의 트로미노를 체스판에 놓는 것을 생각해 보자. 체스판은 8×8=64칸이므로, 21개를 놓으면 1칸이 남는다.
L형 트로미노를 놓는 경우, 빈칸은 어디에 있어도 문제가 없다. 실제로 2n×2n 의 바둑판에서 임의의 1칸을 제외한 도형은 L형 트로미노로 채울 수 있다는 것을 귀납법으로 증명할 수 있다.
I형 트로미노를 사용하는 경우에는 빈칸의 위치가 제한된다. 이 빈칸의 위치를 구하는 문제는 헝가리의 수학 경시대회에서 출제된 적이 있다.
7. 관련 문서
- 도미노
- 테트로미노
참조
[1]
서적
Polyominoes
Princeton University Press
[2]
MathWorld
Triomino
[3]
논문
Counting polyominoes: yet another attack
[4]
간행물
MASS selecta
American Mathematical Society
[5]
논문
On the table and the chair
[6]
논문
Checker boards and polyominoes
[7]
MathWorld
Triomino
[8]
서적
パズルの宣教師
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com