펠릭스 하우스도르프

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 생애
3. 학문적 업적
4. 저술 활동 (파울 몽그레)
5. 유산 및 평가
참조

1. 개요

펠릭스 하우스도르프는 20세기 초 독일의 수학자이자 철학자이며, 위상수학, 집합론, 측도론, 함수해석학 등 다양한 분야에 걸쳐 중요한 업적을 남겼다. 그는 '파울 몽그레'라는 필명으로 철학 및 문학 작품을 발표하기도 했다. 하우스도르프는 라이프치히 대학교에서 교수로 재직하며 집합론의 기초를 다졌고, '집합론 기초'를 저술하여 집합론의 표준적인 저서로 만들었다. 또한 하우스도르프 공간, 하우스도르프 차원 등의 개념을 도입하여 위상수학 발전에 기여했다. 나치 정권의 반유대주의 정책으로 인해 강제 퇴직당한 후, 1942년 아내, 처제와 함께 자살했다. 그의 업적을 기려 다양한 수학적 개념과 연구 기관의 명칭에 그의 이름이 사용되고 있다.

더 읽어볼만한 페이지

1942년 자살 - 슈테판 츠바이크
슈테판 츠바이크는 20세기 초 오스트리아 출신의 소설가, 극작가, 전기 작가로, 인간 심리와 역사적 사실에 대한 묘사로 유명하며, 나치 정권의 박해를 피해 망명 생활 중 아내와 함께 자살했고, 《조제프 푸셰》, 《마리 앙투아네트》, 《어제의 세계》 등의 작품을 남겼다.
동반 자살 - 하인리히 폰 클라이스트
하인리히 폰 클라이스트는 18세기 말에서 19세기 초 활동한 독일의 극작가, 소설가, 시인으로, 격정적이고 비극적인 분위기의 작품을 남겼으며 사회적 고립 속에서 자살로 생을 마감했지만 20세기 초에 재평가되어 천재적인 극작가로 인정받았다.
동반 자살 - 노기 마레스케
노기 마레스케는 메이지 시대와 다이쇼 시대에 활약한 일본 제국 육군 대장으로, 청일 전쟁과 러일 전쟁에 참전하여 공을 세웠으나 막대한 인명 피해에 대한 비판도 존재하며, 메이지 천황 서거 후 아내와 함께 자결하여 충절의 상징으로 여겨지지만 군사적 능력과 자결에 대한 평가는 엇갈리는 인물이다.
브로츠와프 출신 - 크리스티안 볼프
크리스티안 볼프는 라이프니츠 철학을 계승 발전시켜 칸트 이전 독일 철학계를 지배한 독일의 철학자, 법학자, 수학자로, 다양한 분야에서 저술을 남기고 독일어 철학 용어 확립에 기여하여 계몽주의 사상 발전에 영향을 미쳤다.
브로츠와프 출신 - 프리드리히 베르기우스
프리드리히 베르기우스는 독일의 화학자로, 고압 및 고온 화학 공정 기술 개발, 특히 베르기우스법을 통한 합성 연료 생산과 목재 가수분해를 통한 산업용 설탕 생산 기술 개발에 기여하여 1931년 노벨 화학상을 수상했지만, 후기 연구의 어려움과 전쟁 후 상황으로 아르헨티나에서 생을 마감했다.

펠릭스 하우스도르프 - [인물]에 관한 문서
기본 정보
이름	펠릭스 하우스도르프
출생일	1868년 11월 8일
출생지	브로츠와프, 프로이센 왕국 (현재 폴란드 브로츠와프)
사망일	1942년 1월 26일
사망지	본, 독일
국적	독일
학문 분야
분야	수학
모교	라이프치히 대학교
지도 교수	하인리히 브룬스 아돌프 마이어
박사 학위 논문	천문 굴절 이론에 관하여 (Zur Theorie der astronomischen Strahlenbrechung)
박사 학위 년도	1891년
제자	카를 베겔 프란츠 할렌바흐 (Franz Hallenbach) 구스타프 슈타인바흐 (Gustav Steinbach)
알려진 업적	η 집합 백-앤-포스 방법 (Back-and-forth method) 베이커-캠벨-하우스도르프 공식 (Baker–Campbell–Hausdorff formula) 하우스도르프 완비화 (Hausdorff completion) 하우스도르프 차원 (Hausdorff dimension) 하우스도르프 거리 (Hausdorff distance) 하우스도르프 갭 (Hausdorff gap) 하우스도르프 최대 원리 (Hausdorff maximal principle) 하우스도르프 측도 (Hausdorff measure) 하우스도르프 역설 (Hausdorff paradox) 하우스도르프 공간 (Hausdorff space) 하우스도르프 모멘트 문제 (Hausdorff moment problem) 하우스도르프-영 부등식 (Hausdorff–Young inequality)
근무 기관
근무 기관	본 대학교 그라이프스발트 대학교 라이프치히 대학교
개인 정보
배우자	샬로테 하우스도르프 (Charlotte Hausdorff, 1873-1942)
기타 정보
로마자 표기	Pellikseu Hauseudo Repeu

2. 생애

펠릭스 하우스도르프는 프로이센령 브레슬라우(현재 폴란드 브로츠와프)의 유대인 가정에서 태어나 라이프치히에서 성장했다. 어린 시절 음악에 재능을 보였으나 라이프치히와 프라이부르크에서 대학을 다니며 천문학을 공부했다. 1891년 박사 학위를 취득한 후 군 복무와 계산수 경력을 거쳐 라이프치히 대학교에서 교수 자격을 얻었다. 1899년 샤를로테 슈미트와 결혼하여 딸 하나를 두었다.

2. 1. 유년 시절과 교육

펠릭스 하우스도르프는 1868년 11월 8일, 당시 프로이센령이었던 브레슬라우(현재 폴란드 브로츠와프)에서 유대인 상인 루이스 하우스도르프(1843–1896)의 아들로 태어났다.^[1] 그의 아버지는 교육받은 사람으로, 14세에 모레누가 되었으며 탈무드 율법과 관련된 여러 논문을 저술하기도 했다. 어머니 헤드비히(1848–1902)는 유대인 티에츠 가문 출신으로, 이 가문에서는 유명 백화점 체인 "헤르만 티에츠"(나치 시대에 헤르티로 변경됨)의 창립자 헤르만 티에츠가 나왔다.^[2] 1870년 가을, 가족은 라이프치히로 이주했으며, 하우스도르프는 그곳에서 성장했다.^[1] 그의 가족은 유대교 신앙 배경을 가졌으나, 하우스도르프 자신은 불가지론적 성향을 보였다.^[3]

1878년부터 1887년까지 하우스도르프는 인문주의 교육으로 명성이 높았던 라이프치히의 니콜라이 학교에 다녔다.^[2] 그는 뛰어난 학생으로 여러 해 동안 반장을 맡았고, 학교 행사에서 직접 쓴 라틴어 또는 독일어 시를 자주 낭송했다.^[2] 그는 음악에도 뛰어난 재능을 보였으며 작곡가를 꿈꾸기도 했다. 1926년부터 1932년까지 하우스도르프의 집을 자주 방문했던 마그다 디에르케스만은 1967년에 "그의 다재다능한 음악적 재능은 너무나 뛰어났기에 아버지의 강요가 아니었다면 음악을 공부하여 작곡가가 되려는 계획을 포기하지 않았을 것"이라고 회고했다.^[4] 하지만 아버지의 강한 권유로 그는 자연 과학을 공부하기로 결정했고, 1887년 졸업 시에는 최고 점수를 받은 유일한 학생이었다.^[2]

1887년부터 1891년까지 하우스도르프는 주로 고향인 라이프치히에서 수학과 천문학을 공부했으며, 프라이부르크(1888년 여름 학기)와 베를린(1888/1889년 겨울 학기)에서도 각각 한 학기씩 수학했다.^[2]^[1] 그는 수학과 천문학 외에도 물리학, 화학, 지리학 강의를 들었으며, 철학, 철학사, 언어학, 문학, 사회 과학 등 다양한 분야에 걸쳐 폭넓은 관심을 보였다.^[2] 라이프치히에서는 음악학자 오스카 파울에게 음악사 강의를 듣기도 했으며, 리하르트 바그너의 음악을 특히 좋아했다. 음악에 대한 그의 열정은 평생 지속되어, 훗날 자택에서 직접 피아노를 연주하며 음악회를 열기도 했다.^[2]

학업 후반기에 하우스도르프는 라이프치히 대학교 천문학 교수이자 천문대장이었던 하인리히 브룬스(1848–1919)의 지도를 받았다.^[2] 1891년, 그는 브룬스의 지도 아래 "대기 중 빛의 천문학적 굴절 이론"에 대한 연구로 박사 학위를 취득했다.^[2]^[1] 이후 같은 주제로 두 편의 논문을 더 발표했고, 1895년에는 "대기 중 빛의 흡수"에 관한 논문으로 교수 자격(Habilitation)을 얻었다.^[2] 박사 학위와 교수 자격 취득 사이의 기간에는 1년간의 의무 군 복무를 마치고 라이프치히 천문대에서 2년간 계산원으로 일했다.^[2]^[3]

하우스도르프의 초기 천문학 연구는 수학적으로는 정교했지만, 과학계에 큰 영향을 미치지는 못했다.^[2]^[3] 스승 브룬스의 연구 방향이 실제 관측의 정확도 문제로 한계에 부딪혔고, 기상 관측 기술의 발달로 대기 데이터의 직접 측정이 가능해지면서 그의 연구 방식의 필요성이 줄어들었기 때문이다.^[2]

2. 2. 라이프치히에서의 교수 생활 (1895-1910)

1895년 라이프치히 대학교에서 교수 자격을 취득한 후, 하우스도르프는 같은 대학의 강사가 되어 다양한 수학 분야에서 폭넓은 강의를 시작했다. 그는 수학 강의와 연구 외에도 문학 및 철학 활동에 깊은 관심을 보였다. 헤르만 콘라디, 리하르트 데멜, 오토 에리히 하트레벤, 구스타프 키르스틴, 막스 클링거, 막스 레거, 프랑크 베데킨트와 같은 당대의 저명한 작가, 예술가, 출판업자들과 활발히 교류했다.

특히 1897년부터 1904년까지는 그의 문학적, 철학적 창작 활동이 가장 왕성했던 시기였다. 이 기간 동안 그는 '파울 몽그레'(Paul Mongré^de)라는 필명으로 시집, 희곡, 인식론 서적, 격언집 등 총 18편의 저작물을 출판했다. 이는 그가 필명으로 발표한 총 22개 작품 중 대부분에 해당한다. 제1차 세계 대전 이후의 사전에서는 그를 저명한 수학자이자 작가로 기록하기도 했다.

1899년, 하우스도르프는 유대인 의사 지기스문트 골트슈미트의 딸인 샤를로테 골트슈미트와 결혼했다. 샤를로테의 계모는 유명한 여성 참정권 운동가이자 유치원 교사인 앙리에테 골트슈미트였다. 1900년에는 외동딸 레노어(노라)가 태어났다.

라이프치히에서 활동하는 동안 하우스도르프의 수학적 관심사도 변화했다. 초기에는 조건부 확률, 보험수학 응용 등에 관한 논문을 발표했지만, 점차 집합론과 위상수학으로 연구 방향을 옮겨갔고, 이는 그의 평생 연구 주제가 되었다. 그는 학생들에게 집합론의 기초를 가르치기 시작했으며, 이는 훗날 방대한 체계로 발전하게 될 연구의 시작이었다.

1901년 라이프치히 대학교의 교수로 정식 임용되었으나, 당시 만연했던 노골적인 반유대주의 분위기 때문에 학문적 성취에도 불구하고 주류 학계에서 경력을 쌓는 데 어려움을 겪었다. 그는 이러한 환경 속에서도 문학 및 예술계와의 교류를 계속 이어갔다. 결국 하우스도르프는 라이프치히에서의 생활이 만족스럽지 못하고, 과학 분야에서의 미래 경력을 위해 새로운 환경이 필요하다고 판단하여 1910년 본 대학교의 교수직을 수락하며 라이프치히를 떠났다.

2. 3. 본 대학교 및 그라이프스발트 대학교 교수 생활 (1910-1921)

1910년 여름 학기에 하우스도르프는 본 대학교 교수로 임명되었다. 그는 본에서 집합론에 대한 강의를 시작했으며, 1912년 여름 학기에는 이 강의 내용을 크게 수정하고 확장했다.

1912년 여름, 하우스도르프는 그의 대표적인 저서인 ''집합론의 기초''(Grundzüge der Mengenlehre^de) 집필에 착수했다. 이 책은 그가 1913년 여름 학기에 정교수로 임명된 그라이프스발트 대학교에서 완성되었고, 1914년 4월에 출판되었다.

그라이프스발트 대학교는 당시 프로이센의 대학 중 가장 작은 규모였으며, 수학 연구소 역시 마찬가지였다. 특히 1916년 여름 학기와 1916/17년 겨울 학기에는 하우스도르프가 그 대학의 유일한 수학자였기 때문에, 주로 기본적인 수학 강좌를 가르치는 데 집중해야 했다. 이러한 환경은 그의 연구 활동에 제약을 주었을 수 있다.

2. 4. 본 대학교 복귀와 나치 치하의 핍박 (1921-1942)

나치 정권이 권력을 장악한 후, 반유대주의는 국가 정책의 핵심이 되었다. 1933년 제정된 "전문 공무원 복원법"은 유대인 공무원을 추방하기 위한 법이었으나, 하우스도르프는 1914년 이전에 임용된 공무원이었기에 처음에는 큰 영향을 받지 않을 것으로 여겼다. 그러나 그는 완전한 면제 대상이 아니었고, 실제로 그의 강의 중 하나가 나치 학생 간부들에 의해 방해받는 일도 발생했다. 1934년에서 1935년으로 넘어가는 겨울 학기에는 본 대학교에서 국가사회주의 독일 학생 동맹(NSDStB)이 "인종과 민족"을 주제로 행사를 열었다. 하우스도르프는 1934년 11월 20일, 해당 학기의 미적분학 III 강좌를 갑자기 취소했는데, 이는 그의 오랜 교수 경력 동안 처음 있는 일이었기에 이러한 주제 선정과 무관하지 않았을 것으로 추정된다.

결국 여러 차례의 압박 끝에 하우스도르프는 1935년 3월 31일부로 강제로 명예 교수직을 받아들여야 했다. 독일 고등 교육계에 40년간 기여한 그의 업적에 대한 어떤 감사나 예우도 없었다.

그의 사후 저작물은 이처럼 어려운 시기에도 하우스도르프가 수학 연구를 멈추지 않았으며, 당시 학계의 최신 동향에도 꾸준히 관심을 가졌음을 보여준다. 그는 자신의 주요 저서인 《집합론》의 개정판 작업 외에도, 위상수학 및 기술 집합론 분야에서 7편의 논문을 완성했다. 이 논문들은 폴란드의 학술지인 ''Studia Mathematica''와 ''Fundamenta Mathematicae''에 발표되었다. 이 시기 동안 하우스도르프는 그의 오랜 친구인 에리히 베셀-하겐의 도움을 받았다. 베셀-하겐은 하우스도르프가 더 이상 접근할 수 없게 된 대학 도서관에서 필요한 책과 학술지를 구해다 주었다.

1938년 수정의 밤 사건 이후 유대인에 대한 박해와 굴욕은 더욱 심해졌으며, 이는 하우스도르프와 그의 가족에게도 예외는 아니었다. 당시 상황은 베셀-하겐이 남긴 편지 등 여러 자료를 통해 알려져 있다.^[6]

1939년, 하우스도르프는 수학자 리하르트 쿠랑을 통해 미국으로 이주하기 위한 연구 지원금을 신청했지만, 이는 거절되었다.

1941년 중반부터 본에 거주하던 유대인들은 엔데니히에 위치한, 기존 수녀들이 쫓겨난 '영원 경배 수녀원'으로 강제 이주되기 시작했다. 이후에는 동부의 절멸 수용소로 이송되었다. 1942년 1월, 하우스도르프와 그의 아내 샤를로테, 그리고 함께 살던 처제 에디트 파펜하임에게도 엔데니히 수용소로 이주하라는 명령이 내려졌다. 수용소행이 곧 죽음으로 이어질 것임을 직감한 세 사람은 1942년 1월 26일, 베로날 과다 복용으로 함께 목숨을 끊었다.^[7] 그들의 유해는 본의 포펠스도르프 공동묘지에 안장되었다.

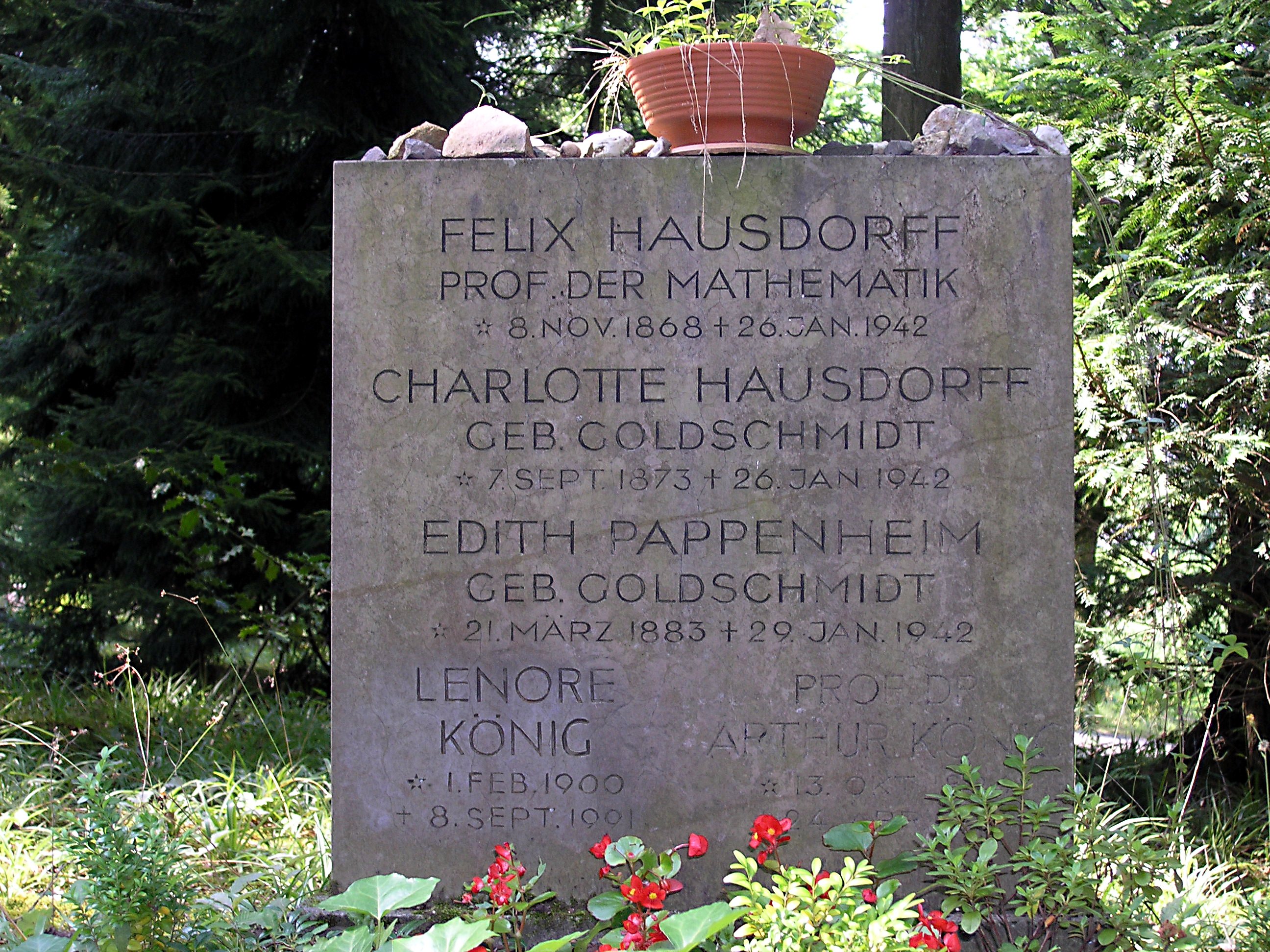
하우스도르프는 죽음을 앞두고 자신의 손으로 쓴 방대한 양의 연구 자료를 이집트학자이자 목사였던 한스 보네에게 맡겼다. 보네는 이후 폭격으로 자신의 집이 파괴되는 와중에도 이 자료들을 최대한 보존하려 애썼다.

엔데니히 임시 수용소에 대해 일부 유대인들은 희망적인 환상을 가졌을지도 모르지만, 하우스도르프는 현실을 냉철하게 인식하고 있었다. 그의 작별 편지는 변호사이자 역시 유대인이었던 한스 볼슈타인에게 보내졌는데, 이 편지는 후에 베셀-하겐의 유품 속에서 E. 노이엔슈반더에 의해 발견되었다.^[8]^[9] 편지의 시작 내용은 다음과 같다.

"친애하는 친구 볼슈타인!

만약 이 글을 받으신다면, 우리(세 명)는 문제를 다른 방식으로 해결했습니다. 당신이 우리에게 계속 설득하려 했던 방식으로요. 이사 문제들을 극복하면 당신이 우리에게 예측했던 안전감은 아직 우리를 피해 가고 있습니다. 반대로, 엔데니히가 끝이 아닐 수도 있습니다!

최근 몇 달 동안 유대인들에게 일어난 일들은 그들이 우리를 더 견딜 수 있는 상황을 볼 수 있도록 내버려두지 않을 것이라는 정당한 두려움을 불러일으킵니다."

친구들에게 감사를 표하고, 매우 침착하게 그의 장례식과 유언에 관한 마지막 소원을 표현한 후, 하우스도르프는 다음과 같이 편지를 맺었다.

"죽음 이후에도 더 많은 노력을 기울이게 해서 죄송하며, 당신이 할 수 있는 모든 것(아마도 많지는 않겠지만)을 하고 있다고 확신합니다. 우리의 배신을 용서하십시오! 우리는 당신과 모든 친구들이 더 나은 시대를 경험하기를 바랍니다.

진심으로 헌신하는

펠릭스 하우스도르프"

안타깝게도 하우스도르프의 마지막 바람은 이루어지지 못했다. 그의 변호사 한스 볼슈타인 역시 아우슈비츠에서 살해되었다.

하우스도르프의 서재는 그의 사위이자 유일한 상속자인 아르투어 쾨니히가 처분했다. 한스 보네가 보존한 하우스도르프의 ''사후 저작물'' 일부는 현재 본 대학교 및 주립 도서관에 소장되어 있으며, 목록화 작업이 이루어져 있다.^[10]

3. 학문적 업적

하우스도르프의 초기 학문적 관심은 수학의 여러 분야에 걸쳐 있었으며, 조건부 확률이나 보험수학 응용 등에 관한 논문을 발표하기도 했다. 그러나 그의 주된 관심은 점차 집합론과 위상수학으로 옮겨갔고, 이는 그의 평생 연구 주제가 되었다.

1901년 라이프치히 대학교에서 교수직을 시작했지만, 당시 팽배했던 노골적인 반유대주의적 분위기 속에서 학문적 성취에도 불구하고 주류 학계에서 순탄한 길을 걷기는 어려웠다. 이러한 환경 속에서도 그는 문학 및 예술 서클에 적극적으로 참여하며 지적 활동을 이어갔다.

그는 집합론의 기초를 가르치며 이 분야에 대한 깊이 있는 연구를 시작했다. 1914년에는 그의 대표적인 저서인 『집합론 기초』(Grundzüge der Mengenlehre|그룬트취게 데어 멩엔레레^de)를 출판하여 집합론 연구의 새로운 기준을 제시했다. 이 책은 현대 집합론과 위상수학의 발전에 큰 영향을 미쳤으며, 특히 책의 후반부에서 다룬 하우스도르프의 역설은 이후 바나흐-타르스키의 역설 증명의 중요한 토대가 되었다.

제1차 세계 대전 이후 그라이프스발트 대학교에 재직할 당시에는 해석학 연구에 집중하여, 1914년 연구를 바탕으로 위상 공간의 차원을 다루는 하우스도르프 차원과 점 집합의 측도를 다루는 하우스도르프 측도 개념을 발전시켰다. 이 개념들은 훗날 프랙탈 기하학의 발전에 중요한 기여를 했다.

1921년 본 대학교로 옮긴 후에도 연구를 계속하여, 1923년에는 자신의 측도론을 공리적 확률론에 적용하는 연구를 발표했다. 그의 논문과 저작들은 명쾌하고 우아한 서술로 정평이 나 있었으며, 신랄하면서도 온화했던 성품은 주변 사람들에게 좋은 인상을 주었다. 『집합론 기초』는 이후에도 계속 개정되어 1927년에는 『집합론』(Mengenlehre|멩엔레레^de)으로 제목을 바꾸어 제2판이, 1935년에는 제3판이 출간되었다.

3. 1. 집합론

하우스도르프가 수학, 특히 집합론과 위상수학으로 관심을 옮긴 것은 그의 학문적 여정에서 중요한 전환점이었다. 그는 집합론의 기초를 가르치기 시작했으며, 이는 곧 방대한 체계를 이루는 연구로 발전했다.

하우스도르프가 순서 집합에 대한 본격적인 연구를 시작한 계기는 칸토어의 연속체 문제, 즉 기수

\aleph = 2^{\aleph_0}

를 알레프 수열

\{\aleph_{\alpha}\}

의 어디에 위치시켜야 하는가 하는 문제였다. 1904년 9월 29일 힐베르트에게 보낸 편지에서 그는 이 문제가 "거의 단일증상처럼 나를 괴롭혔다"고 토로했다.^[11] 하우스도르프는 집합

\mathrm{card} (T(\aleph_0)) = \aleph

을 통해 이 문제를 해결할 새로운 접근법을 모색했다. 칸토어는

\aleph = \aleph_1

이라고 추측했지만

\aleph \geq \aleph_1

만을 증명할 수 있었다. 하우스도르프는

\aleph_1

이 가산 집합의 가능한 정렬 순서의 '수'인 반면,

\aleph

는 모든 가능한 순서의 '수'라는 점에 주목했다. 따라서 그는 정렬 순서보다는 일반적이지만 순서보다는 구체적인 시스템, 즉 '등급 집합'을 연구하기 시작하여 1901년에 관련 논문을 발표했다. 그러나 나중에 쿠르트 괴델과 폴 코언의 연구를 통해, 이 전략 역시 연속체 문제를 해결하지 못한다는 것이 밝혀졌다.

1904년, 하우스도르프는 그의 이름을 딴 재귀 공식

\aleph_{\mu}^{\aleph_{\alpha}} = \aleph_{\mu} \; \aleph_{\mu -1}^{\aleph_{\alpha}}

(모든 비극한 순서수

\mu

에 대해 성립)을 발표했다. 이 공식은 그가 이후 도입한 공종성(cofinality) 개념과 함께 알레프 지수 연구의 기초가 되었다. 같은 해 하이델베르크에서 열린 국제 수학자 회의에서 율리우스 쾨니히는 연속체가 정렬될 수 없으며 따라서 그 기수는 알레프 수가 아니라고 주장하여 큰 논란을 일으켰는데, 하우스도르프는 그의 뛰어난 지식을 바탕으로 쾨니히의 주장에서 오류를 발견하고 이를 명확히 밝혀냈다.^[12]

1906년부터 1909년까지 하우스도르프는 순서 집합에 대한 근본적인 연구를 수행했다. 이 시기에 그는 전체 이론에서 핵심적인 역할을 하는 공종성 개념을 도입했다. 그는 순서수를 더 작은 순서수와 공종이면 정규(regular), 그렇지 않으면 특이(singular)하다고 정의했다. 극한 순서수를 색인하는 정규수가 존재하는지에 대한 그의 질문은 도달 불가능 기수 이론의 출발점이 되었다. 하우스도르프는 그러한 수가 존재한다면 매우 커야 한다는 것을 이미 인지하고 있었다.^[13]

또한, 하우스도르프는 "모든 무경계이고 순서적으로 조밀한 집합

A

에 대해,

A

가

\omega_{\xi}

와 공종이고

\omega_{\eta}^*

(*는 역순서)와 공초(cofinal with the inverse order)가 되는 유일하게 결정된 정규 시작수

\omega_{\xi}, \omega_{\eta}

가 존재한다"는 중요한 정리를 증명했다. 이 정리는 순서 집합의 원소와 간극(gap)을 특성화하는 데 유용하게 사용된다.

하우스도르프는 미리 주어진 문자 집합(원소 및 간극 문자)

W

를 갖는 순서 집합이 존재하는지에 대한 문제를 탐구했다. 그는 필요 조건을 넘어 충분 조건까지 증명해냈는데, 이를 위해 일반 곱(general product)과 거듭제곱(power) 이론을 개발하여 풍부한 순서 집합의 예를 만들어냈다.^[14] 이 과정에서 그는 일반화된 연속체 가설을 처음으로 공식화했으며, 포화 구조의 모형 이론 연구에 중요한 영향을 미친 하우스도르프

\eta_{\alpha}

정규형과 같은 흥미로운 구조를 발견했다.^[15]

일반적인 곱과 기수의 거듭제곱 연구는 하우스도르프를 부분 순서 집합 연구로 이끌었다. 그는 "부분 순서 집합의 모든 전순서 부분 집합이 최대 전순서 부분 집합에 포함되는가?"라는 질문에 대해 정렬 정리를 이용하여 긍정적으로 답했다. 이는 하우스도르프 최대 원리로 알려져 있으며, 선택 공리와 동치임이 밝혀졌다.^[16]

1908년 아르투어 모리츠 쇤플리스는 자신의 집합론 보고서에서 칸토어 이후 발전된 순서 집합 이론이 거의 전적으로 하우스도르프의 공헌에 의한 것이라고 평가했다.^[17]

1914년, 하우스도르프는 그의 기념비적인 저서 『집합론 기초』(''Grundzüge der Mengenlehre'')를 출판했다. 이 책은 곧 집합론의 표준 교과서로 자리 잡았으며, 특히 496페이지 이하에서는 후에 바나흐-타르스키 역설 증명의 기초가 된 "하우스도르프 역설"을 다루었다. 그는 1927년과 1935년에 이 책의 제2판과 제3판을 출판했으며, 제2판부터는 제목을 『집합론』(''Mengenlehre'')으로 변경했다.

3. 2. 위상수학

하우스도르프는 그의 대표적인 저서 『집합론 기초』(Grundzüge der Mengenlehre|그룬트취게 데어 멩엔레레^de, 1914)에서 현대 위상수학의 기초를 다졌다. 이 책의 "점 집합"에 관한 장에서 그는 처음으로 알려진 근방 공리를 기반으로 위상 공간에 대한 체계적인 이론을 개발했으며, 여기에 자신의 이름을 딴 하우스도르프 공간을 추가했다. 이는 이전 수학자들의 접근 방식과 하우스도르프 자신의 공간 문제에 대한 고찰을 종합한 결과였다. 그는 고전적인

\mathbb{R}^n

에서의 점 집합 이론 개념과 정리를 가능한 한 일반적인 경우로 확장하여, 새롭게 만들어진 일반 위상수학 또는 집합론적 위상수학으로 편입시켰다.

하우스도르프는 기존 개념을 일반화하는 것을 넘어, 위상수학의 기본적인 구성 방법들을 개발했다. 여기에는 핵 형성(열린 핵, 자기 조밀 핵)과 껍질 형성(폐포) 등이 포함된다. 또한 그는 열린 집합(그는 이를 "영역"이라 불렀다)의 개념과 모리스 르네 프레셰가 도입한 컴팩트성 개념의 근본적인 중요성을 강조했다. 연결 공간 이론 역시 하우스도르프에 의해 체계적으로 정립되고 발전되었으며, "성분"과 "준성분"이라는 용어를 도입했다.

하우스도르프는 제1 가산 공리와 제2 가산 공리를 도입하여 위상 공간을 더욱 구체화했다. 제1 가산 공리를 만족하는 중요한 공간 유형 중 하나가 거리 공간이다. 거리 공간은 1906년 프레셰에 의해 "클래스(E)"라는 이름으로 처음 소개되었지만, "거리 공간"이라는 용어는 하우스도르프가 『집합론 기초』에서 사용하면서 널리 퍼졌다. 그는 이 책에서 거리 공간 이론을 체계적으로 발전시켰고, 하우스도르프 거리, 완비성, 전 유계,

\rho

-연결성, 환원 가능한 집합 등 새로운 개념들을 도입하여 이론을 풍부하게 만들었다. 프레셰의 연구는 상대적으로 덜 알려졌지만, 하우스도르프의 저서를 통해 거리 공간은 수학자들에게 필수적인 개념으로 자리 잡게 되었다.

또한 하우스도르프는 해석학 연구를 통해 1914년 위상 공간의 차원 개념인 하우스도르프 차원과 점 집합의 외측도인 하우스도르프 측도를 도입했다. 이 개념들은 이후 프랙탈 기하학 발전에 중요한 토대를 제공했다.^[18]

『집합론 기초』는 제1차 세계 대전 직전에 출판되어 초기에는 큰 주목을 받지 못했으나, 전쟁 후 젊은 세대 연구자들에게 막대한 영향을 미쳤다. 특히 1920년 폴란드에서 창간된 저널 ''Fundamenta Mathematicae''는 하우스도르프의 아이디어를 확산시키는 데 중요한 역할을 했다. 이 저널의 초기 논문들에서 『집합론 기초』는 빈번하게 인용되었으며, 그의 개념들은 점차 수학계의 표준으로 자리 잡았다. 파벨 알렉산드로프와 파벨 우리손이 설립한 러시아 위상수학 학파 역시 하우스도르프의 저서에 크게 의존했으며, 알렉산드로프와 우리손의 공동 연구인 ''칸토르 다양체에 관한 연구''^[19]에서는 『집합론 기초』가 60번 이상 인용될 정도로 그 영향력이 깊었다. 제2차 세계 대전 이후에도 이 책에 대한 수요는 꾸준히 이어져 여러 차례 재판되었다.

3. 3. 측도론 및 함수해석학

1916년, 알렉산드로프와 하우스도르프는 보렐 집합에 대한 연속체 가설을 독립적으로 해결했다.^[20] 이 결과는 완전 가분 거리 공간의 모든 보렐 집합은 가산적이거나 연속체의 기수를 갖는다는 내용으로, 이는

\mathbb{R}^n

의 닫힌 집합에 대해 성립하는 칸토어-벤딕슨 정리를 일반화한 것이다. 선형

G_{\delta}

집합에 대해서는 W.H. 영이 1903년에 이미 증명했고,^[21] 하우스도르프 자신도 1914년 저서 ''원리''에서

G_{\delta\sigma\delta}

집합에 대해 유사한 결과를 얻은 바 있다. 알렉산드로프와 하우스도르프의 이 정리는 이후 기술 집합론의 발전에 큰 영향을 미쳤다.^[22]

하우스도르프가 그라이프스발트 대학에 재직하던 시절 발표한 연구 중 1919년의 "차원과 외측도"는 특히 중요한 업적으로 평가받는다. 이 논문에서 오늘날 하우스도르프 측도와 하우스도르프 차원으로 불리는 개념이 처음 소개되었다. 이 개념들은 매우 불규칙한 형태를 가진 집합의 '크기'나 '차원'을 수학적으로 정의하고 비교하는 방법을 제공했으며, 발표 이후 현대 수학의 여러 분야에서 중요하게 활용되고 있다. 특히 동역학계 이론, 기하학적 측도론, 자기 유사 집합 및 프랙탈 이론, 확률 과정 이론, 조화 해석, 전위 이론, 수론 등 다양한 분야에서 응용되고 발전했다.^[23]

본 대학에서 두 번째 임기를 보내는 동안 하우스도르프는 해석학 분야에서도 중요한 연구 성과를 남겼다. 1921년 논문 "합산 방법과 모멘트 수열 I"에서는 발산하는 급수를 다루는 새로운 방법들의 체계, 즉 오늘날 하우스도르프 방법이라고 불리는 것을 개발했다. 이 방법은 기존의 횔더 방법이나 체사로 방법 등을 특수한 경우로 포함하는 일반적인 이론이다. 하디는 그의 유명한 저서 ''발산 급수''에서 하우스도르프 방법을 상세히 소개하기도 했다. 하우스도르프는 이 방법을 모멘트 수열과 연결하여, 유한한 구간에서의 모멘트 문제를 푸는 새로운 접근법을 제시했다. 1923년 논문 "유한 구간에 대한 모멘트 문제"에서는 특정 조건을 만족하는 함수에 대한 모멘트 문제를 더 깊이 연구했다. 모멘트 문제의 해의 존재성과 유일성에 대한 연구는 하우스도르프가 오랫동안 몰두했던 주제였다.^[24]

1920년대에 새롭게 부상하던 함수해석학 분야에도 기여했다. 1923년 논문 "푸리에 급수에 대한 파르세발 정리의 확장"에서 하우스도르프는 리이즈-피셔 정리를 L^p 공간이라는 더 일반적인 함수 공간으로 확장했다. 또한 이 논문에서 W.H. 영과 함께 하우스도르프-영 부등식으로 알려진 중요한 부등식을 증명했다. 이 부등식은 이후 함수해석학 분야의 여러 중요한 발전들의 출발점이 되었다.^[25]

3. 4. 확률론

하우스도르프는 초기에 수학 분야에서 확률론에 관심을 두었다. 그는 조건부 확률, 보험수학에의 응용 등에 관한 논문을 발표했다. 이후 그의 주요 연구 관심사는 집합론과 위상수학으로 옮겨갔으며, 이 분야들은 그의 오랜 연구 주제가 되었다.

3. 5. 하우스도르프의 역설

하우스도르프는 1914년에 『집합론 기초』(Grundzüge der Mengenlehre^deu)를 출판했는데, 이 책은 집합론의 표준적인 저서가 되었다. 이 책의 496페이지 이하에는 하우스도르프의 역설에 대한 내용이 실려 있다. 이 역설적인 결과는 나중에 바나흐-타르스키의 역설 증명에 중요한 기초를 제공했다.

4. 저술 활동 (파울 몽그레)

하빌리타치온 이후 라이프치히 대학교 강사로 재직하며 수학 연구와 강의에 힘쓰는 한편, Paul Mongré|파울 몽그레^de라는 필명으로 문학 및 철학 분야에서도 활발한 활동을 펼쳤다. 그는 다양한 분야에 관심을 가졌으며, 헤르만 콘라디, 리하르트 데멜, 막스 클링거, 프랑크 베데킨트 등 당대의 저명한 작가, 예술가들과 교류했다.

특히 1897년부터 1904년까지는 그의 문학적, 철학적 창작 활동이 가장 왕성했던 시기로, 이 기간 동안 발표된 22개의 필명 작품 중 18개가 출판되었다. 그는 이 필명으로 격언집, 인식론 연구서, 시집, 희곡 등 다양한 장르의 글을 발표했으며, 상류 계급의 관습을 풍자하기도 했다.

파울 몽그레 명의의 주요 저술은 다음과 같다.

파울 몽그레 명의 주요 저술
연도	제목 (원제)	비고 (장르/게재지)
1897	산틸라리오. 자라투스트라의 풍경에서 나온 생각. Sant' Ilario. Gedanken aus der Landschaft Zarathustras^de	경구집
1898	우주적 선택에서의 혼돈 - 인식론적 시도. Das Chaos in kosmischer Auslese – Ein erkenntniskritischer Versuch^de	인식론 연구서
1898	대중의 행복과 개인의 행복. Das individuelle Leid und das Allgemeinwohl^de	에세이 (Neue Deutsche Rundschau)
1898	부정한 세기. Das unsaubere Jahrhundert^de	에세이 (Neue Deutsche Rundschau)
1900	엑스터시. Ekstasen^de	시집
1902	권력 의지. Der Wille zur Macht^de	에세이 (Neue Deutsche Rundschau)
1902	막스 클링거의 베토벤. Max Klingers Beethoven^de	예술 비평 (Zeitschrift für bildende Kunst)
1903	언어 비판 Sprachkritik^de	에세이 (Neue Deutsche Rundschau)
1904	그의 명예의 의사, 그로테스크. Der Arzt seiner Ehre, Groteske^de	희곡

그의 저술 중 ''산틸라리오''의 부제나 '권력 의지'에 대한 에세이는 당대 지성계에 큰 영향을 미친 니체 철학에 대한 하우스도르프의 깊은 관심을 보여준다. 제1차 세계 대전 이후의 사전에서는 그를 저명한 수학자이자 작가로 기록하기도 했다.

5. 유산 및 평가

하우스도르프의 이름은 수학계 전반에 걸쳐 그의 업적을 기리기 위해 사용되고 있다. 그의 이름을 딴 주요 개념들은 다음과 같다.

하우스도르프 완비화
하우스도르프 수렴
하우스도르프 밀도
하우스도르프 차원
하우스도르프 거리
하우스도르프 갭
하우스도르프 극대 원리
하우스도르프 측도
하우스도르프 모멘트 문제
하우스도르프 역설
하우스도르프 공간
하우스도르프-영 부등식
베이커-캠벨-하우스도르프 공식

또한, 여러 교육 및 연구 기관에도 그의 이름이 붙여졌다.

본의 하우스도르프 수학 센터
본의 ''하우스도르프 수학 연구소''
그라이프스발트의 ''펠릭스 하우스도르프 국제 만남 센터''

그가 활동했던 도시들에는 그의 이름을 딴 거리가 존재한다. 독일 본에는 그가 처음 살았던 집(61번지)이 있는 하우스도르프 거리(Hausdorffstraße^de)가 있으며, 그라이프스발트에는 여러 연구소가 위치한 펠릭스-하우스도르프 거리(Felix-Hausdorff–Straße^de)가 있다. 2011년부터는 라이프치히 골리스 지구에 하우스도르프 길(Hausdorffweg^de)이 조성되었다.

천문학 분야에서도 그의 이름이 기려져, 소행성 24947 하우스도르프가 그의 이름을 따서 명명되었다.

하우스도르프는 1935년 독일에서 나치즘이 극심해지던 시기에 교수직에서 강제로 물러나야 했다. 유대인이었던 그는 출국을 원치 않았고, 동료와 제자들이 독일을 떠나거나 전쟁으로 희생되는 상황 속에서도 본에 머물렀다. 결국 1942년, 유대인 수용소 이송이 결정되자 하우스도르프는 아내, 그리고 아내의 여동생과 함께 스스로 목숨을 끊는 비극적인 선택을 했다. 이는 나치즘 정권 하에서 유대인 지식인이 겪어야 했던 억압과 절망적인 상황을 보여준다.

참조

_[1] 웹사이트 Hausdorff space Definition & Meaning https://www.dictiona[...] 2022-06-15
_[2] 웹사이트 Felix Hausdorff - Paul Mongré http://hausdorff-edi[...] 2023-11-14
_[3] 논문 Biographie. Felix Hausdorff, Gesammelte Werke. Band IB. By Egbert Brieskorn and Walter Purkert 2021
_[4] 문서 Archiv der Universität Leipzig, PA 547
_[5] 서적 Handbook of the History of Logic: Sets and extensions in the twentieth century https://books.google[...] Elsevier 2012-01-01
_[6] 문서 Neuenschwander, E.: ''Felix Hausdorffs letzte Lebensjahre nach Dokumenten aus dem Bessel-Hagen-Nachlaß''. In: Brieskorn 1996, S. 253–270.
_[7] 문서 Schubring, G. (2021). Biographie. Felix Hausdorff, Gesammelte Werke. Band IB. by Egbert Brieskorn and Walter Purkert. Math Intelligencer 43, 94–98
_[8] 문서 Nachlass Bessel-Hagen, Universitätsarchiv Bonn. Abgedruckt in Brieskorn 1996, S. 263–264 und im Faksimile S. 265–267
_[9] 문서 de:Abschiedsbrief Felix Hausdorffs
_[10] 문서 Siehe Findbuch Nachlass Hausdorff
_[11] 문서 Niedersächsische Staats- und Universitätsbibliothek zu Göttingen, Handschriftenabteilung, NL Hilbert, Nr. 136.
_[12] 문서 Detaillierte Angaben findet man in den gesammelten Werken, Band II, S. 9–12.
_[13] 서적 H.: Gesammelte Werke. Band II: ''Grundzüge der Mengenlehre.'' Springer-Verlag, Berlin, Heidelberg etc. 2002. Kommentare von U. Felgner, S. 598–601.
_[14] 서적 H.: Gesammelte Werke. Band II: ''Grundzüge der Mengenlehre.'' Springer-Verlag, Berlin, Heidelberg etc. 2002. S. 604–605.
_[15] 서적 Siehe dazu den Essay von U. Felgner: ''Die Hausdorffsche Theorie der $\eta_{\alpha}$ -Mengen und ihre Wirkungsgeschichte'' in H.: Gesammelte Werke. Band II: ''Grundzüge der Mengenlehre''. Springer-Verlag, Berlin, Heidelberg etc. 2002. S. 645–674.
_[16] 서적 Siehe dazu und zu ähnlichen Sätzen von [[Kazimierz Kuratowski|Kuratowski]] und [[Max August Zorn|Zorn]] den Kommentar von U. Felgner in den gesammelten Werken, Band II, S. 602–604.
_[17] 서적 Schoenflies, A.: ''Die Entwickelung der Lehre von den Punktmannigfaltigkeiten.'' Teil II. Jahresbericht der DMV, 2. Ergänzungsband, Teubner, Leipzig 1908., S. 40.
_[18] 서적 For the history of Haussdorff's sphere paradox see ''Gesammelte Werke Band IV'', S. 11–18; also the article by P. Schreiber in Brieskorn 1996, S. 135–148, and the monograph Wagon 1993.
_[19] 논문 Mémoire sur les multiplicités Cantoriennes. http://matwbn.icm.ed[...] 1925
_[20] 논문 Sur la puissance des ensembles mesurables B. 1916
_[21] 논문 Zur Lehre der nicht abgeschlossenen Punktmengen 1903
_[22] 서적 Alexandorff, Hopf 1935, S. 20. For details see ''Gesammelte Werke Band II'', S. 773–787.
_[23] 문서 For the history of the reception of ''Dimension und äußeres Maß'', see the article by Bandt/Haase and Bothe/Schmeling in Brieskorn 1996, S. 149–183 and S. 229–252 and the commentary of S. D. Chatterji in ''Gesammelten Werken, Band IV'', S. 44–54 and the literature given there.
_[24] 문서 ''Gesammelte Werke Band IV'', S. 105–171, 191–235, 255–267 and 339–373.
_[25] 문서 See commentary by S. D. Chatterji in ''Gesammelten Werken Band IV'', S. 182–190.
_[26] 논문 F. Hausdorff, Mengenlehre 1928
_[27] 간행물 Ratsversammlung vom 18. Mai 2011 (Beschluss-Nr. RBV-822/11), amtliche Bekanntmachung: Leipziger Amtsblatt Nr. 11 vom 4. Juni 2011, bestandskräftig seit dem 5. Juli 2011 bzw. 5. August 2011. Vgl. Leipziger Amtsblatt Nr. 16 vom 10. September 2011.
_[28] 웹사이트 Review von Jeremy Gray der Bände 1a, 3, 8, 9, Bulletin AMS, Band 51, 2014, 169–172. https://www.ams.org/[...]
_[29] 논문 Review: ''Gesammelte Werke'', Vols. II, IV, V, and VII, by Felix Hausdorff https://www.ams.org/[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com