표준 오차
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
표준 오차는 표본 통계량의 불확실성을 측정하는 지표로, 표본 평균이 모집단 평균에서 얼마나 떨어져 있는지 추정하는 데 사용된다. 모집단의 표준 편차와 표본 크기에 따라 계산되며, 표본 크기가 커질수록 표준 오차는 감소한다. 표준 오차는 신뢰 구간 계산, 가설 검정 등 다양한 통계적 추론에 활용되며, 여론조사, 사회과학, 의학 연구 등에서 표본 데이터를 통해 모집단의 특성을 추론하는 데 중요한 역할을 한다.
더 읽어볼만한 페이지
- 통계 분석 - 베셀 보정
베셀 보정은 모집단 평균을 모를 때 표본 분산으로 모집단 분산을 추정하며 발생하는 편향을 수정하기 위해 n/(n-1)을 곱하는 방법이다.
| 표준 오차 | |
|---|---|
| 통계적 속성 | |
| 정의 | 표본 통계량의 표본 분포의 표준 편차 |
| 사용 | 모집단 모수에 대한 추정의 정확성 측정 |
| 계산 | |
| 평균의 표준 오차 (SEM) | σ / √n (σ는 모집단 표준 편차, n은 표본 크기) |
| 표준 오차 추정 | s / √n (s는 표본 표준 편차, n은 표본 크기) |
| 오해 | |
| 오해 | 표본의 변동성을 반영하는 표준 편차와 혼동될 수 있음 |
| 활용 | |
| 가설 검정 | 검정 통계량 계산 및 p-값 결정에 사용 |
| 신뢰 구간 | 모집단 모수에 대한 신뢰 구간 설정에 사용 |
| 주의 사항 | |
| 표본 크기 | 표본 크기가 클수록 표준 오차가 작아짐 (추정의 정확성 증가) |
| 모집단 분포 | 중심 극한 정리에 따라 표본 크기가 충분히 크면 표본 평균의 분포는 정규 분포에 근사함 |
| 관련 개념 | |
| 표준 편차 | 데이터의 흩어진 정도를 나타내는 척도 |
| 신뢰 구간 | 모수가 포함될 것으로 예상되는 범위 |
| 가설 검정 | 모집단에 대한 주장을 검증하는 통계적 방법 |
| 추가 정보 | |
| 다른 이름 | 평균의 표준 오차 (SEM) |
| 관련 분야 | 통계학 계량경제학 생물통계학 |
2. 정의
표준 오차는 표본 평균의 표준 편차로, 표본 평균이 모집단 평균에서 얼마나 벗어날 수 있는지 나타내는 지표이다. 모집단 표준 편차 ''σ'', 모집단 크기 ''N''에서 표본 크기 ''n''개를 비복원 추출할 때, 표준 오차는 다음 식으로 추정된다.
:
표본 데이터에서 계산한 표준 편차 ''s''로 ''σ''를 추정하는 경우에는
:
가 된다.
모집단 크기 ''N''이 충분히 큰 경우에는
: 또는
로 근사할 수 있다.
표준 오차는 표본 크기의 제곱근에 반비례한다. 즉, 표본 크기를 4배로 늘리면 표준 오차는 절반으로 줄어든다. 통계 조사 계획 시, 비용과 노력을 고려하여 오차를 최소화할 때 이 관계식이 중요하다.
일본 산업 규격에서는 표준 오차를 "추정량의 표준 편차"로 정의한다.
2. 1. 기본 정의
표본 모집단에서 표준 편차 로 추출된 통계적으로 독립적인 개의 관측치 의 표본이 있다고 가정한다. 표본에서 계산된 평균값 는 ''평균에 대한 표준 오차'' 와 관련되며, 표준 오차는 다음과 같이 정의된다.[1]:
이는 모집단 평균의 값을 추정하려고 할 때, 인수로 인해, 추정 오차를 2의 인수로 줄이려면 표본에서 4배 더 많은 관측치를 얻어야 함을 의미한다. 10의 인수로 줄이려면 100배 더 많은 관측치가 필요하다.
표준 오차는 독립적인 확률 변수 합의 분산으로부터 유도될 수 있으며,[6] 분산의 정의와 몇 가지 속성이 주어진다.
일본 산업 규격에서는, "추정량의 표준 편차"로 표준 오차를 정의하고 있다.
2. 2. 유한 모집단 수정
모집단 크기가 N으로 유한하고, 비복원 추출로 표본 추출이 이루어질 때, 표준 오차는 다음과 같이 수정된다.[10][11]표준 편차 ''σ'', 요소 수 ''N''의 모집단에서 ''n''개의 표본을 추출할 때, 표준 오차는 다음 식으로 추정된다.
:
표준 편차 ''σ''를 표본 데이터에서 계산한 표준 편차 ''s''로 추정하는 경우에는
:
가 된다.
''N''이 충분히 큰 경우에는
: 또는
로 해도 좋다.
이는 큰 ''N''에 대해 다음과 같이 근사할 수 있다.
:
이는 모집단의 더 큰 비율에 가깝게 표본 추출함으로써 얻는 추가적인 정밀도를 고려하기 위함이다. FPC의 효과는 표본 크기 ''n''이 모집단 크기 ''N''과 같을 때 오차가 0이 된다는 것이다.
이것은 조사 방법론에서 비복원 추출로 표본 추출할 때 발생한다. 복원 추출을 하는 경우에는 FPC가 적용되지 않는다.
표준 오차는 추출하는 표본 크기의 제곱근에 반비례한다. 즉, 표본 크기를 4배로 하면 표준 오차를 절반으로 줄일 수 있다. 통계 조사를 계획할 때, 비용이나 노력을 어느 범위 내에 수렴시킨 후 오차를 최소화하고 싶은 경우가 많은데, 이러한 조건들의 관계를 판단하는 데에 위의 관계식이 중요하다.
3. 중심극한정리와의 관계
중심극한정리는 모집단에서 취한 표본 평균값의 분포가 표본 수가 커질수록 평균값을 중심으로 하는 정규 분포에 가까워진다는 통계학적 원리이다.
3. 1. 중심극한정리의 예시
모집단에서 취한 표본 평균값의 분포는 표본 수가 커질수록 평균값을 중심으로 하는 정규 분포에 가까워진다는 중심극한정리(中心極限定理)의 예는 다음과 같다.표준편차의 정의에 의해서 확률변수 의 모 집단의 표준 편차 는 다음과 같다.
:
분산의 정의에 의해서 확률변수 의 기댓값(혹은 평균) 일 때, 분산 는 다음과 같다.
:
따라서 표본 평균(sample mean) 는 다음과 같다.
:
:
:
:
:
:
:
:
:
:
:
:
:
4. 표준 오차의 추정
실제 상황에서는 모집단의 표준 편차(σ)를 알 수 없는 경우가 대부분이다. 표준 편차 ''σ'', 요소 수 ''N''의 모집단에서 ''n''개의 표본을 추출할 때, 표준 오차는 다음 식으로 추정된다.
:
표준 편차 ''σ''를 표본 데이터에서 계산한 표준 편차 ''s''로 추정하는 경우에는
:
가 된다.
''N''이 충분히 큰 경우에는
: 또는
로 해도 좋다.
이 식에서 중요한 점은, 표준 오차는 추출하는 표본 크기의 제곱근에 반비례한다는 것이다. 예를 들어 표본 크기를 4배로 하면 표준 오차를 절반으로 줄일 수 있다. 통계 조사를 계획할 때, 비용이나 노력을 어느 범위 내에 수렴시킨 후 오차를 최소화하고 싶은 경우가 많은데, 이러한 조건들의 관계를 판단하는 데에 위의 관계식이 중요하다.
일본 산업 규격에서는, "추정량의 표준 편차"로 표준 오차를 정의하고 있다.[1]
4. 1. 표본 표준 편차를 이용한 추정
모집단의 표준 편차 는 거의 알려져 있지 않다. 따라서 평균의 표준 오차는 일반적으로 를 표본 표준 편차 로 대체하여 추정한다.:
이는 참 "표준 오차"에 대한 단지 하나의 추정량이므로, 다음과 같은 다른 표기법을 사용하는 경우도 흔히 볼 수 있다.
:
다음 사항들을 명확하게 구분하지 못할 때 흔히 혼란이 발생한다.
- ''모집단''의 표준 편차(),
- ''표본''의 표준 편차(),
- ''평균'' 자체의 표준 편차(, 이는 표준 오차), 그리고
- 평균의 표준 편차의 ''추정량''(, 이는 가장 흔히 계산되는 양이며, 구어체로 흔히 "표준 오차"라고도 한다).
표준 편차 ''σ'', 요소 수 ''N''의 모집단에서 ''n''개의 표본을 추출할 때, 표준 오차는 다음 식으로 추정된다.
:
표준 편차 ''σ''를 표본 데이터에서 계산한 표준 편차 ''s''로 추정하는 경우에는
:
가 된다.
''N''이 충분히 큰 경우에는
: 또는
로 해도 좋다.
이 식에서 중요한 점은, 표준 오차는 추출하는 표본 크기의 제곱근에 반비례한다는 것이다. 즉, 예를 들어 표본 크기를 4배로 하면 표준 오차를 절반으로 줄일 수 있다. 통계 조사를 계획할 때, 비용이나 노력을 어느 범위 내에 수렴시킨 후 오차를 최소화하고 싶은 경우가 많다. 이러한 조건들의 관계를 판단하는 데에 위의 관계식이 중요하다.
4. 2. 추정의 정확도
모집단의 표준 편차 \(\sigma\)는 거의 알려져 있지 않다. 따라서 평균의 표준 오차는 일반적으로 \(\sigma\)를 표본 표준 편차 \(\sigma_{x}\)로 대체하여 추정한다.:\(\sigma_\bar{x} \approx \frac{\sigma_{x}}{\sqrt{n}}.\)
이는 참 "표준 오차"에 대한 단지 하나의 추정량이므로, 다음과 같은 다른 표기법을 사용하는 경우도 흔히 볼 수 있다.
:\(\widehat{\sigma}_{\bar{x}}} := \frac{\sigma_{x}}{\sqrt{n}} \qquad \text{ or } \qquad {s}_\bar{x} := \frac{s}{\sqrt{n}}.\)
다음 사항들을 명확하게 구분하지 못할 때 흔히 혼란이 발생한다.
- ''모집단''의 표준 편차(\(\sigma\)),
- ''표본''의 표준 편차(\(\sigma_{x}\)),
- ''평균'' 자체의 표준 편차(\(\sigma_{\bar{x}}\), 이는 표준 오차), 그리고
- 평균의 표준 편차의 ''추정량''(\(\widehat{\sigma}_{\bar{x}}\), 이는 가장 흔히 계산되는 양이며, 구어체로 흔히 "표준 오차"라고도 한다).
표본 크기가 작을 때, 모집단의 실제 표준 편차 대신 표본의 표준 편차를 사용하면 모집단 표준 편차와 표준 오차를 체계적으로 과소 추정하는 경향이 있다. n = 2인 경우, 과소 추정은 약 25%이지만, n = 6인 경우 과소 추정은 5%에 불과하다. Gurland와 Tripathi (1971)는 이러한 효과에 대한 보정 및 방정식을 제공한다.[4] Sokal과 Rohlf (1981)는 n < 20인 작은 표본에 대한 보정 계수의 방정식을 제공한다.[5] 자세한 내용은 표준 편차의 불편 추정량을 참조하십시오.
표준 오차는 추출하는 표본 크기의 제곱근에 반비례한다. 즉, 예를 들어 표본 크기를 4배로 하면 표준 오차를 절반으로 줄일 수 있다.
5. 신뢰 구간
표준 오차()는 모집단 평균의 신뢰 구간을 추정하는 데 사용된다. 표준 오차는 값의 불확실성을 측정하는 간단한 척도를 제공하며, 다음과 같은 이유로 자주 사용된다.
- 여러 개별 양의 표준 오차가 알려져 있다면, 해당 양의 일부 함수의 표준 오차를 쉽게 계산할 수 있다.
- 값의 확률 분포가 알려져 있으면, 이를 사용하여 정확한 신뢰 구간을 계산할 수 있다.
- 확률 분포가 알려져 있지 않은 경우, 체비쇼프 부등식 또는 비소찬스키-페투닌 부등식을 사용하여 보수적인 신뢰 구간을 계산할 수 있다.
- 표본 크기가 무한대에 가까워지면, 중심 극한 정리에 의해 평균의 표본 분포가 점근적으로 정규 분포를 따른다는 것이 보장된다.
5. 1. 정규 분포를 따르는 경우
표본 분포가 정규 분포를 따르는 경우, 표본 평균, 표준 오차, 그리고 정규 분포의 분위수를 사용하여 실제 모집단 평균에 대한 신뢰 구간을 계산할 수 있다. 다음 식을 사용하여 상위 및 하위 95% 신뢰 한계를 계산할 수 있다. 여기서 는 표본 평균, 는 표본 평균의 표준 오차, 1.96은 정규 분포의 97.5 백분위수 지점의 근사값이다.:상위 95% 한계 =
:하위 95% 한계 =
분포가 정규 분포를 따르는 경우, 95% 신뢰 구간은 대략 평균 ± 2×표준 오차, 99% 신뢰 구간은 대략 평균 ± 3×표준 오차가 된다.
5. 2. 스튜던트 t-분포를 이용한 근사
참된 기본 분포가 정규 분포로 알려져 있지만, σ(모집단 표준편차)를 알 수 없는 경우, 추정된 분포는 스튜던트 t-분포를 따른다. 표준 오차는 스튜던트 t-분포의 표준 편차이다. T-분포는 정규 분포와 약간 다르며, 표본 크기에 따라 달라진다. 작은 표본은 모집단 표준 편차를 과소평가하고 참된 모집단 평균과 다른 평균을 가질 가능성이 다소 높으며, 스튜던트 t-분포는 정규 분포에 비해 다소 더 두꺼운 꼬리를 가진 이러한 사건의 확률을 고려한다. 스튜던트 t-분포의 표준 오차를 추정하기 위해 σ 대신 표본 표준 편차 "s"를 사용하는 것만으로 충분하며, 이 값을 사용하여 신뢰 구간을 계산할 수 있다.[1]Student 확률 분포는 표본 크기가 100을 초과할 때 정규 분포로 근사할 수 있다. 이러한 표본의 경우, 더 간단한 정규 분포를 사용할 수 있다.[1]
6. 표본 크기와 표준 오차
표준 오차는 추출하는 표본 크기의 제곱근에 반비례한다. 예를 들어 표본 크기를 4배로 하면 표준 오차를 절반으로 줄일 수 있다. 통계 조사를 계획할 때, 비용이나 노력을 어느 범위 내에 수렴시킨 후 오차를 최소화하고 싶은 경우가 많은데, 이러한 조건들의 관계를 판단하는 데에 표준 오차와 표본 크기의 관계식이 중요하다.
7. 표본의 상관관계 보정
측정값들이 통계적으로 독립적이지 않은 경우, 표준 오차를 보정해야 한다.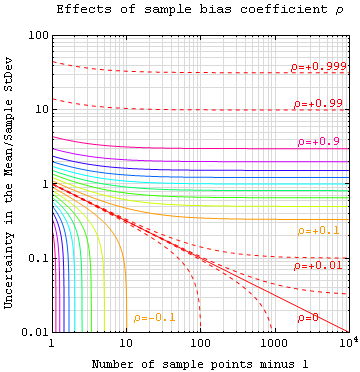
측정량 ''A''의 값이 통계적으로 독립적이지 않고 파라미터 공간 '''x'''의 알려진 위치에서 얻은 경우, 평균의 실제 표준 오차(실제로 표준 편차 부분의 보정)에 대한 비편향 추정치를 표본의 계산된 표준 오차에 특정 인자를 곱하여 얻을 수 있다. 이와 관련한 자세한 내용은 표준 편차의 비편향 추정을 참조할 수 있다.[12]
7. 1. 자기 상관 계수를 이용한 보정
측정값 ''A''가 통계적으로 독립적이지 않고, 파라미터 공간 '''x'''의 알려진 위치에서 얻은 경우, 평균의 실제 표준 오차(실제로 표준 편차 부분의 보정)에 대한 비편향 추정치를 얻을 수 있다. 이는 표본의 계산된 표준 오차에 다음 인자 ''f''를 곱하여 계산할 수 있다.[12]:
여기서 표본 편향 계수 ρ는 모든 표본 점 쌍에 대한 자기상관 계수(-1과 +1 사이의 값)의 Prais–Winsten 추정치이다. 이 근사 공식은 중간에서 큰 표본 크기에 적용된다. 모든 표본 크기에 대한 정확한 공식은 참고 자료에 나와 있으며, 월스트리트 주식 시세와 같이 심하게 자기상관된 시계열에 적용할 수 있다. 또한 이 공식은 양수와 음수 ρ 모두에 적용된다.[12] 자세한 내용은 표준 편차의 비편향 추정 문서를 참고하라.
7. 2. 개념 비교
다음 사항들을 명확하게 구분하지 못할 때 혼란이 발생한다.[8]- '''모집단'''의 표준 편차()
- '''표본'''의 표준 편차()
- '''평균''' 자체의 표준 편차(, 이는 표준 오차)
- 평균의 표준 편차의 '''추정량'''(, 이는 가장 흔히 계산되는 양이며, 구어체로 흔히 "표준 오차"라고도 함)
과학 및 기술 문헌에서 실험 데이터는 표본 데이터의 평균 및 표준 편차 또는 평균과 표준 오차를 사용하여 요약되는 경우가 많다. 그러나 평균과 표준 편차는 기술 통계인 반면, 평균의 표준 오차는 임의 표본 추출 과정에 대한 설명이다. 표본 데이터의 표준 편차는 측정값의 변동에 대한 설명인 반면, 평균의 표준 오차는 중심 극한 정리에 비추어 표본 크기가 모집단 평균의 추정치에 대해 얼마나 더 나은 경계를 제공할지에 대한 확률적 진술이다.[8]
간단히 말해서, 표본 평균의 '''표준 오차'''는 표본 평균이 모집단 평균에서 얼마나 멀리 떨어져 있을지에 대한 추정치인 반면, 표본의 '''표준 편차'''는 표본 내 개별 값들이 표본 평균과 얼마나 다른지를 나타내는 정도이다.[9] 모집단 표준 편차가 유한하다면, 표본의 크기가 증가함에 따라 표본 평균의 표준 오차는 0에 가까워지는 경향이 있다. 이는 모집단 평균의 추정치가 개선되기 때문이며, 표본 크기가 증가함에 따라 표본의 표준 편차는 모집단 표준 편차에 근접하는 경향이 있다.
8. 활용 및 주의사항
표준 오차는 통계적 추론, 가설 검정, 신뢰 구간 추정 등 다양한 분야에서 활용된다. 특히, 여론조사, 사회과학 연구, 의학 연구 등에서 표본 데이터를 기반으로 모집단의 특성을 추론할 때 중요한 역할을 한다.
참조
[1]
학술지
Standard deviations and standard errors
2005-10-15
[2]
서적
The Cambridge Dictionary of Statistics
Cambridge University Press
[3]
학술지
What is a standard error? (And how should we compute it?)
https://www.scienced[...]
2023
[4]
학술지
A simple approximation for unbiased estimation of the standard deviation
[5]
서적
Biometry: Principles and Practice of Statistics in Biological Research
https://archive.org/[...]
[6]
서적
Essentials of Statistical Methods, in 41 pages
Rumsby
[7]
서적
Probability, Statistics, and Decisions for Civil Engineers
McGraw-Hill
[8]
학술지
What to use to express the variability of data: Standard deviation or standard error of mean?
[9]
서적
Biostatistics and Epidemiology : A Primer for Health Professionals
https://books.google[...]
Springer
[10]
학술지
On the value of a mean as calculated from a sample
https://zenodo.org/r[...]
[11]
학술지
The Standard Error of the Mean and the Difference Between Means for Finite Populations
[12]
학술지
Analysis of Short Time Series: Correcting for Autocorrelation
https://zenodo.org/r[...]
[13]
문서
Everitt, B.S. (2003) ''The Cambridge Dictionary of Statistics'', CUP.
[14]
서적
측량학1
형설출판사
2013
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com