프루드 수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 역사
4. 상류, 사류, 한계류
5. 다양한 분야에서의 활용
6. 무차원화된 나비에-스토크스 방정식
7. 한국의 관점
참조

1. 개요

프루드 수(Fr)는 유체 역학에서 사용되는 무차원 수로, 유체의 관성력과 중력의 비를 나타낸다. 정의는 평균 유속, 중력 가속도, 수리 평균 심을 사용하여 표현되거나, 특성 속도, 특성 길이, 중력 가속도를 사용하여 표현된다. 프루드 수는 개수로 흐름, 선박 유체역학, 얕은 물에서의 파동, 풍공학, 지구물리적 질량 흐름, 교반 탱크, 입자 베드 거동, 생체 역학 등 다양한 분야에서 활용된다. 특히 선박의 조파 저항, 흐름의 상류/사류/한계류 구분, 동물의 보행 패턴 연구 등에 중요한 지표로 사용되며, 나비에-스토크스 방정식을 무차원화하는 데에도 사용된다.

더 읽어볼만한 페이지

수리공학 - 우물
우물은 식수와 관개용으로 사용된 지하수 취수 구조물로, 다양한 재료와 기술로 건설되었으며 깊이와 용도에 따라 여러 종류로 나뉘지만, 오염과 고갈 문제, 사회·문화적 기능 약화라는 과제를 안고 있어 지속 가능한 이용을 위한 노력이 필요하다.
수리공학 - 펌프
펌프는 공기나 액체를 흡입하여 토출하는 기계이며, 진공과 고압을 이용해 작동하고, 원심 펌프, 기어 펌프 등 다양한 종류가 있으며, 효율, 양정, 유량 등으로 성능을 평가하여 산업 전반에 사용된다.
유체역학 - 양력
양력은 유체 속에서 물체가 받는 수직 방향의 힘이며, 받음각, 익형, 공기 밀도 등에 따라 달라지며 항공기 날개, 헬리콥터, 선박 프로펠러 등에서 활용된다.
유체역학 - 무인 항공기
무인 항공기는 조종사 없이 자율 또는 원격 조종으로 비행하는 동력 비행체로, 다양한 기준으로 분류되어 군사 및 민간용으로 활용되지만 안전 및 보안 위협, 사이버 공격, 악의적 사용 가능성 등의 문제점도 존재한다.

프루드 수

2. 정의

프루드 수(Fr^영어)는 다음과 같이 정의된다.

: $Fr = \frac{V}{\sqrt{gD}}$

''V'' : 평균 유속
''g'' : 중력 가속도
''D'' : 수리평균심 ()
''A'' : 통수단면적
''B'' : 수로폭^[8]

유체역학뿐만 아니라 일반적인 연속체 역학에도 프루드 수가 어떻게 연결되는지를 보기 위해, 코시 운동량 방정식을 무차원 형태로 나타낼 수 있다. 방정식을 무차원화하기 위해 특성 길이 과 특성 속도 을 정의해야 한다. 이는 무차원 변수가 모두 1차수가 되도록 선택해야 한다. 따라서 다음과 같은 무차원 변수를 얻는다.

:

\rho^*\equiv \frac \rho {\rho_0}, \quad u^*\equiv \frac u {u_0}, \quad r^*\equiv \frac r {r_0}, \quad t^*\equiv \frac {u_0}{r_0} t, \quad \nabla^*\equiv r_0 \nabla , \quad \mathbf g^* \equiv \frac {\mathbf g} {g_0}, \quad \boldsymbol \sigma^* \equiv \frac {\boldsymbol \sigma} {p_0},

이러한 역 관계를 오일러 운동량 방정식에 대입하고, 프루드 수(Fr^영어)를 다음과 같이 정의한다.

:

\mathrm{Fr}=\frac{u_0}{\sqrt{g_0 r_0}},

프루드 수는 다음과 같이 정의된다.

:

Fr=\frac{U}{\sqrt{Lg}}

''U'' : 특성 속도 [m/s]
''L'' : 특성 길이 (선박의 경우 수선장^[6]) [m]
''g'' : 중력 가속도 크기 [m/s²]

3. 역사

개수로 흐름에서, 1828년 장바티스트 벨랑제는 최초로 유속과 중력 가속도에 흐름 깊이를 곱한 값의 제곱근의 비를 도입했다. 이 비율이 1보다 작으면 하천 흐름처럼, 1보다 크면 급류 흐름처럼 작동했다.^[1]

부유 물체의 저항을 정량화한 것은 일반적으로 윌리엄 프루드의 공로로 여겨지는데, 그는 일련의 축척 모형을 사용하여 각 모형이 주어진 속도로 예인될 때 제공하는 저항을 측정했다. 해군 기술자 프레데릭 리치는 1852년에 배와 프로펠러를 테스트하기 위해 훨씬 이전에 이 개념을 제시했지만, 프루드는 이를 알지 못했다.^[2] 프루드는 1868년 '비교 법칙'에서 속도-길이 비율을 다음과 같은 차원적 용어로 정의했다.

: $\text{속도-길이 비율} =\frac{u}{\sqrt {\text{LWL}} }$

여기서:

''u'' = 유속
LWL = 수선 길이

이 용어는 무차원 용어로 변환되었고, 그가 수행한 작업에 대한 인정으로 프루드의 이름을 따서 명명되었다. 프랑스에서는 때때로 프레데릭 리치의 이름을 따서 '''리치-프루드 수'''라고 불린다.^[3]

4. 상류, 사류, 한계류

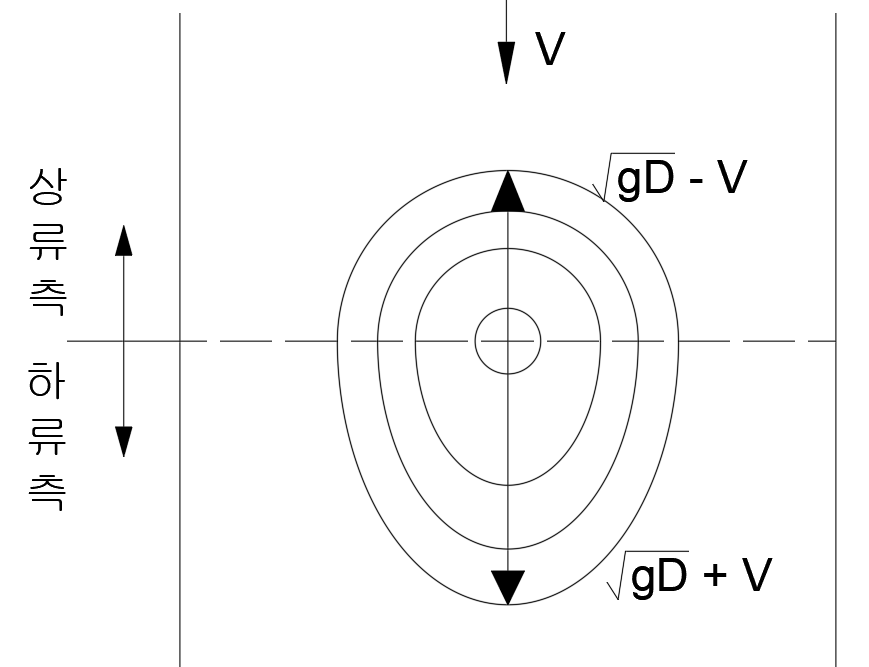
개수로 흐름에서 프루드 수는 흐름의 특성을 나타내는 중요한 지표이다. 프루드 수에 따라 흐름은 상류, 사류, 한계류로 구분된다.

물이 흐르는 수로에 돌멩이를 던지면 수면에 파동이 생긴다. 파동의 속도는 '''표면장파속도'''라고 하며,

\sqrt{gD}

와 같다. 수로 유속에 따라 파동이 전달되는 양상이 달라지는데, 유속이 느릴수록 파동은 상류와 하류 양방향으로 잘 전파된다. 이러한 흐름을 '''상류'''라고 한다. 반면 유속이 빨라지면 상류로 가는 파동은 어느 순간 사라지고 하류로만 파동이 전달되는데, 이때의 흐름을 '''한계류'''라고 한다. 한계류보다 유속이 더 빠르면 파동은 하류로만 빠르게 퍼지며, 이때의 흐름을 '''사류'''라고 한다.

프루드 수는 다양한 크기와 모양의 물체 간의 조파 저항을 비교하는 데 사용된다. 자유 표면 흐름에서 흐름의 성질(초임계 또는 아임계)은 프루드 수가 1보다 큰지 작은지에 따라 달라진다.

주방이나 욕실 싱크대에서 "임계" 흐름의 선을 쉽게 볼 수 있다. 수도꼭지를 틀어 물줄기가 싱크대에 부딪히는 지점 근처에서는 흐름이 초임계 흐름(사류)이다. 물은 표면에 '밀착'되어 빠르게 움직인다. 흐름 패턴의 바깥쪽 가장자리에서는 흐름이 아임계 흐름(상류)이다. 이 흐름은 더 두껍고 더 느리게 움직인다. 두 영역 사이의 경계는 "수력 점프"라고 하며, 흐름이 임계점에 도달하고 프루드 수가 1.0과 같아지는 지점에서 시작된다.

프루드 수는 동물의 보행 패턴 연구에도 활용된다. 동물들이 다양한 보행 패턴을 사용하는 이유를 이해하고, 멸종된 종의 보행에 대한 가설을 세우는 데 도움을 준다. 또한 입자 베드 거동은 최적의 작동 범위를 설정하기 위해 프루드 수(Fr)로 정량화할 수 있다.

4. 1. 상류 (Subcritical flow)

물이 흐르는 수로에 돌멩이를 던지면 수면에 파동이 생긴다. 파동의 속도는 '''표면장파속도'''라고 하며,

\sqrt{gD}

와 같다. 이 파동은 수로 유속이 느릴수록 상류와 하류 양방향으로 잘 전파된다. 이때의 흐름을 '''상류'''라고 한다.

상류인 경우, 상류측으로 전파되는 파의 속도는 표면장파속도

\sqrt{gD}

에서 반대방향으로 흐르는 물의 유속 V를 뺀 값과 같다. 이 값이 양이어야 상류측으로 파동이 전달된다. 즉,

:

\sqrt{gD} - V > 0

:

\sqrt{gD} > V

:

1 > \frac{V}{\sqrt{gD}} = Fr

따라서 상류라면 프루드 수가 1보다 작다.

4. 2. 사류 (Supercritical flow)

사류(Supercritical flow^영어)는 프루드 수 (Fr)가 1보다 큰 흐름으로, 수면파가 하류로만 전파되는 현상이다. 유속이 빠르고 수심이 얕은 급류에서 나타나며, Fr > 1 로 표현한다.^[1]

사류는 다음의 수식으로 정리할 수 있다.^[1]

\sqrt{gD} - V < 0

\sqrt{gD} < V

1 < \frac{V}{\sqrt{gD}} = Fr

V: 유속
g: 중력 가속도
D: 수심
Fr: 프루드 수

4. 3. 한계류 (Critical flow)

물이 흐르는 수로에 돌멩이를 던지면 수면에 파동이 생긴다. 파동의 속도는 '''표면장파속도'''라고 하며, √gD^영어와 같다. 수로 유속이 느리면 파동은 상류와 하류 양쪽으로 잘 퍼진다. 이때의 흐름을 '''상류'''라고 한다. 반면 수로 유속이 빨라지면 상류로 가는 파동은 어느 순간 사라지고, 하류로만 파동이 전달된다. 이때의 흐름을 '''한계류'''라고 한다. 한계류일 때보다 유속이 빠르면 파동은 하류로만 빠르게 퍼지는데, 이때의 흐름을 '''사류'''라고 한다.

한계류는 상류측으로 전파되는 파가 없어지는 순간이므로 표면장파속도와 물의 유속이 같은 순간이다.

:√gD - V = 0^영어

:√gD = V^영어

:1 = V/√gD = Fr^영어

따라서 한계류일 때의 프루드 수는 1이다. 이때 수면파는 정지해 있는 것처럼 보이며, 상류와 사류의 경계가 되는 흐름 상태이다.

5. 다양한 분야에서의 활용

프루드 수는 선박 유체역학, 얕은 물에서의 파동, 풍공학, 지구물리적 질량 흐름, 교반 탱크, 입자 베드 거동, 생체 역학 등 다양한 분야에서 활용된다.

선박 유체역학: 윌리엄 프루드는 선박의 저항을 연구하면서 프루드 수를 정의했으며, 이는 특히 파랑 저항에 중요한 변수이다.
얕은 물에서의 파동: 쓰나미나 수력 점프와 같은 얕은 물에서의 파동 연구에 사용되며, 흐름의 상태(아임계 흐름, 초임계 흐름, 임계 흐름)를 구분한다.
풍공학: 현수교와 같이 바람의 영향을 받는 구조물의 안정성 평가에 사용되어 바람의 변동하는 힘과 구조물의 진동을 분석한다.^[1]
지구물리적 질량 흐름: 눈사태나 토석류와 같은 현상 연구에 확장된 프루드 수를 사용하여 운동 에너지와 위치 에너지의 비율을 나타낸다.
교반 탱크 및 분말 혼합기: 표면 와류 형성을 지배하고, 입자층 유동화 여부를 결정하여 혼합 효율을 예측한다.^[5]
입자 베드 거동: 입자 베드의 최적 작동 범위를 설정하는 데 활용된다.^[3]
생체 역학: 동물의 보행 패턴, 속도, 보행 간 전환 등을 연구하며, 생장비율학에서 사슴^[3], 공룡^[4]을 포함한 육상 동물의 육상 운동 연구에 활용된다.^[2]

5. 1. 선박 유체역학

해양 유체역학에서 프루드 수^영어는 보통 ''Fn''으로 표기하며, 다음과 같이 정의된다.^[3]

:

\mathrm{Fn}_L = \frac{u}{\sqrt{gL}}

여기서 ''u''는 해상과 선박 사이의 상대 유속, ''g''는 중력 가속도, ''L''은 수선 수준에서의 선박 길이를 의미한다. 프루드 수는 특히 파랑 저항 측면에서 선박의 저항에 중요한 변수이다.^[3]

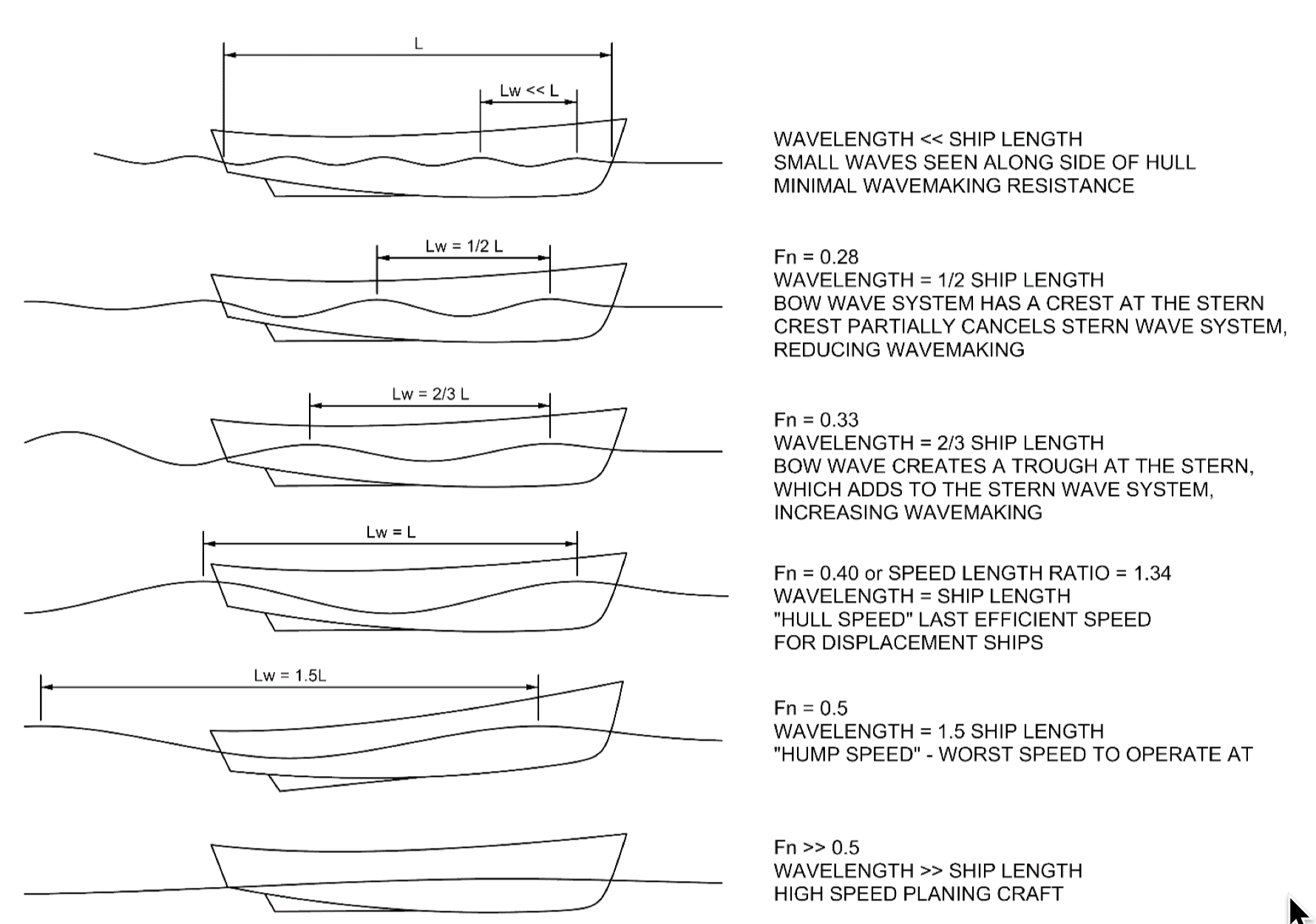
부유 물체의 저항을 정량화한 것은 윌리엄 프루드의 공로로 여겨진다. 그는 일련의 축척 모형을 사용하여 각 모형이 주어진 속도로 예인될 때 제공하는 저항을 측정했다. 원래 속도-길이 비율은 프루드가 1868년 그의 '비교 법칙'에서 다음과 같은 차원적 용어로 정의했다.

:

\text{속도-길이 비율} =\frac{u}{\sqrt {\text{LWL}} }

:여기서:

:* ''u'' = 유속

:* LWL = 수선 길이

이후 이 용어는 무차원 용어로 변환되었고, 그가 수행한 작업에 대한 인정으로 프루드 수로 명명되었다.

활주선과 같이 수선 길이가 속도에 따라 크게 변하는 경우에는 배수량 프루드 수를 사용하는 것이 좋다.

:

\mathrm{Fn}_V = \frac{u}{\sqrt{g\sqrt[3]{V}}}.

5. 2. 얕은 물에서의 파동

쓰나미와 수력 점프와 같이 얕은 물에서 발생하는 파동의 경우, 특성 속도 ''U''는 흐름 방향에 수직인 단면적에 대해 평균화된 평균 유속이다. 파동 속도, 즉 속도 ''c''는 중력 가속도 ''g''에 단면적 ''A''를 곱한 값을 자유 표면 폭 ''B''로 나눈 값의 제곱근과 같다.

따라서 얕은 물에서의 프루드 수는 다음과 같다.

:

\mathrm{Fr} = \frac{U}{\sqrt{g \dfrac{A}{B}}}.

균일한 깊이 ''d''를 가진 직사각형 단면의 경우, 프루드 수는 다음과 같이 단순화될 수 있다.

:

\mathrm{Fr} = \frac{U}{\sqrt{gd}}.

Fr < 1 인 경우 흐름은 아임계 흐름이라고 하며, Fr > 1 인 경우 흐름은 초임계 흐름으로 특징지어진다. Fr ≈ 1 일 때 흐름은 '''임계 흐름'''으로 표시된다.

5. 3. 풍공학

현수교와 같이 바람의 영향을 받는 구조물에 대한 풍력의 영향을 고려할 때, 구조물의 진동과 바람의 변동하는 힘을 함께 고려해야 한다. 이러한 경우 프루드 수를 고려해야 한다.^[1] 뜨거운 연기 기둥과 자연풍을 결합하여 모의 실험할 때도 부력과 바람의 운동량 사이의 균형을 위해 프루드 수 척도가 필요하다.^[1]

5. 4. 지구물리적 질량 흐름

눈사태 및 토석류와 같은 지구물리적 질량 흐름은 경사면에서 발생하여 완만하고 평평한 유출 구역으로 합쳐진다.^[1]

따라서 이러한 흐름은 지형 경사의 고도와 관련된 중력 위치 에너지 및 흐름 중 압력 위치 에너지와 관련이 있다. 그러므로 고전적인 프루드 수는 이러한 추가 효과를 포함해야 하며, 이 경우 프루드 수를 재정의해야 한다. 확장된 프루드 수는 운동 에너지와 위치 에너지의 비율로 정의된다.

:

\mathrm{Fr} = \frac{u}{\sqrt{\beta h + s_g \left(x_d - x\right)}}

x_d

는 질량 방출 지점에서 채널을 따라 흐름이 수평 기준면에 도달하는 지점까지의 거리이다. E_pot^p = βh|E_pot^p = βh^영어 및 E_pot^g = s_g(x_d − x)|E_pot^g = s_g(x_d − x)^영어는 각각 압력 위치 에너지와 중력 위치 에너지이다. 얕은 물 또는 입자 흐름 프루드 수의 고전적인 정의에서는 표면 고도와 관련된 위치 에너지인 E_pot^g|E_pot^g^영어는 고려되지 않는다. 확장된 프루드 수는 표면 고도가 높을수록 고전적인 프루드 수와 실질적으로 다르다. 항 βh|βh^영어는 경사면을 따라 이동하는 질량의 형상 변화로부터 나타난다. 차원 분석에 따르면 얕은 흐름의 경우 βh ≪ 1|βh ≪ 1^영어인 반면, u|u^영어와 s_g(x_d − x)|s_g(x_d − x)^영어는 모두 1과 같다. 질량이 사실상 침상 면에 평행한 자유 표면을 가진 얕은 경우, βh|βh^영어는 무시할 수 있다. 이러한 상황에서 중력 위치 에너지를 고려하지 않으면 운동 에너지가 제한되어 있어도 Fr|Fr^영어은 무한대가 된다. 따라서 중력 위치 에너지로 인한 추가 기여를 공식적으로 고려하면 Fr의 특이점이 제거된다.

5. 5. 교반 탱크

교반 탱크에서 프루드 수는 표면 와류의 형성을 지배한다. 임펠러 팁 속도는 circular motion|원운동^영어이며, 여기서 ω는 임펠러 주파수(rpm)이고 r은 임펠러 반경이다. 따라서 프루드 수는 다음과 같은 형태를 갖는다.^[5]

:

\mathrm{Fr}=\omega \sqrt \frac{r}{g}.

프루드 수는 분말 혼합기에서도 유사하게 적용된다. Fr<1이면 입자가 단순히 교반되지만, Fr>1이면 분말에 가해지는 원심력이 중력을 압도하여 입자층이 유동화되어 혼합을 촉진한다.^[5]

5. 6. 입자 베드 거동

입자 베드의 거동은 프루드 수(Fr)로 정량화할 수 있으며, 최적의 작동 범위를 설정하는 데 사용된다.^[3]

5. 7. 생체 역학

프루드 수는 생장비율학에서 사슴과^[3] 공룡을 포함한^[4] 육상 동물의 육상 운동 연구에 적용되어 왔다.^[2]

프루드 수는 동물의 보행 패턴 경향을 연구하는 데 사용될 수 있다. 다리 보행 운동 역학 분석에서 보행하는 다리는 종종 발을 중심으로 하는 원형 호를 통과하는 질량 중심을 가진 역진자로 모델링된다. 프루드 수는 움직임의 중심인 발을 중심으로 하는 구심력과 보행하는 동물의 중력 비율이다.

Fr^영어 = 구심력^영어 / 중력^영어 = (mv²/l) / mg = v²/gl

여기서 ''m''은 질량, ''l''은 특성 길이, ''g''는 중력 가속도, ''v''는 속도이다. 특성 길이 ''l''은 연구에 맞게 선택될 수 있다. 예를 들어, 일부 연구에서는 엉덩이 관절에서 지면까지의 수직 거리를 사용했으며, 다른 연구에서는 전체 다리 길이를 사용했다.

프루드 수는 다음과 같이 보폭 빈도 ''f''로부터 계산될 수도 있다.

Fr^영어 = v²/gl = (lf)²/gl = lf²/g

전체 다리 길이가 특성 길이로 사용되면 보행의 이론적 최대 속도는 프루드 수가 1.0이다. 이는 더 높은 값이면 이륙하여 발이 땅에 닿지 않기 때문이다. 두 발 보행에서 달리기로의 일반적인 전환 속도는 Fr^영어 ≈ 0.5 에서 발생한다. R. M. 알렉산더는 크기와 질량이 다르지만 동일한 프루드 수를 가진 동물들이 일관되게 유사한 보행을 보인다는 것을 발견했다. 이 연구는 동물들이 일반적으로 프루드 수 1.0 근처에서 아블에서 대칭적인 달리기 보행 (예: 속보 또는 평보)으로 전환한다는 것을 발견했다. 비대칭 보행 (예: 캔터, 가로 갤럽, 회전 갤럽, 바운드 또는 프로크)에 대한 선호도는 프루드 수 2.0과 3.0 사이에서 관찰되었다.

6. 무차원화된 나비에-스토크스 방정식

중력이 작용하는 비압축성 점성 흐름의 나비에-스토크스 방정식은 다음 식으로 주어진다.^[7]

: $\frac{ \partial \boldsymbol{v} }{ \partial t } + ( \boldsymbol{v} \cdot \nabla )\boldsymbol{v} = -\frac{ 1 }{ \rho } \nabla p + \nu \nabla^2 \boldsymbol{v} + g\boldsymbol{e}_g$

여기서 '''e'''_g는 중력 방향(수직 아래)을 향하는 단위 벡터이다.

이 식을 무차원화하면^[7]

: $\frac{ \partial \boldsymbol{v} }{ \partial t } + ( \boldsymbol{v} \cdot \nabla )\boldsymbol{v} = -\nabla p + \frac{1}{Re} \nabla^2 \boldsymbol{v} + \frac{1}{Fr^2}\boldsymbol{e}_g$

가 되어, 이 흐름은 레이놀즈 수 ''Re''와 프루드 수 ''Fr''에 의해서만 특징지어짐을 알 수 있다.

조파 저항을 다루는 경우 ''Re''는 충분히 크고, 흐름의 양상이 ''Re''에 거의 의존하지 않으므로, 흐름은 프루드 수 ''Fr''에 의해서만 결정된다.

7. 한국의 관점

프루드 수에 대한 한국의 관점을 나타내는 자료가 제공되지 않았기 때문에, 해당 섹션을 작성할 수 없습니다.

참조

_[1] 웹사이트 James Anthony Froude http://www.merriam-w[...]
_[2] 서적 Functional Vertebrate Morphology Harvard University Press 2013-10-01
_[3] 논문 Allometry of the limbs of antelopes (Bovidae) https://onlinelibrar[...] 1977
_[4] 논문 How Dinosaurs Ran https://www.jstor.or[...] 1991
_[5] 웹사이트 Powder Mixing - Powder Mixers Design - Ribbon blender, Paddle mixer, Drum blender, Froude Number https://www.powderpr[...] 2019-05-31
_[6] 서적 ハイテク兵器の物理学（財）防衛技術協会編 2006-03
_[7] 문서 無次元化された各変数を、もとの有次元変数と同じ記号を用いて表しているので注意。無次元化の過程については[[レイノルズ数#ナビエ-ストークス方程式]]を参照のこと。
_[8] 문서 수로 횡단면에서 수표면 부분의 길이

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com