휨

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

휨은 구조물이 하중을 받아 구부러지는 현상을 의미하며, 순수 휨, 보의 준정적 휨, 탄성 지반 위의 보, 보의 동적 휨, 판의 준정적 휨, 판의 동적 휨 등 다양한 형태로 나타난다. 순수 휨은 균일한 굽힘 모멘트만 받는 상태를 말하며, 보의 곡률, 소성 휨, 복잡하거나 비대칭 휨, 큰 휨 변형, 티모셴코 휨 이론 등 다양한 이론으로 분석된다. 탄성 지반 위의 보는 철도, 건물 기초 등에 적용되며, 오일러-베르누이 이론과 티모셴코-레일리 이론으로 분석된다. 보의 동적 휨은 굽힘 진동으로, 오일러-베르누이 이론과 티모셴코-레일리 이론으로 설명된다. 판의 준정적 휨은 키르히호프-러브 판 이론과 민들린-레이스너 판 이론으로, 판의 동적 휨은 판 이론을 통해 분석된다.

더 읽어볼만한 페이지

정역학 - 수직항력
수직항력은 물체가 표면에 놓였을 때 표면이 물체에 가하는 힘으로, 중력에 대항하여 물체가 가라앉는 것을 막으며, 파울리 배타 원리에 의해 발생하고, 엘리베이터나 놀이기구와 같은 실생활 상황에서 나타난다.
정역학 - 정적 평형 상태
정적 평형 상태는 물리학에서 물체에 작용하는 모든 힘과 모멘트의 합이 0이 되어 움직이지 않고 안정된 상태를 유지하는 기계적 평형의 특수한 경우를 의미한다.
재료역학 - 비등방성
비등방성은 재료의 미세구조, 결정구조, 분자 배열 등으로 인해 물질의 물리적, 화학적 성질이 방향에 따라 달라지는 현상으로, 다양한 분야에서 중요한 역할을 하며 측정 및 분석을 통해 재료 설계 및 응용에 활용된다.
재료역학 - 비틀림
비틀림은 물체에 동일하고 반대 방향의 힘이 작용하여 꼬이는 현상으로, 구조 부재에 비틀림 모멘트가 작용할 때 발생하며, 전단 응력을 유발하고, 비틀림 상수, 전단 응력, 비틀림 각도 등으로 분석되며 샤프트 설계에 중요하다.
구조공학 - 프리스트레스트 콘크리트
프리스트레스트 콘크리트는 철근 콘크리트의 단점을 보완하고자 콘크리트에 미리 압축 응력을 가하여 인장 응력을 상쇄하거나 감소시킨 콘크리트 구조이며, 고강도 강재와 콘크리트를 사용하여 내구성을 향상시키고 교량, 건축물 등 다양한 분야에 적용된다.
구조공학 - 모노코크
모노코크는 외부 껍데기가 주요 하중을 지지하는 구조로, 넓은 내부 공간과 경량화를 가능하게 하여 항공기, 자동차, 철도 차량 등 다양한 분야에 적용되었으나, 현재는 세미 모노코크 구조나 특수 목적 차량에 주로 사용된다.

휨

2. 순수 휨

보가 균일한 모멘트만을 받는 상태를 '''순수 휨'''이라고 한다. 순수 휨 상태에서 보 내부에 발생하는 수직응력은 다음 공식으로 계산된다.^[1]

: $\sigma = -\frac{My}{I_x}$

M: 단면이 받는 휨 모멘트
I_x: 중립축에 대한 단면이차모멘트
y: 단면 중립축에서 응력을 구하고자 하는 위치까지의 수직 거리

폭이 b, 높이가 h인 직사각형 단면의 단면이차모멘트는

I = \frac{bh^3}{12}

이므로, 수직응력은 다음과 같이 간단하게 표현할 수 있다.^[1]

:

\sigma = \frac{6M}{bh^2}

2. 1. 보의 곡률

보에 순수 휨이 작용하는 경우

\rho

은

\rho=\frac{EI}{M}=R

이다. 곡률은 곡률 반경의 역수로,

\frac{1}{R}=\frac{M}{EI}

이다.

3. 보의 준정적 휨

보에 가로 하중이 가해지면 보가 변형되고 내부에 응력이 발생한다. 준정적 휨의 경우, 처짐의 양과 발생하는 응력은 시간에 따라 변하지 않는다고 가정한다. 양쪽 끝이 지지되고 중간에 하향 하중이 가해지는 수평 보에서, 보의 위쪽 면은 압축되고 아래쪽 면은 늘어난다.^[1]

가로 하중에 의해 발생하는 내부 응력에는 두 가지 형태가 있다.^[1]

가로 하중에 평행한 전단 응력과 하중 방향에 수직인 평면에서 발생하는 보완적인 전단 응력
보의 윗부분에 작용하는 압축 응력(주로 시멘트 콘크리트 요소에 적용)과 보의 아랫부분에 작용하는 인장 응력(강철 요소에 적용)

이 두 힘은 크기가 같고 방향이 반대이므로 모멘트를 형성하며, 이 굽힘 모멘트는 보의 처짐 변형에 저항한다. 몇 가지 단순화된 가정을 사용하면 보의 응력 분포를 매우 정확하게 예측할 수 있다.^[1]

3. 1. 오일러-베르누이 휨 이론

굽힘 빔의 요소: 섬유는 동심원을 형성하고, 상단 섬유는 압축되고 하단 섬유는 늘어납니다.

오일러-베르누이 휨 이론은 가늘고 긴 보의 휨을 설명하는 이론이다. 주요 가정은 '평면 단면은 평면으로 유지된다'는 것으로, 단면을 가로지르는 전단으로 인한 변형은 고려하지 않는다(전단 변형 없음). 이 선형 분포는 최대 응력이 재료의 항복 강도보다 작은 경우에만 적용된다.^[1]

이 이론에서는 다음과 같은 조건이 참인 보를 고려한다.

보는 원래 직선이고 가늘며, 테이퍼는 약간 있다.
재료는 등방성(또는 직교이방성 재료)이고, 선형 탄성이며, 모든 단면에서 균질하다(그러나 반드시 길이를 따라 균질할 필요는 없음).
작은 처짐만 고려된다.

이 경우, 보 처짐(

w

)을 설명하는 방정식은 다음과 같이 근사될 수 있다.

:

\cfrac{\mathrm{d}^2 w(x)}{\mathrm{d} x^2}=\frac{M(x)}{E(x) I(x)}

여기서

x

에 대한 처짐 형상의 2차 미분은 곡률로 해석되고,

E

는 영률,

I

는 단면의 단면 2차 모멘트,

M

은 보 내부의 굽힘 모멘트이다.

보가 길이를 따라 균질하고 테이퍼가 없으며(즉, 일정한 단면) 가해진 횡방향 하중

q(x)

에서 처짐이 발생하면 다음과 같이 나타낼 수 있다.^[1]

:

EI~\cfrac{\mathrm{d}^4 w(x)}{\mathrm{d} x^4} = q(x)

이것은 보 굽힘에 대한 오일러-베르누이 방정식이다.

보의 변위에 대한 해를 얻은 후, 보의 굽힘 모멘트(

M

) 및 전단력(

Q

)은 다음 관계를 사용하여 계산할 수 있다.

:

M(x) = -EI~\cfrac{\mathrm{d}^2 w}{\mathrm{d} x^2} ~;~~ Q(x) = \cfrac{\mathrm{d}M}{\mathrm{d}x}.

단순 보 굽힘은 종종 오일러-베르누이 보 방정식으로 분석된다. 단순 굽힘 이론을 사용하기 위한 추가적인 조건은 다음과 같다.^[4]

# 보는 순수 굽힘을 받는다. 즉, 전단력이 0이고 비틀림 또는 축 방향 하중이 없다.

# 보의 단면은 굽힘 동안 평면으로 유지된다.

굽힘 하중 하에서 보 축의 방향으로 압축력과 인장력이 발생한다. 이러한 힘은 보에 응력을 유발한다. 최대 압축 응력은 보의 최상단 가장자리에서, 최대 인장 응력은 보의 하단 가장자리에서 발견된다. 이 두 최대값 사이의 응력은 선형적으로 변하므로, 굽힘 응력이 없는 중립축이 존재한다.

단순 굽힘에서 보의 굽힘 응력을 결정하기 위한 고전적인 공식은 다음과 같다.^[5]

:

\sigma_x = \frac{M_z y}{I_z} = \frac{M_z}{W_z}

여기서

${\sigma_x}$ 는 굽힘 응력이다.
$M_z$ – 중립축에 대한 모멘트
$y$ – 중립축에 대한 수직 거리
$I_z$ – 중립축 ''z''에 대한 단면 2차 모멘트.
$W_z$ - 중립축 ''z''에 대한 저항 모멘트. $W_z = I_z / y$

3. 1. 1. 소성 휨

보의 응력이 항복 강도를 초과하면 소성 굽힘이 발생한다. 이때, 연성 재료는 '소성 힌지' 상태가 되는데, 빔 전체에서 응력의 크기가 항복 응력과 같아진다. 응력은 인장에서 압축으로 변하는 중립 축에서 불연속성을 보인다. 이러한 소성 힌지 상태는 강철 구조물 설계에서 극한 상태로 활용된다.^[5]

3. 1. 2. 복잡하거나 비대칭 휨

단면이 대칭이 아닌 보에서 발생하는 복잡한 휨 응력을 계산하는 방법을 설명한다. 이러한 휨의 경우, 빔 단면의 임의의 점에서 휨 응력을 계산하기 위해 다음 방정식을 사용한다.^[6]

:

\sigma_x(y,z) = - \frac {M_z~I_y + M_y~I_{yz}} {I_y~I_z - I_{yz}^2}y + \frac {M_y~I_z + M_z~I_{yz}} {I_y~I_z - I_{yz}^2}z

여기서 각 변수는 다음과 같다.

$y,z$ : 응력을 결정해야 하는 단면의 한 점의 좌표
$M_y$ , $M_z$ : y 및 z 도심 축에 대한 굽힘 모멘트
$I_y$ , $I_z$ : y 및 z 축에 대한 단면 2차 모멘트
$I_{yz}$ : 단면적 곱

이 방정식을 사용하면 모멘트 방향이나 단면 형상에 관계없이 빔 단면의 임의의 점에서 휨 응력을 계산할 수 있다.

M_y, M_z, I_y, I_z, I_{yz}

는 단면의 한 점에서 다른 점으로 변하지 않는다.

3. 1. 3. 큰 휨 변형

물체가 크게 변형될 때, 단면의 응력은 다음과 같은 확장된 공식을 사용하여 계산합니다. 우선, 다음 가정이 필요합니다.

# 평면 단면 가정: 변형 전후에 물체의 단면은 평면을 유지합니다. 즉, 회전하지 않습니다.

# 단면의 법선 벡터에 수직인 전단 및 법선 응력은 단면에 평행한 법선 응력에 영향을 주지 않습니다.

큰 굽힘은 굽힘 반경

\rho

가 단면 높이 h의 10배보다 작을 때 고려해야 합니다.

:

\rho < 10 h.

이러한 가정 하에, 큰 굽힘 응력은 다음과 같이 계산됩니다.

:

\sigma = \frac {F} {A} + \frac {M} {\rho A} + {\frac {M} y{\frac {\rho}{\rho +y}}

각 기호는 다음을 의미합니다.

$F$ : 법선 힘
$A$ : 단면 면적
$M$ : 굽힘 모멘트
$\rho$ : 국부 굽힘 반경 (현재 단면에서의 굽힘 반경)
${{I_x}'}$ : $y$ 위치에서 ''x''축에 대한 면적 관성 모멘트 (슈타이너 정리 참조)
$y$ : 응력 $\sigma$ 를 계산하는 단면적의 ''y''축 방향 위치

굽힘 반경

\rho

가 무한대에 가까워지고,

y\ll\rho

인 경우, 원래 공식이 다시 나타납니다.

:

\sigma = {F \over A} \pm \frac {My}{I}

.

3. 2. 티모셴코 휨 이론

티모셴코는 1921년, 오일러-베르누이 보 이론에 전단의 효과를 추가하여 보 이론을 개선했다. 티모셴코 이론에서 보의 축에 수직인 선은 변형 후에도 직선을 유지하지만, 반드시 수직을 유지할 필요는 없다. 또한 보의 두께는 변형 후에도 변하지 않는다고 가정한다.

티모셴코 보의 변형. 수직선은 $\theta$ 만큼 회전하며, 이는 $dw/dx$ 와 같지 않다.

이러한 가정을 바탕으로, 선형 탄성, 등방성, 균질한 균일 단면 보의 굽힘을 나타내는 방정식은 다음과 같다.^[12]

:

EI~\cfrac{\mathrm{d}^4 w}{\mathrm{d} x^4} = q(x) - \cfrac{EI}{k A G}~\cfrac{\mathrm{d}^2 q}{\mathrm{d} x^2}

여기서,

$I$ 는 단면의 단면 2차 모멘트
$A$ 는 단면적
$G$ 는 전단 탄성 계수
$k$ 는 '''전단 보정 계수'''
$q(x)$ 는 가해지는 횡방향 하중
$E$ 는 영률
$w$ 는 보의 처짐

이다. 푸아송 비(

\nu

)가 0.3에 가까운 재료의 경우, 직사각형 단면의 전단 보정 계수는 대략 다음과 같다.

:

k = \cfrac{5 + 5\nu}{6 + 5\nu}

수직선의 회전(

\varphi(x)

)은 다음 방정식으로 표현된다.

:

\cfrac{\mathrm{d}\varphi}{\mathrm{d}x} = -\cfrac{\mathrm{d}^2w}{\mathrm{d}x^2} -\cfrac{q(x)}{kAG}

굽힘 모멘트(

M

)와 전단력(

Q

)은 다음과 같이 계산된다.

:

M(x) = -EI~ \cfrac{\mathrm{d}\varphi}{\mathrm{d}x} ~;~~ Q(x) = kAG\left(\cfrac{\mathrm{d}w}{\mathrm{d}x}-\varphi\right) = -EI~\cfrac{\mathrm{d}^2\varphi}{\mathrm{d}x^2} = \cfrac{\mathrm{d}M}{\mathrm{d}x}

4. 탄성 지반 위의 보

오일러-베르누이, 티모셴코 등 기타 휨 이론에 따르면, 탄성 지반 위의 보를 설명할 수 있다. 철도, 건물 및 기계의 기초, 물 위의 선박, 식물의 뿌리 등과 같은 일부 응용 분야에서 하중을 받는 보는 연속적인 탄성 지반에 의해 지지된다(즉, 외부 하중에 의한 연속적인 반력은 보의 길이를 따라 분포됨).^[7]^[8]^[9]^[10]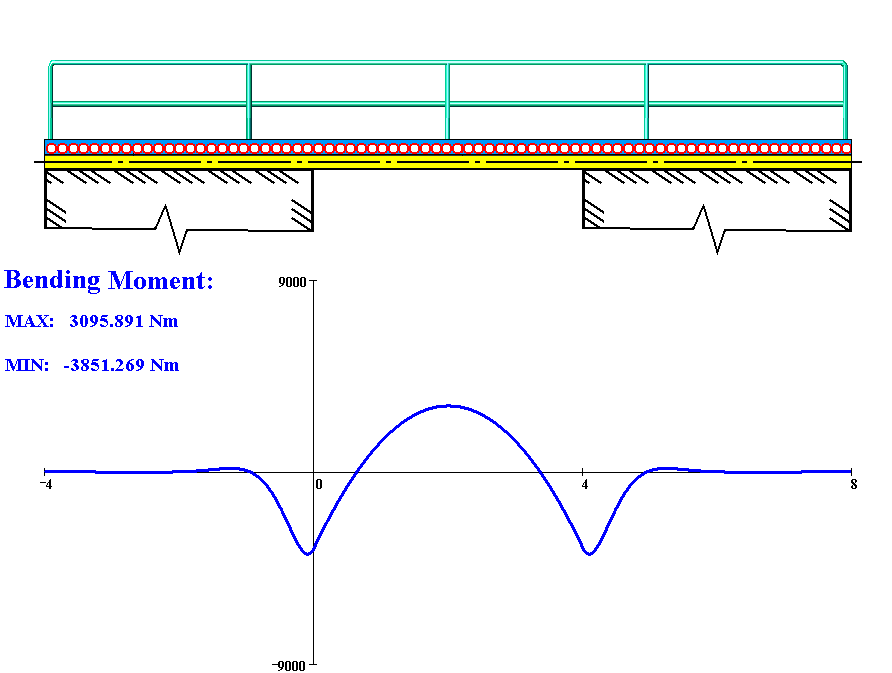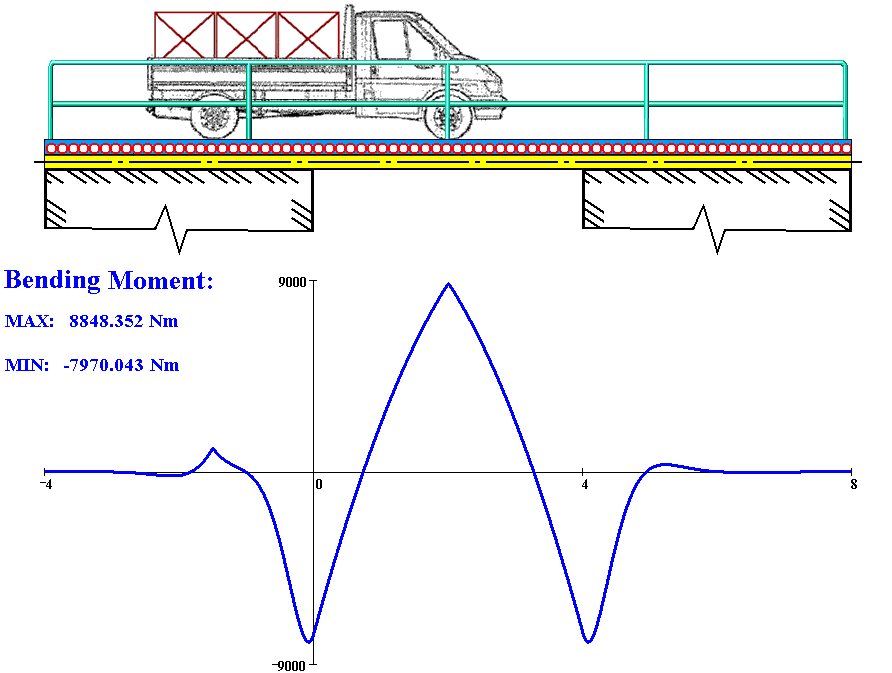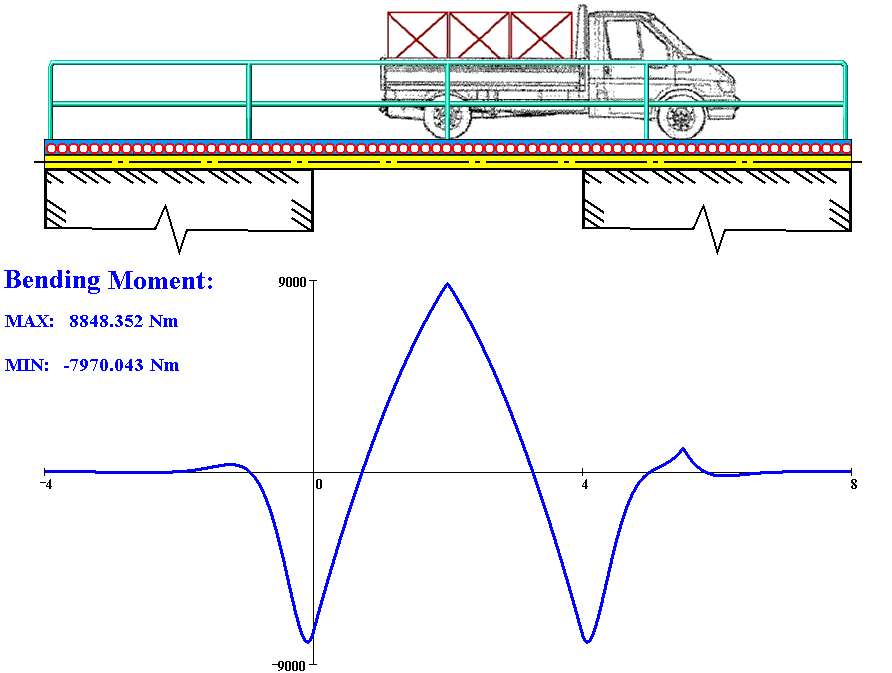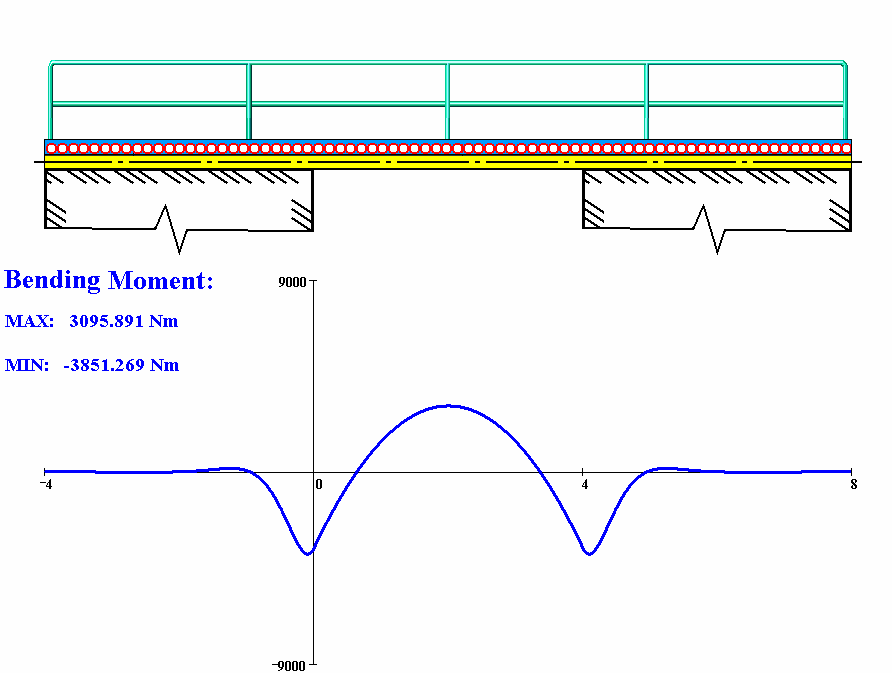

차량이 교량을 건너는 모습 (탄성 지반에 부분적으로 지지된 보, 휨 모멘트 분포)

5. 보의 동적 휨

보의 동적 휨^[11]은 보의 굽힘 진동이라고도 하며, 18세기 말 다니엘 베르누이에 의해 처음 연구되었다. 베르누이의 진동 보에 대한 운동 방정식은 보의 고유 진동수를 과대 평가하는 경향이 있었고, 1877년 레일리가 중간 평면 회전을 추가하여 약간 개선하였다. 1921년 스테판 티모셴코는 굽힘 보의 동적 응답에 대한 전단 효과를 통합하여 이론을 더욱 개선했다. 이를 통해 동적 오일러-베르누이 이론으로는 부적절한 높은 진동수의 문제를 해결하는 데 이론을 사용할 수 있었다. 보의 동적 굽힘에 대한 오일러-베르누이 및 티모셴코 이론은 엔지니어들에 의해 광범위하게 사용되고 있다.

5. 1. 오일러-베르누이 이론

오일러-베르누이 이론은 가늘고 긴 보의 휨을 설명하는 이론이다. 이 이론의 핵심 가정은 '평면 단면은 평면으로 유지된다'는 것으로, 단면을 가로지르는 전단 변형은 고려하지 않는다. 또한, 이 이론은 최대 응력이 재료의 항복 강도보다 작은 경우에만 적용된다.

다음 조건을 만족하는 보를 생각해보자.

보는 원래 직선이고 가늘며, 테이퍼는 약간 있다.
재료는 등방성(또는 직교이방성)이고, 선형 탄성이며, 모든 단면에서 균질하다.
작은 처짐만 고려한다.

이 경우, 보의 처짐(

w

)은 다음 방정식으로 근사할 수 있다.

:

\cfrac{\mathrm{d}^2 w(x)}{\mathrm{d} x^2}=\frac{M(x)}{E(x) I(x)}

여기서

x

에 대한 처짐 형상의 2차 미분은 곡률로 해석되고,

E

는 영률,

I

는 단면의 단면 2차 모멘트,

M

은 보 내부의 굽힘 모멘트이다.

보가 길이를 따라 균질하고, 단면이 일정하며, 가해진 횡방향 하중

q(x)

에서 처짐이 발생하면, 다음과 같이 나타낼 수 있다.^[1]

:

EI~\cfrac{\mathrm{d}^4 w(x)}{\mathrm{d} x^4} = q(x)

이것이 보 굽힘에 대한 오일러-베르누이 방정식이다.

보의 변위에 대한 해를 얻은 후, 보의 굽힘 모멘트(

M

) 및 전단력(

Q

)은 다음 관계를 사용하여 계산할 수 있다.

:

M(x) = -EI~\cfrac{\mathrm{d}^2 w}{\mathrm{d} x^2} ~;~~ Q(x) = \cfrac{\mathrm{d}M}{\mathrm{d}x}.

단순 보 굽힘은 종종 오일러-베르누이 보 방정식으로 분석된다. 단순 굽힘 이론을 사용하기 위한 조건은 다음과 같다.^[4]

# 보는 순수 굽힘을 받는다. 즉, 전단력이 0이고 비틀림 또는 축 방향 하중이 없다.

# 재료는 등방성 (또는 직교이방성)이고 균질하다.

# 재료는 후크의 법칙을 따릅니다(선형 탄성이며 소성 변형이 발생하지 않음).

# 보는 처음에는 직선이며, 보 길이 전체에 걸쳐 단면이 일정하다.

# 보는 굽힘 평면에 대칭축이 있다.

# 보의 비율은 압괴, 주름 또는 측면 좌굴보다 굽힘에 의해 실패하도록 되어 있다.

# 보의 단면은 굽힘 동안 평면으로 유지된다.

굽힘 하중 하에서 보 축의 방향으로 압축력과 인장력이 발생한다. 이러한 힘은 보에 응력을 유발한다. 최대 압축 응력은 보의 최상단 가장자리에서, 최대 인장 응력은 보의 하단 가장자리에서 발견된다. 이 두 응력 사이에는 선형적으로 변하는 지점이 존재하며, 굽힘 응력이 없는 이 점들의 자취는 중립축이다. 균일한 단면의 보를 사용하는 것은 붕괴 직전까지 보의 전체 용량을 사용하지 않기 때문에 하중을 지지하는 효율적인 방법이 아니다. 광폭 플랜지 보(-보s) 및 트러스 거더는 응력이 낮은 영역에서 재료의 양을 최소화하여 이러한 비효율성을 해결한다.

단순 굽힘에서 보의 굽힘 응력을 결정하기 위한 고전적인 공식은 다음과 같다.^[5]

:

\sigma_x = \frac{M_z y}{I_z} = \frac{M_z}{W_z}

여기서

${\sigma_x}$ 는 굽힘 응력이다.
$M_z$ – 중립축에 대한 모멘트
$y$ – 중립축에 대한 수직 거리
$I_z$ – 중립축 ''z''에 대한 단면 2차 모멘트.
$W_z$ - 중립축 ''z''에 대한 저항 모멘트. $W_z = I_z / y$

보의 동적 굽힘^[11]은 보의 굽힘 진동이라고도 하며, 18세기 말 다니엘 베르누이에 의해 처음 연구되었다. 베르누이의 방정식은 보의 고유 진동수를 과대 평가하는 경향이 있었고, 1877년 레일리에 의해, 그리고 1921년 스테판 티모셴코에 의해 개선되었다.

균일한 단면을 갖는 보의 동적 굽힘에 대한 오일러-베르누이 방정식은 다음과 같다.^[12]

:

EI~\cfrac{\partial^4 w}{\partial x^4} + m~\cfrac{\partial^2 w}{\partial t^2} = q(x,t)

여기서

E

는 영률,

I

는 단면의 단면 이차 모멘트,

w(x,t)

는 보의 중립축의 처짐,

m

은 보 단위 길이당 질량이다.

5. 1. 1. 자유 진동

오일러-베르누이 보 방정식에 따르면, 보에 가해지는 횡하중이 없을 때 휨 방정식은 다음과 같이 표현된다.^[12]

:

EI~\cfrac{\partial^4 w}{\partial x^4} + m~\cfrac{\partial^2 w}{\partial t^2} = 0

여기서

E

는 영률,

I

는 단면의 단면 2차 모멘트,

w(x,t)

는 보의 중립축의 처짐,

m

은 보 단위 길이당 질량이다.

보의 자유 조화 진동은 다음과 같이 표현할 수 있다.

:

w(x,t) = \text{Re}[\hat{w}(x)~e^{-i\omega t}] \quad \implies \quad \cfrac{\partial^2 w}{\partial t^2} = -\omega^2~w(x,t)

이를 휨 방정식에 대입하면 다음과 같다.

:

EI~\cfrac{\mathrm{d}^4 \hat{w}}{\mathrm{d}x^4} - m\omega^2\hat{w} = 0

위 방정식의 일반해는 다음과 같다.

:

\hat{w} = A_1\cosh(\beta x) + A_2\sinh(\beta x) + A_3\cos(\beta x) + A_4\sin(\beta x)

여기서

A_1, A_2, A_3, A_4

는 상수이고,

:

\beta := \left(\cfrac{m}{EI}~\omega^2\right)^{1/4}

이며,

\omega

는 고유 진동수를 나타낸다.

캔틸레버 보의 모드 형상
1차 횡방향 굽힘	1차 비틀림	1차 수직 굽힘
2차 횡방향 굽힘	2차 비틀림	2차 수직 굽힘

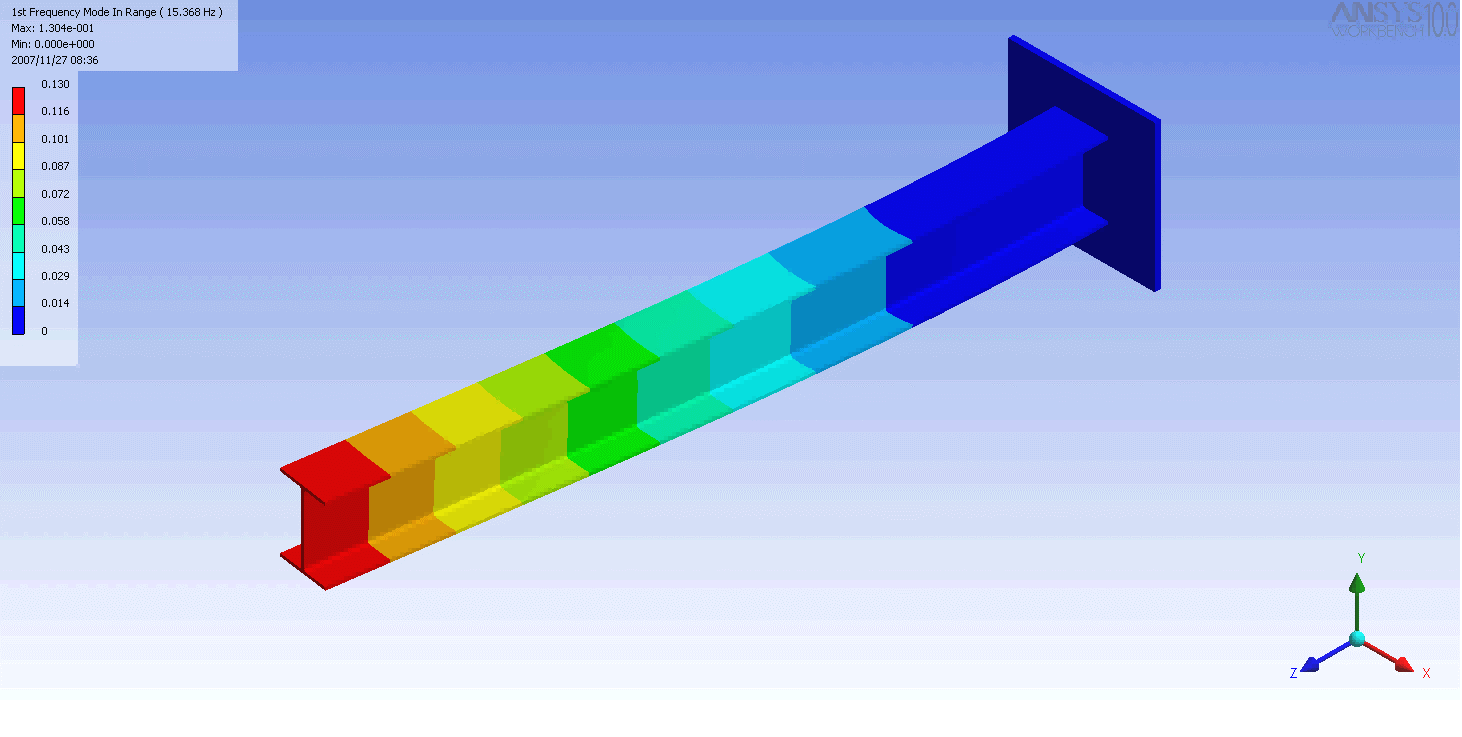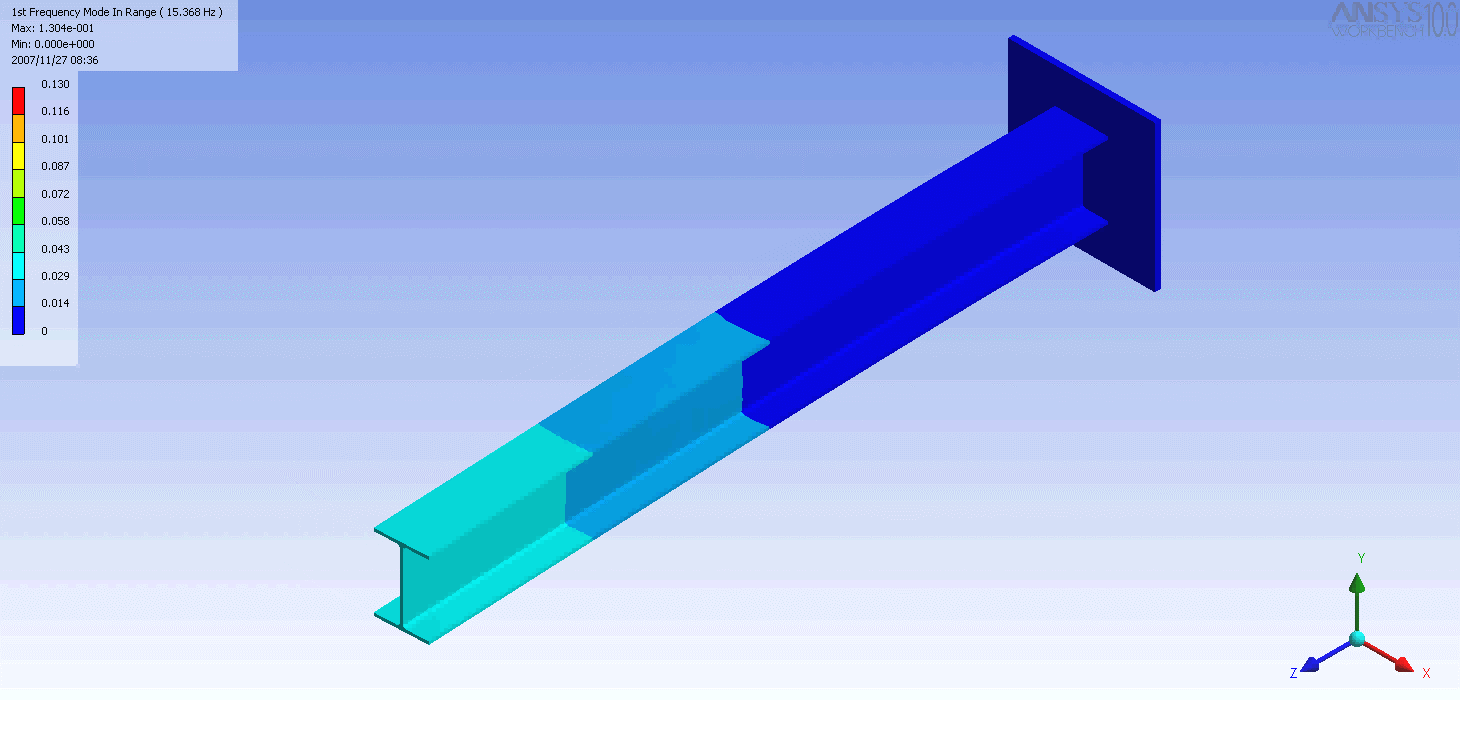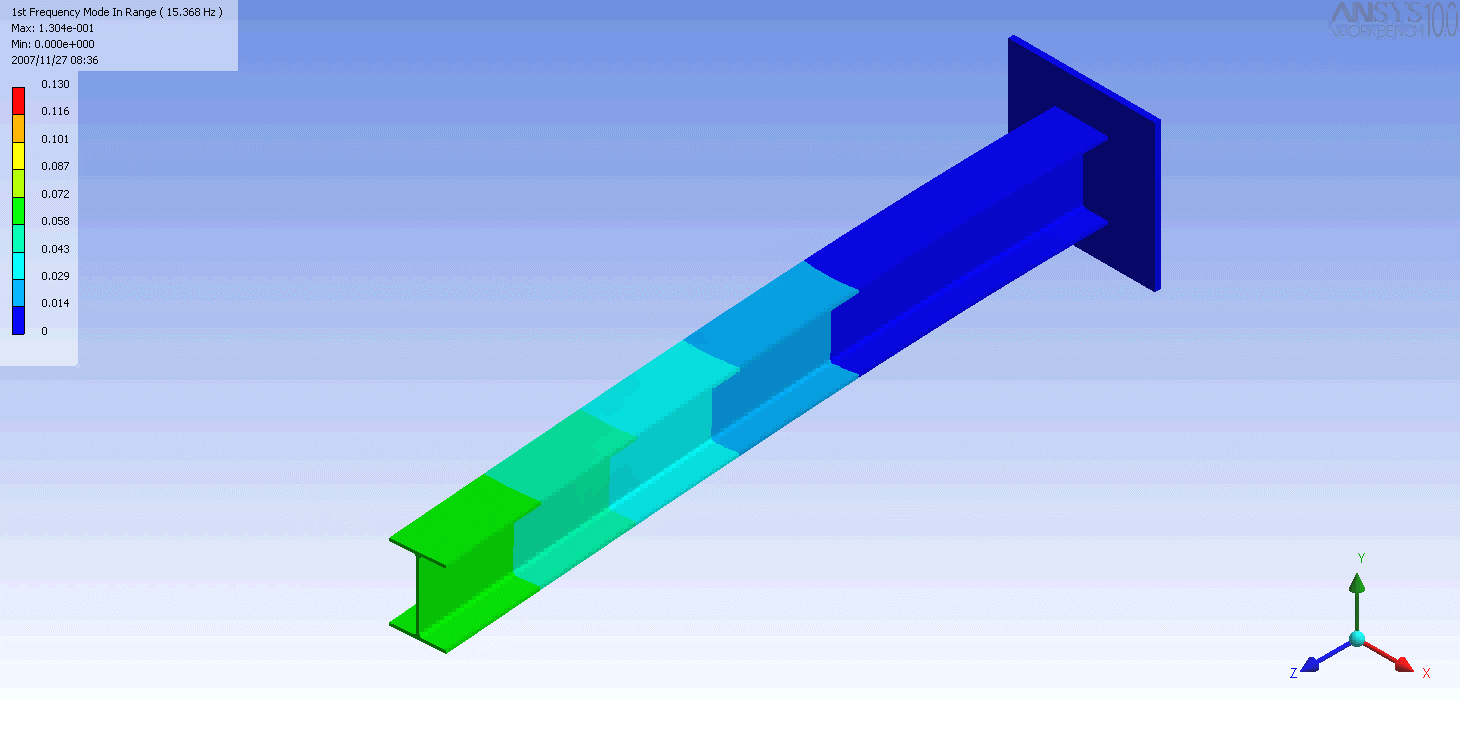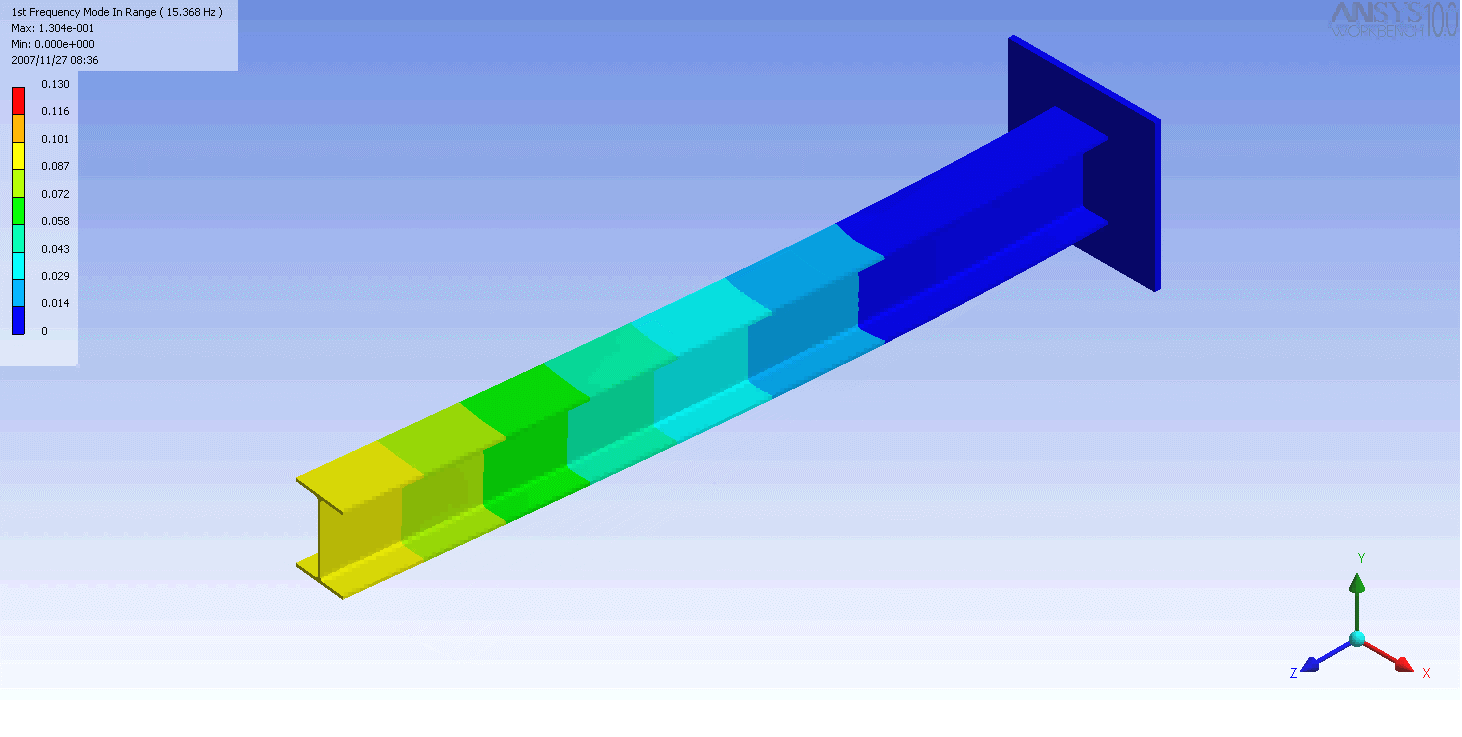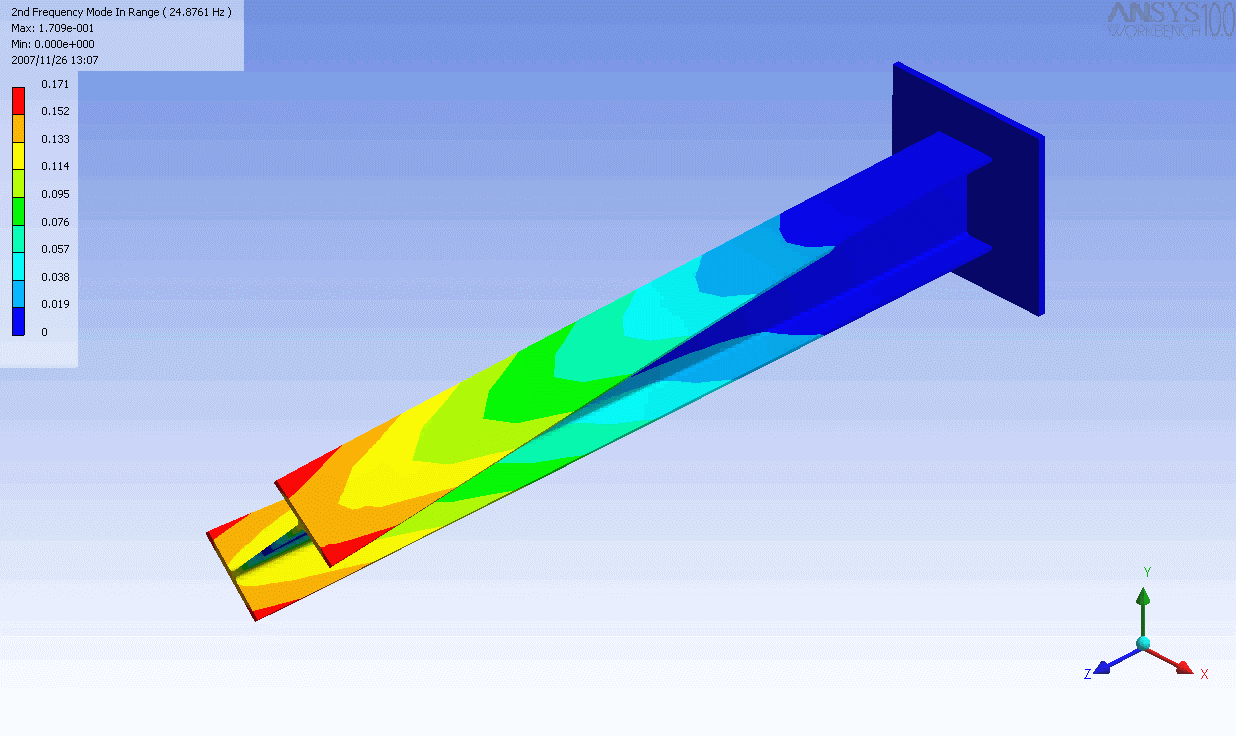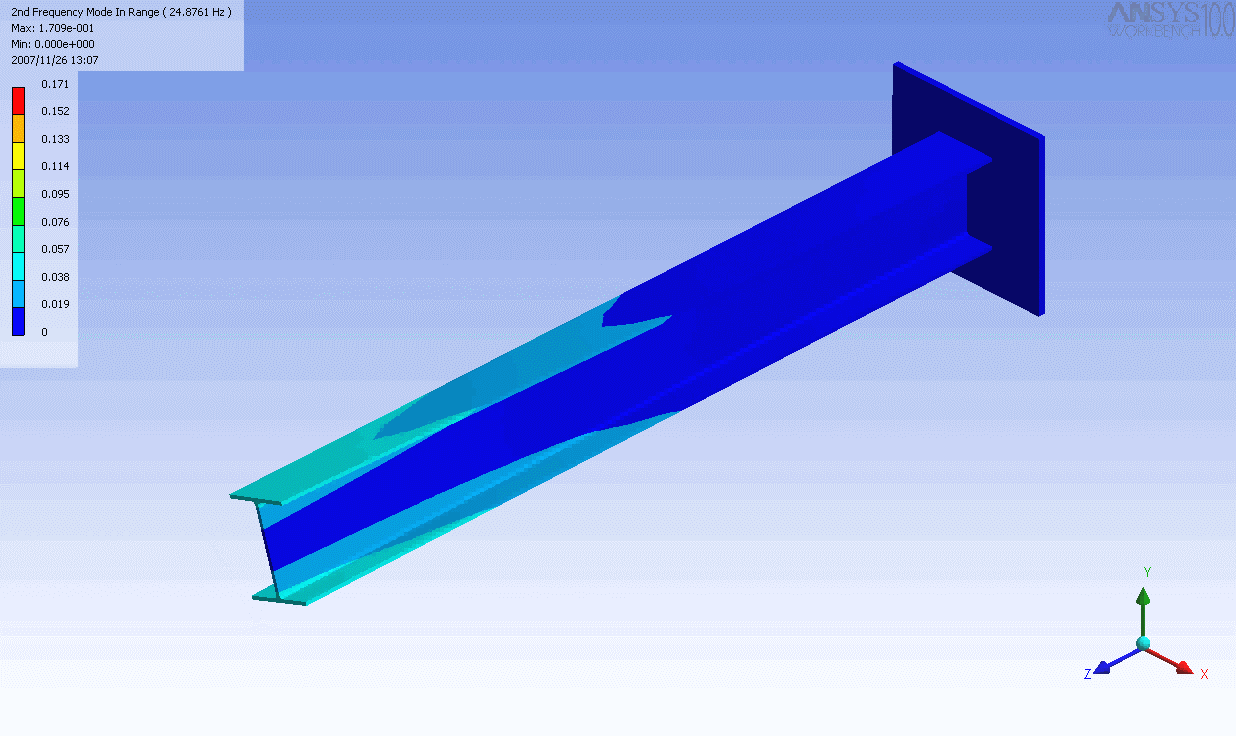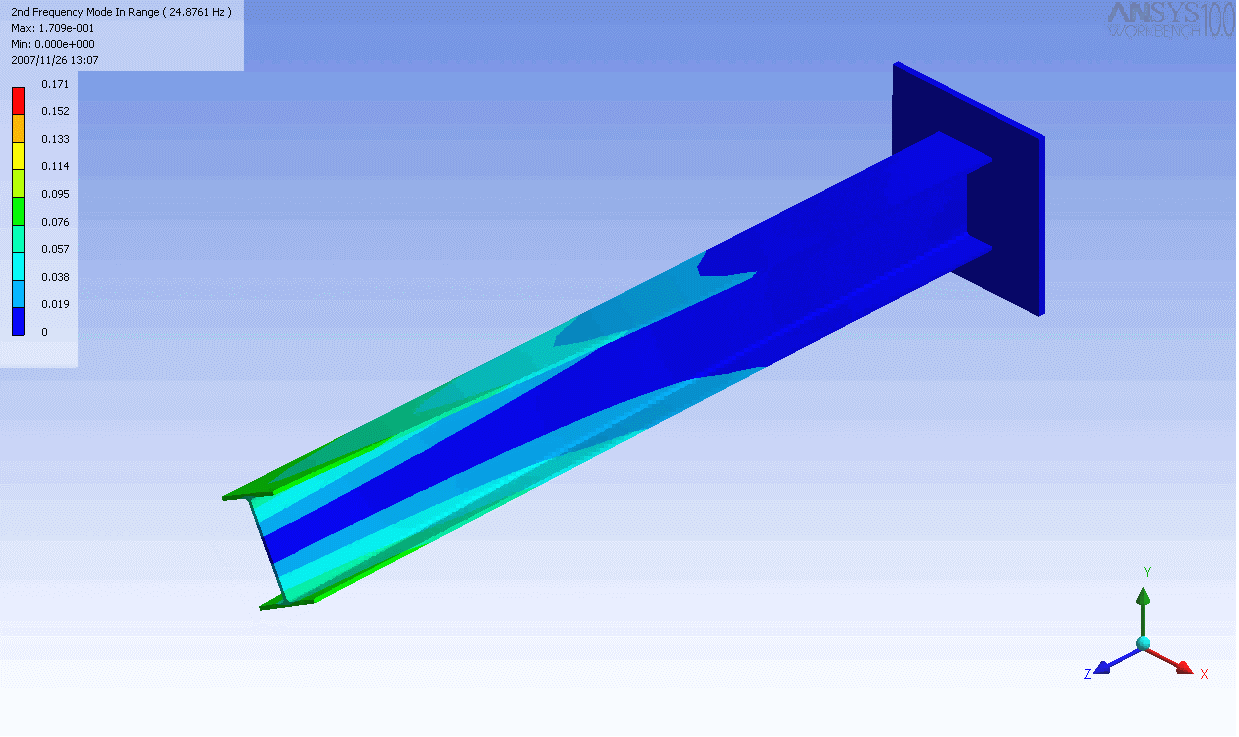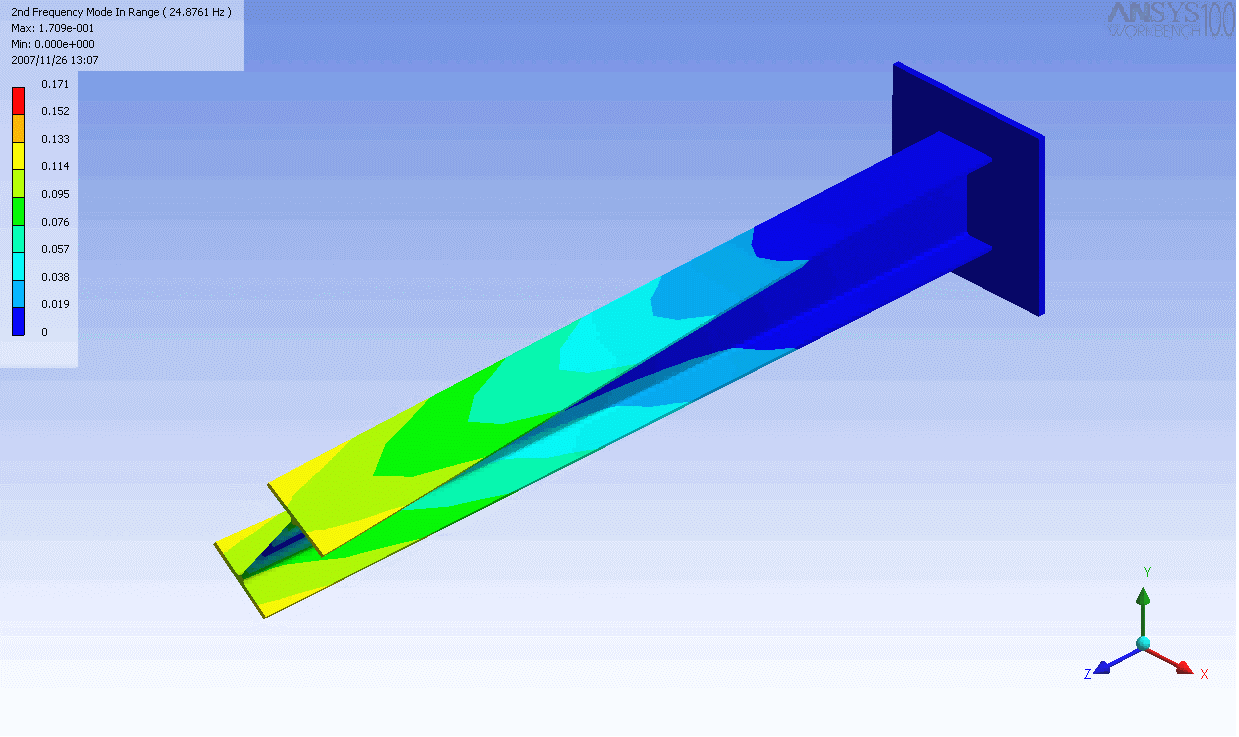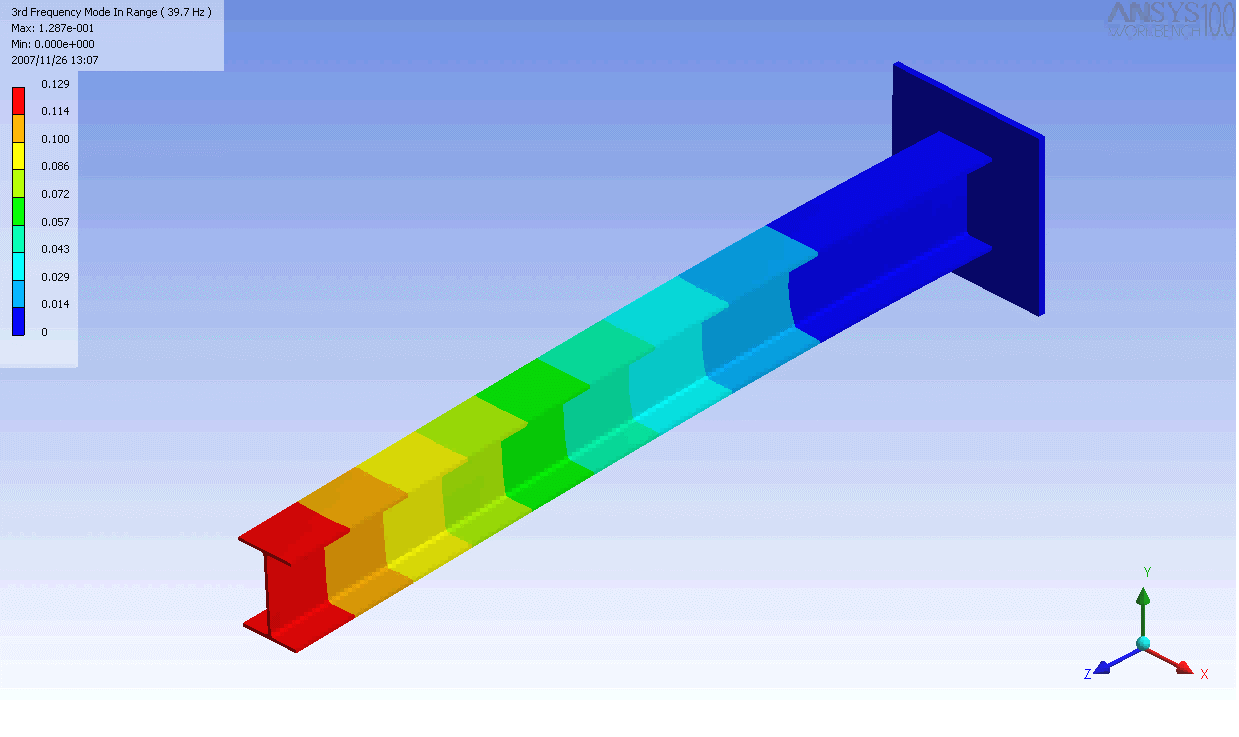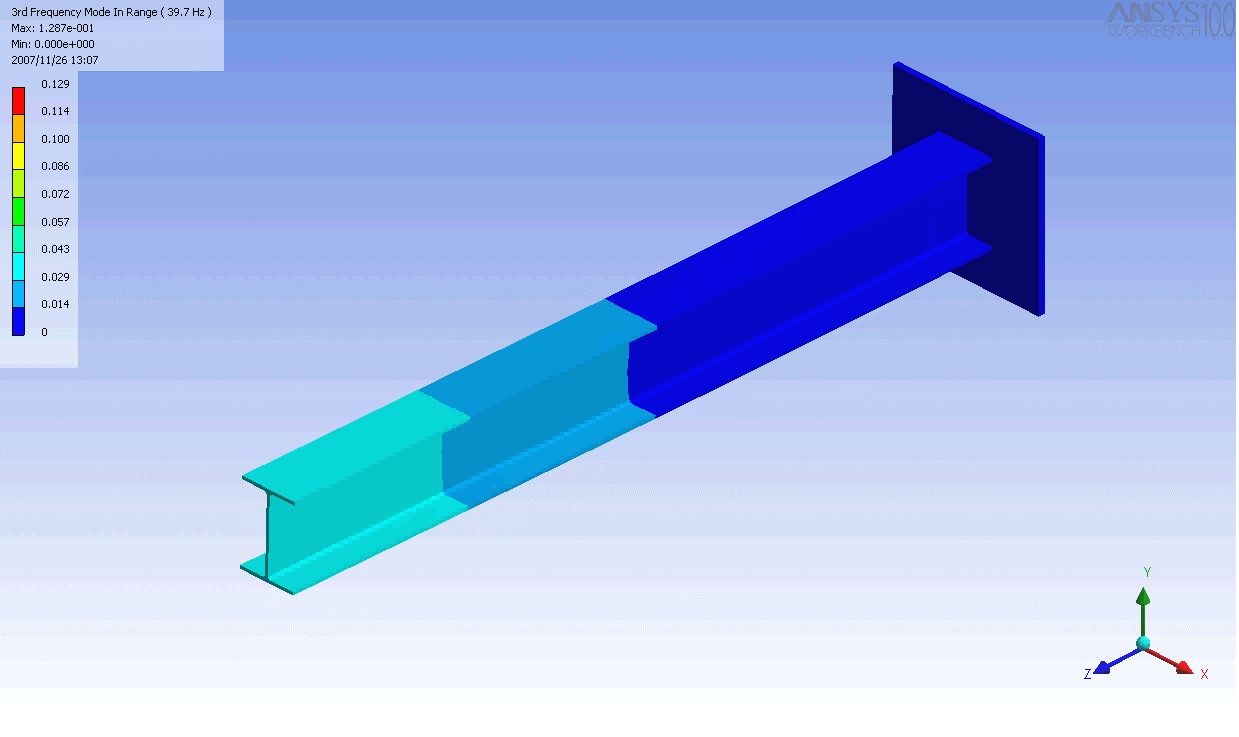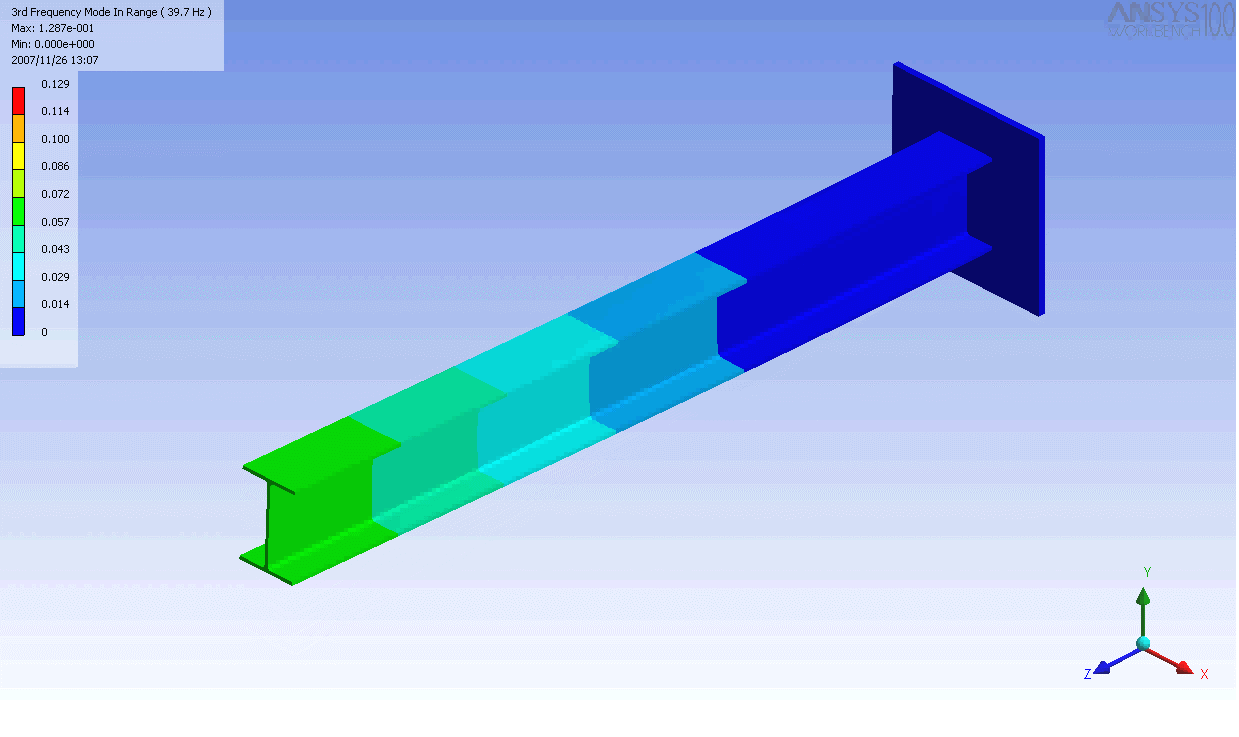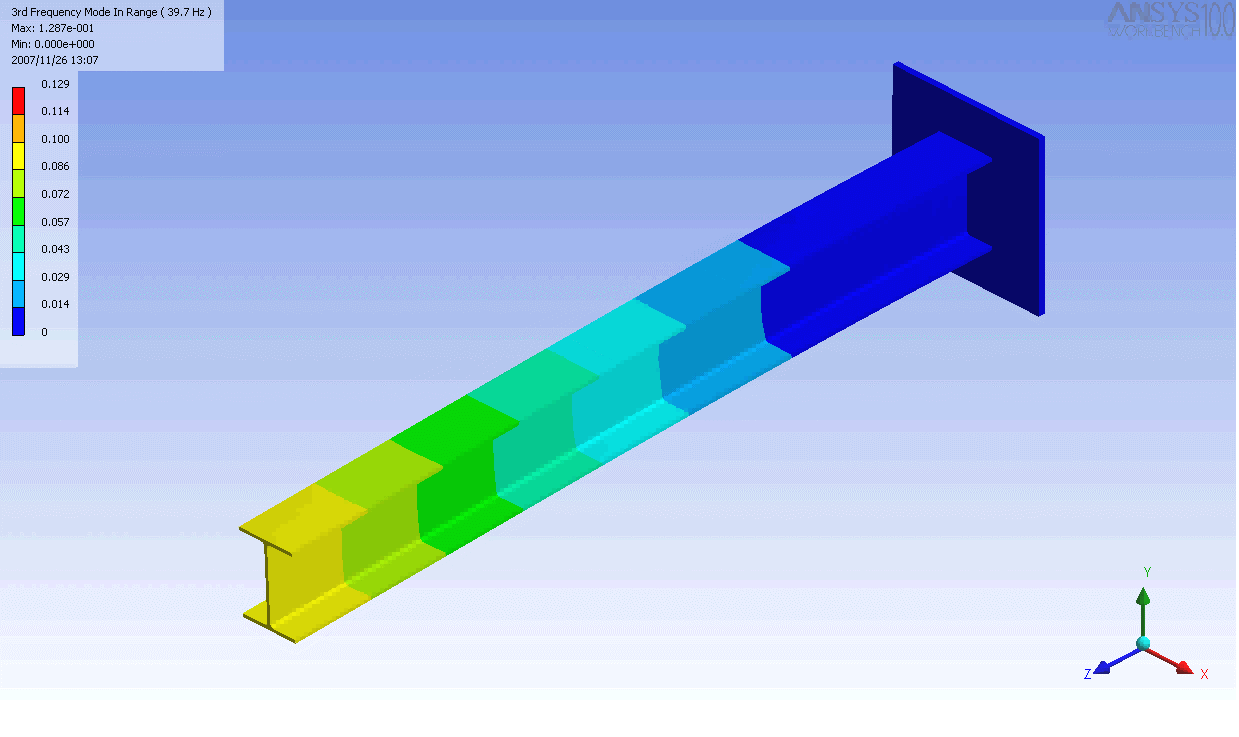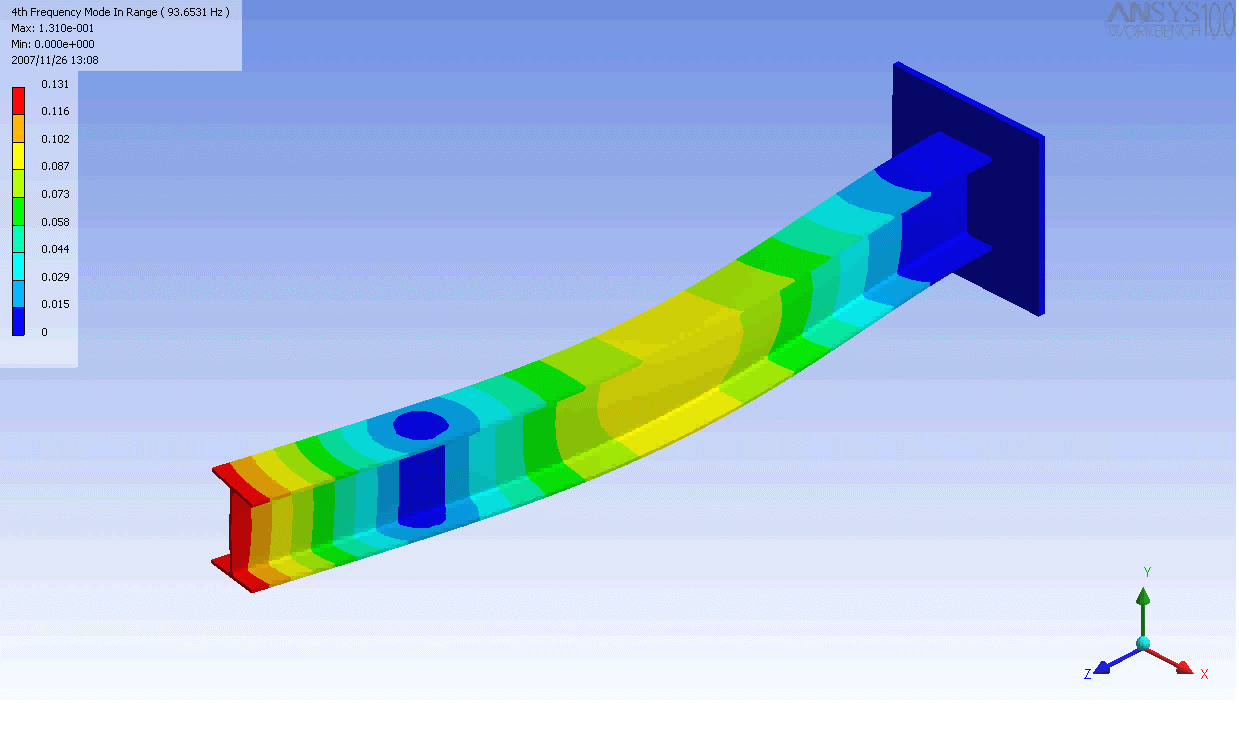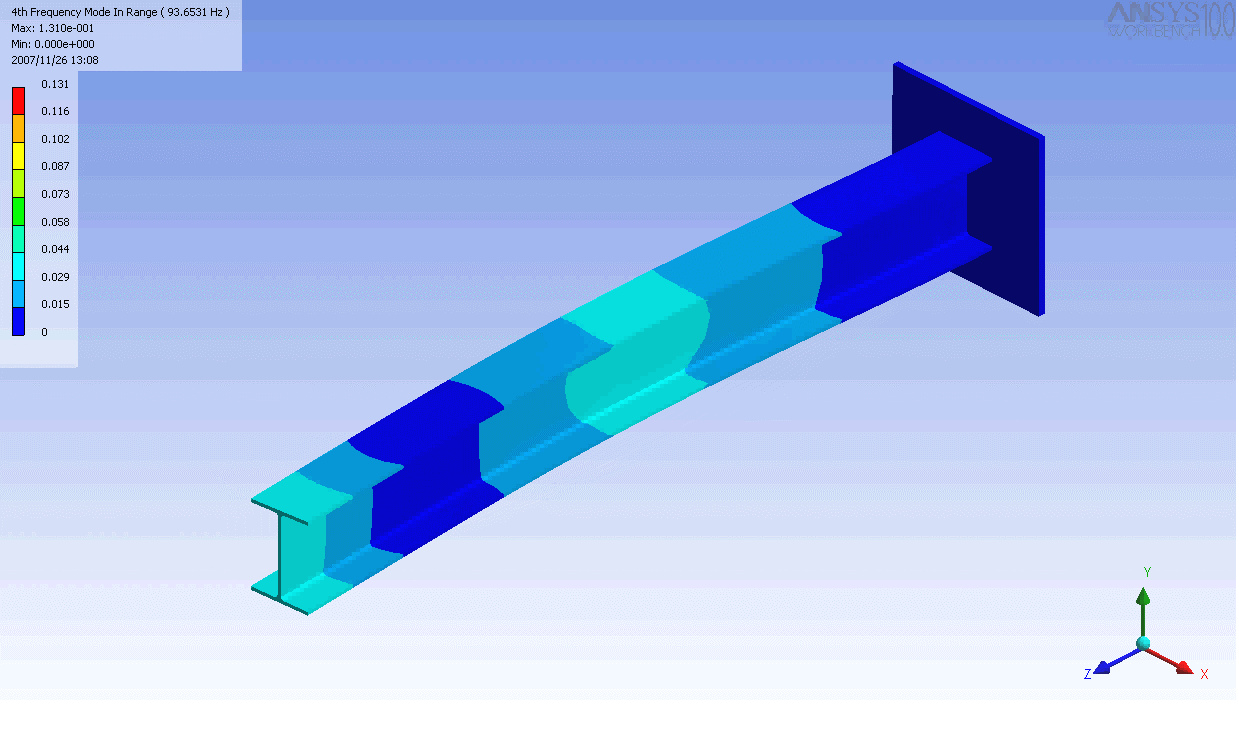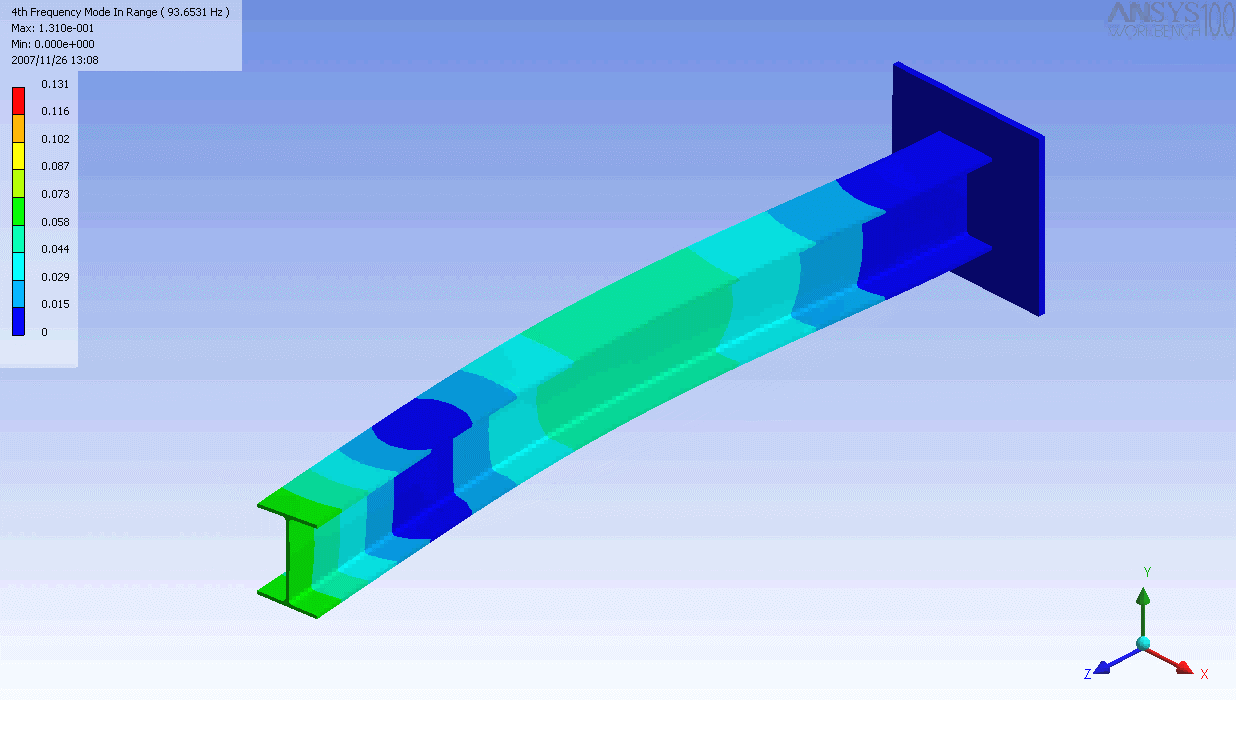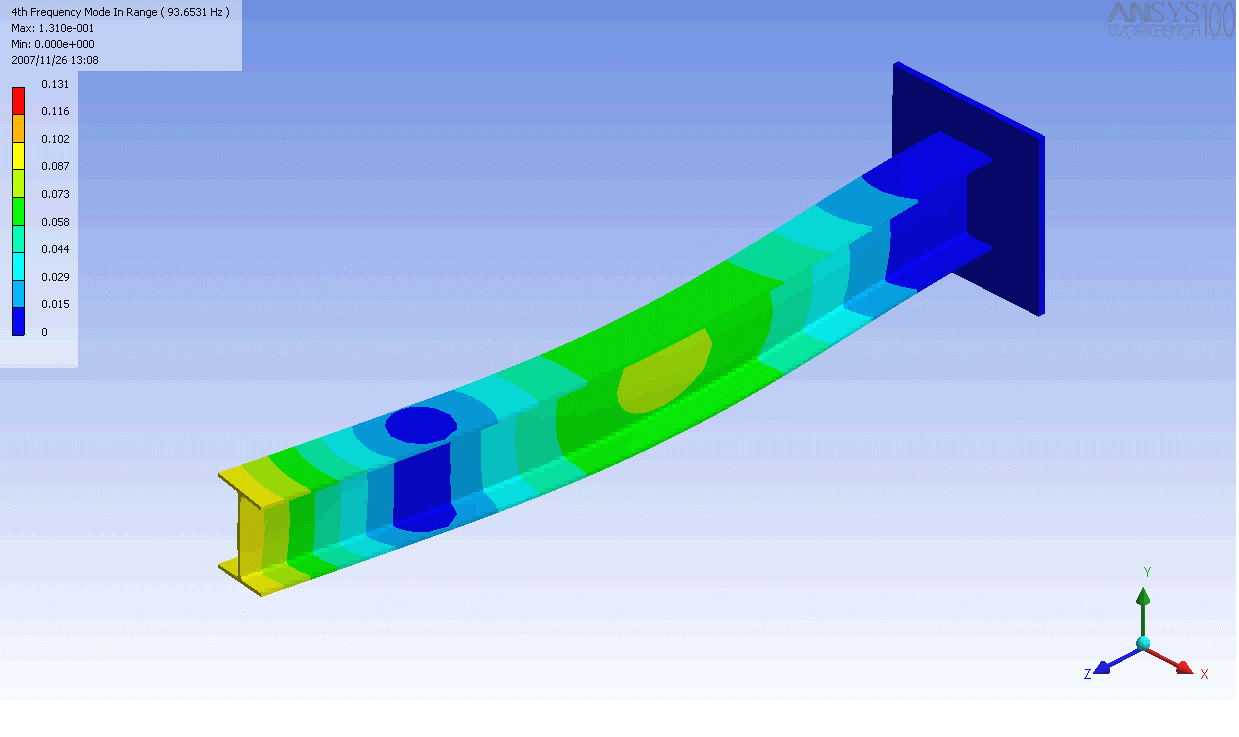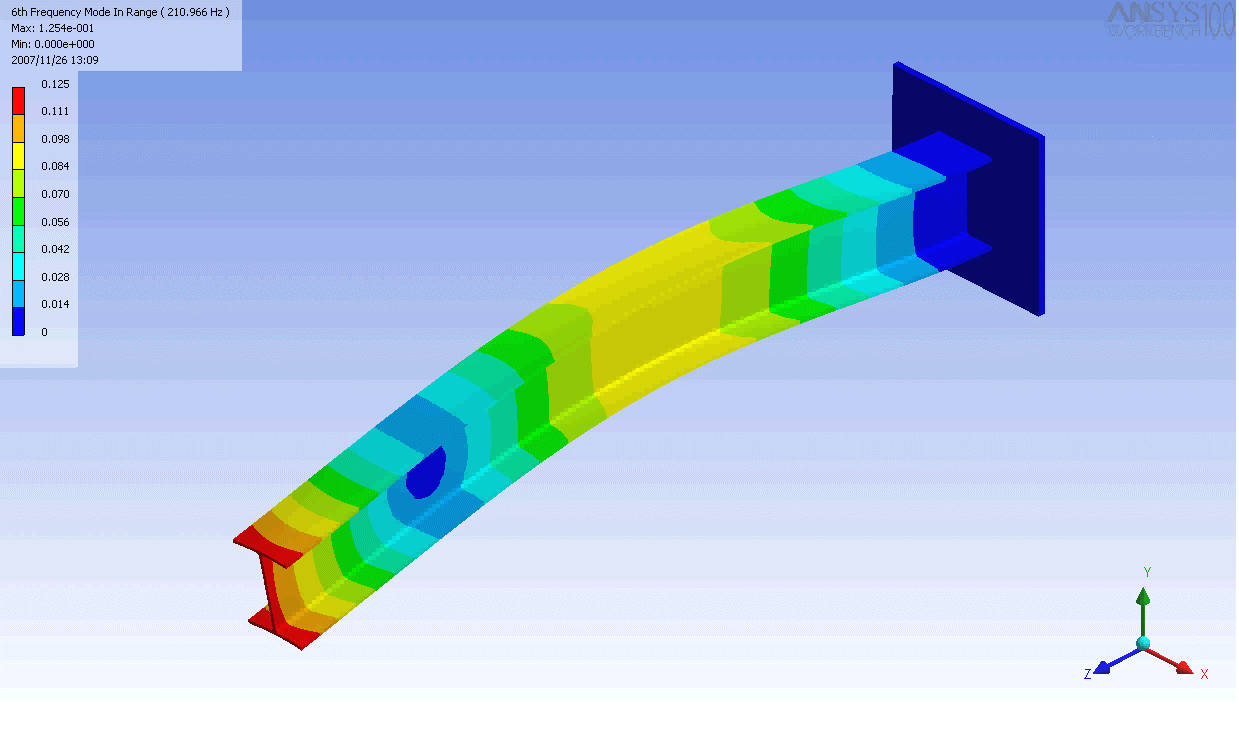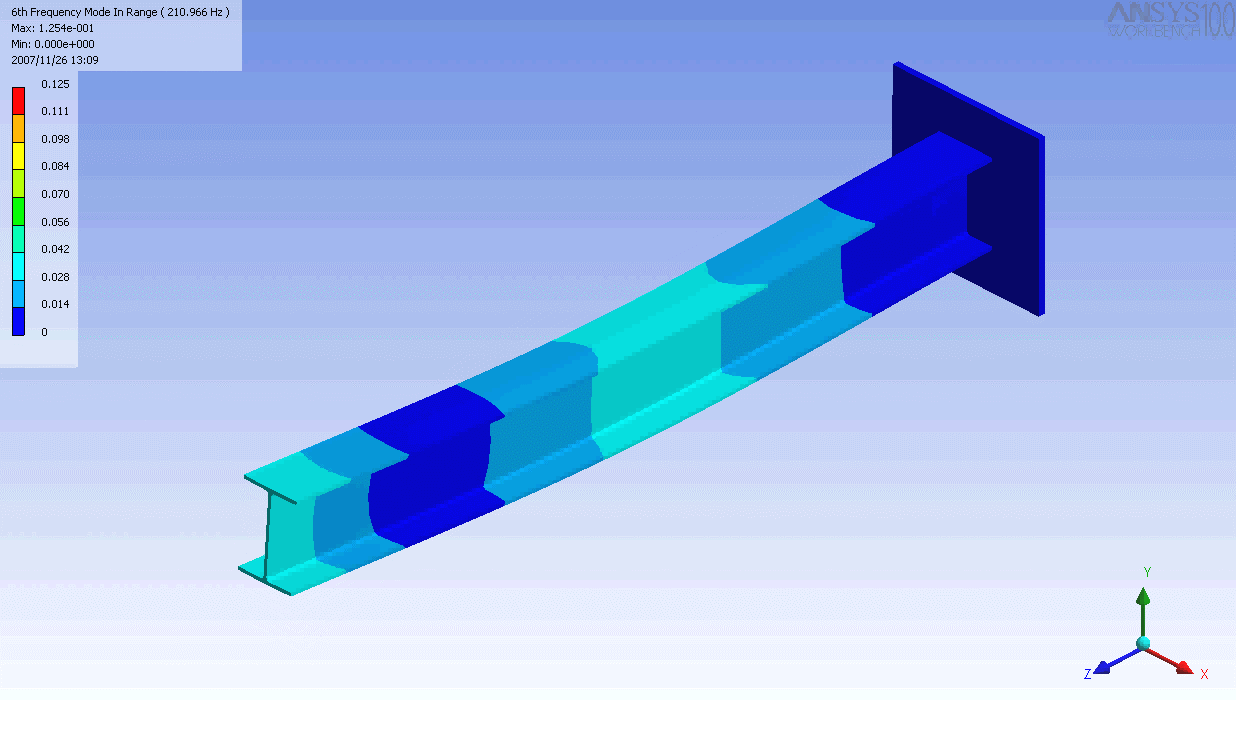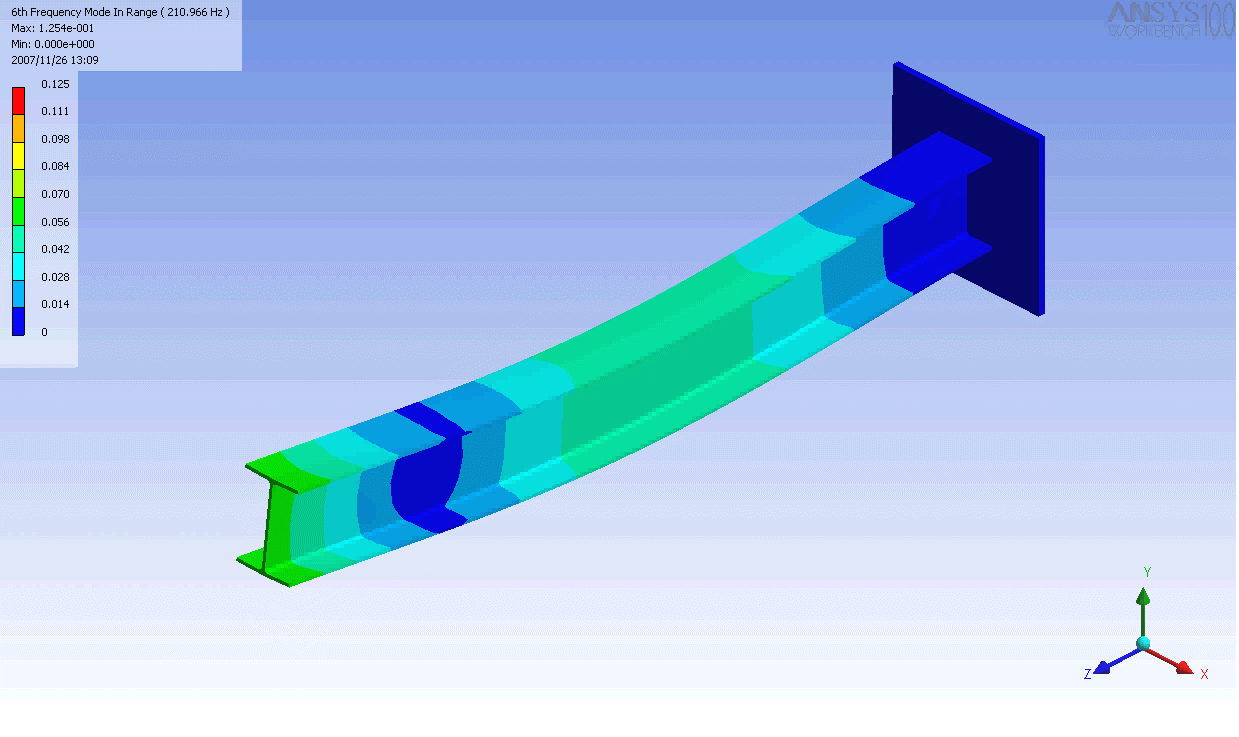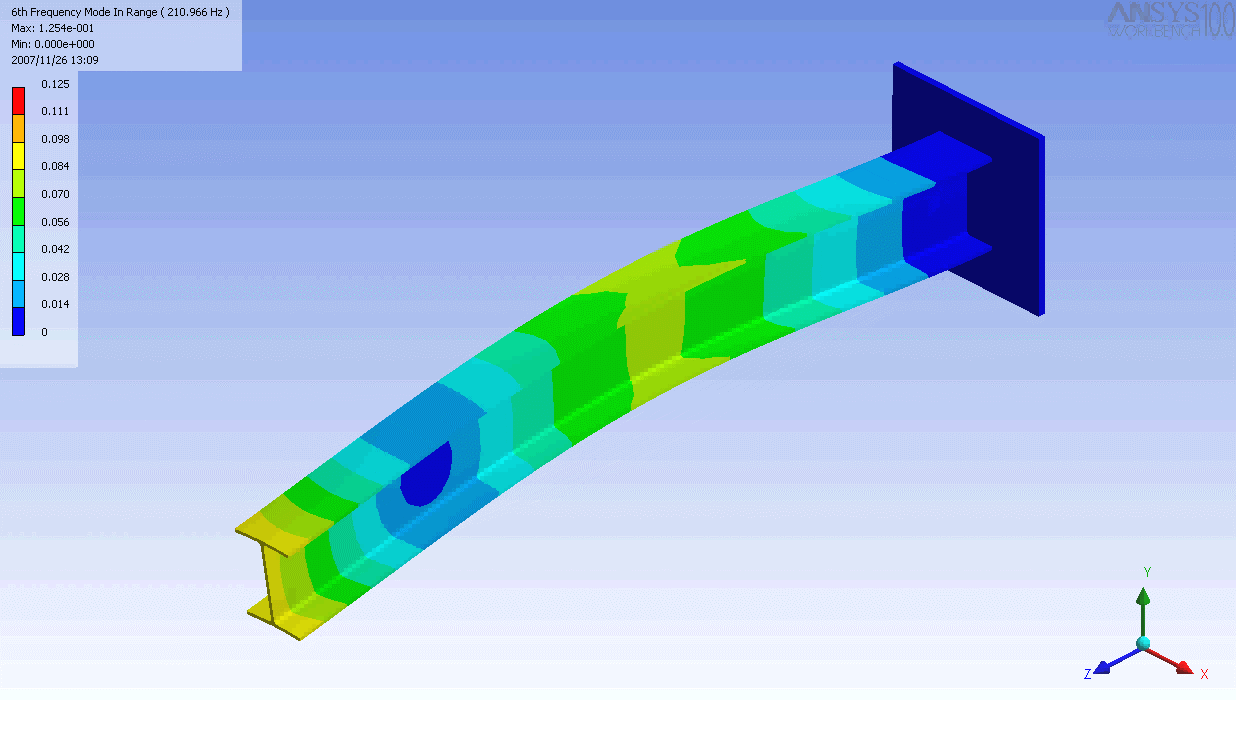5. 2. 티모셴코-레일리 이론

티모셴코는 1921년 보 방정식에 전단 효과를 추가하여 오일러-베르누이 보 이론을 개선했다. 티모셴코 이론의 운동학적 가정은 다음과 같다.

보의 축에 수직인 선은 변형 후에도 직선으로 유지된다.
변형 후 보의 두께는 변하지 않는다.

하지만, 축에 수직인 선이 변형 후에도 축에 수직으로 유지될 필요는 없다.

이러한 가정을 적용한 선형 탄성, 등방성, 균질한 균일 단면 보의 준정적 굽힘 방정식은 다음과 같다.^[12]

:

EI~\cfrac{\mathrm{d}^4 w}{\mathrm{d} x^4} = q(x) - \cfrac{EI}{k A G}~\cfrac{\mathrm{d}^2 q}{\mathrm{d} x^2}

여기서

I

는 단면의 단면 2차 모멘트,

A

는 단면적,

G

는 전단 탄성 계수,

k

는 '''전단 보정 계수''',

q(x)

는 가해지는 횡 하중이다. 푸아송 비(

\nu

)가 0.3에 가까운 재료의 경우, 직사각형 단면의 전단 보정 계수는 대략 다음과 같다.

:

k = \cfrac{5 + 5\nu}{6 + 5\nu}

수직선의 회전(

\varphi(x)

)은 다음 방정식으로 설명된다.

:

\cfrac{\mathrm{d}\varphi}{\mathrm{d}x} = -\cfrac{\mathrm{d}^2w}{\mathrm{d}x^2} -\cfrac{q(x)}{kAG}

굽힘 모멘트(

M

)와 전단력(

Q

)은 다음과 같이 주어진다.

:

M(x) = -EI~ \cfrac{\mathrm{d}\varphi}{\mathrm{d}x} ~;~~ Q(x) = kAG\left(\cfrac{\mathrm{d}w}{\mathrm{d}x}-\varphi\right) = -EI~\cfrac{\mathrm{d}^2\varphi}{\mathrm{d}x^2} = \cfrac{\mathrm{d}M}{\mathrm{d}x}

보의 동적 굽힘^[11]은 보의 굽힘 진동이라고도 하며, 18세기 말 다니엘 베르누이에 의해 처음 연구되었다. 베르누이의 진동 보에 대한 운동 방정식은 보의 고유 진동수를 과대 평가하는 경향이 있었고, 1877년 레일리에 의해 중간 평면 회전을 추가하여 약간 개선되었다. 1921년 스테판 티모셴코는 굽힘 보의 동적 응답에 대한 전단 효과를 통합하여 이론을 더욱 개선했다. 이를 통해 동적 오일러-베르누이 이론으로는 부적절한 높은 진동수의 문제를 해결하는 데 이론을 사용할 수 있었다.

1922년, 티모셴코는 전단 효과를 보 방정식에 추가하여 레일리가 제안한 동적 오일러-베르누이 보 이론을 개선했다. 티모셴코-레일리 이론에서는 보 중간 표면에 수직인 변형의 전단을 허용한다.^[12]^[13]

일정한 단면을 갖는 선형 탄성, 등방성, 균질 보의 굽힘 방정식은 다음과 같다.

:

\begin{align}& EI~\frac{\partial^4 w}{\partial x^4} + m~\frac{\partial^2 w}{\partial t^2} - \left(J + \frac{E I m}{k A G}\right)\frac{\partial^4 w}{\partial x^2~\partial t^2} + \frac{J m}{k A G}~\frac{\partial^4 w}{\partial t^4} \\[6pt]= {} & q(x,t) + \frac{J}{k A G}~\frac{\partial^2 q}{\partial t^2} - \frac{EI}{k A G}~\frac{\partial^2 q}{\partial x^2}\end{align}

여기서

J = \tfrac{mI}{A}

는 단면의 극 관성 모멘트이고,

m = \rho A

는 보의 단위 길이당 질량이며,

\rho

는 보의 밀도,

A

는 단면적,

G

는 전단 탄성 계수이고,

k

는 '''전단 보정 계수'''이다. 푸아송 비(

\nu

)가 0.3에 가까운 재료의 경우, 전단 보정 계수는 아래 표와 같다.

형상	전단 보정 계수 ( $k$ )
직사각형 단면	$\frac{5 + 5\nu}{6 + 5\nu}$
원형 단면	$\frac{6 + 12\nu + 6\nu^2}{7 + 12\nu + 4\nu^2}$

5. 2. 1. 자유 진동

1877년, 레일리는 보 단면의 회전 관성 효과를 포함하여 동적 오일러-베르누이 보 이론을 개선할 것을 제안했다. 1922년 티모셴코는 전단 효과를 보 방정식에 추가하여 그 이론을 더욱 개선했다. 티모셴코-레일리 이론에서는 보 중간 표면에 수직인 변형의 전단을 허용한다.^[12]^[13]

자유 조화 진동에 대한 티모셴코-레일리 방정식은 다음과 같다.

:

EI~\cfrac{\mathrm{d}^4 \hat{w}}{\mathrm{d} x^4} + m\omega^2\left(\cfrac{J}{m} + \cfrac{E I}{k A G}\right)\cfrac{\mathrm{d}^2 \hat{w}}{\mathrm{d} x^2} + m\omega^2\left(\cfrac{\omega^2 J}{k A G}-1\right)~\hat{w} = 0

이 방정식은

w

의 모든 도함수가 상쇄되기 위해 동일한 형태를 가져야 한다는 점을 고려하여 풀 수 있으며, 따라서

e^{kx}

형태의 해를 예상할 수 있다. 이러한 관찰은 특성 방정식으로 이어진다.

:

\alpha~k^4 + \beta~k^2 + \gamma = 0 ~;~~ \alpha := EI ~,~~ \beta := m\omega^2\left(\cfrac{J}{m} + \cfrac{E I}{k A G}\right) ~,~~ \gamma := m\omega^2\left(\cfrac{\omega^2 J}{k A G}-1\right)

이 사차 방정식의 해는 다음과 같다.

:

k_1 = +\sqrt{z_+} ~,~~ k_2 = -\sqrt{z_+} ~,~~ k_3 = +\sqrt{z_-} ~,~~ k_4 = -\sqrt{z_-}

여기서

:

z_+ := \cfrac{-\beta + \sqrt{\beta^2 - 4\alpha\gamma}}{2\alpha} ~,~~z_-:= \cfrac{-\beta - \sqrt{\beta^2 - 4\alpha\gamma}}{2\alpha}

자유 진동에 대한 티모셴코-레일리 보 방정식의 일반적인 해는 다음과 같이 쓸 수 있다.

:

\hat{w} = A_1~e^{k_1 x} + A_2~e^{-k_1 x} + A_3~e^{k_3 x} + A_4~e^{-k_3 x}

6. 판의 준정적 휨

변위, 중간 표면(빨간색) 및 중간 표면에 수직인 선(파란색)을 강조 표시하는 얇은 판의 변형

보는 한 차원이 다른 두 차원보다 훨씬 큰 특징을 가진다. 구조물이 평평하고 그 치수 중 하나가 다른 두 치수보다 훨씬 작을 때 이를 판이라고 한다. 적용된 하중 하에서 판의 변형과 응력을 설명하는 여러 이론이 있으며, 그 중 널리 사용되는 두 가지는 다음과 같다.

키르히호프-러브 판 이론(고전 판 이론)
민들린–레이스너 판 이론(판의 1차 전단 이론)^[1]

6. 1. 키르히호프-러브 판 이론

보는 한 차원이 다른 두 차원보다 훨씬 큰 특징을 가집니다. 구조물이 평평하고 그 치수 중 하나가 다른 두 치수보다 훨씬 작을 때 이를 판이라고 합니다. 적용된 하중 하에서 판의 변형과 응력을 설명하는 여러 이론이 있으며, 그중 널리 사용되는 두 가지는 다음과 같습니다.

키르히호프-러브 판 이론 (고전 판 이론이라고도 함)
민들린–레이스너 판 이론 (판의 1차 전단 이론이라고도 함)

키르히호프-러브 평판 이론의 가정은 다음과 같습니다.

중간면에 수직인 직선은 변형 후에도 직선으로 유지됩니다.
중간면에 수직인 직선은 변형 후에도 중간면에 수직으로 유지됩니다.
평판의 두께는 변형 동안 변하지 않습니다.

이러한 가정은 다음을 의미합니다.

:

\begin{align}u_\alpha(\mathbf{x}) & = - x_3~\frac{\partial w^0}{\partial x_\alpha}= - x_3~w^0_{,\alpha} ~;~~\alpha=1,2 \\u_3(\mathbf{x}) & = w^0(x_1, x_2)\end{align}

여기서

\mathbf{u}

는 평판 내 점의 변위이고,

w^0

는 중간면의 변위입니다.

변형률-변위 관계는 다음과 같습니다.

:

\begin{align}\varepsilon_{\alpha\beta} & =

x_3~w^0_{,\alpha\beta} \\

\varepsilon_{\alpha 3} & = 0 \\\varepsilon_{33} & = 0\end{align}

평형 방정식은 다음과 같습니다.

:

M_{\alpha\beta,\alpha\beta} + q(x) = 0 ~;~~ M_{\alpha\beta} := \int_{-h}^h x_3~\sigma_{\alpha\beta}~dx_3

여기서

q(x)

는 평판 표면에 수직으로 작용하는 하중입니다.

변위로 표현하면, 외부 하중이 없는 등방성 선형 탄성 평판에 대한 평형 방정식은 다음과 같이 쓸 수 있습니다.

:

w^0_{,1111} + 2~w^0_{,1212} + w^0_{,2222} = 0

직접 텐서 표기법으로,

:

\nabla^2\nabla^2 w = 0

6. 2. 민들린-레이스너 판 이론

민들린-레이스너 판 이론은 판의 1차 전단 이론이라고도 불리며, 전단 변형을 고려한 판 이론이다. 이 이론에서는 중간 표면에 수직인 선이 변형 후에도 직선을 유지하고 늘어나지 않지만, 반드시 중간 표면에 수직일 필요는 없다는 가정을 사용한다.

판의 변위는 다음과 같이 나타낼 수 있다.

:

u_\alpha(\mathbf{x})  = - x_3~\varphi_\alpha ~;~~\alpha=1,2 \\u_3(\mathbf{x})  = w^0(x_1, x_2)

여기서

\varphi_\alpha

는 법선의 회전을 나타낸다.

이러한 가정을 통해 얻은 변형률-변위 관계는 다음과 같다.

:

\varepsilon_{\alpha\beta}  =

x_3~\varphi_{\alpha,\beta} \\

\varepsilon_{\alpha 3} = \cfrac{1}{2}~\kappa\left(w^0_{,\alpha}- \varphi_\alpha\right) \\\varepsilon_{33} = 0

여기서

\kappa

는 전단 보정 계수이다.

평형 방정식은 다음과 같다.

:

M_{\alpha\beta,\beta}-Q_\alpha = 0 \\Q_{\alpha,\alpha}+q = 0

여기서

:

Q_\alpha := \kappa~\int_{-h}^h \sigma_{\alpha 3}~dx_3

7. 판의 동적 휨

보의 특징은 한 차원이 다른 두 차원보다 훨씬 "크다"는 것이다. 구조물이 평평하고 그 치수 중 하나가 다른 두 치수보다 훨씬 "작을" 때 이를 판이라고 한다. 적용된 하중 하에서 판의 변형과 응력을 설명하려는 여러 이론이 있으며, 그 중 널리 사용되는 두 가지는 다음과 같다.

키르히호프-러브 판 이론(고전 판 이론)
민들린–레이스너 판 이론(판의 1차 전단 이론)

판의 동역학 이론은 판에서 파동의 전파, 정상파 및 진동 모드 연구를 결정한다.

7. 1. 얇은 키르히호프 판의 동역학

판의 동역학 이론은 판에서 파동의 전파, 정상파 및 진동 모드 연구를 결정한다. 키르히호프 판의 동적 굽힘을 지배하는 방정식은 다음과 같다.

:

M_{\alpha\beta,\alpha\beta} - q(x,t) = J_1~\ddot{w}^0 - J_3~\ddot{w}^0_{,\alpha\alpha}

여기서, 밀도

\rho = \rho(x)

인 판의 경우,

:

J_1 := \int_{-h}^h \rho~dx_3  ~;~~J_3 := \int_{-h}^h x_3^2~\rho~dx_3

그리고

:

\ddot{w}^0 = \frac{\partial^2 w^0}{\partial t^2} ~;~~\ddot{w}^0_{,\alpha\beta} = \frac{\partial^2 \ddot{w}^0}{\partial x_\alpha\, \partial x_\beta}

아래 그림은 원형 판의 일부 진동 모드를 보여준다.

참조

_[1] 서적 Advanced mechanics of materials John Wiley and Sons 1993
_[2] 서적 Theory of plates and shells McGraw-Hill 1959
_[3] 서적 The nonlinear theory of elastic shells Cambridge University Press 1998
_[4] 서적 Mechanical Engineering Design McGraw Hill 1986
_[5] 서적 Mechanics of Materials PWS Publishing Company 1997
_[6] 서적 Advanced Mechanics of Materials Macmillan Publishing Company 1995
_[7] 서적 Beams on Elastic Foundation Ann Arbor, University of Michigan Studies 1946
_[8] 서적 Design Analysis of Beams, Circular Plates and Cylindrical Tanks on Elastic Foundations Taylor & Francis Group 2006
_[9] 서적 Analysis of Beams and Frames on Elastic Foundation Trafford Publishing
_[10] 서적 Handbook of Structures on Elastic Foundation VSB - Technical University of Ostrava 2013
_[11] 논문 Dynamics of transversely vibrating beams using four engineering theories 1999
_[12] 서적 Theory of Vibration with Applications 1981
_[13] 논문 On Timoshenko's correction for shear in vibrating isotropic beams 1977

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com