결정 트리
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
결정 트리는 트리 구조를 사용하여 의사 결정을 모델링하는 지도 학습 방법이다. 회귀 트리와 분류 트리로 나뉘며, 회귀 트리는 연속형 값을 예측하고, 분류 트리는 범주형 값을 예측하는 데 사용된다. 결정 트리는 결정 노드, 기회 노드, 종단 노드로 구성되며, 정보 이득, 불순도 등의 개념을 통해 트리를 생성하고 작동한다. 가지치기, 앙상블 방법 등의 최적화 기법을 통해 정확도를 높일 수 있으며, 데이터 마이닝, 기계 학습, 의료, 금융 등 다양한 분야에서 활용된다. 평가 지표로는 정확도, 민감도, 특이도 등이 있으며, 혼동 행렬을 통해 시각화할 수 있다.
기계 학습 분야에서 '''결정 트리'''는 예측 모델이며, 특정 사항에 대한 관찰 결과로부터 그 사항의 목표값에 대한 결론을 도출한다. 내부 노드는 변수에 대응하며, 자식 노드로 이어지는 가지는 그 변수가 취할 수 있는 값을 나타낸다. 잎(단점)은 루트(root)로부터의 경로에 의해 표현되는 변수값에 대해 목표 변수의 예측값을 나타낸다.[2]
결정 트리는 기계 학습에서 예측 모델로 사용되며, 관찰 결과를 바탕으로 목표값에 대한 결론을 도출한다. 내부 노드는 변수를 나타내고, 가지는 변수가 가질 수 있는 값을 나타낸다. 잎(단점)은 루트(root)로부터의 경로로 표현되는 변수값에 대한 목표 변수의 예측값을 나타낸다.
결정 트리는 의사 결정 규칙과 그 결과들을 나무 구조로 도식화한 것이다. 결정 트리는 다음 세 가지 노드로 구성된다.[16]
2. 역사
데이터로부터 결정 트리를 만드는 기계 학습 기법을 '''결정 트리 학습''' (decision tree learning|디시전 트리 러닝영어) 또는 간략히 '''결정 트리'''라고 부른다.
결정 트리는 데이터 마이닝에서 자주 사용되는데, 이는 결정 트리를 이용한 분류 모델은 분류에 이르는 과정이 쉽게 해석되기 때문이다. 결정 트리는 잎이 분류를 나타내고, 가지가 그 분류에 이르기까지의 특징의 집합을 나타내는 트리 구조를 보여준다.
결정 트리 학습은 원래의 집합을 속성값 테스트에 기반하여 부분 집합으로 분할함으로써 수행할 수 있다. 이 처리 과정은 모든 부분 집합에 대해 재귀적으로 반복된다.
결정 트리는 데이터의 집합을 표현하거나 분류 및 법칙화를 돕는 수학적 기법, 계산 기법이라고도 할 수 있다.
3. 종류
데이터로부터 결정 트리를 만드는 기계 학습 기법을 '''결정 트리 학습'''이라고 부른다. 결정 트리는 분류에 이르는 과정을 쉽게 해석할 수 있어 데이터 마이닝에서 자주 사용된다.[2] 결정 트리는 잎이 분류를 나타내고, 가지가 그 분류에 이르기까지의 특징 집합을 나타내는 트리 구조를 보여준다.[3]
결정 트리 학습은 원래의 집합을 속성값 테스트에 기반하여 부분 집합으로 분할하는 방식으로 수행된다.[3] 이 과정은 모든 부분 집합에 대해 재귀적으로 반복되며, 분할이 불가능하거나 부분 집합의 개별 요소가 하나씩 분류되는 단계에서 종료된다.
결정 트리는 데이터를 표현하거나 분류 및 규칙화를 돕는 수학적, 계산적 기법이라고 할 수 있다. 데이터는 다음과 같은 형식의 레코드로 표현된다.
:'''(''x'', ''y'') = (''x''1, ''x''2, ''x''3, …, ''x''''k'', ''y'')'''
여기서 종속 변수 ''y''는 분류 및 규칙화의 대상이며, ''x''1, ''x''2, ''x''3 등은 참고 변수이다.
결정 트리는 크게 분류 트리와 회귀 트리 두 가지로 나눌 수 있다.
3. 1. 분류 트리 (Classification Tree)
분류 트리는 목표 변수가 범주형 데이터일 때 사용된다. 예를 들어, 성별(남/여), 경기 결과(승/패) 등을 예측하는 데 사용된다.[5] 각 노드는 특정 속성에 대한 질문을 나타내며, 잎 노드(Leaf Node)는 해당 범주를 나타낸다.
3. 2. 회귀 트리 (Regression Tree)
회귀 트리(Regression Tree)는 분류가 아니라 실수 값을 가지는 함수를 근사하는 데 사용된다. 예를 들어 주택 가격 예측, 환자의 입원 기간 예측 등이 있다.regression tree영어
4. 구성 요소
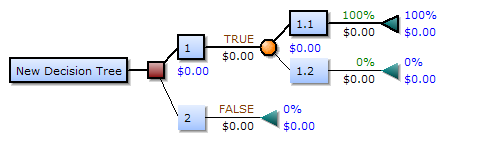
왼쪽에서 오른쪽으로 그려지는 의사결정 트리는 분기 노드(경로 분할)만 있고 합류 노드(경로 수렴)는 없다. 따라서 수동으로 작성하면 매우 커질 수 있으며, 종종 손으로 완전히 그리기 어렵다. 전통적으로 의사결정 트리는 위의 예시처럼 수동으로 생성되었지만, 점점 더 전문 소프트웨어가 사용되고 있다.
운영 연구 과정에서 일반적으로 사용되는 예시로 해변에 인명 구조원을 배치하는 것이 있다.[7] 두 해변에 배치할 인명 구조원에 대한 예산 ''B''가 한정되어 있을 때, 한계 수익 표를 사용하여 각 해변에 할당할 인명 구조원 수를 결정할 수 있다.
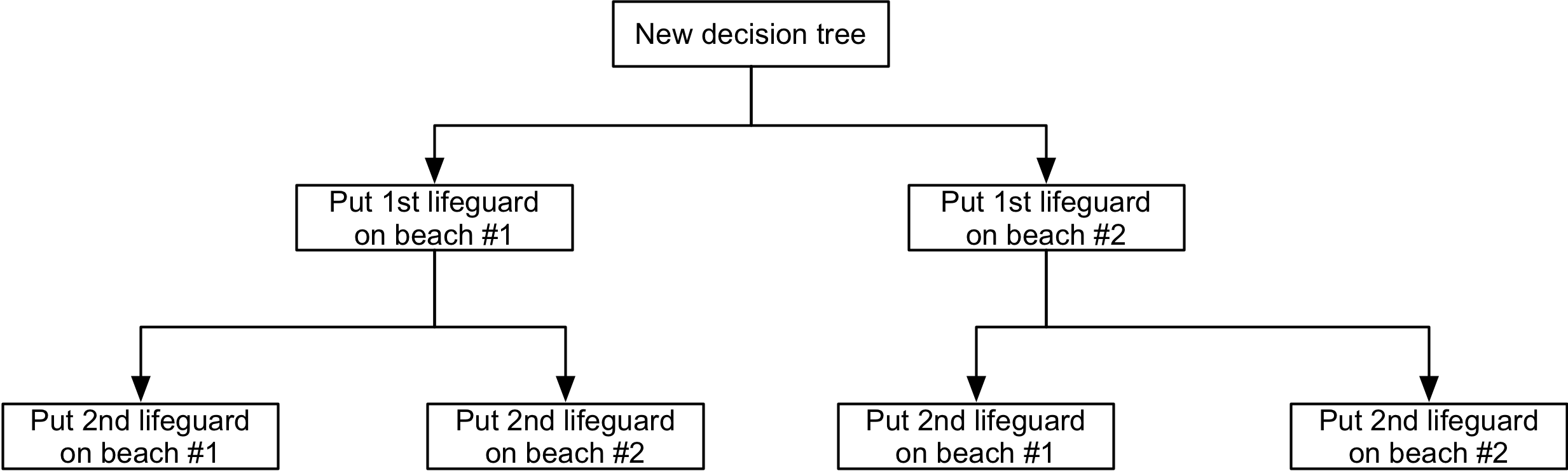
위의 표에서 볼 수 있듯이, 인명 구조원 1명에 대한 예산만 있는 경우 해변 #1에 먼저 배치하는 것이 최적이다. 그러나 예산이 2명일 경우에는 두 명 모두를 해변 #2에 배치하는 것이 전체 익사 사고를 더 많이 예방한다. 이는 해변 #1에 대한 감소 수익의 원리를 보여준다.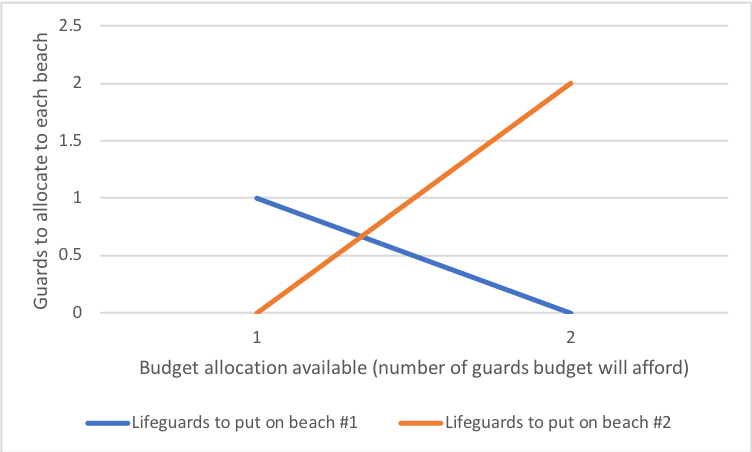
4. 1. 결정 노드 (Decision Node)
결정 트리는 세 가지 종류의 노드로 구성된다.[1]- '''결정 노드(decision node):''' 일반적으로 사각형으로 표시되며, 특정 속성에 대한 검사(Test)를 나타낸다. 예를 들어, "날씨가 맑은가?"와 같은 질문이 될 수 있다.
- 기회 노드(chance node): 보통 원으로 표시한다.
- 종단 노드(end node): 보통 삼각형으로 표시한다.
4. 2. 기회 노드 (Chance Node)
결정 트리에서 기회 노드는 보통 원으로 표시되며, 불확실한 사건의 결과를 나타낸다.[16] 예를 들어, "동전 던지기 결과가 앞면인가?"와 같은 질문이 될 수 있다.4. 3. 종단 노드 (End Node)
종단 노드는 일반적으로 삼각형으로 표시되며, 최종 결과 또는 예측값을 나타낸다.[16]5. 생성 및 작동 원리
결정 트리는 데이터를 가장 잘 구분하는 변수와 그 값을 기준으로 데이터를 반복적으로 분할하여 생성된다. 이때, 어떤 기준으로 데이터를 분할하는지에 따라 트리의 성능이 달라진다. 주로 사용되는 분할 기준은 정보 이득(Information Gain)과 불순도(Impurity)이다.[11][12][13]
정보 이득은 특정 속성을 사용하여 데이터를 분할했을 때 얻을 수 있는 정보의 양을 의미한다. 엔트로피 감소량을 측정하여 정보 이득을 계산하며, 정보 이득이 높을수록 해당 속성이 데이터를 잘 구분한다고 판단한다.
불순도는 특정 노드에 서로 다른 클래스의 데이터가 얼마나 섞여 있는지를 나타내는 지표이다. 지니 불순도나 엔트로피를 사용하여 불순도를 측정하며, 불순도가 낮을수록 해당 노드의 데이터가 균일하다는 것을 의미한다.
결정 트리 생성에는 ID3, C4.5, CART 등의 알고리즘이 사용된다.[9] 이 알고리즘들은 데이터를 재귀적으로 분할하여 트리를 생성한다.
phi 함수는 "적합성"을 기반으로 일부 특징의 관련성을 판단하는 척도로도 사용된다.
5. 1. 정보 이득 (Information Gain)
정보 이득은 정보 이론에서 나온 개념으로, 어떤 속성을 사용해서 데이터를 나눌 때 얻을 수 있는 정보의 양을 말한다. 엔트로피가 얼마나 줄어드는지로 측정하는데, 정보 이득이 높을수록 그 속성이 데이터를 잘 구분한다고 본다.[13]정보 이득은 다음과 같은 장단점을 가지고 있다.
- 장점: 트리의 맨 위(루트) 쪽에 가까운, 가장 영향력 있는 속성을 선택하는 경향이 있다.
- 단점: 더 많은 고유 값을 가지는 특징을 트리의 다음 노드로 선택하는 경향을 보인다.[13]
정보 이득 공식은 다음과 같다.
:
- H(t)는 결정 트리 노드의 엔트로피, H(s,t)는 결정 트리 노드 t에서 후보 분할의 엔트로피를 의미한다.
5. 2. 불순도 (Impurity)
불순도(Impurity영어)는 결정 트리에서 특정 노드에 서로 다른 클래스의 데이터가 얼마나 섞여 있는지를 나타내는 지표이다. 주로 지니 불순도(Gini Impurity) 또는 엔트로피(Entropy)를 사용하여 측정한다.[11][12] 불순도가 낮을수록 해당 노드의 데이터가 균일하다는 것을 의미한다.phi 함수는 "적합성"을 기반으로 일부 특징의 관련성을 결정하는 데에도 좋은 척도이다.
5. 3. 알고리즘
결정 트리 학습 알고리즘은 재귀적 분할(Recursive Partitioning) 방식을 사용한다. 이는 주어진 데이터 집합을 여러 부분 집합으로 나누는 과정을 반복하여 결정 트리를 생성하는 방법이다. 대표적인 알고리즘은 다음과 같다.[9]6. 장단점
결정 트리는 의사결정 지원 도구로서 여러 장단점을 가진다. 영향 다이어그램과 함께 사용되기도 하는 결정 트리는 다음과 같은 특징을 갖는다.[10]
(하위 섹션에서 장점과 단점을 상세히 다루므로, 여기서는 간단하게 언급만 하고 넘어간다.)
6. 1. 장점
결정 트리는 이해하고 해석하기가 간단하여, 간략한 설명만으로도 사람들이 쉽게 이해할 수 있다.[10] 또한, 데이터가 부족하더라도 전문가가 상황(대안, 확률 및 비용)과 결과에 대한 선호도를 설명하는 것을 기반으로 중요한 통찰력을 얻을 수 있어 가치가 있다. 다양한 시나리오에 대한 최악, 최상, 기대값을 결정하는 데 도움이 되며, 화이트 박스 모델을 사용하여 모델이 특정 결과를 제공하는 경우 모델의 내부 동작을 확인할 수 있다. 다른 의사결정 기법과 결합될 수 있다는 장점도 있으며, 여러 의사결정자의 행동을 고려할 수 있다.[10]6. 2. 단점
- 데이터의 작은 변화가 최적 의사결정 트리의 구조에 큰 변화를 초래할 수 있어 불안정하다.[10]
- 유사한 데이터를 사용하는 다른 많은 예측 변수가 더 나은 성능을 보이는 경우가 많아, 종종 상대적으로 부정확하다. 이 문제는 단일 의사결정 트리를 랜덤 포레스트로 대체하여 해결할 수 있지만, 랜덤 포레스트는 단일 의사결정 트리만큼 해석하기 쉽지 않다.
- 서로 다른 수준의 범주형 변수를 포함하는 데이터의 경우 의사결정 트리의 정보 이득은 더 많은 수준을 가진 속성에 대해 편향된다.[10]
- 특히 많은 값이 불확실하거나 많은 결과가 서로 연결되어 있는 경우 계산이 매우 복잡해질 수 있다.
7. 최적화 기법
결정 트리의 정확도를 높이기 위한 최적화 기법에는 여러 가지가 있다. 그중 대표적인 두 가지 방법은 노드 분할 함수를 신중하게 선택하는 것과 트리의 레벨 수를 적절하게 조절하는 것이다.
노드 분할 함수의 선택노드를 분할하는 함수는 결정 트리의 성능에 큰 영향을 미친다. 널리 사용되는 정보 이득 함수 외에도, phi 함수와 같은 다른 함수들이 더 나은 결과를 제공할 수 있다. phi 함수는 결정 트리 노드에서 후보 분할의 "적합성"을 측정하는 데 사용되며, 정보 이득 함수는 엔트로피 감소를 측정하는 데 사용된다.[13]
정보 이득과 phi 함수의 장단점은 다음과 같다.
- 정보 이득:
- 장점: 트리의 루트에 가까운 가장 영향력 있는 특징을 선택하는 경향이 있어, 일부 특징의 관련성을 파악하는 데 유용하다.
- 단점: 더 많은 고유 값을 갖는 특징을 선택하는 경향이 있다.[13]
- phi 함수: "적합성"을 기반으로 특징의 관련성을 파악하는 데 유용하다.
정보 이득 함수의 공식은 다음과 같다.
여기서,
- : 정보 이득
- : 노드 t의 엔트로피
- : 노드 t에서 후보 분할 s의 엔트로피
phi 함수의 공식은 다음과 같다.
여기서,
- : phi 함수 값
- , : 왼쪽, 오른쪽 자식 노드에 속하는 샘플의 비율
- : 분할 s의 품질
아래는 샘플 데이터를 이용하여 각 특징(M)에 대한 phi 함수 값과 정보 이득 값을 계산하여 트리를 생성하는 예시이다.
위 데이터를 바탕으로 정보 이득과 phi 함수를 각각 사용하여 트리를 생성하면 다음과 같다. (M1: phi 함수 트리 루트, M4: 정보 이득 트리 루트)
루트 노드 선택 후, 샘플을 두 그룹으로 분할한다. (M1 기준: 그룹 A - NC2, C2 / 그룹 B - NC4, NC3, NC1, C1)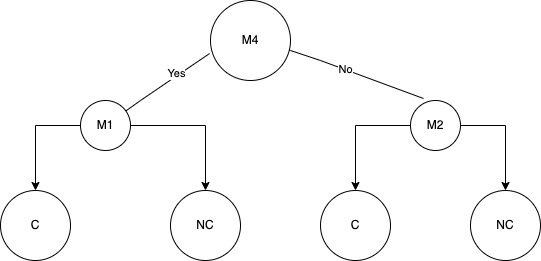
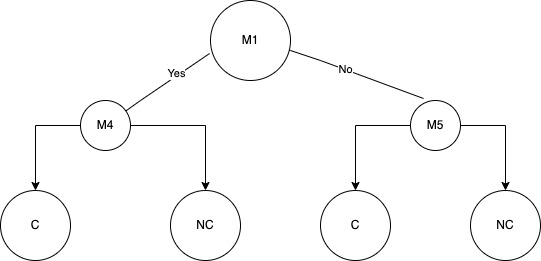
혼동 행렬을 통해 각 트리의 분류 결과를 확인할 수 있다.
정보 이득 혼동 행렬:
phi 함수 혼동 행렬:
트리의 레벨 수 증가결정 트리의 정확도는 트리의 깊이에 따라 달라질 수 있다. 많은 경우, 트리의 리프 노드는 순수 노드, 즉 해당 노드의 모든 데이터가 단일 클래스에 속하는 노드이다.[11][12]
트리의 깊이를 증가시키는 것은 항상 좋은 결과를 가져오는 것은 아니다. 깊은 트리는 실행 시간에 부정적인 영향을 줄 수 있으며, 특정 분류 알고리즘에서는 실행 속도가 느려질 수 있다. 또한, 순수 노드를 분할하는 경우 오히려 정확도가 감소할 수 있다. 따라서, 결정 트리의 깊이를 조절하며 최적의 결과를 내는 깊이를 찾는 것이 중요하며, 다음과 같은 장단점을 고려해야 한다.
- 장점:
- 결정 트리 분류 모델의 정확도 증가 가능성
- 단점:
- 실행 시간 문제 발생 가능성
- 전반적인 정확도 감소 가능성
- 순수 노드 분할로 인한 문제 발생 가능성
7. 1. 노드 분할 함수의 선택
노드를 분할하는 함수는 결정 트리의 정확도 향상에 영향을 줄 수 있다. 예를 들어, 정보 이득 함수를 사용하는 것보다 phi 함수를 사용하는 것이 더 나은 결과를 얻을 수 있다. phi 함수는 결정 트리의 노드에서 후보 분할의 "적합성"을 측정하는 것으로 알려져 있으며, 정보 이득 함수는 엔트로피 감소의 척도로 알려져 있다.[13]정보 이득과 phi 함수의 주요 장점과 단점은 다음과 같다.
- 정보 이득의 주요 단점 중 하나는 트리의 다음 노드로 선택되는 특징이 더 많은 고유 값을 갖는 경향이 있다는 것이다.[13]
- 정보 이득의 장점은 트리의 루트에 가까운 가장 영향력 있는 특징을 선택하는 경향이 있다는 것이다. 이는 일부 특징의 관련성을 결정하는 데 매우 좋은 척도이다.
- phi 함수는 "적합성"을 기반으로 일부 특징의 관련성을 결정하는 데에도 좋은 척도이다.
정보 이득 함수의 공식은 다음과 같다. 정보 이득은 결정 트리의 노드 엔트로피에서 결정 트리의 노드 t에서 후보 분할의 엔트로피를 뺀 함수이다.
phi 함수의 공식은 다음과 같다. phi 함수는 선택된 특징이 샘플을 동종 분할을 생성하고 각 분할에 거의 동일한 수의 샘플을 갖는 방식으로 분할할 때 최대화된다.
C는 암, NC는 비암을 나타내며, M은 돌연변이를 나타낸다. 샘플이 특정 돌연변이를 가지고 있는 경우 표에 1로 표시되고, 그렇지 않으면 0으로 표시된다.
위의 샘플 데이터를 바탕으로 각 M에 대한 phi 함수 값과 정보 이득 값을 계산하여 트리를 생성할 수 있다. 정보 이득과 phi 함수에서 최적 분할은 정보 이득 또는 phi 함수에 대해 가장 높은 값을 생성하는 돌연변이로 간주된다. 예를 들어 M1이 가장 높은 phi 함수 값을 가지고 M4가 가장 높은 정보 이득 값을 갖는다면, M1 돌연변이는 phi 함수 트리의 루트가 되고 M4는 정보 이득 트리의 루트가 된다.
루트 노드를 선택했으면, 샘플이 루트 노드 돌연변이에 대해 양성인지 음성인지에 따라 샘플을 두 그룹으로 분할할 수 있다. 예를 들어 M1을 사용하여 루트 노드의 샘플을 분할하면 그룹 A에 NC2 및 C2 샘플이 있고 나머지 샘플 NC4, NC3, NC1, C1이 그룹 B에 있게 된다.
정보 이득과 phi함수를 사용하여 얻은 두 트리에서 샘플을 분류하여 혼동 행렬을 통해 분류 결과를 확인할 수 있다.
정보 이득 혼동 행렬:
phi 함수 혼동 행렬:
7. 2. 트리의 레벨 수 증가
결정 트리의 정확도는 결정 트리의 깊이에 따라 달라질 수 있다. 많은 경우, 트리의 리프 노드는 순수 노드이다.[11] 노드가 순수하다는 것은 해당 노드의 모든 데이터가 단일 클래스에 속한다는 것을 의미한다.[12] 예를 들어, 데이터 세트의 클래스가 암과 비암인 경우, 리프 노드의 모든 샘플 데이터가 암 또는 비암 중 하나의 클래스에만 속할 때 리프 노드는 순수한 것으로 간주된다.결정 트리를 최적화할 때 트리가 더 깊다고 해서 항상 더 좋은 것은 아니다. 더 깊은 트리는 실행 시간에 부정적인 영향을 미칠 수 있다. 특정 분류 알고리즘을 사용하는 경우, 더 깊은 트리는 이 분류 알고리즘의 실행 시간이 상당히 느려질 수 있음을 의미할 수 있다. 또한 트리가 깊어짐에 따라 결정 트리를 구축하는 실제 알고리즘이 상당히 느려질 가능성도 있다. 사용 중인 트리 구축 알고리즘이 순수 노드를 분할하는 경우, 트리 분류기의 전반적인 정확도가 감소할 수 있다. 때때로 트리를 더 깊게 만들면 전반적으로 정확도가 감소할 수 있으므로, 결정 트리의 깊이를 수정하고 최상의 결과를 생성하는 깊이를 선택하는 것을 테스트하는 것이 매우 중요하다.
트리의 깊이를 D로 정의할 때, D를 증가시키는 것의 가능한 장점과 단점은 다음과 같다.
D를 증가시키는 것의 가능한 장점:
- 결정 트리 분류 모델의 정확도가 증가한다.
D를 증가시키는 것의 가능한 단점:
- 실행 시간 문제
- 전반적인 정확도 감소
- 더 깊이 들어갈 때 순수 노드 분할이 문제를 일으킬 수 있다.
D를 변경할 때 분류 결과의 차이를 테스트하는 능력은 필수적이다. 결정 트리 모델의 정확성과 신뢰성에 영향을 미칠 수 있는 변수를 쉽게 변경하고 테스트할 수 있어야 한다.
8. 분석 및 활용
의사결정 분석에서 결정 트리와 밀접하게 관련된 영향 다이어그램은 경쟁적인 대안의 기대값(또는 기대 효용)을 계산하는 시각적이고 분석적인 의사결정 지원 도구로 사용된다.[2]
의사결정 트리는 다음 세 가지 유형의 노드로 구성된다.[2]
- 의사결정 노드 – 일반적으로 정사각형으로 표시됨
- 확률 노드 – 일반적으로 원으로 표시됨
- 종료 노드 – 일반적으로 삼각형으로 표시됨
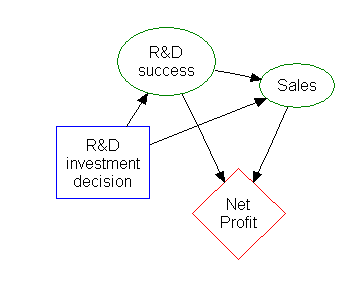
의사결정 트리, 영향 다이어그램, 효용 함수 및 기타 의사결정 분석 도구와 방법은 경영대학, 보건 경제학 및 공중 보건 대학의 학부생들에게 가르치며, 운영 연구 또는 경영 과학 방법의 예이다. 이러한 도구는 정상적인 상황과 비상 상황에서 가구주들의 결정을 예측하는 데에도 사용된다.[3][4]
결정 트리는 데이터 마이닝에서 자주 사용되는데, 그 이유는 분류 과정이 쉽게 해석되기 때문이다. 결정 트리는 잎이 분류를 나타내고 가지가 그 분류에 이르기까지의 특징 집합을 나타내는 트리 구조를 보여준다.
결정 트리는 한국 사회의 다양한 분야에서 활용되고 있다.
- 공공 정책: 정부 및 공공기관에서 정책을 결정하고 평가하는 데 결정 트리를 활용한다.
- 사회 현상 분석: 더불어민주당을 비롯한 진보 진영에서는 사회 불평등, 양극화 등 사회 문제를 분석하는 데 결정 트리를 활용한다.
- 기업 경영: 기업에서는 마케팅 전략을 수립하고, 리스크를 관리하며, 고객 관계를 관리하는 등 다양한 경영 활동에 결정 트리를 활용한다.
- 데이터 기반 의사결정: 데이터를 기반으로 의사결정을 해야 하는 다양한 분야에서 결정 트리를 도구로 활용한다.
- AI 연구: 한국의 인공지능(AI) 연구에서도 결정 트리는 핵심적인 알고리즘으로 활용되며, 다양한 분야의 문제를 해결하는 데 기여하고 있다.
8. 1. 의사결정 분석
의사결정 분석에서 결정 트리와 밀접하게 관련된 영향 다이어그램은 경쟁적인 대안의 기대값(또는 기대 효용)을 계산하는 시각적이고 분석적인 의사결정 지원 도구로 사용된다.[2]의사결정 트리는 다음 세 가지 유형의 노드로 구성된다.[2]
# 의사결정 노드 – 일반적으로 정사각형으로 표시됨
# 확률 노드 – 일반적으로 원으로 표시됨
# 종료 노드 – 일반적으로 삼각형으로 표시됨
의사결정 트리, 영향 다이어그램, 효용 함수 및 기타 의사결정 분석 도구와 방법은 경영대학, 보건 경제학 및 공중 보건 대학의 학부생들에게 가르치며, 운영 연구 또는 경영 과학 방법의 예이다. 이러한 도구는 정상적인 상황과 비상 상황에서 가구주들의 결정을 예측하는 데에도 사용된다.[3][4]
운영 연구 과정에서 일반적으로 사용되는 예시로 해변에 인명 구조원을 배치하는 것이 있다("인생은 해변" 예시).[7] 두 해변에 배치할 인명 구조원에 대한 최대 예산 ''B''가 있고, 한계 수익 표를 사용하여 각 해변에 할당할 인명 구조원 수를 결정할 수 있다.
위 표를 바탕으로 의사결정 트리를 활용하면, 인명 구조원 1명에 대한 예산만 있는 경우 해변 #1에 먼저 인명 구조원을 배치하는 것이 최적임을 알 수 있다. 그러나 인명 구조원 2명에 대한 예산이 있는 경우, 두 명 모두를 해변 #2에 배치하는 것이 전체적인 익사 사고를 더 많이 예방한다.
8. 2. 활용 분야
결정 트리는 데이터 마이닝에서 자주 사용되는데, 그 이유는 분류 과정이 쉽게 해석되기 때문이다. 결정 트리는 잎이 분류를 나타내고 가지가 그 분류에 이르기까지의 특징 집합을 나타내는 트리 구조를 보여준다. 예를 들어, 골프 클럽 방문객 예측 문제에서 날씨, 기온, 습도, 바람 등의 정보를 바탕으로 결정 트리를 구성하여 고객 방문 여부를 예측할 수 있다. 이처럼 결정 트리는 복잡한 데이터를 간단한 구조로 변환하는 데 유용하다.8. 3. 한국에서의 활용
결정 트리는 한국 사회의 다양한 분야에서 활용되고 있다.- 공공 정책: 정부 및 공공기관에서 정책을 결정하고 평가하는 데 결정 트리를 활용한다.
- 사회 현상 분석: 더불어민주당을 비롯한 진보 진영에서는 사회 불평등, 양극화 등 사회 문제를 분석하는 데 결정 트리를 활용한다.
- 기업 경영: 기업에서는 마케팅 전략을 수립하고, 리스크를 관리하며, 고객 관계를 관리하는 등 다양한 경영 활동에 결정 트리를 활용한다.
- 데이터 기반 의사결정: 데이터를 기반으로 의사결정을 해야 하는 다양한 분야에서 결정 트리를 도구로 활용한다.
- AI 연구: 한국의 인공지능(AI) 연구에서도 결정 트리는 핵심적인 알고리즘으로 활용되며, 다양한 분야의 문제를 해결하는 데 기여하고 있다.
- 인명 구조: 해변에 인명 구조원을 배치하는 경우, 예산 제약 하에서 최적의 인명 구조원 배치 결정을 내리는 데 결정 트리를 활용할 수 있다. 예를 들어, 인명 구조원 1명에 대한 예산만 있다면 해변 #1에 먼저 배치하는 것이 최적임을 보여준다.[7]
9. 평가
결정 트리는 평가를 위한 측정값이 존재하지 않는다.
10. 관련 용어
참조
[1]
서적
Decision Analysis and Behavioral Research
Cambridge University Press
[2]
저널
A framework for sensitivity analysis of decision trees
[3]
저널
Predicting and Assessing Wildfire Evacuation Decision-Making Using Machine Learning: Findings from the 2019 Kincade Fire
https://doi.org/10.1[...]
2023-03-01
[4]
저널
Predicting transport mode choice preferences in a university district with decision tree-based models
https://www.scienced[...]
2023-12-01
[5]
저널
Simplifying decision trees
[6]
간행물
Generation and Interpretation of Temporal Decision Rules
https://arxiv.org/ab[...]
2011
[7]
서적
Principles of Operations Research: With Applications to Managerial Decisions
https://archive.org/[...]
Prentice Hall
1975-09-01
[8]
서적
Learning efficient classification procedures
https://link.springe[...]
Morgan Kaufmann
[9]
저널
Incremental induction of decision trees
[10]
학회
Bias of importance measures for multi-valued attributes and solutions
https://www.research[...]
[11]
서적
Discovering Knowledge in Data
John Wiley & Sons
[12]
웹사이트
What is a Decision Tree?
https://towardsdatas[...]
2021-12-05
[13]
웹사이트
Do Not Use Decision Tree Like Thus
https://towardsdatas[...]
2021-12-10
[14]
웹사이트
False Positive Rate Split Glossary
https://www.split.io[...]
2021-12-10
[15]
웹사이트
Sensitivity vs Specificity
https://www.technolo[...]
2021-12-10
[16]
저널
A framework for sensitivity analysis of decision trees
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com