늘린 오각뿔

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 공식
3. 성질
4. 쌍대 다면체
5. 관련 다면체
참조

1. 개요

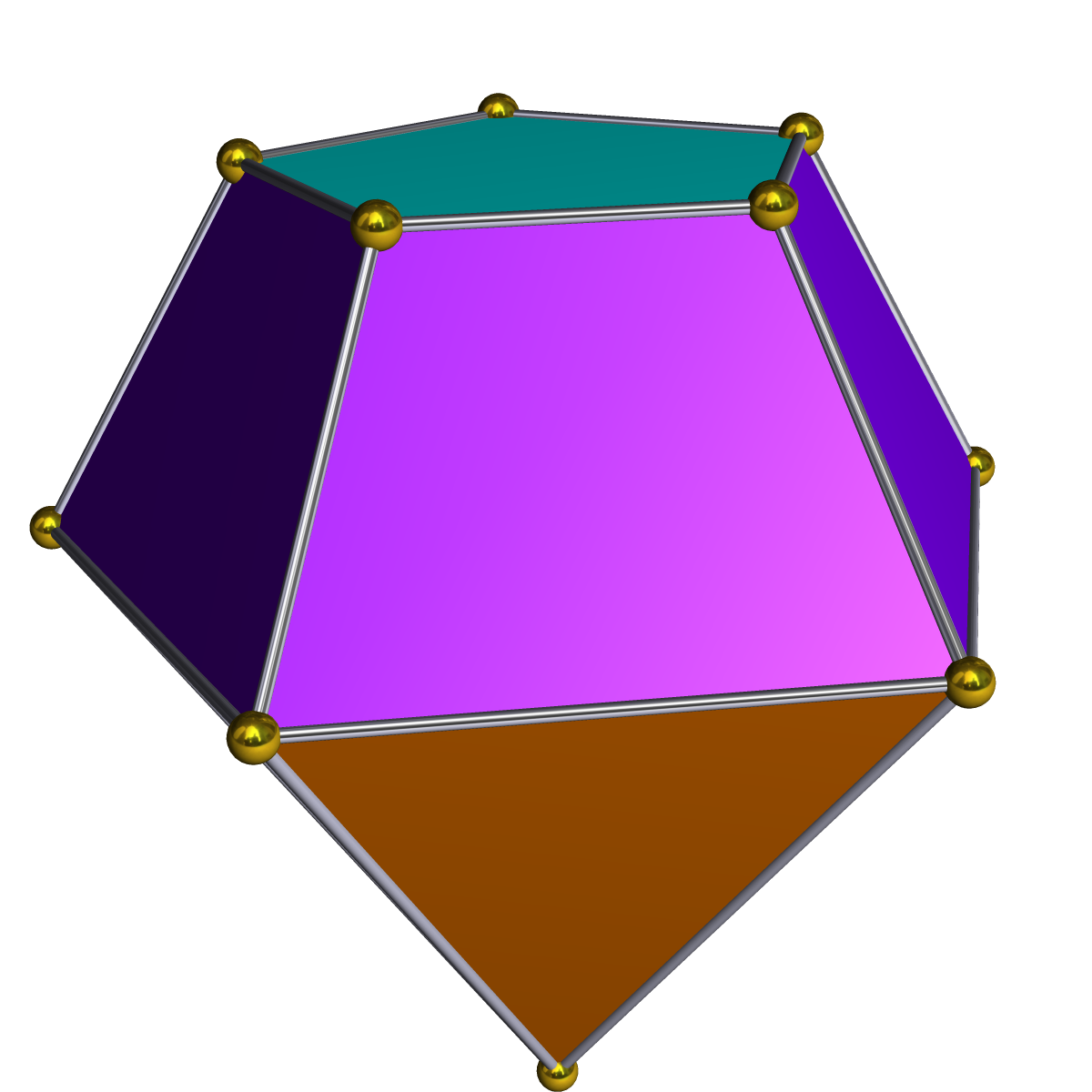
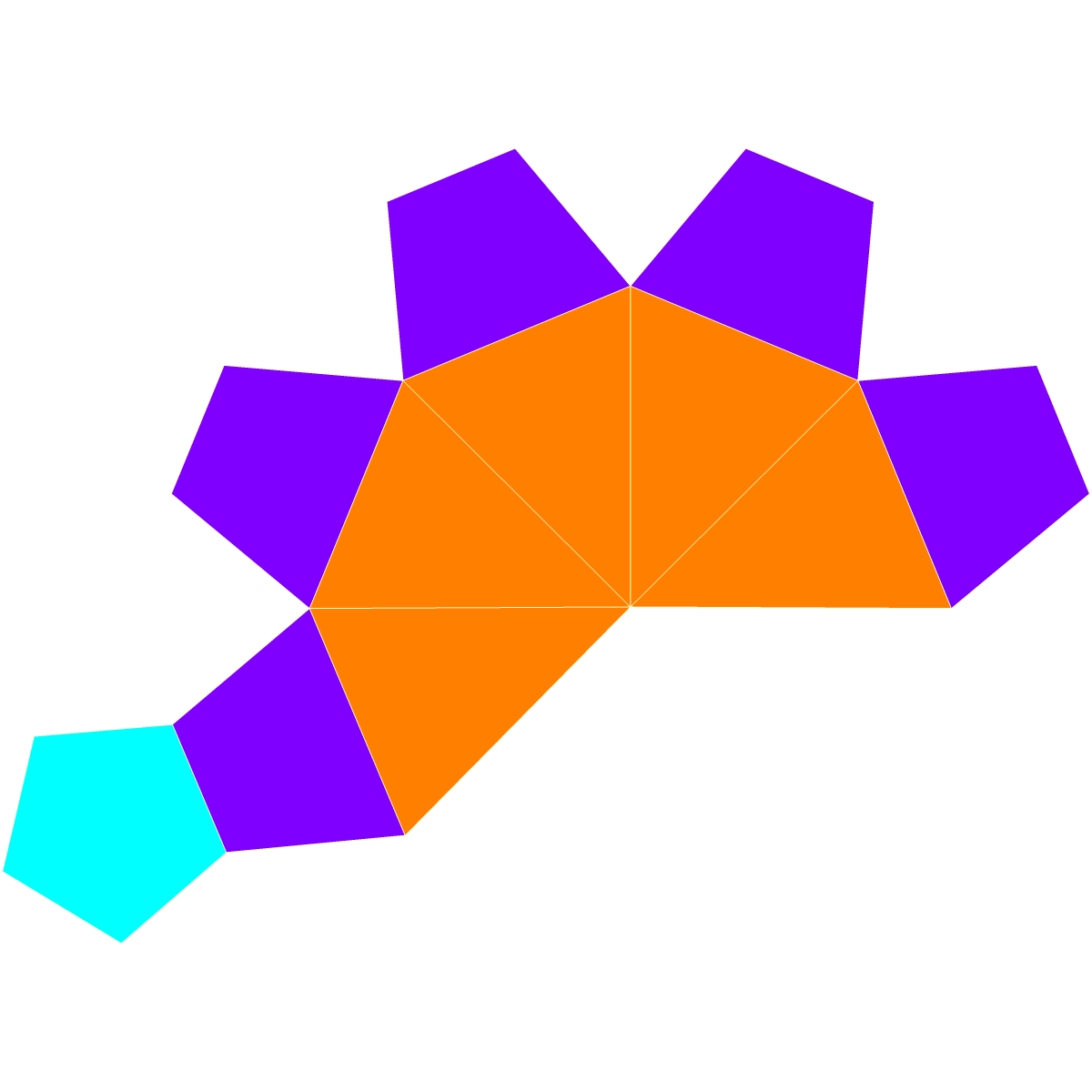
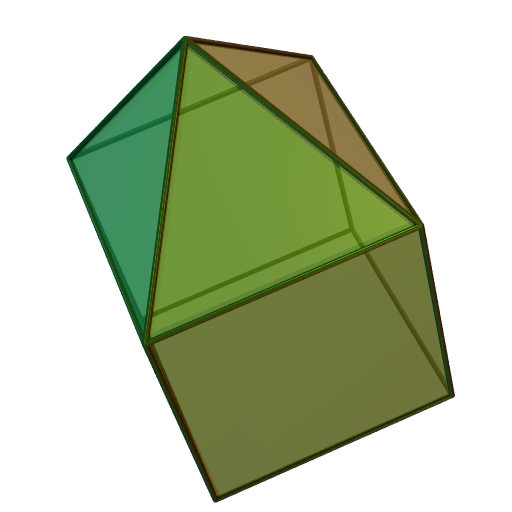
늘린 오각뿔은 11개의 면, 20개의 모서리, 11개의 꼭짓점을 가지는 다면체이다. 모든 면이 정다각형이고 변의 길이가 L일 때, 높이, 겉넓이, 부피를 구할 수 있다. 늘린 오각뿔의 쌍대 다면체는 11개의 면으로 이루어져 있으며, 5개의 삼각형, 1개의 오각형, 5개의 사다리꼴로 구성된다. 정오각기둥의 한 밑면에 정오각뿔을 붙이면 늘린 오각뿔이 된다.

2. 공식

모든 면이 정다각형이고 변의 길이가 $L$ 일 때, 높이( $H$ ), 겉넓이( $A$ ), 부피( $V$ )를 구하는 공식은 다음과 같다:^[2]

: $H = L\cdot \left( 1 + \sqrt{\frac{5 - \sqrt{5}}{10}}\right) \approx L\cdot 1.525731112$

: $A = L^2 \cdot \frac{20 + 5\sqrt{3} + \sqrt{25 + 10\sqrt{5}}}{4} \approx L^2\cdot 8.88554091$

: $V = L^3 \cdot \left( \frac{5 + \sqrt{5} + 6\sqrt{25 + 10\sqrt{5}}}{24} \right) \approx L^3\cdot 2.021980233$

한 변의 길이를 $a$ 라고 할 때, 겉넓이와 부피는 다음과 같이 나타낼 수 있다.

겉넓이: $S=}\over{4}}}a^2$
부피: $V=}\over{24}}}a^3$

3. 성질

늘린 오각뿔은 11개의 면, 20개의 모서리, 11개의 꼭짓점을 가진다.^[2] 겉넓이와 부피는 다음과 같다.

겉넓이: 한 변의 길이를 $a$ 라고 하면, $S=\frac{20+5\sqrt{3}+\sqrt{25+10\sqrt{5}}}{4}a^2$
부피: 한 변의 길이를 $a$ 라고 하면, $V=\frac{5+\sqrt{5}+6\sqrt{25+10\sqrt{5}}}{24}a^3$

4. 쌍대 다면체

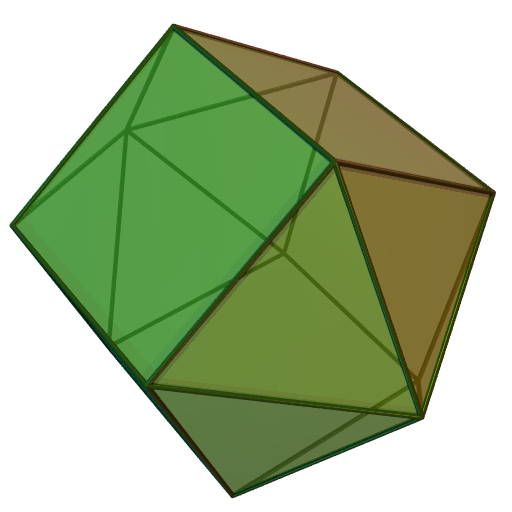
늘린 오각뿔의 쌍대 다면체는 11개의 면을 가지며, 5개의 삼각형, 1개의 오각형, 5개의 사다리꼴로 이루어져 있다. 이는 위상적으로 존슨의 다면체와 동일하다.

쌍대 늘린 오각뿔	전개도

5. 관련 다면체

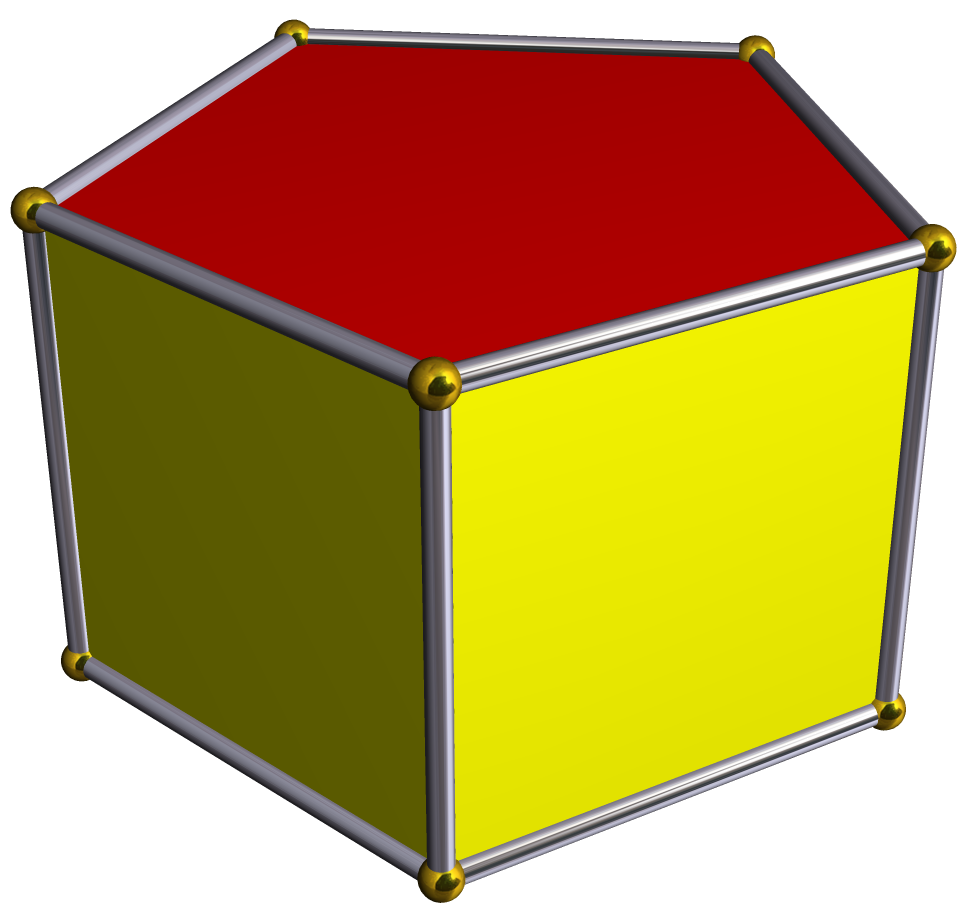
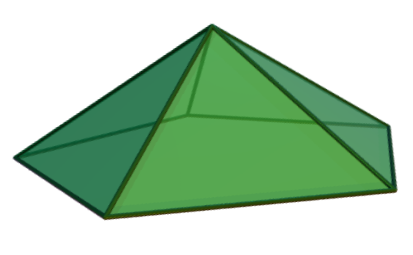
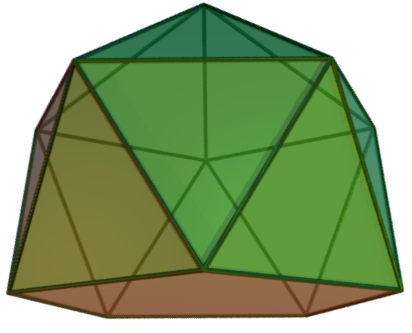
정오각기둥의 한 밑면에 정오각뿔을 붙이면 늘린 오각뿔이 된다. 정오각뿔의 밑면을 늘려 정오각기둥을 만들고, 그 위에 다시 정오각뿔을 붙이면 쌍오각뿔기둥이 된다. 정오각뿔의 밑면을 36° 비틀어 붙이면 정오각뿔반기둥이 된다. 정사각뿔기둥은 늘린 오각뿔에서 뿔의 모서리 수를 줄인 형태이고, 정삼각뿔기둥은 뿔의 모서리 수를 더 줄인 형태이다.

그림	이름	설명
	정오각기둥	정오각뿔을 제거
	정오각뿔	정오각기둥을 제거
	정사각뿔기둥	뿔의 모서리 수를 줄임
	정삼각뿔기둥	뿔의 모서리 수를 더 줄임
	쌍오각뿔기둥	정오각뿔을 추가
	정오각뿔반기둥	36° 비틀기

참조

_[1] 논문 Convex polyhedra with regular faces
_[2] 간행물 Area and volume of the Johnson solid J₉ https://www.problema[...] 2020-08-30
_[3] 논문 Convex polyhedra with regular faces

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com